Radioactivity and Nuclear Physics and its Medical Applications
118 Nuclear Decay and Conservation Laws
Learning Objectives
- Define and discuss nuclear decay.
- State the conservation laws.
- Explain parent and daughter nucleus.
- Calculate the energy emitted during nuclear decay.
Nuclear decay has provided an amazing window into the realm of the very small. Nuclear decay gave the first indication of the connection between mass and energy, and it revealed the existence of two of the four basic forces in nature. In this section, we explore the major modes of nuclear decay; and, like those who first explored them, we will discover evidence of previously unknown particles and conservation laws.
Some nuclides are stable, apparently living forever. Unstable nuclides decay (that is, they are radioactive), eventually producing a stable nuclide after many decays. We call the original nuclide the parent and its decay products the daughters. Some radioactive nuclides decay in a single step to a stable nucleus. For example, [latex]{}^{\text{60}}\text{Co}[/latex] is unstable and decays directly to [latex]{}^{\text{60}}\text{Ni}[/latex], which is stable. Others, such as [latex]{}^{\text{238}}\text{U}[/latex], decay to another unstable nuclide, resulting in a decay series in which each subsequent nuclide decays until a stable nuclide is finally produced. The decay series that starts from [latex]{}^{\text{238}}\text{U}[/latex] is of particular interest, since it produces the radioactive isotopes [latex]{}^{\text{226}}\text{Ra}[/latex] and [latex]{}^{\text{210}}\text{Po}[/latex], which the Curies first discovered (see Figure 118.1). Radon gas is also produced ([latex]{}^{\text{222}}\text{Rn}[/latex] in the series), an increasingly recognized naturally occurring hazard. Since radon is a noble gas, it emanates from materials, such as soil, containing even trace amounts of [latex]{}^{\text{238}}\text{U}[/latex] and can be inhaled. The decay of radon and its daughters produces internal damage. The [latex]{}^{\text{238}}\text{U}[/latex] decay series ends with [latex]{}^{\text{206}}\text{Pb}[/latex], a stable isotope of lead.
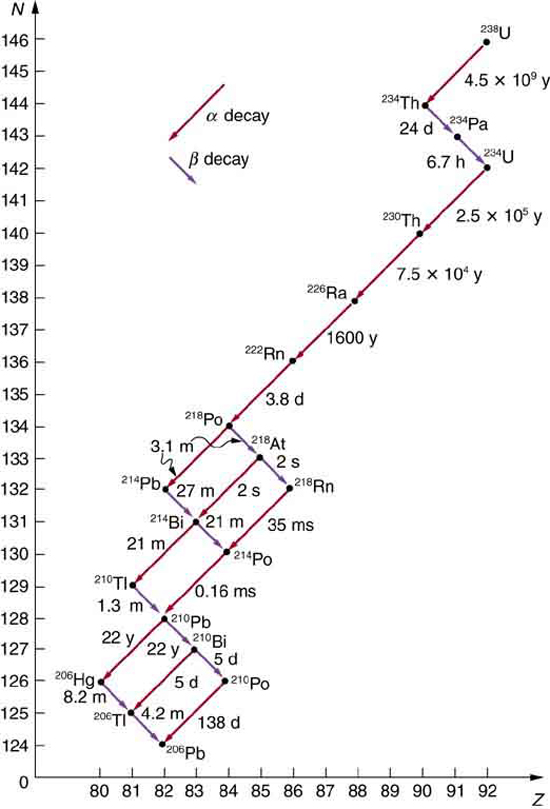
Note that the daughters of [latex]\alpha[/latex] decay shown in Figure 118.1 always have two fewer protons and two fewer neutrons than the parent. This seems reasonable, since we know that [latex]\alpha[/latex] decay is the emission of a [latex]{}^{4}\text{He}[/latex] nucleus, which has two protons and two neutrons. The daughters of [latex]\beta[/latex] decay have one less neutron and one more proton than their parent. Beta decay is a little more subtle, as we shall see. No [latex]\gamma[/latex] decays are shown in the figure, because they do not produce a daughter that differs from the parent.
Alpha Decay
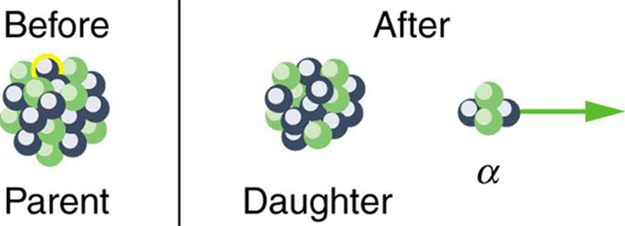
In alpha decay, a [latex]{}^{4}\text{He}[/latex] nucleus simply breaks away from the parent nucleus, leaving a daughter with two fewer protons and two fewer neutrons than the parent (see Figure 118.2). One example of [latex]\alpha[/latex] decay is shown in Figure 118.1 for [latex]{}^{\text{238}}\text{U}[/latex]. Another nuclide that undergoes [latex]\alpha[/latex] decay is [latex]{}^{\text{239}}\text{Pu}[/latex]. The decay equations for these two nuclides are
and
If you examine the periodic table of the elements, you will find that Th has [latex]Z=\text{90}[/latex], two fewer than U, which has [latex]Z=\text{92}[/latex]. Similarly, in the second decay equation, we see that U has two fewer protons than Pu, which has [latex]Z=\text{94}[/latex]. The general rule for [latex]\alpha[/latex] decay is best written in the format [latex]{}_{Z}^{A}{\text{X}}_{N}[/latex]. If a certain nuclide is known to [latex]\alpha[/latex] decay (generally this information must be looked up in a table of isotopes, such as in Appendix B), its [latex]\alpha[/latex] decay equation is
where Y is the nuclide that has two fewer protons than X, such as Th having two fewer than U. So if you were told that [latex]{}^{\text{239}}\text{Pu}[/latex] [latex]\alpha[/latex] decays and were asked to write the complete decay equation, you would first look up which element has two fewer protons (an atomic number two lower) and find that this is uranium. Then since four nucleons have broken away from the original 239, its atomic mass would be 235.
It is instructive to examine conservation laws related to [latex]\alpha[/latex] decay. You can see from the equation [latex]{}_{Z}^{A}{\text{X}}_{N}\to {}_{Z-2}^{A-4}{\text{Y}}_{N-2}+{}_{2}^{4}{\text{He}}_{2}[/latex] that total charge is conserved. Linear and angular momentum are conserved, too. Although conserved angular momentum is not of great consequence in this type of decay, conservation of linear momentum has interesting consequences. If the nucleus is at rest when it decays, its momentum is zero. In that case, the fragments must fly in opposite directions with equal-magnitude momenta so that total momentum remains zero. This results in the [latex]\alpha[/latex] particle carrying away most of the energy, as a bullet from a heavy rifle carries away most of the energy of the powder burned to shoot it. Total mass–energy is also conserved: the energy produced in the decay comes from conversion of a fraction of the original mass. As discussed in Atomic Physics, the general relationship is
Here, [latex]E[/latex] is the nuclear reaction energy (the reaction can be nuclear decay or any other reaction), and [latex]\Delta m[/latex] is the difference in mass between initial and final products. When the final products have less total mass, [latex]\Delta m[/latex] is positive, and the reaction releases energy (is exothermic). When the products have greater total mass, the reaction is endothermic ([latex]\Delta m[/latex] is negative) and must be induced with an energy input. For [latex]\alpha[/latex] decay to be spontaneous, the decay products must have smaller mass than the parent.
Example 118.1: Alpha Decay Energy Found from Nuclear Masses
Find the energy emitted in the [latex]\alpha[/latex] decay of [latex]{}^{\text{239}}\text{Pu}[/latex].
Strategy
Nuclear reaction energy, such as released in α decay, can be found using the equation [latex]E=\left(\Delta m\right){c}^{2}[/latex]. We must first find [latex]\Delta m[/latex], the difference in mass between the parent nucleus and the products of the decay. This is easily done using masses given in Appendix A.
Solution
The decay equation was given earlier for [latex]{}^{\text{239}}\text{Pu}[/latex] ; it is
Thus the pertinent masses are those of [latex]{}^{\text{239}}\text{Pu}[/latex], [latex]{}^{\text{235}}\text{U}[/latex], and the [latex]\alpha[/latex] particle or [latex]{}^{4}\text{He}[/latex], all of which are listed in Appendix A. The initial mass was [latex]m{\left(}^{\text{239}}\text{Pu}\right)=\text{239}\text{.}\text{052157 u}[/latex]. The final mass is the sum [latex]m{\left(}^{\text{235}}\text{U}\right)\text{+}m{\left(}^{4}\text{He}\right)\text{= 235}\text{.}\text{043924 u + 4.002602 u = 239.046526 u}[/latex]. Thus,
Now we can find [latex]E[/latex] by entering [latex]\Delta m[/latex] into the equation:
We know [latex]\text{1 u}=\text{931.5 MeV/}{c}^{2}[/latex], and so
Discussion
The energy released in this [latex]\alpha[/latex] decay is in the [latex]\text{MeV}[/latex] range, about [latex]{\text{10}}^{6}[/latex] times as great as typical chemical reaction energies, consistent with many previous discussions. Most of this energy becomes kinetic energy of the [latex]\alpha[/latex] particle (or [latex]{}^{4}\text{He}[/latex] nucleus), which moves away at high speed. The energy carried away by the recoil of the [latex]{}^{\text{235}}\text{U}[/latex] nucleus is much smaller in order to conserve momentum. The [latex]{}^{\text{235}}\text{U}[/latex] nucleus can be left in an excited state to later emit photons ([latex]\gamma[/latex] rays). This decay is spontaneous and releases energy, because the products have less mass than the parent nucleus. The question of why the products have less mass will be discussed in Binding Energy. Note that the masses given in Appendix A are atomic masses of neutral atoms, including their electrons. The mass of the electrons is the same before and after [latex]\alpha[/latex] decay, and so their masses subtract out when finding [latex]\Delta m[/latex]. In this case, there are 94 electrons before and after the decay.
Beta Decay
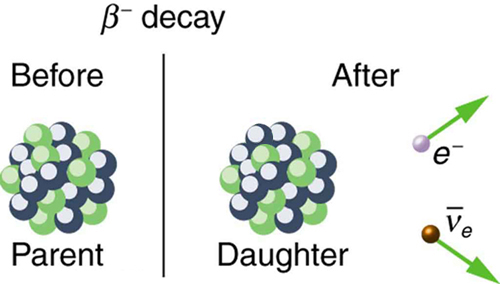
There are actually three types of beta decay. The first discovered was “ordinary” beta decay and is called [latex]{\beta }^{-}[/latex] decay or electron emission. The symbol [latex]{\beta }^{-}[/latex] represents an electron emitted in nuclear beta decay. Cobalt-60 is a nuclide that [latex]{\beta }^{-}[/latex] decays in the following manner:
The neutrino is a particle emitted in beta decay that was unanticipated and is of fundamental importance. The neutrino was not even proposed in theory until more than 20 years after beta decay was known to involve electron emissions. Neutrinos are so difficult to detect that the first direct evidence of them was not obtained until 1953. Neutrinos are nearly massless, have no charge, and do not interact with nucleons via the strong nuclear force. Traveling approximately at the speed of light, they have little time to affect any nucleus they encounter. This is, owing to the fact that they have no charge (and they are not EM waves), they do not interact through the EM force. They do interact via the relatively weak and very short range weak nuclear force. Consequently, neutrinos escape almost any detector and penetrate almost any shielding. However, neutrinos do carry energy, angular momentum (they are fermions with half-integral spin), and linear momentum away from a beta decay. When accurate measurements of beta decay were made, it became apparent that energy, angular momentum, and linear momentum were not accounted for by the daughter nucleus and electron alone. Either a previously unsuspected particle was carrying them away, or three conservation laws were being violated. Wolfgang Pauli made a formal proposal for the existence of neutrinos in 1930. The Italian-born American physicist Enrico Fermi (1901–1954) gave neutrinos their name, meaning little neutral ones, when he developed a sophisticated theory of beta decay (see Figure 118.3(a)). Part of Fermi’s theory was the identification of the weak nuclear force as being distinct from the strong nuclear force and in fact responsible for beta decay. Chinese-born physicist Chien-Shiung Wu (see Figure 118.3(b)), who had developed a number of processes critical to the Manhattan Project and related research, set out to investigate Fermi’s theory and some experiments whose failures had cast the theory in doubt. She first identified a number of flaws in her contemporaries’ methods and materials, and then designed an experimental method that would avoid the same errors. Wu verified Fermi’s theory and went on to establish the core principles of beta decay, which would become critical to further work in nuclear physics.
The neutrino also reveals a new conservation law. There are various families of particles, one of which is the electron family. We propose that the number of members of the electron family is constant in any process or any closed system. In our example of beta decay, there are no members of the electron family present before the decay, but after, there is an electron and a neutrino. So electrons are given an electron family number of [latex]+1[/latex]. The neutrino in [latex]{\beta }^{-}[/latex] decay is an electron’s antineutrino, given the symbol [latex]{\overline{\nu }}_{e}[/latex], where [latex]\nu[/latex] is the Greek letter nu, and the subscript e means this neutrino is related to the electron. The bar indicates this is a particle of antimatter. (All particles have antimatter counterparts that are nearly identical except that they have the opposite charge. Antimatter is almost entirely absent on Earth, but it is found in nuclear decay and other nuclear and particle reactions as well as in outer space.) The electron’s antineutrino [latex]{\overline{\nu }}_{e}[/latex], being antimatter, has an electron family number of [latex]–1[/latex]. The total is zero, before and after the decay. The new conservation law, obeyed in all circumstances, states that the total electron family number is constant. An electron cannot be created without also creating an antimatter family member. This law is analogous to the conservation of charge in a situation where total charge is originally zero, and equal amounts of positive and negative charge must be created in a reaction to keep the total zero.
If a nuclide [latex]{}_{Z}^{A}{X}_{N}[/latex] is known to [latex]{\beta }^{-}[/latex] decay, then its [latex]{\beta }^{-}[/latex] decay equation is
where Y is the nuclide having one more proton than X (see Figure 118.4). So if you know that a certain nuclide [latex]{\beta }^{-}[/latex] decays, you can find the daughter nucleus by first looking up
[latex]Z[/latex] for the parent and then determining which element has atomic number [latex]Z+1[/latex]. In the example of the [latex]{\beta }^{-}[/latex] decay of [latex]{}^{\text{60}}\text{Co}[/latex] given earlier, we see that [latex]Z=\text{27}[/latex] for Co and [latex]Z=\text{28}[/latex] is Ni. It is as if one of the neutrons in the parent nucleus decays into a proton, electron, and neutrino. In fact, neutrons outside of nuclei do just that—they live only an average of a few minutes and [latex]{\beta }^{-}[/latex] decay in the following manner:
We see that charge is conserved in [latex]{\beta }^{-}[/latex] decay, since the total charge is [latex]Z[/latex] before and after the decay. For example, in [latex]{}^{\text{60}}\text{Co}[/latex] decay, total charge is 27 before decay, since cobalt has [latex]Z=\text{27}[/latex]. After decay, the daughter nucleus is Ni, which has [latex]Z=\text{28}[/latex], and there is an electron, so that the total charge is also [latex]28 + \left(–1\right)[/latex] or 27. Angular momentum is conserved, but not obviously (you have to examine the spins and angular momenta of the final products in detail to verify this). Linear momentum is also conserved, again imparting most of the decay energy to the electron and the antineutrino, since they are of low and zero mass, respectively. Another new conservation law is obeyed here and elsewhere in nature. The total number of nucleons [latex]A[/latex] is conserved. In [latex]{}^{\text{60}}\text{Co}[/latex] decay, for example, there are 60 nucleons before and after the decay. Note that total [latex]A[/latex] is also conserved in [latex]\alpha[/latex] decay. Also note that the total number of protons changes, as does the total number of neutrons, so that total [latex]Z[/latex] and total [latex]N[/latex] are not conserved in [latex]{\beta }^{-}[/latex] decay, as they are in [latex]\alpha[/latex] decay. Energy released in [latex]{\beta }^{-}[/latex] decay can be calculated given the masses of the parent and products.
Example 118.2: [latex]{\beta }^{-}[/latex] Decay Energy from Masses
Find the energy emitted in the [latex]{\beta }^{-}[/latex] decay of [latex]{}^{\text{60}}\text{Co}[/latex].
Strategy and Concept
As in the preceding example, we must first find [latex]\Delta m[/latex], the difference in mass between the parent nucleus and the products of the decay, using masses given in Appendix A. Then the emitted energy is calculated as before, using [latex]E=\left(\Delta m\right){c}^{2}[/latex]. The initial mass is just that of the parent nucleus, and the final mass is that of the daughter nucleus and the electron created in the decay. The neutrino is massless, or nearly so. However, since the masses given in Appendix A are for neutral atoms, the daughter nucleus has one more electron than the parent, and so the extra electron mass that corresponds to the [latex]{\beta }^{–}[/latex] is included in the atomic mass of Ni. Thus,
Solution
The [latex]{\beta }^{-}[/latex] decay equation for [latex]{}^{\text{60}}\text{Co}[/latex] is
As noticed,
Entering the masses found in Appendix A gives
Thus,
Using [latex]1 u=931.5 MeV/{c}^{2}[/latex], we obtain
Discussion and Implications
Perhaps the most difficult thing about this example is convincing yourself that the [latex]{\beta }^{-}[/latex] mass is included in the atomic mass of [latex]{}^{\text{60}}\text{Ni}[/latex]. Beyond that are other implications. Again the decay energy is in the MeV range. This energy is shared by all of the products of the decay. In many [latex]{}^{\text{60}}\text{Co}[/latex] decays, the daughter nucleus [latex]{}^{\text{60}}\text{Ni}[/latex] is left in an excited state and emits photons (
[latex]\gamma[/latex] rays). Most of the remaining energy goes to the electron and neutrino, since the recoil kinetic energy of the daughter nucleus is small. One final note: the electron emitted in [latex]{\beta }^{-}[/latex] decay is created in the nucleus at the time of decay.
The second type of beta decay is less common than the first. It is [latex]{\beta }^{+}[/latex]decay. Certain nuclides decay by the emission of a positive electron. This is antielectron or positron decay (see Figure 118.5).
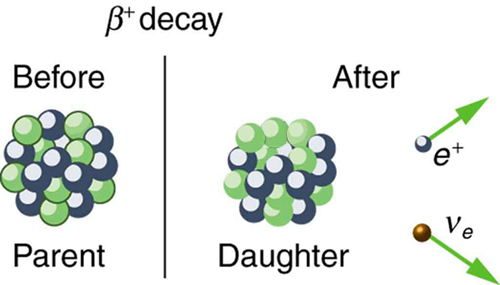
The antielectron is often represented by the symbol [latex]{e}^{+}[/latex], but in beta decay it is written as [latex]{\beta }^{+}[/latex] to indicate the antielectron was emitted in a nuclear decay. Antielectrons are the antimatter counterpart to electrons, being nearly identical, having the same mass, spin, and so on, but having a positive charge and an electron family number of [latex]–1[/latex]. When a positron encounters an electron, there is a mutual annihilation in which all the mass of the antielectron-electron pair is converted into pure photon energy. (The reaction, [latex]{e}^{+}+{e}^{-}\to \gamma +\gamma[/latex], conserves electron family number as well as all other conserved quantities.) If a nuclide [latex]{}_{Z}^{A}{X}_{N}[/latex] is known to [latex]{\beta }^{+}[/latex] decay, then its [latex]{\beta }^{+}[/latex]decay equation is
where Y is the nuclide having one less proton than X (to conserve charge) and [latex]{\nu }_{e}[/latex] is the symbol for the electron’s neutrino, which has an electron family number of [latex]+1[/latex]. Since an antimatter member of the electron family (the [latex]{\beta }^{+}[/latex]) is created in the decay, a matter member of the family (here the [latex]{\nu }_{e}[/latex]) must also be created. Given, for example, that [latex]{}^{\text{22}}\text{Na}[/latex] [latex]{\beta }^{+}[/latex] decays, you can write its full decay equation by first finding that [latex]Z=\text{11}[/latex] for [latex]{}^{\text{22}}\text{Na}[/latex], so that the daughter nuclide will have [latex]Z=\text{10}[/latex], the atomic number for neon. Thus the [latex]{\beta }^{+}[/latex] decay equation for [latex]{}^{\text{22}}\text{Na}[/latex] is
In [latex]{\beta }^{+}[/latex] decay, it is as if one of the protons in the parent nucleus decays into a neutron, a positron, and a neutrino. Protons do not do this outside of the nucleus, and so the decay is due to the complexities of the nuclear force. Note again that the total number of nucleons is constant in this and any other reaction. To find the energy emitted in [latex]{\beta }^{+}[/latex] decay, you must again count the number of electrons in the neutral atoms, since atomic masses are used. The daughter has one less electron than the parent, and one electron mass is created in the decay. Thus, in [latex]{\beta }^{+}[/latex] decay,
since we use the masses of neutral atoms.
Electron capture is the third type of beta decay. Here, a nucleus captures an inner-shell electron and undergoes a nuclear reaction that has the same effect as [latex]{\beta }^{+}[/latex] decay. Electron capture is sometimes denoted by the letters EC. We know that electrons cannot reside in the nucleus, but this is a nuclear reaction that consumes the electron and occurs spontaneously only when the products have less mass than the parent plus the electron. If a nuclide [latex]{}_{Z}^{A}{X}_{N}[/latex] is known to undergo electron capture, then its electron capture equation is
Any nuclide that can [latex]{\beta }^{+}[/latex] decay can also undergo electron capture (and often does both). The same conservation laws are obeyed for EC as for [latex]{\beta }^{+}[/latex] decay. It is good practice to confirm these for yourself.
All forms of beta decay occur because the parent nuclide is unstable and lies outside the region of stability in the chart of nuclides. Those nuclides that have relatively more neutrons than those in the region of stability will [latex]{\beta }^{-}[/latex] decay to produce a daughter with fewer neutrons, producing a daughter nearer the region of stability. Similarly, those nuclides having relatively more protons than those in the region of stability will [latex]{\beta }^{-}[/latex] decay or undergo electron capture to produce a daughter with fewer protons, nearer the region of stability.
Gamma Decay
Gamma decay is the simplest form of nuclear decay—it is the emission of energetic photons by nuclei left in an excited state by some earlier process. Protons and neutrons in an excited nucleus are in higher orbitals, and they fall to lower levels by photon emission (analogous to electrons in excited atoms). Nuclear excited states have lifetimes typically of only about [latex]{\text{10}}^{-\text{14}}[/latex] s, an indication of the great strength of the forces pulling the nucleons to lower states. The [latex]\gamma[/latex] decay equation is simply
where the asterisk indicates the nucleus is in an excited state. There may be one or more [latex]\gamma[/latex] s emitted, depending on how the nuclide de-excites. In radioactive decay, [latex]\gamma[/latex] emission is common and is preceded by [latex]\gamma[/latex] or [latex]\beta[/latex] decay. For example, when [latex]{}^{\text{60}}\text{Co}[/latex] [latex]{\beta }^{-}[/latex] decays, it most often leaves the daughter nucleus in an excited state, written [latex]{}^{\text{60}}\text{Ni*}[/latex]. Then the nickel nucleus quickly [latex]\gamma[/latex] decays by the emission of two penetrating [latex]\gamma[/latex] s:
These are called cobalt [latex]\gamma[/latex] rays, although they come from nickel—they are used for cancer therapy, for example. It is again constructive to verify the conservation laws for gamma decay. Finally, since [latex]\gamma[/latex] decay does not change the nuclide to another species, it is not prominently featured in charts of decay series, such as that in Figure 118.1.
There are other types of nuclear decay, but they occur less commonly than [latex]\alpha[/latex],
[latex]\beta[/latex], and [latex]\gamma[/latex] decay. Spontaneous fission is the most important of the other forms of nuclear decay because of its applications in nuclear power and weapons. It is covered in the next chapter.
Section Summary
- When a parent nucleus decays, it produces a daughter nucleus following rules and conservation laws. There are three major types of nuclear decay, called alpha [latex]\left(\alpha \right),[/latex] beta [latex]\left(\beta \right),[/latex] and gamma [latex]\left(\gamma \right)[/latex]. The [latex]\alpha[/latex] decay equation is
[latex]{}_{Z}^{A}{X}_{N}\to {}_{Z-2}^{A-4}{\text{Y}}_{N-2}+{}_{2}^{4}{\text{He}}_{2}.[/latex]
- Nuclear decay releases an amount of energy [latex]E[/latex] related to the mass destroyed [latex]\Delta m[/latex] by
[latex]E=\left(\Delta m\right){c}^{2}.[/latex]
- There are three forms of beta decay. The [latex]{\beta }^{-}[/latex]decay equation is
[latex]{}_{Z}^{A}{X}_{N}\to {}_{Z+1}^{A}{\text{Y}}_{N-1}+{\beta }^{-}+{\overline{\nu }}_{e}.[/latex]
- The [latex]{\beta }^{+}[/latex] decay equation is
[latex]{}_{Z}^{A}{X}_{N}\to {}_{Z-1}^{A}{\text{Y}}_{N+1}+{\beta }^{+}+{\nu }_{e}.[/latex]
- The electron capture equation is
[latex]{}_{Z}^{A}{X}_{N}+{e}^{-}\to {}_{Z-1}^{A}{\text{Y}}_{N+1}+{\nu }_{e}.[/latex]
- [latex]{\beta }^{-}[/latex] is an electron, [latex]{\beta }^{+}[/latex] is an antielectron or positron, [latex]{\nu }_{e}[/latex] represents an electron’s neutrino, and [latex]{\overline{\nu }}_{e}[/latex] is an electron’s antineutrino. In addition to all previously known conservation laws, two new ones arise— conservation of electron family number and conservation of the total number of nucleons. The [latex]\gamma[/latex] decay equation is
[latex]{}_{Z}{}^{A}\text{}{\text{X}}_{N}^{*}\to {}_{Z}{}^{A}\text{}{\text{X}}_{N}+{\gamma }_{1}+{\gamma }_{2}+\cdots[/latex]
[latex]\gamma[/latex] is a high-energy photon originating in a nucleus.
Conceptual Questions
- Star Trek fans have often heard the term “antimatter drive.” Describe how you could use a magnetic field to trap antimatter, such as produced by nuclear decay, and later combine it with matter to produce energy. Be specific about the type of antimatter, the need for vacuum storage, and the fraction of matter converted into energy.
- What conservation law requires an electron’s neutrino to be produced in electron capture? Note that the electron no longer exists after it is captured by the nucleus.
- Neutrinos are experimentally determined to have an extremely small mass. Huge numbers of neutrinos are created in a supernova at the same time as massive amounts of light are first produced. When the 1987A supernova occurred in the Large Magellanic Cloud, visible primarily in the Southern Hemisphere and some 100,000 light-years away from Earth, neutrinos from the explosion were observed at about the same time as the light from the blast. How could the relative arrival times of neutrinos and light be used to place limits on the mass of neutrinos?
- What do the three types of beta decay have in common that is distinctly different from alpha decay?
Problems & Exercises
In the following eight problems, write the complete decay equation for the given nuclide in the complete [latex]{}_{Z}^{A}{X}_{N}[/latex] notation. Refer to the periodic table for values of [latex]Z[/latex].
- [latex]{\beta }^{-}[/latex] decay of [latex]{}^{3}\text{H}[/latex] (tritium), a manufactured isotope of hydrogen used in some digital watch displays, and manufactured primarily for use in hydrogen bombs.
- [latex]{\beta }^{-}[/latex] decay of [latex]{}^{\text{40}}K[/latex], a naturally occurring rare isotope of potassium responsible for some of our exposure to background radiation.
- [latex]{\beta }^{+}[/latex] decay of [latex]{}^{\text{52}}\text{Fe}[/latex].
- Electron capture by [latex]{}^{7}\text{Be}[/latex].
- Electron capture by [latex]{}^{\text{106}}\text{In}[/latex].
- [latex]\alpha[/latex] decay of [latex]{}^{\text{210}}\text{Po}[/latex], the isotope of polonium in the decay series of [latex]{}^{\text{238}}\text{U}[/latex] that was discovered by the Curies. A favorite isotope in physics labs, since it has a short half-life and decays to a stable nuclide.
- [latex]\alpha[/latex] decay of [latex]{}^{\text{226}}\text{Ra}[/latex], another isotope in the decay series of [latex]{}^{\text{238}}\text{U}[/latex], first recognized as a new element by the Curies. Poses special problems because its daughter is a radioactive noble gas.
- In the following four problems, identify the parent nuclide and write the complete decay equation in the [latex]{}_{Z}^{A}{X}_{N}[/latex] notation. Refer to the periodic table for values of [latex]Z[/latex]. [latex]{\beta }^{-}[/latex] decay producing [latex]{}^{\text{137}}\text{Ba}[/latex]. The parent nuclide is a major waste product of reactors and has chemistry similar to potassium and sodium, resulting in its concentration in your cells if ingested.
- [latex]{\beta }^{-}[/latex] decay producing [latex]{}^{\text{90}}\text{Y}[/latex]. The parent nuclide is a major waste product of reactors and has chemistry similar to calcium, so that it is concentrated in bones if ingested ([latex]{}^{\text{90}}\text{Y}[/latex] is also radioactive.)
- [latex]\alpha[/latex] decay producing [latex]{}^{\text{228}}\text{Ra}[/latex]. The parent nuclide is nearly 100% of the natural element and is found in gas lantern mantles and in metal alloys used in jets ([latex]{}^{\text{228}}\text{Ra}[/latex] is also radioactive).
- [latex]\alpha[/latex] decay producing [latex]{}^{\text{208}}\text{Pb}[/latex]. The parent nuclide is in the decay series produced by [latex]{}^{\text{232}}\text{Th}[/latex], the only naturally occurring isotope of thorium.
- When an electron and positron annihilate, both their masses are destroyed, creating two equal energy photons to preserve momentum. (a) Confirm that the annihilation equation [latex]{e}^{+}+{e}^{-}\to \gamma +\gamma[/latex] conserves charge, electron family number, and total number of nucleons. To do this, identify the values of each before and after the annihilation. (b) Find the energy of each [latex]\gamma[/latex] ray, assuming the electron and positron are initially nearly at rest. (c) Explain why the two [latex]\gamma[/latex] rays travel in exactly opposite directions if the center of mass of the electron-positron system is initially at rest.
- Confirm that charge, electron family number, and the total number of nucleons are all conserved by the rule for [latex]\alpha[/latex] decay given in the equation [latex]{}_{Z}^{A}{X}_{N}\to {}_{Z-2}^{A-4}{\text{Y}}_{N-2}+{}_{2}^{4}{\text{He}}_{2}[/latex]. To do this, identify the values of each before and after the decay.
- Confirm that charge, electron family number, and the total number of nucleons are all conserved by the rule for [latex]{\beta }^{-}[/latex] decay given in the equation [latex]{}_{Z}^{A}{X}_{N}\to {}_{Z+1}^{A}{\text{Y}}_{N-1}+{\beta }^{-}+{\overline{\nu }}_{e}[/latex]. To do this, identify the values of each before and after the decay.
- Confirm that charge, electron family number, and the total number of nucleons are all conserved by the rule for [latex]{\beta }^{-}[/latex] decay given in the equation [latex]{}_{Z}^{A}{X}_{N}\to {}_{Z-1}^{A}{\text{Y}}_{N-1}+{\beta }^{-}+{\nu }_{e}[/latex]. To do this, identify the values of each before and after the decay.
- Confirm that charge, electron family number, and the total number of nucleons are all conserved by the rule for electron capture given in the equation [latex]{}_{Z}^{A}{X}_{N}+{e}^{-}\to {}_{Z-1}^{A}{\text{Y}}_{N+1}+{\nu }_{e}[/latex]. To do this, identify the values of each before and after the capture.
- A rare decay mode has been observed in which [latex]{}^{\text{222}}\text{Ra}[/latex] emits a [latex]{}^{\text{14}}C[/latex] nucleus. (a) The decay equation is[latex]{}^{\text{222}}\text{Ra}{\to }^{A}{\text{X+}}^{\text{14}}\text{C}[/latex]. Identify the nuclide [latex]{}^{A}X[/latex]. (b) Find the energy emitted in the decay. The mass of [latex]{}^{\text{222}}\text{Ra}[/latex] is 222.015353 u. (a) Write the complete [latex]\alpha[/latex] decay equation for [latex]{}^{\text{226}}\text{Ra}[/latex]. (b) Find the energy released in the decay.
- (a) Write the complete [latex]\alpha[/latex] decay equation for [latex]{}^{\text{249}}\text{Cf}[/latex]. (b) Find the energy released in the decay.
- (a) Write the complete [latex]{\beta }^{-}[/latex] decay equation for the neutron. (b) Find the energy released in the decay.
- (a) Write the complete [latex]{\beta }^{-}[/latex] decay equation for [latex]{}^{\text{90}}\text{Sr}[/latex], a major waste product of nuclear reactors. (b) Find the energy released in the decay.
- Calculate the energy released in the [latex]{\beta }^{+}[/latex] decay of [latex]{}^{\text{22}}\text{Na}[/latex], the equation for which is given in the text. The masses of [latex]{}^{\text{22}}\text{Na}[/latex] and [latex]{}^{\text{22}}\text{Ne}[/latex] are 21.994434 and 21.991383 u, respectively.
- (a) Write the complete [latex]{\beta }^{+}[/latex] decay equation for [latex]{}^{\text{11}}\text{C}[/latex]. (b) Calculate the energy released in the decay. The masses of [latex]{}^{\text{11}}\text{C}[/latex] and [latex]{}^{\text{11}}\text{B}[/latex] are 11.011433 and 11.009305 u, respectively.
- (a) Calculate the energy released in the [latex]\alpha[/latex] decay of [latex]{}^{\text{238}}\text{U}[/latex]. (b) What fraction of the mass of a single [latex]{}^{\text{238}}\text{U}[/latex] is destroyed in the decay? The mass of [latex]{}^{\text{234}}\text{Th}[/latex] is 234.043593 u. (c) Although the fractional mass loss is large for a single nucleus, it is difficult to observe for an entire macroscopic sample of uranium. Why is this?
- (a) Write the complete reaction equation for electron capture by [latex]{}^{7}\text{Be.}[/latex] (b) Calculate the energy released.
- (a) Write the complete reaction equation for electron capture by [latex]{}^{\text{15}}\text{O}[/latex]. (b) Calculate the energy released
Glossary
- parent
- the original state of nucleus before decay
- daughter
- the nucleus obtained when parent nucleus decays and produces another nucleus following the rules and the conservation laws
- positron
- the particle that results from positive beta decay; also known as an antielectron
- decay
- the process by which an atomic nucleus of an unstable atom loses mass and energy by emitting ionizing particles
- alpha decay
- type of radioactive decay in which an atomic nucleus emits an alpha particle
- beta decay
- type of radioactive decay in which an atomic nucleus emits a beta particle
- gamma decay
- type of radioactive decay in which an atomic nucleus emits a gamma particle
- decay equation
- the equation to find out how much of a radioactive material is left after a given period of time
- nuclear reaction energy
- the energy created in a nuclear reaction
- neutrino
- an electrically neutral, weakly interacting elementary subatomic particle
- electron’s antineutrino
- antiparticle of electron’s neutrino
- positron decay
- type of beta decay in which a proton is converted to a neutron, releasing a positron and a neutrino
- antielectron
- another term for positron
- decay series
- process whereby subsequent nuclides decay until a stable nuclide is produced
- electron’s neutrino
- a subatomic elementary particle which has no net electric charge
- antimatter
- composed of antiparticles
- electron capture
- the process in which a proton-rich nuclide absorbs an inner atomic electron and simultaneously emits a neutrino
- electron capture equation
- equation representing the electron capture

