Magnetic Field Created by a Long Straight Current-Carrying Wire: Right Hand Rule 2

If we now generalize and instead of focusing on a single charge we study the effect for a line of current. As noted before, one way to explore the direction of a magnetic field is with compasses, as shown for a long straight current-carrying wire in (Figure). Hall probes can determine the magnitude of the field. The field around a long straight wire is found to be in circular loops. The right hand rule 2 (RHR-2) emerges from this exploration and is valid for any current segment—point the thumb in the direction of the current, and the fingers curl in the direction of the magnetic field loops created by it.

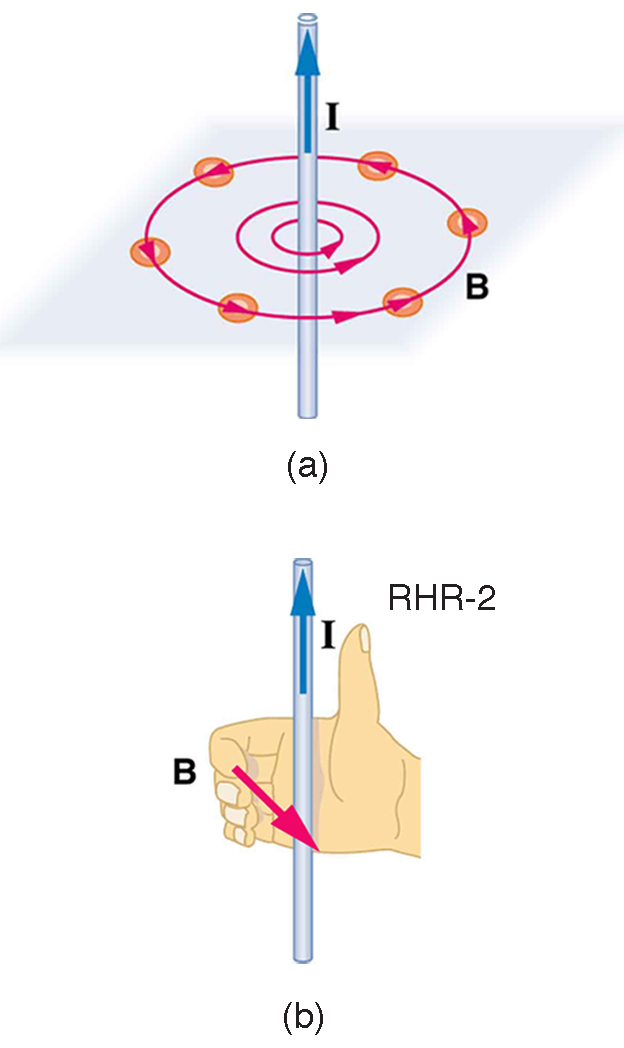
The magnetic field strength (magnitude) produced by a long straight current-carrying wire is found by experiment to be

where [latex]I[/latex] is the current, [latex]r[/latex] is the shortest distance to the wire, and the constant [latex]{\mu }_{0}=4\pi \phantom{\rule{0.15em}{0ex}}×\phantom{\rule{0.15em}{0ex}}{\text{10}}^{-7}\phantom{\rule{0.25em}{0ex}}T\cdot \text{m/A}[/latex] is the permeability of free space.
[latex]{\mu }_{0}[/latex] is one of the basic constants in nature. We will see later that [latex]{\mu }_{0}[/latex] is related to the speed of light.) Since the wire is very long, the magnitude of the field depends only on distance from the wire [latex]r[/latex], not on position along the wire.

Ampere’s Law and Others

The magnetic field of a long straight wire has more implications than you might at first suspect. Each segment of current produces a magnetic field like that of a long straight wire, and the total field of any shape current is the vector sum of the fields due to each segment. The formal statement of the direction and magnitude of the field due to each segment is called the Biot-Savart law. Integral calculus is needed to sum the field for an arbitrary shape current. This results in a more complete law, called Ampere’s law, which relates magnetic field and current in a general way. Ampere’s law in turn is a part of Maxwell’s equations, which give a complete theory of all electromagnetic phenomena. Considerations of how Maxwell’s equations appear to different observers led to the modern theory of relativity, and the realization that electric and magnetic fields are different manifestations of the same thing. Most of this is beyond the scope of this text in both mathematical level, requiring calculus, and in the amount of space that can be devoted to it. But for the interested student, and particularly for those who continue in physics, engineering, or similar pursuits, delving into these matters further will reveal descriptions of nature that are elegant as well as profound. In this text, we shall keep the general features in mind, such as RHR-2 and the rules for magnetic field lines listed in Magnetic Fields and Magnetic Field Lines, while concentrating on the fields created in certain important situations.

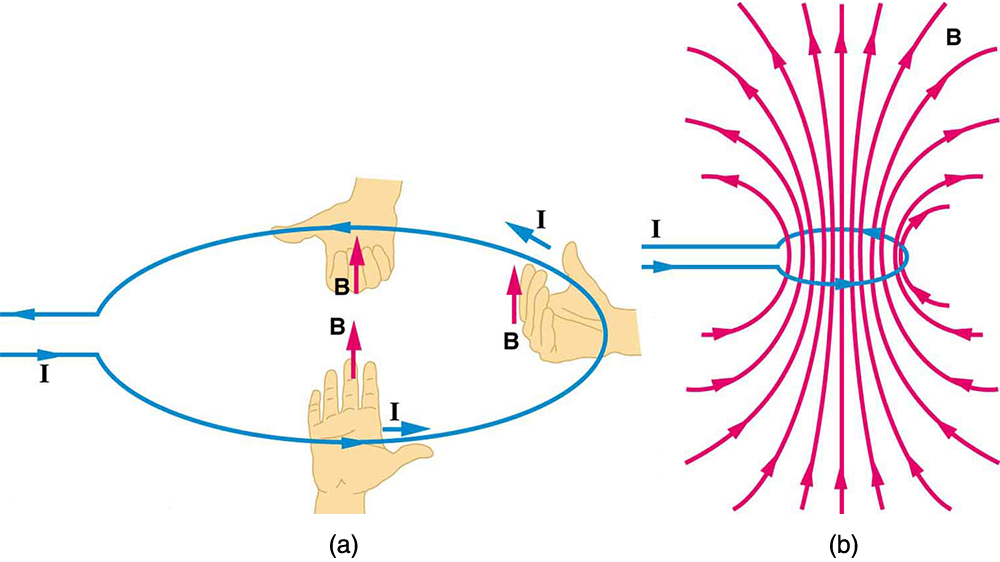
Magnetic Field Produced by a Current-Carrying Circular Loop

The magnetic field near a current-carrying loop of wire is shown in (Figure). Both the direction and the magnitude of the magnetic field produced by a current-carrying loop are complex. RHR-2 can be used to give the direction of the field near the loop, but mapping with compasses and the rules about field lines given in Magnetic Fields and Magnetic Field Lines are needed for more detail. There is a simple formula for the magnetic field strength at the center of a circular loop. It is

where [latex]R[/latex] is the radius of the loop. This equation is very similar to that for a straight wire, but it is valid only at the center of a circular loop of wire. The similarity of the equations does indicate that similar field strength can be obtained at the center of a loop. One way to get a larger field is to have [latex]N[/latex] loops; then, the field is [latex]B={\mathrm{N\mu }}_{0}I/\left(2R\right)[/latex]. Note that the larger the loop, the smaller the field at its center, because the current is farther away.

Magnetic Field Produced by a Current-Carrying Solenoid

A solenoid is a long coil of wire (with many turns or loops, as opposed to a flat loop). Because of its shape, the field inside a solenoid can be very uniform, and also very strong. The field just outside the coils is nearly zero. (Figure) shows how the field looks and how its direction is given by RHR-2.

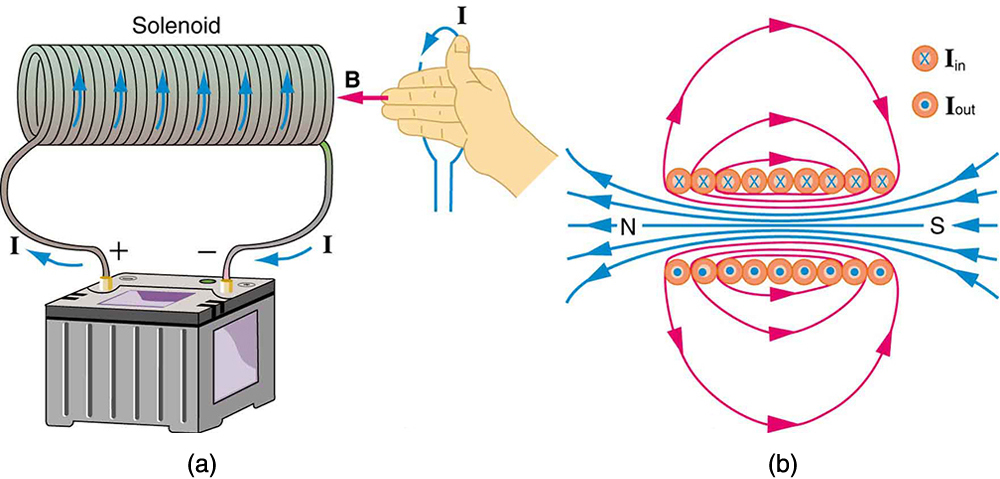
The magnetic field inside of a current-carrying solenoid is very uniform in direction and magnitude. Only near the ends does it begin to weaken and change direction. The field outside has similar complexities to flat loops and bar magnets, but the magnetic field strength inside a solenoid is simply

where [latex]n[/latex] is the number of loops per unit length of the solenoid [latex]n=N/l[/latex], with [latex]N[/latex] being the number of loops and [latex]l[/latex] the length). Note that [latex]B[/latex] is the field strength anywhere in the uniform region of the interior and not just at the center. Large uniform fields spread over a large volume are possible with solenoids, as (Figure) implies.

There are interesting variations of the flat coil and solenoid. For example, the toroidal coil used to confine the reactive particles in tokamaks is much like a solenoid bent into a circle. The field inside a toroid is very strong but circular. Charged particles travel in circles, following the field lines, and collide with one another, perhaps inducing fusion. But the charged particles do not cross field lines and escape the toroid. A whole range of coil shapes are used to produce all sorts of magnetic field shapes. Adding ferromagnetic materials produces greater field strengths and can have a significant effect on the shape of the field. Ferromagnetic materials tend to trap magnetic fields (the field lines bend into the ferromagnetic material, leaving weaker fields outside it) and are used as shields for devices that are adversely affected by magnetic fields, including the Earth’s magnetic field.