6 Membrane Potential
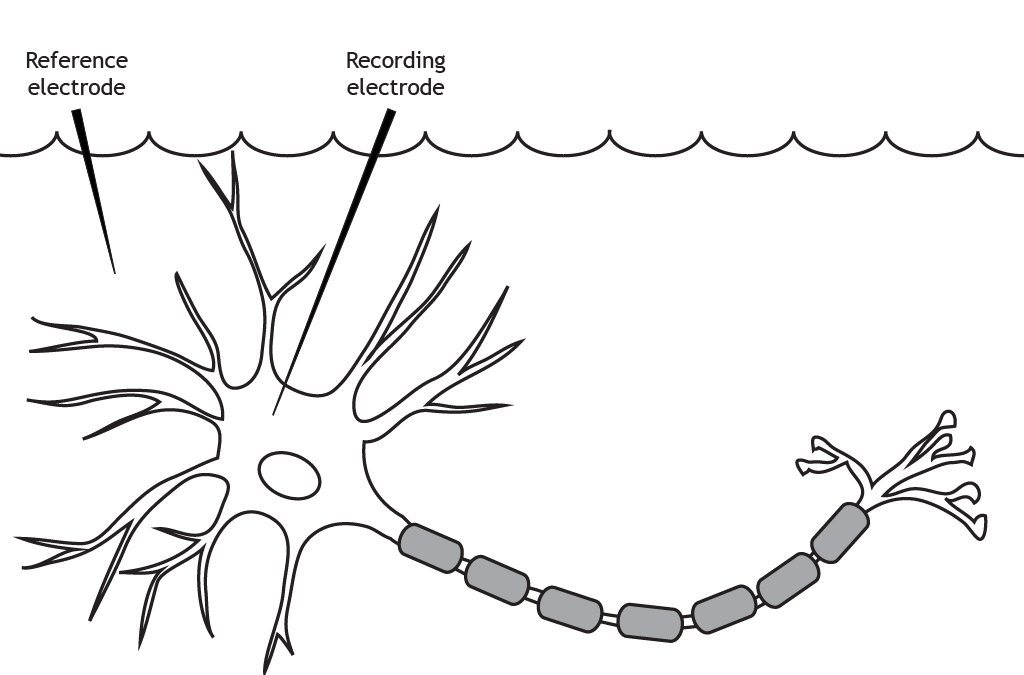
The membrane potential is the difference in electrical charge between the inside and the outside of the neuron. This is measured using two electrodes. A reference electrode (also called the ground electrode) is placed in the extracellular solution. The recording electrode is inserted into the cell body of the neuron.
Terminology
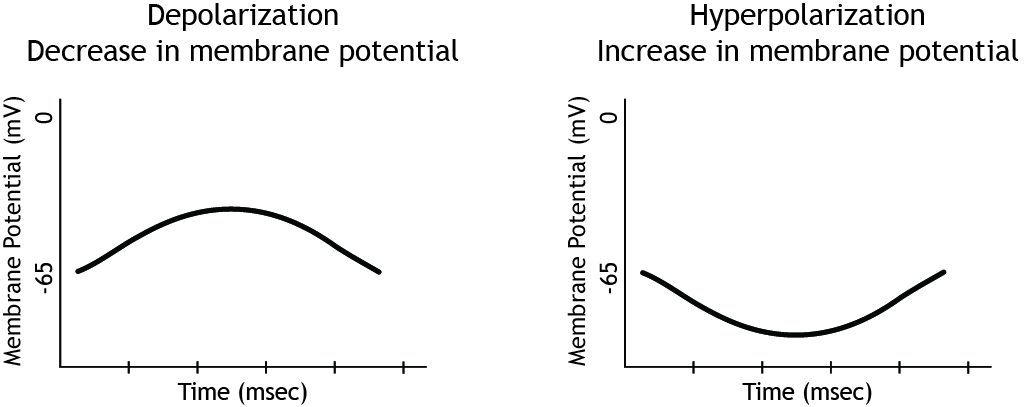
There is more than one way to describe a change in membrane potential. The membrane potential is measured as the difference in charge between the outside of the cell and the inside of the cell. If the membrane potential moves toward zero, that is a depolarization, because the membrane is becoming less polarized—meaning there is a smaller difference between the charge on the inside of the cell compared to the outside. This is also referred to as a decrease in membrane potential. This means that when a neuron’s membrane potential moves from rest, which is typically around -65 mV, toward 0 mV and becomes more positive, this is a decrease in membrane potential. Since the membrane potential is the difference in electrical charge between the inside and outside of the cell, that difference decreases as the cell’s membrane potential moves toward 0 mV.
If the membrane potential moves away from zero, or gets more negative than it was at rest, that is a hyperpolarization because the membrane is becoming more polarized. This is also referred to as an increase in membrane potential.
Voltage Distribution
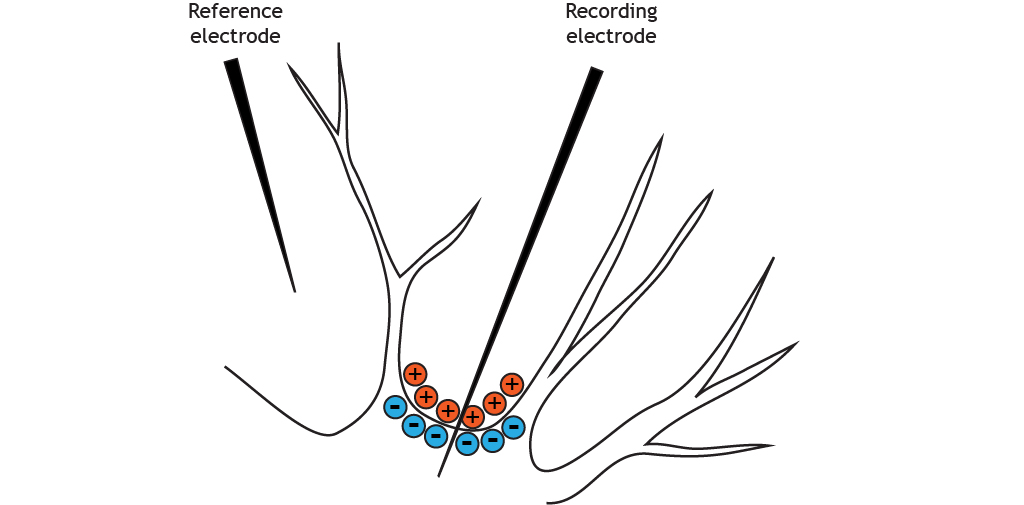
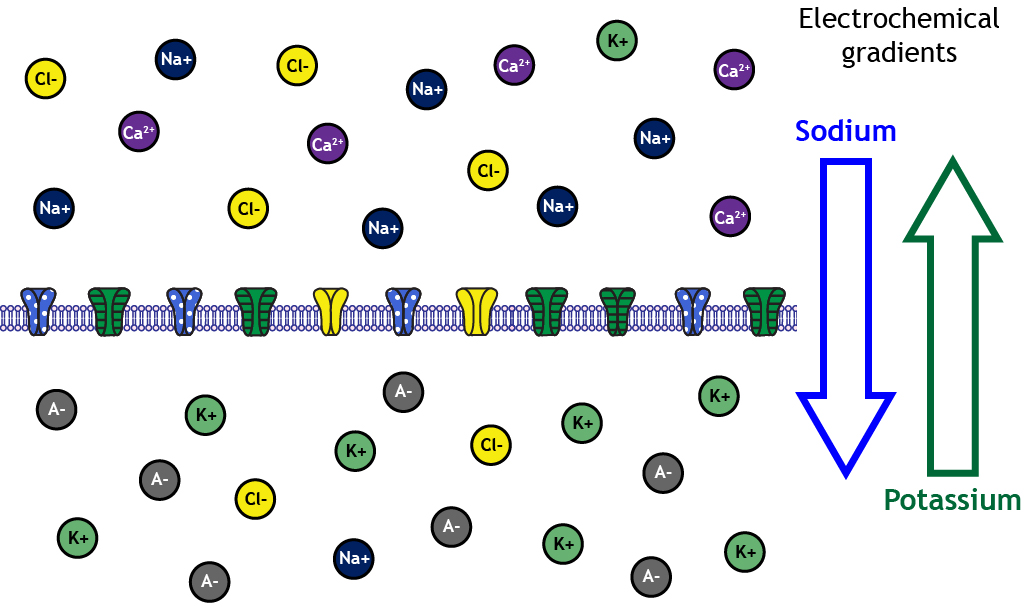
At rest, ions are not equally distributed across the membrane. This distribution of ions and other charged molecules leads to the inside of the cell having a more negative charge compared to the outside of the cell.
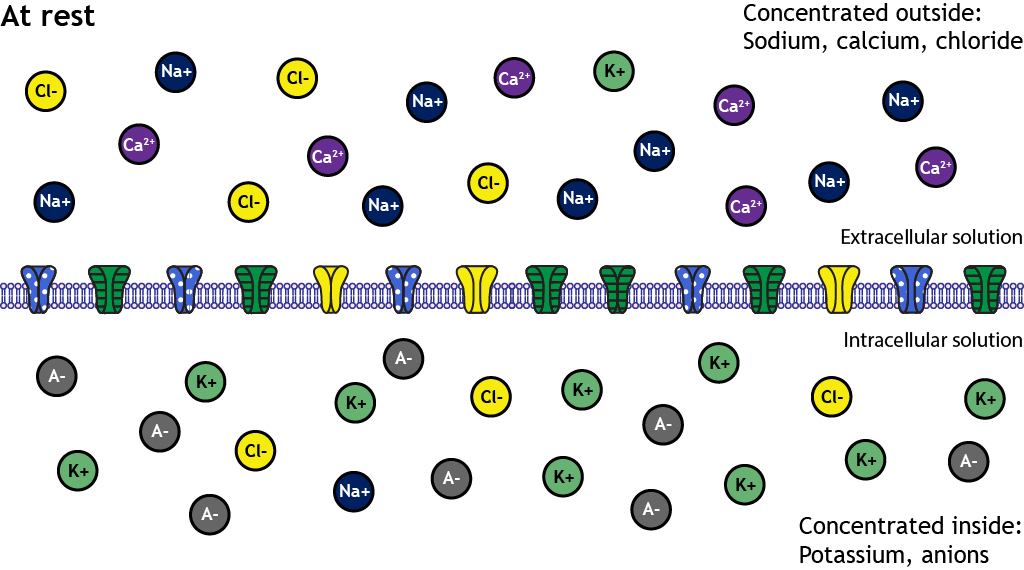
A closer look shows that sodium, calcium, and chloride are concentrated outside of the cell membrane in the extracellular solution, whereas potassium and negatively-charged molecules like amino acids and proteins are concentrated inside in the intracellular solution.
Ion Distribution Creates Electrochemical Gradients
These concentration differences lead to varying degrees of electrochemical gradients in different directions depending on the ion in question. For example, the electrochemical gradients will drive potassium out of the cell, but will drive sodium into the cell.
Equilibrium Potential
The neuron’s membrane potential at which the electrical and concentration gradients for a given ion balance out is called the ion’s equilibrium potential. Let’s look at sodium in more detail:
Example: Driving Forces on Sodium Ions
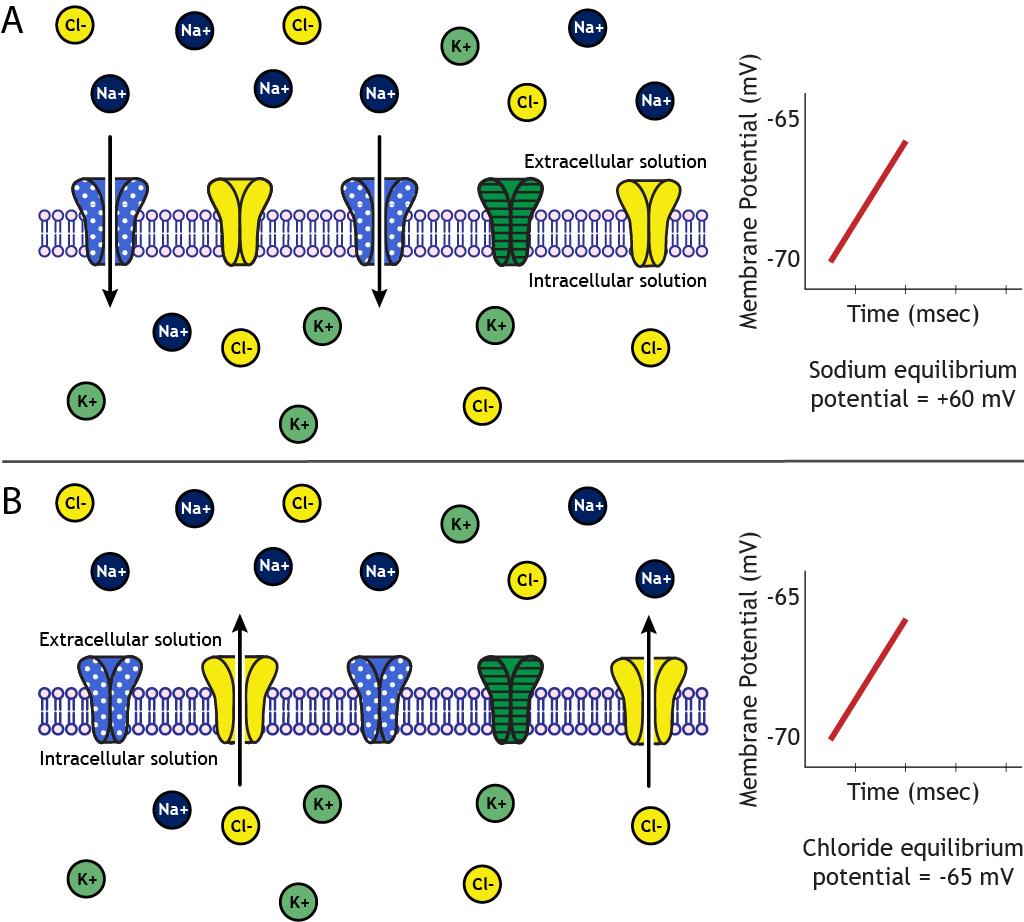
When sodium channels open, the neuron’s membrane becomes permeable to sodium, and sodium will begin to flow across the membrane. The direction is dependent upon the electrochemical gradients. The concentration of sodium in the extracellular solution is about 10 times higher than the intracellular solution, so there is a concentration gradient driving sodium into the cell. Additionally, at rest, the inside of the neuron is more negative than the outside, so there is also an electrical gradient driving sodium into the cell.
As sodium moves into the cell, though, these gradients change in driving strength. As the neuron’s membrane potential become positive, the electrical gradient no longer works to drive sodium into the cell. Eventually, the concentration gradient driving sodium into the neuron and the electrical gradient driving sodium out of the neuron balance with equal and opposite strengths, and sodium is at equilibrium. The membrane potential of the neuron at which equilibrium occurs is called the equilibrium potential of an ion, which is approximately +60 mV for sodium.
Calculate Equilibrium Potential with Nernst Equation
The gradients acting on the ion will always drive the ion towards equilibrium. The equilibrium potential of an ion is calculated using the Nernst equation:
The Nernst Equation
[latex]E_{ion}= \displaystyle \frac{61}{z} log \frac{[ion]_{outside}}{[ion]_{inside}}[/latex]
The constant, 61, is calculated using values such as the universal gas constant and temperature of mammalian cells
Z is the charge of the ion
[Ion]inside is the intracellular concentration of the ion
[Ion]outside is the extracellular concentration of the ion
An Example: Sodium's Equilibrium Potential
[latex]E_{ion}= \displaystyle \frac{61}{z} log \frac{[ion]_{outside}}{[ion]_{inside}}[/latex]
For Sodium:
z = 1
[Ion]inside = 15 mM
[Ion]outside = 145 mM
[latex]E_{ion}= \displaystyle \frac{61}{1} log \frac{145}{15} = 60 mV[/latex]
Predict Ion Movement by Comparing Membrane Potential to Equilibrium Potential
It is possible to predict which way an ion will move by comparing the ion’s equilibrium potential to the neuron’s membrane potential. Let’s assume we have a cell with a resting membrane potential of -70 mV. Sodium’s equilibrium potential is +60 mV. Therefore, to reach equilibrium, sodium will need to enter the cell, bringing in positive charge. On the other hand, chloride’s equilibrium potential is -65 mV. Since chloride is a negative ion, it will need to leave the cell in order to make the cell’s membrane potential more positive to move from -70 mV to -65 mV.
Concentration and Equilibrium Potential Values
We will use the following ion concentrations and equilibrium potentials:
| Ion | Inside concentration (mM) | Outside concentration (mM) | Equilibrium Potential |
|---|---|---|---|
| Sodium (Na+) | 15 | 145 | +60 mV |
| Potassium (K+) | 125 | 5 | -85 mV |
| Chloride (Cl-) | 13 | 150 | -65 mV |
Key Takeaways
- Moving the membrane potential toward 0 mV is a decrease in potential; moving away from 0 mV is an increase in potential
- The distribution of ions inside and outside of the cell at rest vary among the different ions; some are concentrated inside, some are concentrated outside
- Equilibrium potentials are calculated using the Nernst equation
- To predict ion movement, compare the current membrane potential of the neuron with the ion's equilibrium potential. Determine which way the ion needs to move to cause that membrane potential change (i.e. does the ion need to move into the cell or out of the cell?)
Test Yourself!
Attributions
Portions of this chapter were remixed and revised from the following sources:
- Foundations of Neuroscience by Casey Henley. The original work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License
The difference in charge across the cell membrane (between the inside of the cell and the outside of the cell)
The cell body of a neuron. Where the nucleus and organelles are located.
When the membrane potential gets closer to zero
When the membrane potential gets further away from zero
The combination of chemical and electrical gradients
the membrane potential at which the electrical and concentration gradients for a given ion are in balance
allows for passage across the cell membrane
Process by which a high concentration of a substance, given enough time, will eventually diffuse to a lower concentration and settle evenly over the space
electrical forces acting on charged molecules, “pulling” opposite charges together while also “pushing” like charges away from one another
Used to calculate the equilibrium potential of an individual ion

