7 The Membrane at Rest
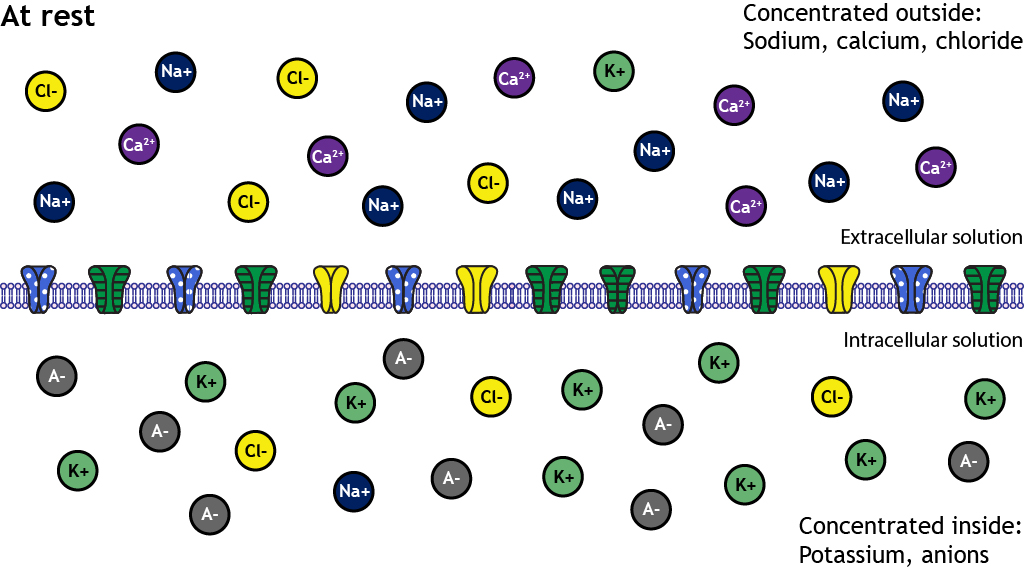
As covered in the previous chapter, at rest there is an uneven distribution of ions on either side of the membrane. The inside of the neuron is more negatively charged than the outside. The resting membrane potential of a typical neuron is around -65mV to -70mV, though it can vary.
Why is the Resting Membrane Potential -65 mV?
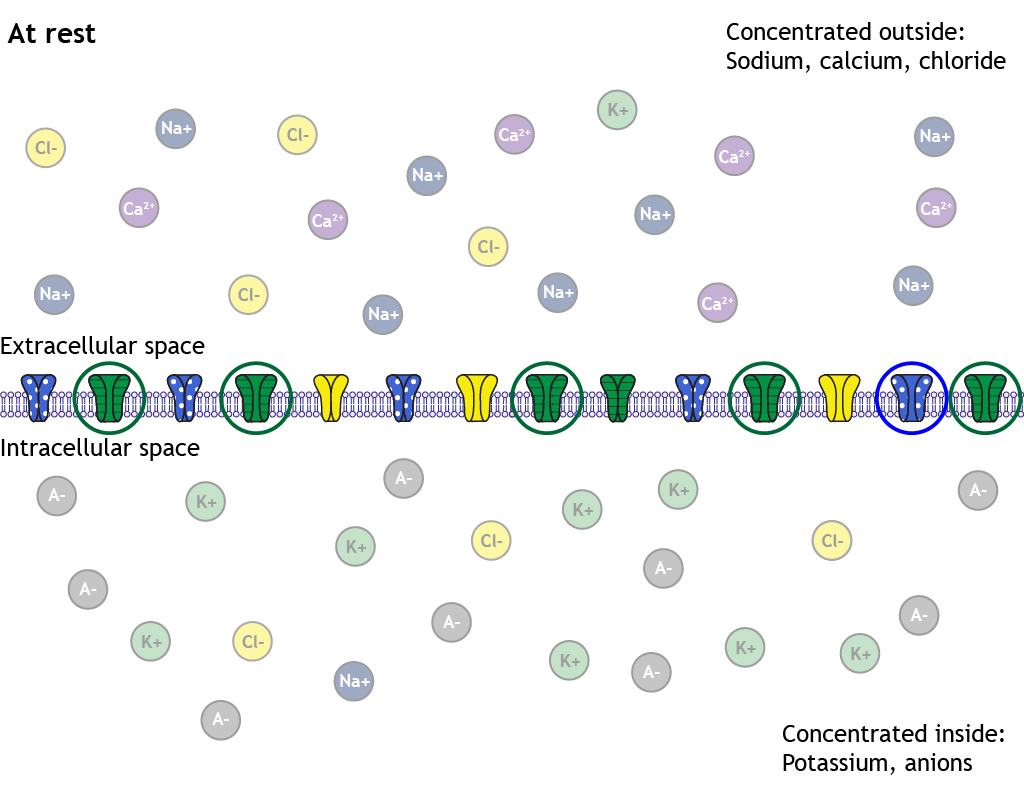
How the ions are distributed across the membrane plays an important role in the generation of the resting membrane potential. When the cell is at rest, some non-gated, or leak, ion channels are actually open. Significantly more potassium channels are open than sodium channels, and this makes the membrane at rest more permeable to potassium than sodium.
1. Potassium Can Cross Membrane at Rest through Leak Channels
Since the membrane is permeable to potassium at rest due to the open non-gated channels, potassium will be able to flow across the membrane. The electrochemical gradients at work will cause potassium to flow out of the cell in order to move the cell’s membrane potential toward potassium’s equilibrium potential of -80 mV.
Resting Membrane Potential Value
The resting membrane potential of a neuron is typically around -65mV to -70mV (but can vary quite a bit). You might ask, though, if the cell has these open non-gated ion channels, and ions are moving at rest, won’t the cell eventually reach potassium’s equilibrium potential if the membrane is only permeable to potassium?
If the open non-gated potassium channels were the only structural ion flow element present in the cell membrane, the membrane potential would eventually reach potassium’s equilibrium potential. However, the membrane has other open non-gated ion channels as well. Although, there are fewer of these channels compared to the potassium channels. The permeability of chloride is about half that of potassium and the permeability of sodium is about 25 to 40 times less than that of potassium. This leads to enough chloride and sodium ion movement to keep the neuron at a resting membrane potential that is slightly more positive than potassium’s equilibrium potential.
2. Intracellular Anions
There are negatively charged anions trapped within the cell that contribute to the negative intracellular charge when compared to the extracellular charge.
3. Activity of the Sodium/Potassium Pump
It is critical the ion gradients that exist across the membrane be maintained for proper neuronal function.
As ions move across the membrane, both at rest and when the neuron is active, the concentrations of ions inside and outside of the cell would change. This would lead to changes in the electrochemical gradients that are driving ion movement. What, then, maintains the concentration and electrical gradients critical for the ion flow that allows the neuron to function properly?
The sodium-potassium pump is the key. The pump uses energy in the form of ATP to move three sodium ions out of the cell and two potassium ions in. This moves the ions against their electrochemical gradients, which is why it requires energy. The pump functions to keep the ionic concentrations at proper levels inside and outside the cell. The pump is removing three positively charged ions from inside the cell and adding two positively charged ions. This leaves the inside of the cell always more negative than the outside of the cell.
Calculating Membrane Potential with Goldman Equation
Importantly, membrane potential is affected by all of the ions that exist around the membrane. It is possible to calculate the membrane potential of a cell if the concentrations and relative permeabilities of the ions are known.
Recall from the last chapter, the Nernst equation is used to calculate one ion’s equilibrium potential. Knowing the equilibrium potential can help you predict which way one ion will move, and it also calculates the membrane potential value that the cell would reach if the membrane were only permeable to one ion. However, at rest, the membrane is permeable to potassium, chloride, and sodium. To calculate the membrane potential, the Goldman equation is needed.
The Goldman Equation
[latex]V_{m}=61 * \log \displaystyle \frac{P_{K}\left[K^{+}\right]_{\text {outside }}+P_{N a}\left[N a^{+}\right]_{\text {outside }}+P_{C l}\left[C l^{-}\right]_{\text {inside }}}{P_{K}\left[K^{+}\right]_{\text {inside }}+P_{N a}\left[N a^{+}\right]_{\text {inside }}+P_{C l}\left[C l^{-}\right]_{\text {outside }}}[/latex]
Like the Nernst equation, the constant 61 is calculated using values such as the universal gas constant and temperature of mammalian cells
Pion is the relative permeability of each ion
[Ion]inside is the intracellular concentration of each ion
[Ion]outside is the extracellular concentration of each ion
Example: The Neuron at Rest
[latex]V_{m}=61 * \log \displaystyle \frac{P_{K}\left[K^{+}\right]_{\text {outside }}+P_{N a}\left[N a^{+}\right]_{\text {outside }}+P_{C l}\left[C l^{-}\right]_{\text {inside }}}{P_{K}\left[K^{+}\right]_{\text {inside }}+P_{N a}\left[N a^{+}\right]_{\text {inside }}+P_{C l}\left[C l^{-}\right]_{\text {outside }}}[/latex]
[table id=2 /]
[latex]V_{m}=61 * \log \displaystyle \frac{1[5]+0.04[145]+0.4[13]}{1[125]+0.04[15]+0.4[150]}= -65 mV[/latex]
Potassium Levels Must be Regulated within the Brain
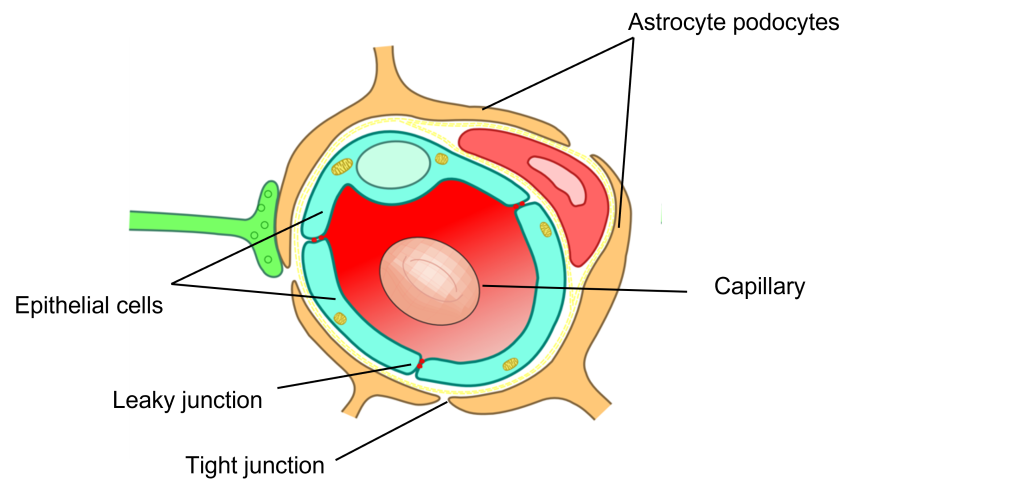
Clearly, potassium levels must be tightly regulated due to the permeability of potassium for the neuronal membrane. Due to the importance of maintaining appropriate potassium levels, the brain has a specialized structure called the Blood Brain Barrier that helps to maintain proper extracellular potassium in the brain by limiting the amount of potassium that can move from capillaries into the brain. Without the blood brain barrier, eating foods that are high in potassium, like a banana, could completely halt the function of your brain!
Typically, capillaries are very leaky vessels, allowing a variety of different nutrients and waste products to pass between the capillaries and the body tissues. The capillaries in the brain, however, are surrounded by astrocytes (a type of glia that we learned about in Chapter 3). The addition of the astrocytes makes it more difficult for substances to pass between the blood and the brain tissue.
In addition to blocking the movement of potassium from the blood to the brain tissue, astrocytes also have potassium pumps in the astrocyte membranes that actively pump potassium out of the extracellular fluid and into the astrocytes to help regulate extracellular potassium levels. This is called potassium buffering.
Key Takeaways
- Non-gated (leak) potassium channels are open at rest causing potassium to have the highest permeability at rest
- Other ion channels (chloride and sodium) are also open, but fewer are open than potassium
- The resting membrane potential of a typical neuron is relatively close to the equilibrium potential for potassium
- The sodium-potassium pump is responsible for maintaining the electrochemical gradients needed for neuron functioning
- The membrane potential can be calculated by knowing the concentrations of each ion inside and outside the cell membrane and the permeabilities of each ion
Test Yourself!
Attributions
Portions of this chapter were remixed and revised from the following sources:
- Foundations of Neuroscience by Casey Henley. The original work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License
Media Attributions
- Blood Brain Barrier © Armin Kübelbeck adapted by Valerie Hedges is licensed under a CC BY (Attribution) license
the membrane potential at which the electrical and concentration gradients for a given ion are in balance
Active transport pump that helps to maintain the electrical and chemical gradients across the cell membrane
The difference in charge across the cell membrane (between the inside of the cell and the outside of the cell)
A diffusion barrier that prevents some of the substances circulating in the blood to pass to brain tissue.

