Present Value Models & Accrual Income Statements

Lindon Robison

8 Present Value Models & Accrual Income Statements

Lindon Robison

Learning goals. After completing this chapter, you should be able to: (1) construct present value (PV) models that are multi-period extensions of accrual income statements (AIS); (2) demonstrate how to properly represent the financial characteristics of an investment using PV models; (3) distinguish between PV models by associating them with AIS earnings and rates of return; and (4) clarify the conditions required for earnings and rates of return on assets and equity to provide consistent rankings. These contributions are intended to help financial managers make better investment decisions.

Learning objectives. To reach your learning goals, you should complete the following objectives:

Describe the similarities and differences between AIS and PV models.
Demonstrate that before and after-tax rates of return on assets (ROA) and equity (ROE) derived from AIS are equivalent to before and after-tax internal rate of return on assets (IRR^A) and equity (IRR^E) derived from multi-period IRR models.
Demonstrate that net present value (NPV) models can be viewed as multi-period present value extensions of EBIT, EBT, and NIAT earning measures.
Solve NPV and IRR models using a generalized Excel template.
Identify the conditions required for consistent earnings and rates of return on assets and equity rankings.

Introduction

^[1]

The development of PV models has a long history. Some of that history is reviewed by Robison and Barry (2020). Relevant to this chapter is work by Osborn (2010), Graham and Harvey (2001), Scott and Petty (1984), and a host of other authors have focused on the possible inconsistency between NPV and IRR rankings and how to resolve the possible conflict. One resolution to the ranking conflict focused on reinvesting cash flow, producing a new class of PV models that Lin (1976) and others have referred to as modified PV models. Related to modified PV models, Beaves (1988) and Shull (1994) describe implicit and explicit reinvestment rates. Magni (2013) proposed a weighted average IRR to resolve PV and IRR inconsistencies. Robison, Barry, and Myers (2015) listed homogeneous size conditions that would guarantee IRR and NPV ranking consistency.

Recent studies have connected PV models to other disciplines. Magni (2020) linked PV models to accounting, finance, and engineering. Robison and Barry (2020) connected AIS accounting measures to PV models by noting the need to account for changes in operating accounts and liquidations of capital accounts in PV models. This chapter emphasizes that by paying attention to AIS and PV model connections we can develop more accurate and transparent PV models and better understand the possible conflict in rankings, depending on whether the focus is on assets or equity.

AIS and PV Models

Accrual Income Statements. AIS measure asset and equity earnings before and after taxes are paid. In addition, when combined with balance sheet data, AIS earning measures can estimate return on assets (ROA), equity (ROE), and after-tax return on equity (ROE(1–T)) where T is the average tax rate. AIS measure revenues and expenses when transactions occur rather than relying exclusively on when cash payments are processed or received (see Harsh, Connor, and Schwab (1981; Lazarus (1987)). To achieve this end, AIS include changes in operating and capital accounts that do not produce cash flow.

PV models defined. This paper defines PV models as multiperiod extensions of AIS. This definition applies because AIS earnings and rates of return have their corresponding measures in PV models. AIS derived ROA, ROE, and ROE(1-T) correspond to PV model derived IRR^A, IRR^E, and IRR^E(1-T). Likewise AIS EBIT, EBT, and NIAT measures correspond to NPV for asset earnings (NPV^A), equity earnings (NPV^E), and after-tax equity earnings (NPV^E(1-T)).

AIS and PV model differences. Despite the correspondence between AIS and PV models, there are some important differences. Consider two. First, AIS are constructed to measure a firm’s financial performance. As a result, they are often ex-post in their focus. PV models consider the financial advisability of an investment whose profitability depends on future cash flows. As a result, PV models are often ex-ante in their focus.

Second, AIS can be constructed to measure rates of return and earnings on assets and equity before and after taxes are paid in one period. PV models can be constructed to measure rates of return and earnings on assets and equity before and after tax are paid for investments that generate returns for several periods. As a result, AIS report earnings at the end of the first period. PV models report the present value of cash flow earned over several periods and the liquidated value of operating and capital accounts at the end of the analysis.

Details included in AIS and PV models. AIS and PV models correspond to and are consistent with each other. This consistency requires that we include the same detail and distinctions in PV models as we include in AIS. This requirement implies that we first need to determine if we are investigating return on assets or equity. Second, we need to account for changes in accounts receivable, inventories, accounts payable, accrued liabilities and capital accounts in both AIS as well as in PV models. Finally, to calculate rates of return on assets and equity requires asset and equity balances besides earnings data. AIS require beginning assets and equity data from balance sheets. PV models also require assets and equity data to determine how investments are supported.

So, what have we learned? PV models are multi-period generalizations of AIS whose future cash flows are evaluated as though they were received in the present period. As a result, we need to be prepared to construct PV models with the same detail included in an AIS. If we fail to include these details, we may misrepresent the present value of the investment’s earnings and rates of return.

AIS Earnings and Rates of Return on Assets and Equity

Earnings on assets. AIS earnings on beginning assets equals:

the difference between cash receipts and the sum of cash cost of goods sold (COGS) and cash overhead expenses (OE), and
changes in the value of the firm’s operating and capital accounts.

A numerical example. We illustrate how to find AIS earnings and rates of return on assets using data that describes the fictional firm Hi-Quality Nursery (HQN) described in Chapter 5. We report the AIS for HQN in Table 8.1.

**Table 8.1. HQN’s 2018 Accrual Income Statement**
	2018
+ Cash Receipts	$38,990
+ Change in Accounts Receivable	($440)
+ Change in Inventories	$1,450
+ Realized capital gains (losses)	$0
Total Revenue	$40,000
+ Cash Cost of Goods Sold	$27,000
+ Change in Accounts Payable	$1,000
+ Cash Overhead Expenses	$11,078
+ Change in Accrued Liabilities	($78)
+ Depreciation	$350
Total Expenses	$39,350
Earnings Before Interest and Taxes (EBIT)	$650
– Less Interest Costs	$480
Earnings Before Taxes (EBT)	$170
– Less Taxes	$68
Net Income After Taxes (NIAT)	$102
– Less Dividends and Owner Draw	$287
Addition to Retained Earnings	($185)

The AIS reported in Table 8.1 organizes cash flow and changes in operating and capital accounts into total revenue and total expenses and reports the difference as EBIT. The HQN EBIT calculation is summarized in equation (8.1). Total revenue equals cash receipts (CR), plus the change in accounts receivable (ΔAR), plus the change in inventory (ΔInv), plus realized capital gains (losses) (RCG). Total expenses equal the sum of cash COGS, plus the change in accounts payable (ΔAP), plus the change in cash overhead expenses (∆OE), plus the change in accrued liabilities (ΔAL), plus the change in the book value of capital assets or depreciation (Dep). EBIT represents HQN’s earnings from its beginning assets that include assets supported by its liabilities or debt.

(8.1) 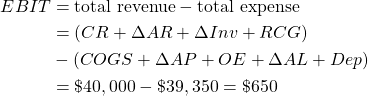$\begin{equation*} \begin{split} EBIT & = \textrm{total revenue} - \textrm{total expense} \\ & = (CR + \Delta AR + \Delta Inv + RCG) \\ & - (COGS + \Delta AP + OE + \Delta AL + Dep) \\ & = \$40,000 - \$39,350 = \$650 \end{split} \end{equation*}$

Rates of return on assets. We find HQN’s ROA by dividing HQN’s EBIT of $650 by its beginning assets (A₀) of $10,000 reported in Table 8.2. HQN’s ROA equals:

(8.2) $\begin{equation*} ROA = \dfrac{EBIT}{A_0} = \dfrac{\$650}{\$10,000} = 6.5\% \end{equation*}$

**Table 8.2. HQN’s Beginning and Ending Balance Sheets**
DATE	12/31/2017	12/31/2018
Cash and Marketable Securities	$930	$600
Accounts Receivable	$1,640	$1,200
Inventory	$3,750	$5,200
Notes Receivable	$0	$0
Total Current Assets	$6,320	$7,000
Depreciable Assets	$2,990	$2,710
Non-depreciable Assets	$690	$690
Total Long-Term Assets	$3,680	$3,400
TOTAL ASSETS	$10,000	$10,400
Notes Payable	$1,500	$1,270
Current Portion Long-Term Debt	$500	$450
Accounts Payable	$3,000	$4,000
Accrued Liabilities	$958	$880
Total Current Liabilities	$5,958	$6,600
Non-Current Long-Term Debt	$2,042	$1,985
Total Liabilities	$8,000	$8,585
Contributed Capital	$1,900	$1,900
Retained Earnings	$100	($85)
Total Equity	$2,000	$1,815
TOTAL LIABILITIES AND EQUITY	$10,000	$10,400

Earnings and rate of return on equity. We find HQN’s earnings on its beginning equity by subtracting from EBIT interest costs (Int) that represent payments for the use of debt and other liabilities and refer to the result as EBT, earnings after interest and before taxes are paid. We find ROE for HQN by dividing EBT by the firm’s beginning equity (E₀) of $2,000 reported in Table 8.2. HQN’s ROE equals:

(8.3) $\begin{equation*} ROE = \dfrac{EBIT - Int}{E_0} = \dfrac{EBT}{E_0} = \dfrac{\$170}{\$2,000} = 8.5\%\end{equation*}$

Earnings and changes in beginning assets and equity. EBIT and EBT earnings on the firm’s beginning assets and equity respectively. These earnings estimates may not equal the actual changes in assets and equity between periods reported in HQN’s balance sheets. To explain, the change in equity between periods reported in Table 8.2 equals ($185), ($1815 – $2,000). However, this value is not equal to EBT of $170 estimated from HQN’s AIS in Table 8.1. The difference between the change in equity and EBT can be attributed to sum of taxes paid equal to $68 and owner draw equal to $287. If we subtract taxes and owner draw from EBT, we find the change in equity between periods of ($185) equal to the actual change in equity reported in Table 8.2.

(8.4) $\begin{equation*} \Delta \textrm{Equity} = EBT - \textrm{taxes} - \textrm{owner draw} = \$170 - \$68 - \$287 = (\$185)\end{equation*}$

Table 8.3 reports a change in HQN’s assets of $400, ($10,400 – $10,000). Meanwhile, HQN’s AIS reports EBIT equal to $650. We can explain part of the difference between EBIT and the actual change in assets by accounting for interest and taxes paid and owner draw. These describe how operating activities can explain the difference between beginning and ending assets. Then if we add the effect of increased liabilities of $585, ($8585 – $8000), and the corresponding increase in assets, we explain the discrepancy. We summarize these results in the Table 8.3.

**Table 8.3. HQN’s EBIT and Change in Assets**
	EBIT	$650
–	Interest paid	$480
–	Taxes paid	$68
–	Owner draw	$287
=	Change in retained earnings	($185)
+	Changes in total liabilities	$585
=	Change in total assets	$400

The main point is that while rates of return on assets and equity reflect some changes in beginning assets and equity—they do not necessarily equal the differences between beginning and ending assets and equity reported in balance sheets. Therefore, we cannot measure rates of return on assets and equity as percentage changes in ending and beginning assets and equity reported in balance sheets.

So, what have we learned? We have learned that EBIT and EBT estimate earnings on beginning assets and equity respectively. EBIT and EBT should be used rather than changes in assets and equity to estimate asset and equity earnings because some changes in assets and equity may be unrelated to investment earnings. We estimate of ROA and ROE by dividing EBIT by A₀ and EBT by E₀ respectively.

AIS and IRR Models

IRR model definition. To build an IRR model, we reorganize an AIS into cash flow and changes in operating and capital accounts. This reorganization allows us to extend an AIS into an n period IRR model by separating n periods of cash flow from the liquidation of operating and capital accounts in the n^th period.

Table 8.4 divides cash flow into cash receipts (CR) and cash expenses (CE). CR include cash sales from operations, reductions in accounts receivable (∆AR < 0), reductions in inventories held for sale (∆Inv < 0) and realized capital gains (RCG). CE include cash COGS, cash OEs, reductions in accounts payable (∆AP < 0), and reductions in accrued liabilities (∆AL < 0).

**Table 8.4. HQN 2018 Cash Flow (Cash Receipts minus Cash Expenses)**
+	Cash Receipts from Operations	$38,990
+	Realized Capital Gains (RCG)	$0
=	Cash Receipts (CR)	$38,990
+	Cash Cost of Goods Sold (COGS)	$27,000
+	Cash Operating Expenses (OE)	$11,078
=	Cash Expenses (CE)	$11,078
	CR – CE	$912

Table 8.5 records changes in operating accounts and depreciation. Changes in operating accounts include ∆AR, ∆Inv, ∆AP, and ∆OE. Note that we include negative changes in operating accounts that produce CR and CE cash flow. We include changes in operating accounts regardless of their sign in Table 8.5 to assure that we are measuring returns and expenses when they occur.

**Table 8.5. HQN 2018 Changes in Operating and Capital Accounts**
+	Change in accounts receivable (∆AR)	($440)
+	Change in inventories (∆Inv)	$1450
–	Change in accounts payable (∆AP)	$1,000
–	Change in accrued liabilities (∆AL)	($78)
=	Changes in operating accounts	$88
–	Depreciation (Dep)	$350
=	Changes in capital accounts	$350
=	Changes in operating and capital accounts	($262)

To summarize the calculations included in Tables 8.4 and 8.5 we express HQN’s EBIT as the sum of cash flow and changes in operating and capital accounts:

(8.5) $\begin{equation*} \begin{split} EBIT & = (CR - CE) + (\Delta AR + \Delta INV - \Delta AP - \Delta AL - Dep) \\ & = \$912 + (\$262) = \$650 \end{split} \end{equation*}$

Notice that the sum of cash flow (CR – CE) recorded in Table 8.4 of $912 plus changes in operating and capital accounts (∆AR + ∆INV – ∆AP – ∆AL – Dep) recorded in Table 8.5 of ($262) equal EBIT of $650 reported in Table 8.1. Were the capital assets sold and their liquidation value not equal to their book value, the difference in capital accounts would be recorded as realized capital gains or losses (RCG) and included in our cash flow measure.

Finally, the EBIT estimate of change in assets minus interest costs equals EBT, the estimate of HQN’s change in equity:

(8.6) $\begin{equation*} EBT = EBIT - Int = \$650 - \$480 = \$170 \end{equation*}$

So, what have we learned? Total revenue in AIS include the difference between CR and CE and changes in operating and capital accounts plus RCG. CR includes cash sales plus reductions in AR (∆AR<0) and Inv (∆Inv<0) accounts. Cash expenses include cash COGS and OEs and reductions in AP (∆AP<0) and AL (∆AL<0) accounts. Changes in operating account include changes between the ending and beginning AR, Inv, AP, and AL accounts over the life of the analysis. When we do not intend to liquidate capital assets at the end of the analysis, we value them at their book value rather than their market value.

AIS and IRR^A Models

Single period IRR^A models. We found ROA and ROE from an AIS by dividing EBIT and EBT by beginning assets A₀ and equity E₀ respectively. We follow a similar procedure when we build PV models. We must account for the beginning value of assets and equity as well as relevant changes in their ending values, including only those changes that affect EBIT or EBT. We are not interested in explaining total changes in equity and assets over the periods of analysis, but only those changes that we can attribute to operating, investing, and financing activities. To that end, we rearrange equation (8.2) and write:

(8.7) $\begin{equation*} A_0 ROA = EBIT\end{equation*}$

Now suppose that we add A₀ to both sides of equation (8.7) and after factoring, divide both sides of equation (8.7) by (1 + ROA) to obtain:

(8.8) 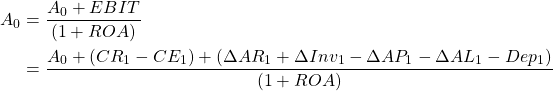$\begin{equation*} \begin{split} A_0 &= \dfrac{A_0 + EBIT}{(1 + ROA)} \\ &= \dfrac{A_0 + (CR_1 - CE_1) + (\Delta AR_1 + \Delta Inv_1 - \Delta AP_1 - \Delta AL_1 - Dep_1)}{(1 + ROA)} \end{split}\end{equation*}$

We simplify equation (8.8) by substituting for A₀, the value of capital accounts V₀ plus the value of current asset accounts AR₀ and Inv₀ plus beginning cash balance Csh₀.

(8.9) $\begin{equation*} A_0 = \dfrac{V_0 + AR_0 + Inv_0 + Csh_0 + (CR_1 - CE_1) + (\Delta AR_1 + \Delta Inv_1 - \Delta AP_1 - \Delta AL_1 - Dep_1}{(1 + ROA)} \end{equation*}$

We simplify equation (8.8) still more by recognizing that the value of capital assets V₀ less depreciation, Dep₁, equals the book value of capital assets V₁^book at the end of the period. However, if the capital assets are actually liquidated, then the liquidation value of capital assets can be written as V₁^liquidation = V₀^book – Dep₁ + RCG. Furthermore, AR₀ + ∆AR₁ = AR₁, and Inv₀ + ∆Inv₁ = Inv₁. Now we can rewrite equation (8.9) as:

(8.10) $\begin{equation*} A_0 = \dfrac{(V_1^{liquidation} + AR_1 + Inv_1 + Csh_0 + (CR_1 - CE_1) - (\Delta AP_1 + \Delta AL_1)}{(1 + ROA)} \end{equation*}$

To write the multi-period equivalent of equation (8.10), we allow time subscripts to range from t = 1, …, n periods. To convert cash flow and liquidated values of noncash operating and capital accounts to their present value, we discount them by (1 + ROA). However, the discount rate in the multi-period equation is not the ROA derived from the one-period AIS but IRR^A, a multi-period average internal rate of return on assets, that we substitute for ROA. We summarize our results in equation (8.11):

(8.11) 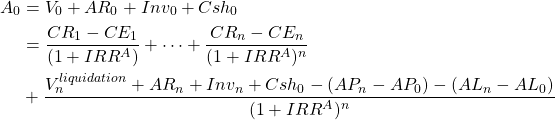$\begin{equation*} \begin{split} A_0 & = V_0 + AR_0 + Inv_0 + Csh_0 \\ & = \dfrac{CR_1 - CE_1}{(1 + IRR^A)} + \cdots + \dfrac{CR_n - CE_n}{(1 + IRR^A)^n} \\ & + \dfrac{V_n^{liquidation} + AR_n + Inv_n + Csh_0 - (AP_n - AP_0) - (AL_n - AL_0)}{(1 + IRR^A)^n} \end{split} \end{equation*}$

To demonstrate equation (8.11) with data from HQN, we set n=1, replace IRR^A with ROA and write:

(8.12) $\begin{equation*} \begin{split} A_0 & = \dfrac{CR_1 - CE_1}{(1 + ROA)} \\ & + \dfrac{V_1^{liquidation} + (AR_1 + Inv_1 + Csh_0) - (AP_1 - AP_0 ) - (AL_1 - AL_0)}{(1 + ROA)} \\ & = \dfrac{\$38,990 - \$38,078}{(1.065)} \\ & + \dfrac{(\$3,400 - \$70) + (\$1,200 + \$5,200 + \$930) - \$1000 - \$78)}{(1.065)} \\ & = \dfrac{\$10,650}{1.065} = \$10,000 \end{split} \end{equation*}$

To explain equation (8.12), we compare the result with HQN’s AIS. We observe CR₁ less CE₁produces $38,990 – $38,078 = $912 (see Table 8.1). Ending period long-term assets (LTA) equal $3,400 (see Table 8.2) from which we subtract purchases minus sales of LTA equal to $100 – $30 = $70. Ending account balances AR1 + Inv1 equal $1,200 + $5,200, and the beginning cash balance is $930. Next, we subtract changes in accounts payable of $1,000 and changes in accrued liabilities of ($78).

AIS and IRR^E Models

We computed ROE by subtracting from EBIT interest paid for the use of debt and divided the result by beginning equity, E₀. To find the multi-period IRR for equity, IRR^E, we subtract in each period t interest cost iD_t–1 where D_t–1 equals the firm’s debt at the end of the previous period and i equals the average cost of debt. To find the amount of equity invested, we subtract from initial assets initial debt D₀. Outstanding debt during the period of analysis collects interest. No changes in debt occur in the last period and debt at the end of the t–1^st period, D_n–1, is retired in the last period. Revising equation (8.10) to account for interest costs and debt and replacing ROE with IRR^E, we can find the multi-period equivalent of ROE, IRR^E. We write:

(8.13) 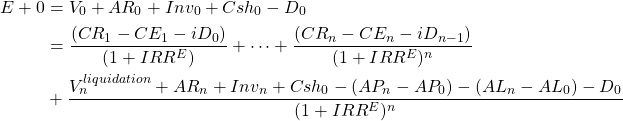$\begin{equation*} \begin{split} E+0 & = V_0 + AR_0 + Inv_0 + Csh_0 - D_0 \\ & = \dfrac{(CR_1 - CE_1 - iD_0)}{(1 + IRR^E)} + \cdots + \dfrac{(CR_n - CE_n - iD_{n-1})}{(1 + IRR^E)^n} \\ & + \dfrac{V_n^{liquidation} + AR_n + Inv_n + Csh_0 - (AP_n - AP_0) - (AL_n - AL_0) - D_0}{(1 + IRR^E)^n} \end{split} \end{equation*}$

To illustrate equation (8.13) with data from HQN, we set n = 1, replace IRR^E with ROE and write:

(8.14) 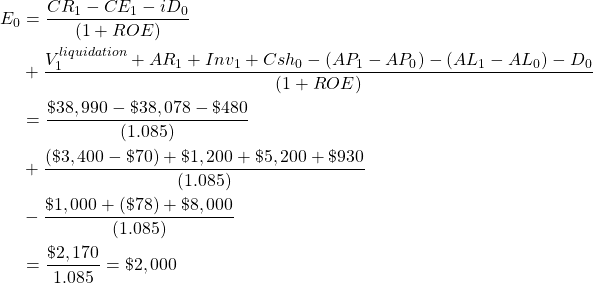$\begin{equation*} \begin{split} E_0 & = \dfrac{CR_1 - CE_1 - iD_0}{(1 + ROE)} \\ & + \dfrac{V_1^{liquidation} + AR_1 + Inv_1 + Csh_0 - (AP_1 - AP_0) - (AL_1 - AL_0) - D_0}{(1 + ROE)} \\ & = \dfrac{\$38,990 - \$38,078 - \$480}{(1.085)} \\ & + \dfrac{(\$3,400 - \$70) + \$1,200 + \$5,200 + \$930}{(1.085)} \\ & - \dfrac{\$1,000 + (\$78) + \$8,000}{(1.085)} \\ & = \dfrac{\$2,170}{1.085} = \$2,000 \end{split} \end{equation*}$

So, what have we learned? We have learned that the multi-period IRR^A and IRR^E models described in equations (8.11) and (8.13) follow AIS construction principles. Investing and borrowing recorded in AIS occur at the beginning of the period. Liquidation of investments and repayments occur at the end of the period. When we extend single period AIS to multi-period PV models, we must allow for multi-period repayments and borrowings and investing and disinvesting. We can easily extend equations (8.11) and (8.13) to account for these possibilities. However, wanting to maintain the focus of this paper on AIS and PV model connections, we omit these complications for now.

AIS Earnings and NPV Models

In the previous sections we derived multi-period IRR^A and IRR^E that correspond to ROA and ROE derived from a one period AIS and beginning assets and equity. Now we introduce multi-period NPV models that correspond to one period AIS earnings, EBIT, EBT, and NIAT. We begin by emphasizing the main difference between IRR and NPV models. IRR models find the rate of return earned by the investment or equity supporting the investment. NPV models measure the earnings realized by transferring funds from a defending investment, the investment in place, to a challenging investment, the investment being considered to replace the defending investment. Thus, NPV models convert multi-period future cash flow and changes in operating and capital accounts from a challenging investment for present dollars at the rate of one plus the defender’s IRR, (1 + IRR).

EBIT and NPV^A earnings on assets. We write NPV for asset earnings by rearranging equation (8.10) and by reinterpreting IRR^A as the internal rate of return on a defending investment.

(8.15) 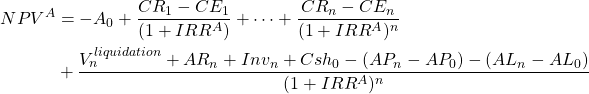$\begin{equation*} \begin{split} NPV^A & = - A_0 + \dfrac{CR_1 - CE_1}{(1 + IRR^A)} + \cdots + \dfrac{CR_n - CE_n}{(1 + IRR^A)^n} \\ & + \dfrac{V_n^{liquidation} + AR_n + Inv_n + Csh_0 - (AP_n - AP_0) - (AL_n - AL_0)}{(1 + IRR^A)^n} \end{split} \end{equation*}$

To demonstrate equation (8.15) with HQN data, we set n = 1, replace IRR^A with ROA, and write:

(8.16) $\begin{equation*} \begin{split} NPV^A & = - A_0 + \dfrac{CR_1 - CE_1}{(1 + ROA)} \\ & + \dfrac{V_1^{liquidation} + AR_1 + Inv_1 + Csh_0 - (AP_1 - AP_0) - (AL_1 - AL_0)}{(1 + ROA)} \\ & = - \$10,000 + \dfrac{\$38,990 - \$38,078}{(1.065)} \\ & + \dfrac{(\$3,400 - \$70) + \$1,200 + \$5,200 + \$930}{(1.065)} \\ & - \dfrac{\$1,000 + (\$78)}{(1.065)} = - \$10,000 + \dfrac{\$10,650}{1.065} = \$0 \end{split} \end{equation*}$

Notice that the NPV^A after exchanging funds from a defender with an identical challenger is zero. But if we found NPV at the end of one period, (IRR^A)(A₀), the product would equal EBIT: (.065)($10,000) = $650 (see equation 8.5). These results emphasize that one important difference between AIS and NPV earnings is that AIS value earnings at the end of the period while PV models value earnings in the present. NPVs value earnings in the present because the present is where we live and make decisions. It should be obviously that if the defender’s IRR were not equal to the challenger’s IRR, then NPV^A would not equal zero. For example, suppose that in equation (8.15), the defender’s IRR were 6%. Then NPV^A would equal $47.17.

EBT and NPVE earnings on equity. We write the NPV for equity earnings by rearranging equation (8.14) and by recognizing that IRR^E is the internal rate of return on equity for a defending investment.

(8.17) 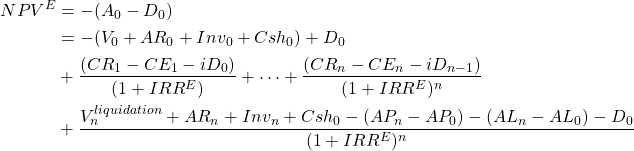$\begin{equation*} \begin{split} NPV^E &= - (A_0 - D_0) \\ & = - (V_0 + AR_0 + Inv_0 + Csh_0) + D_0 \\ & + \dfrac{(CR_1 - CE_1 - iD_0)}{(1 + IRR^E)} + \cdots + \dfrac{(CR_n - CE_n - iD_{n-1})}{(1 + IRR^E)^n} \\ & + \dfrac{V_n^{liquidation} + AR_n + Inv_n + Csh_0 - (AP_n - AP_0) - (AL_n - AL_0) - D_0}{(1 + IRR^E)^n} \end{split} \end{equation*}$

To illustrate equation (8.17) with data from HQN, we set n=1, replace IRR^E with ROE, and write:

(8.18) 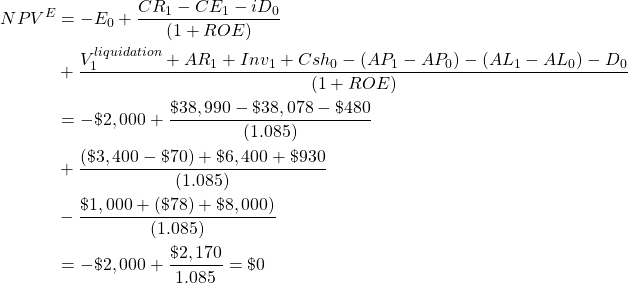$\begin{equation*} \begin{split} NPV^E & = - E_0 + \dfrac{CR_1 - CE_1 - iD_0}{(1 + ROE)} \\ & + \dfrac{V_1^{liquidation} + AR_1 + Inv_1 + Csh_0 - (AP_1 - AP_0) - (AL_1 - AL_0) - D_0}{(1 + ROE)} \\ & = - \$2,000 + \dfrac{\$38,990 - \$38,078 - \$480}{(1.085)} \\ & + \dfrac{(\$3,400 - \$70) + \$6,400 + \$930}{(1.085)} \\ & - \dfrac{\$1,000 + (\$78) + \$8,000)}{(1.085)} \\ & = - \$2,000 + \dfrac{\$2,170}{1.085} = \$0 \end{split} \end{equation*}$

Like the results obtained for NPV^A, NPV^E from exchanging funds from a defender with an identical challenger is zero. But if we found NPV^E at the end of one period, (IRR^E)x(E₀), the product would equal EBT: (.085)x($2,0000) = $170 (see equation 8.6). It should be obvious that if the defender’s IRR were not equal to the challenger’s IRR, that NPV^E would not equal zero. For example, suppose that in equation (8.18), the defender’s IRR were 8%. Then NPV^E would equal $9.26.

So, what have we learned? We have learned that EBIT corresponds to NPV^A. EBT corresponds to NPV^E. We have also learned that IRR and NPV models are distinguished by their reinvestment rate assumptions. IRR models assume that cash flow is reinvested in the challenger and earn the challenger’s IRR. NPV models assume that cash flow is reinvested in the defender and earn the defender’s IRR. Because cash flow in IRR models is discounted and reinvested at the same rate, NPVs or IRR earnings either from assets or equity are always zero.

After-tax ROE and ROA

PV models often focus on after-tax cash flow because it represents what firms/investors keep after paying all their expenses including taxes. In what follows we present tax obligations in a simplified form to illustrate their impact on earnings and rates of return. Our goal is to find the average tax rate T that adjusts ROE to ROE(1–T) and T* that adjusts ROA to ROA(1–T*). We do not try to duplicate the complicated processes followed by taxing authorities to find T and T*. Instead we suggest that the firm pays an average tax rate T or T* on EBT and EBIT respectively.

AIS report taxes paid by the firm and subtracts them from EBT to obtain NIAT. We calculate interest costs by multiplying the average interest rate i times beginning period debt D_t–1 (iD_t-1) and subtract them from earnings to reduce tax obligations. As a result, NIAT represents changes in equity after both interest and taxes have been paid. In 2018, HQN paid $68 in taxes. To find the average tax rate HQN paid on its changes in equity we set taxes equal to the average tax rate T times EBT:

(8.19) $\begin{equation*} \textrm{Taxes} = (T)(EBT) = \$68 \end{equation*}$

Solving for the average tax rate T that HQN paid on its earnings we find:

(8.20) $\begin{equation*} T = \dfrac{\textrm{Taxes}}{EBT} = \dfrac{\$68}{\$170} = 40\% \end{equation*}$

Finally, we adjust ROE for taxes and find HQN’s after-tax ROE to be:

(8.21) $\begin{equation*} ROE(1 - T) = \dfrac{NIAT}{E_0} = \dfrac{\$102}{\$2,000} = 5.1\% \end{equation*}$

AIS and After-tax ROAs. An AIS computes taxes paid by the firm on its return to equity but not on its return to assets. They record only one value for taxes paid and these estimates account for tax saving resulting from interest payments. As a result, we cannot use the average tax rate T calculated for taxes paid on equity earnings to adjust ROA for taxes. To find the average tax rate T* that adjusts ROA to ROA(1 – T*), we calculate taxes “as if” there were no interest costs to reduce the average tax rate to T*. We find ROA(1 – T*) in equation (8.16) as:

(8.22) $\begin{equation*} ROA(1 - T*) = \dfrac{(EBIT - \textrm{Taxes})}{A_0} = \dfrac{(\$650 - \$68)}{\$10,000} = 5.8\% \end{equation*}$

Solving for T* we find:

(8.23) $\begin{equation*} T* = 1 - \dfrac{(EBIT - \textrm{Taxes})}{EBIT} = 1 - \dfrac{(\$650-\$68)}{\$650} = 10.5\% \end{equation*}$

Equation (8.23) emphasizes an important point: adjusting ROE and ROA for taxes nearly always requires different average tax rates. The only time that T = T* is when interest costs are zero. In that case, we can easily demonstrate that T* = T since EBIT = EBT:

(8.24) $\begin{equation*} T = T* = \dfrac{\textrm{Taxes}}{EBIT} = \dfrac{\textrm{Taxes}}{EBT} = 10.5\% \end{equation*}$

After-tax Multiperiod IRR^E(1-T) Model

We are now prepared to introduce taxes into the IRR^E model described in equation (8.13). We begin by solving for NIAT in equation (8.21) and replacing ROE(1-T) with IRR^E(1 – T):

(8.25) $\begin{equation*} NIAT = E_0 ROE(1 - T) = E_0 IRR^E (1 - T) \end{equation*}$

Next, we write NIAT as EBIT adjusted for both interest costs and taxes:

(8.26) $\begin{equation*} NIAT = (EBIT - Int)(1 - T) \end{equation*}$

Then, we substitute for EBIT the right-hand side of equation (8.5) and for NIAT, the right-hand side of equation (8.25) and add time subscripts. The result is equation (8.27).

(8.27) $\begin{equation*} \begin{split} & E_0 ROE(1 - T) \\ & = [(CR_1 - CE_1 - Int_1) \\ & + (\Delta AR_1 + \Delta Inv_1 - \Delta AP_1 - \Delta AL_1 - Dep_1)](1 - T) \end{split} \end{equation*}$

Finally, we add E₀ to both sides of equation (8.27) and after factoring [1 + ROE(1 – T)] and dividing both sides of equation (8.27) by the factor, we obtain:

(8.28) $\begin{equation*} \begin{split} & E_0 = \\ & \dfrac{E_0 + [(CR_1 - CE_1 - Int_1) + (\Delta AR_1 + \Delta Inv_1 - \Delta AP_1 - \Delta AL_1 - Dep_1)](1 - T) }{[1 + ROE(1 - T)]} \end{split} \end{equation*}$

Replacing E₀ with Csh₀ + AR₀ + Inv₀ + V₀ – D₀ in the numerator of (8.28), we can write:

(8.29) $\begin{equation*} \begin{split} E_0 & = \dfrac{Csh_0 + AR_0 + Inv_0 + V_0 - D_0 + [(CR_1 - CE_1 - Int_1)}{[1 + ROE(1 - T)]} \\ & + \dfrac{(\Delta AR_1 + \Delta Inv_1 - \Delta AP_1 - \Delta AL_1 - Dep_1)](1 - T)}{[1 + ROE(1 - T)]} \end{split} \end{equation*}$

Finally, we simplify equation (8.29) by recognizing that

(8.30) $\begin{equation*} V_0 - Dep_1 (1 - T) = V_1^{book} + TDep_1, \end{equation*}$

(8.31) $\begin{equation*} Int_1 = iD_0, \textrm{and} \end{equation*}$

(8.32) $\begin{equation*} \begin{split} & AR_0 + Inv_0 + (\Delta AR_1 + \Delta Inv_1)(1 - T) \\ & = T(AR_0 + Inv_0) + (1 - T)(AR_1 + Inv_1). \end{split} \end{equation*}$

These simplifications allow us to rewrite equation (8.29) as:

(8.33) $\begin{equation*} \begin{split} E_0 & = \dfrac{Csh_0 - D_0 + T(AR_0 + Inv_0) + (1 - T)(AR_1 + Inv_1) + V_1^{book} + TDep_1}{[1 + ROE(1 - T)]} \\ & + \dfrac{[(CR_1 - CE_1 - iD_0) - (\Delta AP_1 + \Delta AL_1)](1 - T)}{[1 + ROE(1 - T)]} \end{split} \end{equation*}$

To verify our results, we substitute HQN numerical values into equation (8.33) and find:

(8.34) $\begin{equation*} \begin{split} E_0 & = \dfrac{\$930 - \$8,000 + [.4(\$1,640 + \$3,750)]}{(1.051)} \\ & + \dfrac{[.6(\$1,200 + \$5,200)] + (\$3,400 - \$70) + [.6(\$350)]}{(1.051)} \\ & + \dfrac{[(\$38,990 - \$38,078 - \$480) - (\$1,000 - \$78)].6}{(1.051)} = \$2,000 \end{split} \end{equation*}$

To write the multi-period equivalent of equation (8.34) we discount n periods of operating income and in the nth period we liquidate operating and capital accounts and replace ROE(1 – T) with IRR^E(1 – T).

(8.35) $\begin{equation*} \begin{split} E_0 & = \dfrac{(CR_1 - CE_1 - iD_0)(1 - T) + TDep_1}{[1 + IRR^E (1 - T)]} \\ & + \cdots + \dfrac{(CR_n - CE_n - iD_{n-1})(1 - T) + TDep_n}{[1 + IRR^E (1 - T)]^n} \\ & + \dfrac{Csh_0 - D_0 + T(AR_0 + Inv_0) + (1 - T)(AR_n + Inv_n)}{[1 + IRR^E (1 - T)]^n} \\ & + \dfrac{V_n^{book} - (AP_n - AP_0 + AL_n - AL_0)(1 - T)}{[1 + IRR^E (1 - T)]^n} \end{split} \end{equation*}$

Capital gains (losses) and taxes. At the end of the analysis, PV models value their capital assets at their book value, or if they liquidate them, they value them at their liquidation value V_n^liquidation. For tax purposes, if the difference between the liquidation and book value of capital assets is positive, (V_n^liquidation – V_n^book) > 0, the firm or the investment has realized capital gains whose after-tax value is (1 – T)(V_n^liquidation – V_n^book) > 0. On the other hand, if the difference is negative (V_n^liquidation – V_n^book) < 0, then the firm has realized a capital loss and earned tax credits whose after-tax value loss is (1 – T)(V_n^liquidation – V_n^book) < 0. To simplify the tax discussion, we ignore the tax rate differences between income, capital gains, and depreciation recapture and apply only one tax rate T, the average of all tax rates. Finally, to adjust capital accounts for taxes, we replace V_n^book in equation (8.28) with what follows:

(8.36) $\begin{equation*} (1 - T)(V_n^{liquidation} - V_n^{book}) + V_n^{book} = (1 - T)V_n^{liquidation} + TV_n^{book} \end{equation*}$

Now we can write the after-tax IRRE model for changes in equity consistent with AIS construction principles.

(8.37) $\begin{equation*} \begin{split} E_0 & = \dfrac{(CE_1 - CE_1 - iD_0)(1 - T) + TDep_1}{[1 + IRR^E (1 - T)]} \\ & + \cdots + \dfrac{(CR_n - CE_n - iD_{n-1})(1 - T) + TDep_n}{[1 + IRR^E (1 - T)]^n} \\ & + \dfrac{Csh_0 - D_0 + T(AR_0 + Inv_0) + (1 - T)(AR_n + Inv_n)}{[1 + IRR^E (1 - T)]^n} \\ & + \dfrac{(1 - T)V_n^{liquidation} + TV_n^{book} - (AP_n - AP_0 + AL_n - AL_0)(1 - T)}{[1 + IRR^E (1 - T)]^n} \end{split} \end{equation*}$

So, what have we learned? We have learned that taxes are intended to be charged on earnings including the cost (interest) of using borrowed funds that support the investment. While most expenses are incurred in exchanges for nondurable goods that are used up in the period’s production, capital investments are only used up over several periods. To account for the periodic costs of using capital assets, we include depreciation as a cost when finding earnings and rates of return. We also use depreciation to generate tax savings.

After-tax Multi-period IRR^A(1–T^*) Model

There is no explicit measure for T* that can be used to find ROA(1 – T*). This peculiar result occurs because taxes must account for interest costs that we do not consider when finding EBIT. Yet, many applied IRR models solve for after-tax return on assets that assume we can measure ROA(1 – T*). Still, we can find such a measure from an AIS allowing us to write:

(8.38) $\begin{equation*} \begin{split} A_0 & = \dfrac{(CR_1 - CE_1)(1 - T*) + T* Dep_1}{[1 + IRR^A (1 - T*)]} \\ & + \cdots + \dfrac{(CR_n - CE_n)(1 - T*) + T* Dep_n}{[1 + IRR^A (1 - T*)]^n} \\ & + \dfrac{Csh_0 + T*Accts_0 + (1 - T*)Accts_n}{[1 + IRR^A (1 - T*)]^n} \\ & + \dfrac{(1 - T*) V_n^{liquidation} + T* V_n^{book} - (AP_n-AP_0 + AL_n - AL_0)(1-T*)}{[1 + IRR^A (1 - T*)]^n} \end{split} \end{equation*}$

The main difference between equations (8.37) and (8.38) is that T is replaced with T*, interest charges are not subtracted from periodic cash flow, and initial liabilities are no longer subtracted. All these changes are required so that earnings can be attributed to beginning assets rather than beginning equity.

Although there is no explicit AIS measure corresponding to equation (8.38), we do know the value of beginning assets A₀ and IRR^A (1 – T*) so we can write the one period HQN numerical equivalent of (8.38) assuming capital assets are valued at their book value:

(8.39) $\begin{equation*} \begin{split} A_0 & = \dfrac{Csh_0 + T*Accts_0 + (1 - T*)Accts_1 + V_1^{book} + T* Dep_1}{[1 + ROA (1 - T*)]} \\ & + \dfrac{[(CR_1 - CE_1) - (\Delta AP_1 + \Delta AL_1)](1 - T*)}{[1 + ROA (1 - T*)]} \\ & = \dfrac{\$930 + \$565.95 + \$5,728 + \$3,330 + \$36.75}{(1.058)} \\ & + \dfrac{[(\$38,990 - \$38,078) - (\$1,000 - \$78 )].895}{(1.058)} \\ & = \$10,000 \end{split} \end{equation*}$

So, what have we learned? We have learned that AIS do not find after-tax earnings on assets because tax laws account for interest payments which are not considered on returns to assets. Still, it is popular to find after-tax rates of return and earnings on assets which requires a special calculation to find the equivalent average after-tax rate.

Rates of Return on Assets and Equity

Miller and Bradford (2000) reviewed and compared rates of return on assets and equity. We agree with their conclusion that the two measures should be viewed as complementary. To describe the relationship between ROE and ROA, we begin with equations (8.2) and (8.3) that employ AIS definitions of ROA and ROE. From these two equations we deduce the rates of return identity:

(8.40) $\begin{equation*} ROE = \dfrac{EBIT - Int}{E_0} = \dfrac{(ROA)(A_0) - (i)(D_0)}{E_0} = \dfrac{(ROA - i)D_0}{E_0} + ROA \end{equation*}$

Note that in equation (8.40) if i = ROA or if D₀ = 0 then ROE = ROA. Note also that ROE and ROA are positively related. Furthermore, if we solve for ROA as a function of ROE, we find the familiar weighted cost of capital (WCC) equation that we illustrate using HQN data:

(8.41) 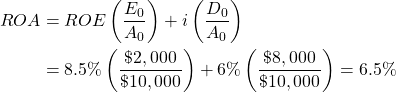$\begin{equation*} \begin{split} ROA & = ROE \left(\dfrac{E_0}{A_0}\right) + i\left(\dfrac{D_0}{A_0}\right) \\ & = 8.5\% \left(\dfrac{\$2,000}{\$10,000}\right) + 6\% \left(\dfrac{\$8,000}{\$10,000}\right) = 6.5\% \end{split} \end{equation*}$

Of course, we are less confident about the relationships in equations (8.40) and (8.41) when measured in multi-period settings where ROA is replaced with IRR^A and ROE is replaced with IRR^E and interest rates and asset and debt levels may vary over time.

We emphasize that both ROA and ROE provide interesting and important information. Financial managers should be interested in what firms and investments can earn independent of how they are financed. Then, if the difference between return on assets and the cost of debt matters, as it should, ROE provides important information for choosing between alternative financing options.

So, what have we learned? We have learned that by adjusting liabilities, interest costs, and tax rates, we can derive PV earning measures corresponding to NIAT, EBIT, and EBT measures calculated in AIS. This provides us an interesting interpretation of PV models. Discounting after-tax multi-period earnings on equity provides a measure corresponding the present value of future NIAT calculations. Discounting before-tax multi-period earnings on assets provides a measure corresponding the present value of future EBIT calculations. Finally, discounting before-tax multi-period earnings on equity provides a measure corresponding the present value of future EBT calculations

Conflicting Asset and Equity Earnings and Rates of Return Rankings

Suppose we are comparing two mutually exclusive challengers, 1 and 2, funded by the same defender and earning rates of return on invested assets of ROA¹ > ROA². Do these results imply that ROE¹ > ROE²? That NPV earnings from assets invested in challengers 1 and 2 satisfy NPV^A1 > NPV^A2? Or, that NPV earnings from equity invested in challengers 1 and 2 satisfy NPV^E1 > NPV^E2?

The answer is that earnings and rates of return on assets and equity are consistent only under limited conditions. These include, A₀ and E₀ must satisfy homogeneity of size conditions and the average interest cost i must be the same for both investments. We demonstrate that if the homogeneity and average interest rate conditions are satisfied, then ROA¹ > ROA² implies ROE¹ > ROE², NPV^A2 > NPV^A1, and NPV^E1 >NPV^E2. To begin, recall equation (8.41) that allows us to write:

(8.42) 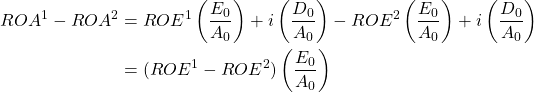$\begin{equation*} \begin{split} ROA^1 - ROA^2 & = ROE^1 \left(\dfrac{E_0}{A_0}\right) + i\left(\dfrac{D_0}{A_0}\right) - ROE^2 \left(\dfrac{E_0}{A_0}\right) + i\left(\dfrac{D_0}{A_0}\right) \\ & = (ROE^1 - ROE^2) \left(\dfrac{E_0}{A_0}\right) \end{split} \end{equation*}$

Therefore, if ROA¹ > ROA², then ROE¹ > ROE². Next, if ROA¹ > ROA², then from equation (8.2), it follows that EBIT¹ > EBIT² and NPV^A1 > NPV^A2 since:

(8.43) $\begin{equation*} NPV^{A1} - NPV^{A2} = \dfrac{EBIT^1 - EBIT^2}{(1 + ROA)} > 0 \end{equation*}$

Finally, if EBIT¹ > EBIT² and interest costs are the same for both investments, then EBT¹ > EBT² and NPV^E1 > NPV^E2 since:

(8.44) $\begin{equation*} NPV^{E1} - NPV^{E2} = \dfrac{EBIT^1 - EBIT^2}{(1 + ROE)} \end{equation*}$

Conflicting rankings may occur when interest rates or debt levels financing the two challengers differ. To illustrate, suppose we decided to rank challengers 1 and 2 that satisfied homogeneity of size conditions for assets and equity and whose ROA1 and ROA2 were equal. Now assume that interest costs for the two investments differed. Then we would rank the two investments based on their asset earnings and rates of return as equal. But for rankings based on equity earnings and rates of return, the investment with the lower interest cost would be preferred. The consequence is that asset-based rankings would be equal and equity-based rankings would be unequal and asset and equity-based rankings would be inconsistent.

To make clear that asset and equity earnings and rates of return may produce conflicting rankings, consider HQN’s one-period ROA of 6.5% ($650/$10,000) and its one-period ROE of 8.5% ($170/$2,000) respectively. Let HQN’s beginning assets and EBIT describe both investments 1 and 2. Now suppose that interest costs for investments 1 and 2 differed. For example, let the average interest rate charged on investment 1 be 6% and 0% for investment 2. As a result, the IRR^E and NPV^E rankings would no longer be consistent with IRRA and NPV^A rankings for investments 1 and 2. We summarize these results in Table 8.6.

**Table 8.6. HQN’s Inconsistent rankings based on asset and equity earnings and rates of return.**
	Investment 1	Investment 2
Asset earnings and rates of return (rankings)
NPV^A (rankings)	EBIT=$650 (1)	>EBIT=$650 (1)
IRR^A (rankings)	$650/$10,000=6.5% (1)	>$650/$10,000=6.5% (1)
Equity earnings and rates of return (rankings)
NPV^E (rankings)	EBT=$170 (2)	EBT=$650 (1)
IRR^E (rankings)	$170/$2,000=8.5% (2)	$650/$2,000=32.5% (1)

One can imagine other less extreme cases in which asset and equity rankings could be inconsistent simply because interest cost influence earnings and rates of return on equity but not for assets.

So, what have we learned? We have learned that earnings and rates of return measures for assets and equity need not provide consistent rankings. As a result, financial managers must carefully whether investment decisions should depend on asset or equity earnings. At the heart of this decision is the importance of debt and interest charges in making investment decisions.

Summary and Conclusions

We now make explicit the main point of this paper. PV models should be constructed as multi-period extensions of AIS. Otherwise, they may misrepresent the financial characteristics of investments and may lead to less than optimal investment decisions. Furthermore, different AIS earnings and rates of return help us distinguish between different NPV models and IRR. These distinctions are important since asset and earning measures on assets and equity may lead to different recommendations.

We emphasize that AIS help us recognize the conditions required for asset and equity earnings and rates of return rankings to be consistent. These insights that we learn from AIS and multi-period extensions of AIS, we believe will help financial managers better understand, build, and interpret PV models. However, these results, also task financial managers with the responsibility to carefully decide whether to base their recommendation on asset or equity earnings and rates of return.

Using the PV models developed in this paper, we can imagine financial managers building Excel templates or similar computerized support systems to solve applied investment problems that include more details than we were able to include in our demonstrations. These details may include more complete description of taxes and allow more investments and disinvestments to occur during the analysis. We wish you all success in this effort—to develop and apply PV models that represent multi-period extensions of AIS.

Questions

How does this chapter define present value models?
Describe two similarities and distinctions between AIS and PV models.
Discuss the following statement. AIS find earnings at the end of the period. PV models value earnings in present dollar equivalents.
AIS EBIT and EBT measure earnings on beginning assets and equity respectively. Do these measures equal the actual change in beginning assets and equity? If not, explain why not?
Please consider the following statement. AIS value cash flows and liquidation of operating and capital accounts at the end of one period. IRR models find the present value of cash flow earnings over several periods and the liquidation of operating and capital account that occurs in the last period. Explain why this difference between AIS and PV models is required. (Hint: why do we limit AIS earning measures to one period while PV models find the present value of investment earnings over several periods.
What is the main difference between IRR^A models and IRR^E models?
One important difference between IRR models and NPV models is their reinvestment rate assumptions. Please describe the reinvestment rate assumptions for IRR and NPV models. What is the NPV value for IRR models?
The cost of operating inputs is included in PV models in the period in which they are paid for with cash. Explain how depreciation estimates the cost of using up capital inputs.
Explain the difference between the average tax rate used to find the after-tax rate of return on equity versus the average tax rate used to find the after-tax rate of return on assets. Also explain why AIS compute earnings on assets (EBIT), equity (EBT), and after-tax earnings on equity (NIAT)–but do not calculate after-tax earnings on assets?
Using the rate of return identify find ROE if ROA=7%, beginning assets are $10,000, the average interest rate is 6%, and liabilities are 75% of assets.
List sufficient conditions that guarantee that earnings and rates of return on asset will generate the same rankings as earnings and rates of return on equity.
If earnings and rates of return on assets and equity provided conflicting rankings, which earnings and rates of return measures would you rely on to choose your investment, on assets or on equity? Defend your preference for either asset or equity rankings.
Use the template described in the appendix to this chapter to find NPV on assets for the following investment.

Appendix to Present Value Models & Accrual Income Statements

Open Green & White Services Excel PV Template

A generalized NPV equation. This appendix operationalizes the concepts presented in this chapter by presenting a generalized present value (PV) template. The PV template corresponds to an accrual income statement (AIS) that measures after-tax returns on equity described in equation (8.37). To solve equation (8.37) for NPVE(1–T) using a generalized PV template, we replace beginning equity E₀ with beginning assets A₀ minus beginning liabilities D0 and discount future cash flow using the defender’s after-tax internal rate of return on equity IRRE(1–T) and by subtracting equity (A₀ – D₀) from both sides of the equation. We rewrite the results as:

(8.A1) $\begin{equation*} \begin{split} NPV^{E(1-T)} & = - (A_0 - D_0) + \dfrac{(CR_1 - CE_1 - iD_0)(1 - T) + TDep_1}{[1 + IRR^E(1 - T)]} \\ & + \cdots + \dfrac{(CR_n - CE_n - iD_{n-1})(1 - T) + TDep_n}{[1 + IRR^E(1 - T)]^n} \\ & + \dfrac{Csh_0 - D_0 + TAccts_0 + (1- T)Accts_n}{[1 + IRR^E(1 - T)]^n} \\ & + \dfrac{(1 - T)V_n^{liquidation} + TV_n^{book} - [AP_n - AP_0 + AL_n - AL_0](1 - T)}{[1 + IRR^E(1 - T)]^n} \end{split} \end{equation*}$

A generalized PV template for finding rolling earnings and rates of return on equity. We now introduce the generalized NPV template corresponding to equation (8.A1). To demonstrate the template, we use data from the Green and White Services investment problem to be introduced in Chapter 10 and represent the defender by solving HQN’s ROE, ROA, T, and T*.

**Table 8.A1. A generalized PV model template with rolling after-tax NPV, AE, and IRR estimates for earnings and rates of return on equity.**
	A	B	C	D	E	F	G	H	I	J	K	L	M	N	O	P	Q	R	S	T	U	V
1	Year	Assets	Debt Capital	Capital Accounts Liquidation Value	Capital Accounts book value	Depreciation (Dep=ΔE)	Asset Operating accounts (AR+INV)	Sales	Cash Receipts (CR=H+ΔG)	Liability Operating Accounts (AP+AL)	Expenses (COGS + OE)	Cash Expenses (CE=K+ΔJ)	Interest Costs (Int=ixC(t-1)	Depreciation tax savings (TxF)	After Tax Cash Flow – (I-L-M)(1-tax rate) +N + ΔC	After Tax Liquidation asset operating accounts – [G(t)-G(0)](1-tax rate)	After Tax Liquidation liability operating accounts [J(n)-J(0)]](1-tax rate)	Sum liquidating capital, operating and debt accounts = (D-E)(1-tax rate)+P-Q+E-C	Sum liquidations + last period cash flow = 0+R	Rolling after-tax NPVs	Rolling after-tax AE	Rolling after-tax IRR
2	0	$40000	$32000	$40000	$40000
3	1	$0	$27200	$30000	$30000	$10000	$1000	$20000	$19000	$0	$9000	$9000	$1920	$4000	$4048	$600	$0	$3400	$7448	-$913	-$960	-6.90%
4	2	$0	$22200	$15000	$15000	$15000	$1200	$30200	$30000	$0	$13500	$13500	$1632	$6000	$9921	$720	$0	-$6480	$3441	-$1033	-$557	3.03%
5	3	$0	$17200	$5000	$5000	$10000	$800	$35600	$36000	$0	$16500	$16500	$1332	$4000	$9901	$480	$0	-$11720	-$1819	$3266	$1202	31.67%
6	4	$0	$12200	$0	$0	$5000	$400	$39600	$40000	$0	$18000	$18000	$1032	$2000	$9581	$240	$0	-$11960	-$2379	$11411	$3226	64.79%

Defender data obtained from HQN is represented in Table 8.A2 below.

**Table 8.A2. Defender’s IRR^E, average tax rate T paid on its equity earnings, and average interest “i” rate paid on its liabilities.**
	A	B
1	IRR^E	0.085
2	T	0.4
3	IRR^E(1-T)	0.051
4	average interest rate i	0.06

Finally, we present in Table 8.A3 GWS equity generated after-tax cash flow during its four years of operation and corresponding after-tax internal rates of return.

**Table 8.A3. GWS equity generated after-tax cash flow during its four years of operations and corresponding after-tax internal rates of return.**
	A	B	C	D	E
1	Economic Life	1 year	2 years	3 years	4 years
2		-$8,000.00	-$8,000.00	-$8,000.00	-$8,000.00
3		$7,448.00	$4,048.00	$4,048.00	$4,048.00
4		-6.90%	$3,440.80	$9,920.80	$9,920.80
5			3.03%	-$1,819.20	$9,900.80
6				31.67%	-$2,379.20
7					64.79%

The results of Table 8.A3 should remind us of the nature of the IRR calculation. After having calculated an investment’s IRR in year t, any positive cash flow in later periods, will increase the investment’s IRR. In the case of GWS, cash flow differ in the last year but still add to the calculated IRR value.

Detailed description of Table 8.A1. The column headings in Table 8.A1 describe exogenous and endogenous variables used to find rolling (every year) NPV and annuity equivalent (AE) estimates and correspond to variables in equation (8.A1). Highlighted data are exogenous often obtained from coordinated financial statements or projected. Data not highlighted are endogenous or calculated. Projecting values in Table 8.A1 is a subject to which we will return in Chapter 11. Now we will describe in more detail the values in Table 8.A1 and their correspondence to variables in equation (8.A1). Columns are indicated by highlighted letters in column titles.

Column A indicates the period t at the end of which financial activity occurs and values are recorded.
Column B line 4 lists total investment amount A₀ including beginning cash C₀, beginning accounts receivable and inventories (AR₀ + Inv₀), plus capital investments V₀.
Column C line 4 lists beginning current liabilities and noncurrent long-term liabilities D₀ supporting the firm’s assets on which interest is paid. Subsequent values in Column C list the amount of outstanding liabilities in each period.
Column D lists the liquidation value of capital investments. Since Table 8.A1 calculates rolling after-tax estimates of NPV, AE, and IRR, we are required to estimate the liquidated value of the investment in each period.
Column E lists the book value of capital investments determined by the initial purchase price and depreciation percentages reported by taxing authorities.
Column F calculates depreciation equal to the change in the investment’s book value.
Column G lists the value of accounts receivable AR_t and inventory Inv_t at the end of period t.
Column H lists total sales during period t.
Column I calculates cash receipts CR_t in period t by adjusting total sales for changes in inventories and accounts receivable.
Column J lists the value of accounts payable AP_t and accrued liabilities AL_t at the end of period t.
Column K lists expenses in period t equal to the cost of goods COGS_t plus overhead expenses OE_t.
Column L calculates cash expenses CE_t in period t adjusted for changes in accounts payable and accrued liabilities.
Column M calculates interest costs iD_t–1 by multiplying periodic liabilities at the end of the previous period D_t–1 by the average interest rate i.
Column N calculates tax savings from depreciation equal to the average tax rate time depreciation in the previous period
Column O calculates after-tax cash flow from operations in period t, equal to (CR_t – CE_t – iD_t-1)(1–T) + TDep_t-1 + ∆D_t). Note that the change in outstanding debt is included because of its impact on cash flow.
Column P calculates cash flow from after-tax liquidation of changes in asset operating accounts (AR_n + Inv_n – AR₀ – Inv₀)(1 – T).
Column Q calculates cash flow from after-tax liquidation of changes in liability operating account (AP_n – AP₀ + AL_n – AL₀)(1 – T).
Column R calculates the cash flow from after-tax liquidation of capital and asset and liability operating accounts.
Column S sums cash flow from after-tax liquidations plus operating cash flow in the last period, required for finding rolling NPV, AE, and IRR values.
Column T calculates rolling after-tax NPVs as though the investment ended in each year using Excel NPV equation by finding the NPV from operations and liquidations.
Column U calculates rolling after-tax AEs associated with the after-tax NPVs for each period using Excel PMT function by finding the payment whose present value equals after-tax NPV for the corresponding period.
Column V calculates rolling after-tax IRRs for each year using Excel IRR function. To find the annual IRRs we calculate the after-tax cash flow for each possible age of the investment reported in Table 8.A2.

Adjusting the PV template to calculate after-tax earnings and rates of return on assets. AIS statements compute earnings before interest and taxes (EBIT), earnings before taxes (EBT), and net income after taxes (NIAT). Table 8.A1 finds the PV model equivalent of NIAT. However, there is no AIS equivalent earnings measure that corresponds to after-tax NPV measures reported in Table 8.A4. This is because taxes paid are reduced by interest costs. However, in this chapter, Chapter 8, we found a method for finding the equivalent average tax rate paid on earnings from assets that enabled us to find rolling after-tax NPVs, AEs, and IRRs for assets.

To adjust equation 8.A1 to find the after-tax earnings and rates of return for assets, we set D₀ equal to zero, we replace the defender’s after-tax IRR for equity IRR^E(1–T) with the defender’s after-tax return on assets IRR^A(1–T*), and we replace the average tax rate T on equity with the average tax rate T* on assets. The revised after-tax NPV calculation for assets is reported as equation 8.A2:

(8.A2) $\begin{equation*} \begin{split} & NPV^{A(1 - T*)} = - A_0 + \dfrac{(CR_1 - CE_1)(1 - T*) + T* Dep_1}{[1 + IRR^A (1 - T*)]} \\ & + \cdots + \dfrac{(CR_n - CE_n)(1 - T*) + T* Dep_n)}{[1 + IRR^A(1 - T*)]^n} \\ & + \dfrac{Csh_0 + T*Accts_0 + (1 - T*)Accts_n}{[1 + IRR^A (1 - T*)]^n} \\ & + \dfrac{(1 - T*) V_n^{liquidation} + T* V_n^{book} - [AP_n - AP_0 + AL_n - AL_0](1 - T*)}{[1 + IRR^A (1 - T*)]^n} \end{split} \end{equation*}$

The PV template equivalent to equation 8.A2 is reported in Table 8.A4.

**Table 8.A4. A generalized PV model template with rolling after-tax NPV, AE, and IRR estimates for earnings and rates of return on assets.**
	A	B	C	D	E	F	G	H	I	J	K	L	M	N	O	P	Q	R	S	T	U	V
1	Year	Assets	Debt Capital	Capital Accounts Liquidation Value	Capital Accounts book value	Depreciation (Dep=ΔE)	Asset Operating accounts (AR+INV)	Sales	Cash Receipts (CR=H+ΔG)	Liability Operating Accounts (AP+AL)	Expenses (COGS + OE)	Cash Expenses (CE=K+ΔJ)	Interest Costs (Int=ixC(t-1)	Depreciation tax savings (TxF)	After Tax Cash Flow – (I-L-M)(1-tax rate) +N + ΔC	After Tax Liquidation asset operating accounts – [G(t)-G(0)](1-tax rate)	After Tax Liquidation liability operating accounts [J(n)-J(0)]](1-tax rate)	Sum liquidating capital, operating and debt accounts = (D-E)(1-tax rate)+P-Q+E-C	Sum liquidations + last period cash flow = 0+R	Rolling after-tax NPVs	Rolling after-tax AE	Rolling after-tax IRR
2	0	$40000	$0	$40000	$40000
3	1	$0	$0	$30000	$30000	$10000	$1000	$20000	$19000	$0	$9000	$9000	$0	$4000	$10000	$600	$0	$30600	$40600	-$1370	-$1440	1.50%
4	2	$0	$0	$15000	$15000	$15000	$1200	$30200	$30000	$0	$13500	$13500	$0	$6000	$15900	$720	$0	$15720	$31620	-$1860	-$1001	3.03%
5	3	$0	$0	$5000	$5000	$10000	$800	$35600	$36000	$0	$16500	$16500	$0	$4000	$15700	$480	$0	$5480	$21180	$2153	$792	7.63%
6	4	$0	$0	$0	$0	$5000	$400	$39600	$40000	$0	$18000	$18000	$0	$2000	$15200	$240	$0	$240	$15440	$10087	$2851	14.85%

Defender data obtained from HQN is represented in Table 8.A5 below.

**Table 8.A5. Defender’s IRR^A, average tax rate T* paid on its assets earnings and average interest i (although irrelevant for the calculations in Table 8.A4).**
	A	B
1	IRR^A	0.065
2	T*	0.105
3	IRRA(1-T*)	0.0582
4	average interest rate i	0.06

Finally, we present GWS asset generated after-tax cash flow during its four years of operation and corresponding after-tax internal rates of return.

**Table 8.A6. GWS asset generated after-tax cash flow during its four years of operations and corresponding after-tax internal rates of return.**
	A	B	C	D	E
1	Economic Life	1 year	2 years	3 years	4 years
2		-$40,000.00	-$40,000.00	-$40,000.00	-$40,000.00
3		$40,600.00	$10,000.00	$10,000.00	$10,000.00
4		1.50%	$31,620.00	$15,900.00	$15,900.00
5			3.03%	$21,180.00	$15,700.00
6				7.63%	$15,440.00
7					14.85%

So, what have we learned? This appendix demonstrated how the PV equations consistent with AIS earnings and rates of return can be operationalized using Excel formulas. The corresponding PV templates demonstrated here could be found at links to this chapter. In general, the templates employ the same level of aggregation as employed when calculating AIS statements. This level of aggregation can be adapted depending on the user’s needs. However, it should be kept in mind that financial ratios used to compare firms within the industry also employ the level of aggregation employed here.

The material in this chapter was adapted from Robison, L.J. and P.J. Barry (2020). “Accrual Income Statements and Present Value Models.” Agricultural Finance Review. ↵

License

Icon for the Creative Commons Attribution-NonCommercial 4.0 International License

Financial Management for Small Businesses, 2nd OER Edition Copyright © 2021 by Lindon Robison is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, except where otherwise noted.