17 Loan Analysis
Lindon Robison
Learning goals. After completing this chapter, you should be able to: (1) understand the different ways interest can be calculated on a loan; (2) recognize the different kinds of interest rates that are used to calculate interest costs on loans; (3) compute comparable effective interest rates; (4) use Excel worksheets to calculate the loan payment, interest rate, term, elasticity of term, and amortization schedule for a particular loan; and (5) find the PV of refinanced and concessionary interest rate loans..
Learning objectives. To achieve your learning goals, you should complete the following objectives:
- Learn the differences between and how to compute the following interest rates: the annual percentage rate (APR), the actuarial rate, and the effective rate.
- Learn how to use the loan equality equation to find a loan’s effective interest rate, its constant payment, its term, and its original loan amount.
- Learn how to find the elasticity relationship between interest rates, loan payments, and the term of the constant payment loan.
- Learn how to create an amortization table for constant payment loans.
- Learn how to find break-even points when refinancing loans.
- Learn how to find the effective rate for several disguised interest rate loans including discount loans and points added loans.
Introduction
Loan formulas and PV models have many similarities. Interest rates on loans are like opportunity costs, the loan amount is like an investment, and loan payments are like an investment’s cash flow. These and other similarities between PV models and loan formulas allow us to use PV tools to analyze different types of loans and interest rates. The next section focuses on alternative interest rate definitions. This chapter will also identify the relationship between the term of a loan and the size of the loan payment. Finally, this chapter finds break-even points when refinancing loans and effective interest rates for a variety of disguised interest rate loans.
Comparing the Actuarial Rate, Annual Percentage Rate (APR), and Effective Interest Rate
Loans charge interest rates of which there are at least three closely related kinds. These rates and their commonly used synonyms are listed below. The interest rate name used in this chapter is italicized. They are:
(1) actuarial rate, compound rate, true rate, or periodic rate (rf);
(2) Annual Percentage Rate (APR), annual rate, or nominal rate (r/m); and
(3) effective interest rate or effective annual rate (re).
Actuarial Rate. In financial transactions, interest may be computed and charged more than once a year. For example, interest on savings deposits is usually calculated on a daily basis while many corporate bonds pay interest on a semiannual basis. The interest rate used in computations for periods of less than one year is called an actuarial interest rate. The actuarial rate is defined as the interest rate per compounding period or the interest rate per period of conversions. It is the actuarial rate used to charge interest on the principal sum during each successive conversion period. For example, consider a 1% actuarial rate charged monthly on $1,000. In this case, in the first month of the loan, 1% of $1,000 or $10 of interest is charged. In the second month, interest is charged on $1,010 equal to $10.10, etc.
Annual Percentage Rate (APR). Let rf represent the APR. Let m stand for the number of times during the year the interest is calculated or charged. Thus, m equals the number of compounding periods per year. The ratio of rf/m is the actuarial rate, the compound rate, the true rate, or the periodic rate.
We find the APR from actuarial rates by expressing the actuarial rate on an annual basis. To convert the actuarial rate to an APR, we multiply the actuarial rate by m. In the previous example, we multiply the actuarial rate of 1% per month by 12 to yield an APR of 12%. When the compound period or conversion period is one year in length, then the actuarial rate and the APR are equal.
Consider two savings institutions, both offering the same APR. The only difference is that institution A offers monthly compounding of interest, while institution B offers annual compounding. Which one should the saver prefer? Obviously, monthly compounding is preferred because the saver earns interest on the interest earned during the same year. With institution B, interest is earned during the year only on the principal saved and on interest earned in previous years.
Effective interest rates. Effective interest rates, designated re, are the actual interest charged measured on an annual basis. When APRs have different numbers of compound periods per year, the different actuarial rates should be converted to their effective interest rates for comparison. The effective rate is obtained by compounding the actuarial rate for a period of one year. As the number of compounding periods per year increases, the difference between the APR and the effective rate increases.
Relationship between interest rates. The relationships between an actuarial rate, an APR, and an effective rate can be easily summarized. Let m be the number of compounding periods per year, let rf be the APR, let rf/m be the actuarial rate, and let re be the effective rate. The relationship between the effective rate re, the APR rate rf, and the actuarial rate rf/m can be expressed as:
(17.1) ![]()
Note that when m = 1, the effective interest rate, the APR rate, and the actuarial rate are equal. However, when m is not 1, the rates are no longer equal. For example, suppose we wish to find the re assuming rf were compounded quarterly. To solve this problem let m = 4, and rf = 12. Substituting .12 for rf and 4 for m in equation (17.1), we obtain the results described in Table 17.1 using Microsoft Excel. In cell B3 we enter the function fx = ((1 + (B1 / B2))^B2) – 1 which returns 12.55%.
| B3 | fx | =(1+B1/B2)^B2 -1 | |
| A | B | C | |
| 1 | APR | 0.12 | |
| 2 | m | 4 | |
| 3 | effective rate | 12.55% | =(1 + APR/m)^m – 1 |
If m is increased to 12, or monthly compounding periods, the effective rate is found as before. Let m = 12, and rf = 12 in equation (17.1). Then
(17.2) ![]()
To solve this equation in Excel, we change cell B2 to 12 and find the effective interest rate to equal 12.68% as shown in Table 17.2.
| B3 | fx | =(1+B2/B3)^B3 -1 | |
| A | B | C | |
| 1 | APR | 0.12 | |
| 2 | m | 12 | |
| 3 | effective rate | 12.68% | =(1 + APR/m)^m – 1 |
A special compounding formula is obtained by allowing the number of periods compounded to be very large. This idea is expressed as:
(17.3) ![]()
which means that as m approaches infinity the effective rate re equals:
(17.4) ![]()
To solve this problem using Excel, we use the EXP function. In Excel, Euler’s number “e” is found as the function EXP(1) and 12% compounded continuously can be calculated as fx = EXP(.12) – 1 = 12.75. Using the previous cell designation, to find the value of continuously compounding of 12% we would enter the formula in B3 as: fx = EXP(B1) – 1 = 12.75.
| B3 | fx | =EXP(B1) – 1 | |
| A | B | C | |
| 1 | APR | 0.12 | |
| 2 | m | Infinite | |
| 3 | effective rate | 12.75% | =EXP(APR) – 1 |
Constant Payment Loans
Having defined interest rates in financial models, we now use PV models to analyze the most common type of loan, the constant payment loan. Constant payment loans are repaid with a series of equal payments A at equal time intervals. These payments may occur m times during a year over n years, yielding a total of mn payments.
The fundamental equality is that the sum of the loan payments discounted at the actuarial interest rate must equal the amount loaned. The relationship between loan amount, L0, received in time-period zero, with payment A, made for mn periods, at actuarial interest rate (rf/m) beginning in period one, is:
(17.5) 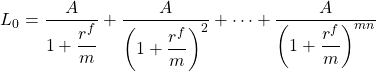
In this formula, the actuarial rate (rf/m) is the IRR for the PV model, and since loan payments are constant, it is unique.
Fortunately, the calculations described in equation (17.5) can be easily performed using Excel. We calculate L0 in the following example.
Example 17.1. Loan amount supported by a constant payment loan. Suppose a borrower can make constant payments of $150 per month for 48 months (four years). The borrower wants to know what size loan can be repaid if the APR interest rate is 5% and the actuarial rate is .05/12 = .42%. Using equation (17.5) we can solve for the loan amount supported by the constant loan payment of $150 using the Excel formula in Table 17.4 below:
| B5 | fx | =PV(B1/B2,B2*B3,B4,,0) | |
| A | B | C | |
| 1 | rate | .05 | |
| 2 | m | 12 | |
| 3 | n | 4 | |
| 4 | pmt | -150 | |
| 5 | PV | $6,513.44 | =PV(rate/m,mn,pmt,,0) |
The answer displayed is: $6,513.44. In other words, 48 monthly payments of $150 on a loan charging a 5% APR interest rate and a monthly actuarial interest rate of .42% will repay a loan in the amount of $6,513.44.
Fortunately, Excel can also solve for the constant payment if the loan amount, term, and interest rate are known. A constant payment loan problem is described in Example 17.2.
Example 17.2. Constant Payment Loan Annuities. Suppose $5,000 is borrowed from a lending institution for five years at an APR of 12% or a monthly actuarial rate of 1%. The loan is to be repaid with 60 equal monthly installments. What is the payment or annuity necessary to retire the loan?
We solve for the loan payment using Excel’s PMT function in Table 17.5. The answer displayed is: –$111.22 which means that 60 payments of $111.22 on a loan charging 12% APR interest and a monthly actuarial interest rate of 1% will repay a loan in the amount of $5,000.
| B4 | fx | =PV(B1/B2,B2*B3,B5,,0) | |
| A | B | C | |
| 1 | rate | 0.12 | |
| 2 | m | 12 | |
| 3 | n | 5 | |
| 4 | pmt | ($111.22) | =PMT(rate/m,mn,PV,,0) |
| 5 | PV | $5,000.00 | |
Finally, consider a loan problem where the unknown variable is the term of the loan. We introduce such a problem in Example 17.3 and the Excel solution in Table 17.6.
Example 17.3. Loan term required to retire a constant payment loan. Suppose a borrower can make constant payments of $150 per month. The borrower wants to know how many monthly payments will be required to retire a loan of $8,000 if the APR interest rate is 6% and the monthly actuarial rate is .5%.
We solve the equation using Excel’s NPER function shown in Table 17.6. The answer displayed is 62.19 which means that 62 regular payments and one partial payment will be required to retire a loan of $8,000 if the APR interest rate charged on the loan is 6%.
| B6 | fx | =NPER(B1/B2,B4,B5,,0) | |
| A | B | C | |
| 1 | rate | 0.06 | |
| 2 | m | 12 | |
| 3 | n | ||
| 4 | pmt | -150 | |
| 5 | PV | $8,000.00 | |
| 6 | nper | 62.18593 | =NPER(rate/m,pmt,PV,,0) |
Comparing Interest Paid, Loan Term, and Payment Amounts for Constant Payment Loans
An important relationship exists between the loan’s term and total interest paid. To illustrate, consider a $30,000 loan at 15% APR to be repaid in monthly payments over 30 years. The monthly payment for this loan is $379.33. Total interest TI paid on a constant payment loan is found by multiplying the constant loan payment A times the term of the loan mn, minus the amount of the loan L0:
(17.6) ![]()
In this case, the total interest paid is $106,560.
Increasing the payment amount by 10% to $417.27 reduces the term of the loan by 48% to just over 15.36 years (verify the results above using Excel). Meanwhile, total interest paid is reduced by 56% to $46,961.
The term reduction in response to an increased loan payment is not always so significant. For example, if the above loan had an 8% APR, the monthly payment would equal $220.13 instead of $379.22. Increasing the payment by 10% would decrease the term of the loan by only 27% from 30 years to 21.93 years, and the total interest paid would be decreased by 32% from $49,247 to $33,722.
It would be useful to know how changing the term of the loan affects payment size and total interest paid. It can be shown that as mn becomes large, the payment A approaches the interest cost per period, i.e., the smallest payment possible equals the interest charged on the outstanding loan balance. If the borrower wished to minimize his or her payment, the appropriate term is the one that permits the borrower to repay only interest. The shortest repayment period, on the other hand, is one. Obviously, there is a trade-off between the size of the loan payment and the length of the loan.
The point elasticity of term, measured in years n with respect to the payment A, measures the percentage change in the term n in response to a 1% change in the loan payment. The term elasticity, E(n,A), has been calculated as:
(17.7) ![]()
For example, a 30-year loan and an APR of 15% would have an elasticity of term equal to:
(17.8) ![]()
In other words, increasing the payment by 1% would decrease the term by approximately 19.78%. In contrast, the arc elasticity, rather than the point elasticity, compares the percentage change in the loan term to a 10% increase in the loan payment and finds the percentage change in the term to equal 48%, or an arc elasticity of term equal to 4.8%. Note that a point elasticity of 19.78% versus an arc elasticity of 48% is the result of comparing large changes in loan payments of 10% versus comparing tiny changes in loan payments (e.g. .00001%). See Table 17.7 of point elasticities below.
| n / r % | 1% | 5% | 7.5% | 10% | 15% | 20% |
| 1 | 1.01 | 1.03 | 1.04 | 1.05 | 1.08 | 1.11 |
| 5 | 1.08 | 1.14 | 1.21 | 1.30 | 1.49 | 1.72 |
| 10 | 1.17 | 1.30 | 1.49 | 1.72 | 2.32 | 3.19 |
| 15 | 1.26 | 1.49 | 1.85 | 2.32 | 3.77 | 6.36 |
| 20 | 1.37 | 1.72 | 2.32 | 3.19 | 6.36 | 13.40 |
| 25 | 1.49 | 1.99 | 2.94 | 4.47 | 11.07 | 29.48 |
| 30 | 1.49 | 2.32 | 3.77 | 6.36 | 19.78 | 67.07 |
| 60 | 2.99 | 6.36 | 19.78 | 67.07 | 900.23 | 13,563.00 |
Example 17.4. Term and Loan Payment Trade-Offs. Lucy Landlord is financing the renovation of a property. She needs a loan for $28,000. Her lender offers her a loan for 20 years at the current interest rate of 15%. She calculates her annual payment to be $4,473.32. If she increases her payment by 1% to $4,518.05, her term is reduced to 19 years, or a reduction of 5%. This percentage reduction is nearly equal to the tabled value of 6.36 in the Table 17.1, found at the intersection of the row labeled 20 and the column labeled 0.15. Large percentage increases in A, such as 10%, may not be accurately reflected in the table of point elasticities. This is because the percentage changes in n with respect to A are large compared to the very small changes in n with respect to A used to calculate the table.
Creating an Amortization Table for Constant Payment Loans
The word “amortize” originally meant “to kill.” Thus when we amortize a loan, we kill or extinguish it by making regular payments—killing the loan if you will. One feature of the constant payment loan is that, while the loan payment is constant, the amount of the payment devoted to paying off the loan—the principal portion of the payment—and the amount of the payment devoted to paying the interest on the loan are constantly changing. As the loan principal is reduced or killed off, the amount of the payment devoted to interest charges is reduced and the amount of the payment devoted to reducing the loan is increased. Lending institutions, when asked, will provide amortization tables that detail the amount of interest and principal paid on each payment during the life of the loan. Fortunately, Excel provides us the tools needed to create our own amortization tables.
Finding principal portion of the tth loan payment using Excel. The Excel PPMT function can be used to find the principal portion of the tth loan payment. The function is expressed as:
(17.9) ![]()
To illustrate the PPMT function, consider at $25,000 loan to be repaid in monthly installments for four years. The APR for the loan is 5%. We want to know what portion of the 5th payment (period) will be applied to the loan’s principal. The Excel solution is represented in Table 17.8.
| B6 | fx | =PPMT(B1/B2,B4,B2*B3,B5,,0) | |
| A | B | C | |
| 1 | rate | 0.05 | |
| 2 | m | 12 | |
| 3 | n | 4 | |
| 4 | period | 5 | |
| 5 | PV | $25,000 | |
| 6 | Principal paid | ($479.47) | =PPMT(rate/m,period,m*n,PV,,0) |
It turns out that $479.47 of the 5th payment is applied to the outstanding loan principal. In addition, students may verify that the principal portion of the 25th payment is $521.05. This is because the outstanding principal on which interest is charged decreases over the life of the loan. As interest decreases, more of the loan payment can be applied to the outstanding loan principal.
Finding interest payment IP(t) on the tth loan payment using Excel. The Excel IPMT function can be used to find the interest portion of a loan payment in the tth period and is expressed as:
(17.10) ![]()
To illustrate the IPMT function, we return to the earlier example: a loan amount of $25,000, a term of 48 monthly payments, at 5% APR, and a desire to find the interest paid on the 5th loan payment. We illustrate the Excel solution for finding interest paid on the tth period. The solution is entered in cell B8 as $54.68. Table 17.9 describes the solution in more detail.
| B6 | fx | =IPMT(B1/B2,B4,B2*B3,B5,,0) | |
| A | B | C | |
| 1 | rate | 0.05 | |
| 2 | m | 12 | |
| 3 | n | 4 | |
| 4 | period | 5 | |
| 5 | PV | $25,000 | |
| 6 | Interest paid | ($96.26) | =IPMT(rate/m,period,m*n,PV,,0) |
Together, the interest payment of $96.26 and the principal payment of $479.47 equals the constant loan payment of $575.73.
PVs of Special Loans
Loans and credit (one’s borrowing capacity) make possible a modern economy and successful firms. Sometimes sellers offer special loan arrangements to encourage the potential buyers to purchase their products. These may include concessionary interest rate loans, skip payment loans, skip principal payment loans, variable interest rate loans, and balloon payment loans. Other times firms may want to expand their investment base and need to refinance their loans, or decreases in interest rates may provide them an incentive to refinance. Fortunately, all of these special loans can be analyzed using PV models developed earlier. We consider the benefits and costs of several special loans in what follows.
Concessionary Interest Rate Loans
A concessionary interest rate loan is one whose interest rate is below the market interest rate. Were the issue to exchange an old loan for a new one at a lower interest rate, there wouldn’t really be much of a decision to be made. However, concessionary interest rate loans are often involved in trade-offs. For example, a concessionary interest rate loan may be offered as an incentive to make a long-term purchase—and the borrower wants to determine if the NPV of the loan is recaptured in the investment’s higher cost? Or, suppose that the economy has exerted downward pressure on interest rates. But in order to refinance, borrowers must pay a percentage of the loan to refinance. In this instance, borrowers may want to know, what percentage of the loan, points, can they afford to pay and still break-even?
Three steps for evaluating concessionary interest rate loans. To evaluate a concessionary interest rate loan, we follow three steps. First, we find the loan payment of the concessionary interest rate loan. Second, we find the PV of the concessionary loan payments using either the market interest rate or the interest rate on the original loan as the defender’s IRR. And third, we find the NPV of the concessionary interest rate loan by subtracting from the loan the PV of the concessionary interest rate loan. We now illustrate how to evaluate concessionary interest rate loans.
Example 17.5. Finding the NPV of a concessionary interest rate loan. Suppose that you want to buy a used car whose price is listed at $8,000. To encourage you to make the purchase, the car salesperson offers you a concessionary interest rate loan of i = 1% while the opportunity costs of capital, your IRR, is r = 8%. If the loan is to be repaid over five years of monthly payments, you ask: what is the NPV of the concessionary rate loan? You might also ask: accounting for the PV of the used car loan, what is the actual price of the used car?
To find the value of the seller’s concessionary interest rate loan, we follow the three steps outlined earlier. First, using Excel financial spreadsheet, we calculate the loan payment (PMT) of the concessionary interest rate loan and report our results in Table 17.10 below.
| B4 | fx | =PMT(B1/B2,B2*B3,B5,,0) | |
| A | B | C | |
| 1 | rate | 0.01 | |
| 2 | m | 12 | |
| 3 | n | 5 | |
| 4 | pmt | ($136.75) | =PMT(rate/m,m*n,PV,,0) |
| 5 | PV | $8,000.00 | |
Our calculations find that a loan payment of $136.75 (pmt) is sufficient to repay an $8,000 loan (PV) at an APR of 1% (rate), with monthly payments (m) over five years (n).
Step two discounts the concessionary interest rate loan payments using the borrower’s IRR of 8%/12. The results are summarized in Table 17.11 below.
| B5 | fx | =PV(B1/B2,B2*B3,B4,,0) | |
| A | B | C | |
| 1 | rate | 0.08 | |
| 2 | m | 12 | |
| 3 | n | 5 | |
| 4 | pmt | ($136.75) | |
| 5 | PV | $6,744.30 | =PV(rate/m,m*n,pmt,,0) |
The calculations reported in Table 17.11 find that the present value of the concessionary interest rate loan of $8,000 is equal to $6,744.30.
Step three calculates the NPV for the concessionary interest rate loan by subtracting from the original loan of $8,000 the discounted present value of the concession interest loan equal to $6,744 and finds:
(17.11) ![]()
Once you know the NPV of the concessionary rate loan, you can negotiate—will the seller lower the price by more than the NPV of the concessionary rate loan if you provide your own financing or pay with cash?
The Refinance Problem
A common financial transaction is the refinancing of a constant payment loan. If the current interest rate is less than the interest rate on one’s existing loan, a reasonable borrower would refinance. But what if refinancing requires a fee, a percentage of the new loan, to be paid at the loan closing? We want to know what the borrower can afford to pay as a refinancing cost, or points of the loan, to break even. Finding break-even points is what we do next. We will use as our starting point the numbers introduced into the previous example.
The refinance problem is clearly an NPV problem. Its solution requires that we identify the defending and challenging investments. The defender in this case is the borrower current loan. The challenger is the new loan with its reduced interest rate and points charged to close the loan. What the borrower will earn on the loan is not relevant here because we assume that those earnings will be the same regardless of whether they are financed with the new loan or continue to be financed with the old loan.
Example 17.6. Finding break-even points for a refinanced constant payment loan. To solve a refinance problem with points, we recognize that the breakeven points (p) equate the cost of refinancing the loan with the NPV of the refinanced loan. Let the loan (L0) times points charged to refinance the loan equal the NPV of the new loan. Setting refinancing costs equal to the NPV of the new loan, using data from Example 17.5 we write:
(17.12) ![]()
Then solving for points p as a percentage of the refinanced loan, we divide both sides of equation 17.12 by the loan amount L0 and find:
(17.13) ![]()
In words, equation (17.13) computes the points we can pay to refinance an existing loan at a concessionary interest rate and still break even. In this example, break-even points equal 15.7%.
Moderated Payment Loans
Sometimes, we borrow for increased liquidity. Small to medium size firms often face variability of cash receipts that do not coincide with expenses. This means that a firm’s liquidity measures such as the current ratio (CT) or the times-interest-earned (TIE) ratio may also vary significantly over time, creating liquidity needs—that are often addressed with increased borrowings. And sometimes, borrowers may apply for loans because the original loan was written for a much shorter period than the investment’s productive life creating a mismatch between the term of financing and producing activities of the firm. Whatever the case, liquidity concerns may require the firm to renegotiate the terms of their loans with their lenders to solve liquidity needs.
Increasing a loan’s term. Consider a moderated payment loan designed to reduce immediate liquidity needs. We use as our example, the loan described in Example 17.2. In this case the required payment was found to equal $111.22. To improve liquidity, suppose the borrower asks the lender to increase the term of the loan by 12 monthly payments. What would be the new loan payment? Resolving the Excel PMT function returns:
(17.14) ![]()
Now a loan payment of $97.75 will retire a loan of $5,000 with 72 payments rather than 60 payments at an actuarial rate of 1%. The loan payment is reduced from $111.22 to $97.75. In this example, the term increased by 12, from 60 months to 72 months or 20% while the payment decreased by [($111.22-$97.75)/$111.22] = 12% and the elasticity of term is 20%/12% or 1.67% Compare this result with those in Table 17.7 at the intersection of column headed by 1% and row labeled 60. Can you explain why there is a difference from the results above and those in Table 17.7? (Hint: can you recall the difference between elasticity measured at a point versus elasticity measure over some interval?)
Skip payments and student loans. Sometimes, we borrow funds to accommodate immediate liquidity needs, expecting that sometime in the future our liquidity will improve and allow us to repay our loans. Such an incentive exists for many students whose incentive for borrowing is to delay making interest and loan payments until after graduating from school.
Loans that delay interest and principal payments, we refer to as skip payment loans. The attractive feature of a skip payment loan is that you don’t have to make payments until after graduation. The not so nice feature of this loan is that interest is accumulating over those periods that you are not making payments. The effect of accumulating interest cost is that the principal loan balance is increasing—you are in effect borrowing to pay the interest costs on your loan.
Example 17.7. Borrowing to learn. Suppose you obtain a student loan of $12,000 to cover your last year of schooling expenses. No payments are required during your last year in school. After graduation you are required to repay the loan plus accumulated interest over 3 years of monthly payments. Assume the market interest rate is 7.5% which is the interest rate charged on your student loan. What is the NPV of this loan. What is the effective rate on the loan? The timeline for this loan is described in Figure 17.1.
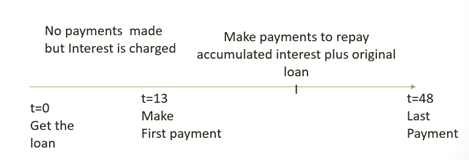
Step 1 for analyzing the skip payment loan is to find the payment A to be made over three years beginning 13 months after the loan was obtained. The amount of the loan to be repaid beginning in month t = 13 is $12,000(1.075), the original amount plus interest charges. This amount must be repaid with 36 payments at an interest rate of 7.5%/12 = 0.625%. What makes the solution to this loan interesting is that we are finding the solution as though we were standing at time period t = 13 where the amount to be repaid equals the discounted value of payments at the beginning of of loan month 13 or the end of loan month 12. We describe the solution using an Excel spreadsheet:
| B4 | fx | =PMT(B1/B2,B2*B3,B5,,0) | |
| A | B | C | |
| 1 | rate | 0.075 | |
| 2 | m | 12 | |
| 3 | n | 3 | |
| 4 | pmt | ($401.27) | =PMT(rate/m,m*n,PV,,0) |
| 5 | PV | $12,900.00 | $12,900 = 1.075 * $12,000 |
Our calculations find that to repay a one-year skip payment loan to be repaid over three years of monthly payments at an interest rate of 7.5% is equal to $401.27. We may be interested in what would have been the loan payment if repaid over four years—without one year of skipped payments? Resolving our Excel payment problem by replacing PV of $12,000 with $12,900 and n = 3 with n = 4, we find:
| B4 | fx | =PMT(B1/B2,B2*B3,B5,,0) | |
| A | B | C | |
| 1 | rate | 0.075 | |
| 2 | m | 12 | |
| 3 | n | 4 | |
| 4 | pmt | ($290.15) | =PMT(rate/m,m*n,PV,,0) |
| 5 | PV | $12,000.00 | |
Skipping one year of payments led to an increase payment from $290.15 to $401.27. Was the immediate increase in liquidity equal to the decreased liquidity over the three years of repayment? We can’t answer that question, the best financial managers can do is describe the consequences of one’s financial choices.
Finally, we ask: what is the difference between the effective interest rate on the old and new loan? There is no difference, None! Can you explain why? For the same reason that we don’t change NPVs when we reinvestment and discount at the same interest rate. Acquiring a skip payment loan at the market interest rate may increase future cash flow obligations, but it doesn’t change the NPV of the loan.
Disguised Interest Rate Loans
One of the challenges financial managers face when considering borrowing decisions is knowing the actual cost of borrowing—or, stated another way, knowing the effective APR interest rate. Sometimes lenders offer loans that disguise the real cost of their loans. We call loans with disguised interest rates, disguised interest rate loans.
Disguised interest rate loans have effective interest rates than are presented in the loan description. For example, interest costs can be subtracted in the initial period, reducing the actual loan amount received by the borrower (a discount loan). Interest can be charged as though the original loan balance was outstanding throughout the life of the loan (an add-on loan). Alternatively, the lender can charge a loan closing fee, reducing the actual loan balance received by the borrower. Additionally, the interest can compound more frequently than loan payments occur. Each of these methods will increase the effective interest rate above the stated interest rate. Consider several types of disguised interest rate loans.
Discount loan. A borrower approaches his lender for a loan of L0 for mn periods. The borrower learns that the stated interest rate or disguised interest rate is rd. When the borrower picks up the check for his loan, the amount he receives equals only:
(17.15) ![]()
the amount of the loan requested less the stated interest rate times the term of the loan. Meanwhile, the constant loan payment is calculated as:
(17.16) ![]()
To calculate the APR associated with this loan, treat payments of amount A as if they were associated with a constant payment loan that retires a principal of L0.
Example 17.8. The effective interest rate for a discount loan. To illustrate the discount loan, assume a consumer obtains an installment loan for $10,000, from which $2,500 is deducted for interest costs. The loan is to be repaid over 2 years, with monthly payments equal to $416.67 = ($10,000/24). To solve this problem and find the effective interest rate, we key into our Excel RATE function:
(17.17) ![]()
Displayed is the actuarial monthly rate of 2.44% or, after multiplying by 12, we find the corresponding APR rate of 29.3%. The effective rate re is: re = (1.0244)12 – 1 = 33.55%.
This is quite a difference compared to the stated interest rate of 12.5%. Hence, the discount loan effectively disguises its true APR.
Discounts for on-time payments. Sometimes disguised interest rates can provide opportunities for significant savings. One such opportunity is discounts offered for on-time savings. You may make a purchase on account and be offered a discount for early payment. For example, suppose you are offered a 2% discount if you pay your bill by the 10th day of the month. After 30 days, interest is charged on your account at the rate of 12% per year so by paying early you give up 20 days of free credit. In other words, you are asked to forfeit 20 days of free credit for a discount of 2%.
What is the effective interest rate you would earn by paying your bill by the 10th of the month? The solution requires that we convert the 2% discount to an annual rate by equating 2% is to 20 days as x% is to 365 days.
(17.18) ![]()
Then solving for x, we find:
(17.19) ![]()
And an interest rate of 36.5% for funds paid on time is really an impressive investment.
Points added loans. Earlier we discussed points added to close a loan when refinancing. Now we discuss points added loans in a different view. We ask: what do points added to a loan do to the effective interest rate? In this case, suppose you are quoted an interest rate of r% for a loan amount of L0 to be repaid over mn periods—and then just before you sign, you are informed that there are p points changed to close the loan adding a transaction charge of pL0 to obtain the loan. To find the effective rate we simply compare the rate without the refinancing cost with the rate associated with the rate.
For this example, we continue with the loan described in Table 17.8 of $8,000 for monthly payments over 5 years at 1%. The payment for this loan has already been calculated as $136.75. Now suppose that the lender requires an 8% closing fee to close the loan of 8% * $8,000 = $640. In effect what points required to close a loan means that the actual loan amount available to the borrow is reduced by the closing fee, in this case $640 so that the actual loan is $7,460 rather than $8,000. To find the rate associated with the point added loan we employ the Excel Rate function and find:
(17.20) ![]()
Then multiplying the actuarial rate by 12 to find the new APR: 12 * .3175 = 3.8% so that adding points to a loan more than doubled its effective interest rate from 1% to 3.8%.
Future Values
Up until now, we have emphasized the importance of converting future cash flow to their equivalent worth in the present. Hence, the title to this book includes the words, present value. On the other hand, there are times when values in the future deserve our focus. One future focus may be an anticipated event such a future purchase that requires an accumulation of funds and interest. For example, suppose that one anticipates a large capital purchase such as a house or machinery. Or one may be interested in having sufficient funds to generate an annuity at the time of retirement. We represent a future value at the beginning of period n as FVn.
Example 17.9. Saving for a down payment. Suppose you want to buy a house for $200,000, but to obtain a loan, you must pay a down payment of 10% or $20,000. If you intend to save a monthly amount for 3 years which you reinvest at 5%—what is the amount you must save? To answer this question, we need to distinguish between two different kinds of annuities. Annuities due are annuities paid at the beginning of the period (type = 1 in Excel’s PMT function). Ordinary annuities are paid at the end of the period (type = 0 in Excel’s PMT function). Knowing when payments (annuities) are paid, at the beginning or end of the period, is important when making payments to achieve some future financial goal.
So, we want to find what amount must we save and invest for 36 monthly payments that earn 5% APR such that their compounded accumulations at the beginning of period n + 1 will equal the $20,000 required for a down payment for a future capital purchase? Suppose you make payments at the beginning of n period so that at the beginning of the n + 1 period or the end of the nth period you have available a future value of FVn+1 equal to:
(17.21) ![]()
| B6 | fx | =PMT(B1/B2,B2*B3,,20000,1) | |
| A | B | C | |
| 1 | rate | 0.05 | |
| 2 | m | 12 | |
| 3 | n | 3 | |
| 4 | nper | 36 | =(m*n) if type = 1 |
| 5 | rate/m | 0.41% | |
| 6 | pmt | ($513.94) | =PMT(rate/m,m*n,PV=0,FV,type=1) |
| 7 | FV | $20,000.00 | |
Alternatively, we could find the 36 monthly payments required if the payments were made at the end of each period that compound at an APR of 5% APR so that at the beginning of the nth period the accumulated savings will equal $20,000.
(17.22) ![]()
| B6 | fx | =PMT(B1/B2,B2*B3,,20000,0) | |
| A | B | C | |
| 1 | rate | 0.05 | |
| 2 | m | 12 | |
| 3 | n | 3 | |
| 4 | nper | 35 | =(m*n)-1 if type = 0 |
| 5 | rate/m | 0.41% | |
| 6 | pmt | ($516.08) | =PMT(rate/m,m*n,PV=0,FV,type=0) |
| 7 | FV | $20,000.00 | |
Summary and Conclusions
In this chapter we demonstrated the versatility of PV models by using them to analyze loans. For constant payment loans, we used PV models to solve for constant loan payments, terms, loan amounts, and interest rates—remembering that one PV equation can solve for at most one unknown.
Using PV models to analyze loans required that we identify the various kinds of interest rates. This was an important exercise because we discovered the difference between stated interest rates and effective interest rates—the interest rate actually paid on the loan funds made available.
Another important exercise was discovering the sensitivity of the relationship between the size of the loan payment and the term of the loan. In most cases, the relationship is not one-to-one. In other words, a 1% increase in the size of the loan payment rarely leads to a 1% drop in the term. The corresponding percent decline in the term of the loan is usually much, much more. Hence, we discovered that, when applying for loans, it pays to explore various terms and sizes of loan payments and find the best match—the one with the optimal trade-off between term and liquidity.
A common problem is that existing loans often need to be refinanced. Such may be the case when interest rates drop or a project currently financed is expanded and additional funds are required. In the text we considered refinancing existing loans and found break-even loan closing points. In the supplemental materials at the end of this chapter, we will find the more general formula for refinancing when the term, interest rate, and size of the new loan may be different than on the existing loan.
Lastly, we demonstrated how some loans may disguise the true interest rate. While we only illustrated the solution for the discount loan and the points-added loan, there are several other kinds of loans that disguise the true interest rate.
Questions
- Which would you prefer to earn on your savings? An APR rate of 12.5% or a 1% actuarial rate compounded monthly? Given an APR of r percent, what is the most that the effective rate can earn above the APR rate if it is compounded continuously?
- Consider a loan of $80,000 at an APR of 13%. What is the loan payment that would retire the loan if repaid in monthly payments for 10 years? If repaid in monthly installments for 9 years? Compare the percentage change in the term versus the percentage change in the loan payment (the arc elasticity). Finally, find the point elasticity E(n,A) on the original loan.
- Assume a loan of $54,000 with a remaining term of 21 years. The existing loan requires monthly payments at an APR of 11.25%. For a 3% closing fee, the borrowers could refinance their loan at an APR rate of 10% for the same term. What is the effective interest rate on the new loan? What are the break-even points for refinancing the loan? What is the total interest paid on the two loans?
- A consumer obtains an installment loan of $12,000 from which $2,700 is deducted for interest costs. The loan is to be repaid over two years with monthly payments equal to $500 ($12,000/24). Please determine the effective interest rate re on this loan.
- A farm supply store offers its customers 30 days same-as-cash arrangements. That is, for bills paid within 30 days after purchases are made, no interest is charged. On the other hand, to encourage early payments, the supply store offers a 2% discount on bills paid with 10 days. Please calculate the effective interest rate the store offers its buyers for giving up 20 days of free credit.
- Suppose you borrowed $5,000 for 3 years at an APR rate of 8%. Create an amortization table for this loan.
- Home Depot mailed to some of its customers a coupon entitling them to either a 10% discount on their next purchase or two years of free credit. Under what conditions would you be indifferent between the two options? (Hint: the answer does not depend on the amount purchased.)
- A farm firm has a mortgage loan for $150,000 at an APR rate of 5%. The term of the loan is 15 years and the payments equal $14,451. Cash flow problems from reduced farm income leaves the firm only able to pay $10,000 on this loan. What would the new term equal if the lender allowed the borrower to repay over a longer term?
- Some of the material in this chapter was adapted from Robison, L.J. and P.J. Barry (1996); Present Value Models and Investment Analysis. "Chapter 12: Loan Analysis". MSU Press, East Lansing, Michigan. ↵

