Learning goals. At the end of this chapter, you should be able to: (1) explain why unambiguous rankings require one-dimensional measures; (2) understand why consistent rankings require homogeneous measures; and (3) describe present value (PV) model dimensions that require homogeneous measures.

Learning objectives. To achieve your learning goals, you should complete the following objectives:

• Understand the need for one dimensional ranking criterion.
• Evaluate and distinguish between one-dimensional net present value (NPV) and internal rate of return (IRR) ranking measures.
• Learn about PV model homogeneous measures that are required for consistent NPV and IRR rankings that include:
  • homogeneous funding sources;
  • homogeneous initial and periodic sizes;
  • homogeneous terms;
  • homogeneous tax rates; and
  • homogeneous liquidity and currency.

Introduction

Financial managers must decide whether to continue their commitment to an existing investment called a defender or disinvest in the defender and commit resources to a new investment called a challenger. More complicated investment problems may require that we choose between a defender and several challengers—mutually exclusive challengers, challengers that can be acquired in combination with other challengers, and time sequenced challengers. To describe the nature of defenders and challengers and the need for homogeneous measures, we introduce a simple one-period present value (PV) model.

Suppose we have already committed V₀^d to a defending investment in exchange for its future cash flow equal to R₁^d. Now suppose that the rate (1 + r^d) at which the defender exchanges present and future dollars is:

(12.1)  

Now consider an alternative challenging investment. The rate at which the challenger’s investment funds V₀^c are exchanged for future cash flow R₁^c is:

(12.2)  

In equations (12.1) and (12.2), r^c and r^d equal the defender’s and challenger’s internal rates of return. We cannot really say much about the relative internal rates of returns of the defender and challenger unless we require that the two investment amounts V₀^d and V₀^c are equal. If the investment amounts are equal and if (R₁^c > R₁^d), then we can make a definitive statement about their relative IRRs, (r^c > r^d).

Now suppose that we equate r^c = r^d + α  and rewrite equation (12.2) as:

(12.3)  

Finally, we divide both sides of equation (12.3) by (1 + r^d) and write:

(12.4)  

where the present value of earnings, αV₀ / (1 + r^d), will be referred to net present value, NPV.

Opportunity Costs

An opportunity cost is a benefit, profit, or value of something that must be given up in order to acquire or achieve something else. An economic couplet declares that there is no free lunch. If you want lunch, you must pay for it—sacrifice something to obtain it. The opportunity cost, the cost of lunch, of investing in a challenger is the IRR of the defender. NPVs measure the difference in the present value of future earnings if the investor sacrificed the defender to invest in the challenger.

Prices are not opportunity costs. The price of a good is the amount of money, or money equivalent, paid to obtain it. The amount of money or money equivalent paid to obtain the good represents the direct cost of what is given up to acquiring something desired or to avoid something disliked. However, there may be other costs incurred to acquire a good—or to avoid a bad—besides the price paid. For example, one might consider the cost of attending a movie to be the price of the ticket. However, transportation costs to and from the theater could add to the actual value of what must be exchanged to attend the movie. And there may be other costs of attending the movie such as lost earnings as a result of missing work. Or, suppose the movie was playing while the moviegoer ate his or her prepaid dinner meal. Now the cost of the movie includes not only the price of the ticket plus transportation costs and lost wages but also the value of the skipped meal. The cost of the ticket, transportation costs, lost wages, and the skipped meal together represent the opportunity cost of attending the movie, which is different from the price of the movie ticket.

Opportunity costs and perfect capital markets. The capital (or financial) market is where people trade today’s present dollars for future dollars and vice versa. In a perfect capital market, dollars trade between adjacent time-periods at the (same) market rate of interest. For a perfect capital market to exist, the following conditions are required: no barriers to entry; no participant can influence the price; transactions are costless to complete; relevant information about the market is widely and freely available; products and services are homogeneous; no distorting taxes exist; and investment possibilities are continuously divisible. Finally, the firm’s opportunity cost of capital is the same regardless of the size or purpose of the amount being borrowed or lent. Finally, in perfect capital markets, investment NPVs are zero.

Though markets for some financial investments are considered highly efficient, they are not perfect. Rates of return on savings rarely equal the rate paid to borrow funds. Moreover, rates of return on investments typically depend on the size and economic lifetime of the investments. Hence, in the real world, investors face imperfect capital markets. We allow for imperfections in capital markets in our PV models by allowing the rate of return on an investment being considered for adoption, a challenger, to differ from the rate of return on an investment that must be sacrificed to adopt the challenger, a defender, to vary. In imperfect markets, the opportunity cost of the defender and the market rates of interest on loans are rarely equal.

One-dimensional Ranking Measures

An analogy. To uniquely rank defending and challenging investments requires a one-dimensional ranking measure. To make this point, that unique investment rankings requires a one-dimensional measure, assume that we determined the winner and loser of a sporting event by several different measures.

To illustrate, suppose that the winner of the Super Bowl football game depended on the following measures: points earned, yards gained, yards earned on the ground divided by the yards earning passing, yards penalized, injuries sustained, and the number of persons viewing the contest. Most football sports fans would agree that the success measures just described matter—but they would also agree that we would be unable to determine who wins and who loses with such multi-dimensional measures unless in some rare event one team dominated in all dimensions. So, we must decide which measure matters most and in the case of football—the measure that matters most is points earned. Hopefully, all other measures are subsumed in the one defining measure.

We rank most investments using one of two one-dimensional measures, NPVs and IRRs. What does it mean that NPVs and IRRs provide one-dimensional measures? It means that they can be represented by a location along a straight line. Consider other details about NPVs and IRRs as ranking measures. NPVs measure the difference between a challenger and a defender described in present value dollars. Positive (negative) NPVs imply that the investors will increase (decrease) their earning by exchanging the defender for the challenger. Percentage rates of return measure the internal rate of return (IRR) of a single investment. Any comparison between defenders and challengers using IRRs will require an IRR be calculated for each investment.

NPV rankings. To rank investments uniquely using NPV measures requires that we reduce their current and future earning to a single number in the same period. Alternatively, we could compare two investments’ future cash flow in each period of their economic lives. Then, we would likely be unable to rank them because one investment may earn more in one period and less in another that a challenging investment. To avoid the indecisiveness of multi-dimension metrics, we convert future cash flow to their present value creating a one-dimensional number that allows us to uniquely rank defender and challenging investments. To reduce future cash flow to equivalent in the present we assume that a challenger’s earnings are reinvested in the defender and earn the defender’s rate of return.

IRR rankings. Alternatively, investments can be ranked by their IRRs, a percent. But to find a percentage to represent the PV model, we treat each periodic cash flow as equally important by converting them to their present value equivalent. We use the word internal to describe the second ranking method because the earnings from the investment are reinvested in the challenger rather than being reinvested in the defending investment. IRRs have two possible interpretations. One, it is the (internal) rate of return earned by the challenger. Or, it is the defender’s IRR that produces an NPV of zero. Of course, if the defender’s IRR produces an NPV of zero, it means that the defender and challenger’s IRR are equal. If the NPV is positive (negative), then the IRR of the challenger is greater than (less than) that of the defender although there may be some strange exceptions.

The idea that future cash flow can be ranked by their NPVs or IRRs may be one of the most important and pervasive concepts in financial management. It is the basis for ranking nearly every investment with future cash flow including physical investments, bonds, stocks, insurance, pension funds, housing, land, cars—and almost anything that has more than one period of economic life generating cash flow.

The problem of IRR and NPV rankings. There is a problem with having IRR and NPV ranking measures. We don’t have just one—one-dimensional ranking number (points earned in a football game). We have two and possibly more. And when we have more than one, one-dimensional ranking measure, we have the possibility for inconsistent rankings. And we do.

IRR and NPV ranking criteria routinely produce inconsistent rankings and provide unlimited opportunities for academics to argue about their relative virtues. And here is the main point of this chapter, if we compare challengers and defenders using homogeneous measures, we can guarantee that IRR and NPV rankings will provide consistent rankings.

Homogeneous Measures

What adds complexity to choosing between a defender and a challenger and among challengers is that they often have different characteristics that make comparisons between and among them difficult. Moreover, these differences between challenging and defending investments, unless addressed, may result in inconsistent rankings. As a result, we may be unsure which is the preferred investment decision. This chapter intends to describe how we can avoid inconsistent investment rankings by requiring homogeneous (same) values for some investment characteristics. We do allow for some investment characteristics to be unequal–the ones that lead us to prefer one investment over another.

What is homogeneity? Homogeneity is the quality or state of being equal or of the same kind. Homogeneity synonyms include uniformity, equality, consistency, and harmony. Employed in our investment ranking discussion, homogeneity means that measures not relevant to the rankings of investments should be equal and not allowed to influence ranking outcomes. Homogeneous measures can be of two kind. We are measuring the same thing, inches, pounds, days of the year, time in the mountain time zone, etc. The second meaning of a homogeneous measure is that the value of the same characteristic being compared is the same across investments.

On the other hand, not all measures used to describe need or should be homogeneous, at least in the second meaning of the word. If all the measures were used to describe defending and challenging investments were homogeneous, they would be the same value and we would not be able to distinguish between investments. To emphasize the need for homogeneous measures, we introduce a horse racing analogy.

An analogy. To make the point that a lack of homogeneous (same) measures may create ranking conflicts, even when the comparisons involve one-dimensional measures, we compare ranking investments to a horse race. We organize horse races so that other factors besides the horses’ speed do not influence the horse race outcome. For example, we expect that only horses enter the race. We require that the horses all begin the race at the same time and place. We expect that all horses will run the same distance and at the same time—that implies that not only has the starting point and time has been determined but the finish line as well. We require the jockey’s weight not be a factor. Finally, we expect that everyone agrees that the criterion for ranking horses is the time interval between when each horse starts and finishes the race.

Ranking investments is, of course, not a horse race. Yet, the process of ranking investments according to their rates of return or earnings and horses according to their speed have many elements in common. First, we assume that we are comparing investments of the same size (only horses run the race). We also assume that we are comparing investments over the same time-period or term, (the length of the race is the same for all horses). Finally, we assume that the criterion used to rank investments (NPVs or IRRs) would provide the same rankings for each investment just as we would agree that timekeepers would agree on which horse crossed the finish line first. For the horse race to be fair, i.e. that the outcome is not influenced by irrelevant factors unrelated to the horses’ speed, we control for as many differences as possible and meaningful. Only when controlling for irrelevant factors can we make the horse’s speed the most important factor, the one nonhomogeneous factor that determines the winner.

To continue our analogy, suppose we wanted to compare the average speed on horses in different races. That may be difficult because so many conditions may not be controlled or made the same between races. Different locations, different conditions and length of the track, different weather conditions and time of day and time of year—all these and others may all influence the speed of the horses in that race. And if those difference between races were not enough to complicate the comparisons, consider the differences between horses: their age, weight, gender, genealogy, races run previously during a set period, their diets, and overall health, how it was trained—to name a few. All these differences may lead us to ask—what can we infer from race outcomes? What we want to know is what variables should not be measured in homogeneous measures? It may be that what we don’t want to make homogeneous is something intangible—the horse’s desire and will to win. Like we meant to say, it can be complicated.

Homogeneous Cash Flow Measures

We have emphasized that for NPV and IRR to provide consistent rankings, defender and challenger investments must be measured in homogeneous units. Perhaps the two most important homogeneous characteristics is that the economic activity of the defender and challenger must be both represented by cash flow. And secondly, the cash flow used to represent the economic activity of the defender and challenger must be measured in common present value units.

The cash flow principle. One investment dimension that both the defender and challenger must adopt to represent their economic activity, is the cash flow it generates and when. We refer to this requirement as the cash flow principle. When building a PV model, we represent economic activities of the firm by their cash flow. In our horse race analogy, the cash flow principle is equivalent to letting only horses run the race. Some activities of the firm produce what we characterize as noncash outcomes such as appreciation (depreciation) of assets, increases in inventories of unsold goods, and increases in accounts receivable and payable. But these events are not included in PV models because they do not produce cash flow.

One justification for the cash flow principle is that, at some point, we expect all economic activities to generate cash flow. At some point, we expect inventories to be liquidated and generate cash. At some point, we expect accounts receivable and accounts payable to be settled for cash. At some point we expect long-term assets that have appreciated (depreciated) to be sold and the difference between their acquisition and sale price to capture the noncash flow of depreciation (appreciation). Thus, in effect, we do count all economic activities of the firm by recognizing only cash flow; however, we count them only when they create cash flow.

The cash flow principle requires that careful distinction be made between a cash transaction and a noncash transaction. Sometimes the distinction is not always clear. For example, an asset’s book value depreciation does not itself generate a cash flow. Depreciation expenses of an investment do, however, generate a tax shield that creates a cash flow in the form of reduced tax payment. Thus, we include the cash flow associated with tax savings resulting from depreciation of an asset but not the depreciation.

Present value equivalent cash flow. We already determined the need for homogenous measures to unambiguously rank investments using either NPVs or IRRs. Furthermore, we earlier accepted that a dollar in the present in not the same as a future dollar. But how do we reconcile that our NPV and IRR models consist of time-dated cash flow that are inherently differ from each other? The answer is that we exchange them with their present value equivalent by discounting them either with at the defender’s or the challenger’s IRR.

Consider a percent that describes the exchange between future dollars (A) and present dollars (B). We exchange future and present dollars every time we lend or borrow money, make or liquidate an investment, or invest in or withdraw money from a retirement account.

To illustrate, suppose I borrow present dollars V₀ now from a lender and in one year from now, I repay the lender future dollars R₁ where the subscript indicates the end of the time-period in which the cash flow occurs. Since the ratio contains numbers of the same units, the rate of exchange between me and a lender is (R₁/V₀) equal to the decimal (1 + r) or as sometime reported, as r percent. We summarize the ratio of future to present dollars expressed as a decimal equal to:

(12.5)  

To illustrate, suppose V₀ equals $100 and R₁ equals $110. In this example the ratio of future to present dollars is: $110/$100 = 1.10 or 110% and we could say that one present dollar can be exchanged for 1.10 future dollars.

Now suppose I want to receive R₁ dollars one period in the future in exchange for V₀ now. The percentage describing the exchange is (V₀/R₁) equal to 1/(1 + r) or if multiplied by 100%, I could say that I can exchange future dollars for present dollars at (1/1 + r) percent.

(12.6)  

To illustrate, suppose V₀ equals $100 and R₁ equals $110. In this example the percentage of present to future dollars is $100/$110 = 0.91 and we could say that one future dollar can be exchanged for present dollars at .91 percent. Sometimes we say that one dollar in the future can be discounted to 0.91 present dollars, expressing our ratio as a decimal.

The variable r appears frequently in PV models that describe money exchanged across time. It is important to recognize that r is a decimal. However, when it is used in a ratio or equation with dollars—it is often referred to as a rate. For example, consider equation (12.7).

(12.7)  

In equation (12.7) r is a decimal or percent that multiplies present dollars to find future dollars and we refer to it as the rate of return earned on initial investment V₀.

Exchanging present dollars for a future dollar over more than one period. If we know the exchange rate r and are willing to assume it is constant over time, it is a small step to convert present dollars to their equivalent in the future or to convert future dollars to their equivalent in the present. We simply multiply or divide by the appropriate rate. To convert present dollars to their one period in the future value we multiply by (1 + r). To convert future dollars to their present worth, we divide or discount by 1/(1 + r).

To illustrate the importance of calculating the present value of future cash flow, suppose that a “down-on-her-luck friend” approaches you. She explains that her wealthy aunt has promised her $100 in one year, but she needs the money now. She asks you what you would offer in present dollars in return for her future $100 dollars. You quickly calculate (assuming an exchange rate of 110% or 1.10), and report that the present value of $100 future dollars (received in one period from now) is $90.91. Or, we might say that the discounted present value of $100 future dollars is $90.91.

Just as we found the present value of one period in future dollars, we can also find the present value of future cash flows received in two or more periods in the future. Returning to our earlier example, suppose this same down-on-her luck friend offers you R₁ dollars in one period and R₂ dollars two periods in the future and asks how many present dollars would you offer for the exchange if the exchange rate is (1 + r).

We can find the present value of R₂ in two steps. First, convert R₂ to its equivalent value in period one dollars by discounting at the rate of 1/(1 + r) or [R₂/(1 + r)]. Then we discount [R₂/(1 + r)] by dividing again by (1 + r) to convert period one dollars to present period dollars. Important to note is that the exchange rate is assumed to be (1 + r) between any two periods, including between periods one and two. We summarize our two period future cash flow discounted to their present value as:

(12.8)  

We would follow a similar procedure to find the present value of dollars received in three periods from the present. Suppose you were offered $100 for the next three periods. What is the present value of these future cash flows if the exchange rate were 110 percent between any two periods? The answer is:

(12.9)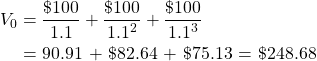  

Homogeneous measures and winning horses. In sum, when comparing horse races and investments, we try and make homogeneous any many irrelevant factors as possible. If we do not, the results will be influenced, biased, by factors we don’t want to determine the outcome. And there is more. Not only do irrelevant non-homogeneous investment dimensions bias rankings, that may also produce inconsistent IRR and NPV rankings. In other words, if we allow to many factors to vary, we may get a decisive race outcome but not be able to determine if it was meaningful. In the remainder of this chapter and in the following chapters, we focus on several investment dimensions that must be measured the same, homogeneously, so that our investment rankings will be unbiased and that NPV and IRR rankings will be consistent.

Other Homogeneous Measures

In what follows, we briefly introduced those investment dimensions that should be made homogeneous to produce consistent NPV and IRR rankings. Later, each dimension will be emphasized in a separate chapter. We have already noted that PV models should measure economic activity using only cash flow and convert them to their present value equivalent. We also described in Chapter 8 the need to measure earnings and rates of return from either assets or equity. We should also compare investments of the same initial and periodic sizes, terms, tax codes, and liquidity and currency.

PV models are designed to measure time-dated cash flow in homogeneous units by converting them to their equivalent present value. This is key and fortunately is inherent in PV models. But there are other investment dimensions besides their time dated cash flow that may not only be measured in different units but may be measured in the same weight but given different values. As a result, investments not measured in homogeneous unit may produce inconsistent IRR and NPV rankings. We describe these next and they are so important that in what follows we devote a separate chapter to each measure.

Homogeneous funding sources. An important characteristic of an investment that should be homogeneous across investments being compared is the investment’s funding source. This topic is covered in Chapter 8, but homogeneous funding sources is not the only focus of chapter 8. Homogeneity of investment funding requires that both defenders and challengers must attribute their earning and rates of return to either its equity or assets. To be specific, if two investments are being ranked using their IRRs, then cash flow for the investments must be either attributed to cash flow from equity or assets. If two or more investments are being ranked using NPVs, then cash flow for challengers and the defender’s discount rate must be attributed to either equity or assets. To avoid confusion, we will describe the rate of return on equity as ROE or IRR^E. And we will describe the return to the firm’s assets or investment as ROA or IRR^A. If we wish to compare earnings on the investment or assets, we will compare NPV^A. If we wish to compare earnings on equity, we will compare NPV^E for the different investments.

So how do we build PV models that measure earnings and rates of return on assets or equity? When finding the ROA for the defender, we ignore cash flow that includes borrowing or lending activities. The advantage of this approach is that it measures the rate of return on assets independent of the returns from the loan used to finance the investment. We write the defender’s cash flow and its corresponding IRR that measures ROA as:

(12.10)  

where V₀ is the initial investment, R₁ is net cash flow earned in the first period, and S₁ is the liquidation value of the investment after one period. Then we write the ROA as:

(12.11)  

Interpreted, equation (12.11) equates ROA to cash returns R₁ including cash value of capital gains (losses) equal to the difference between the liquidation value and the beginning value of the asset all divided by the beginning value of the assets. It measures the rate of return on the firm’s assets including returns generated by human capital, manufactured capital, social capital, natural capital, and financial capital.

In this approach, we do not account for the source of funding for the investment—equity or assets. Unless otherwise specified, it includes both debt and equity funding. In this calculation, we do not charge for interest costs charged on debt capital because the entire investment is charged at the beginning of the investment cycle and to charge for interest costs would double count the cost of using debt capital.

To measure the rate of return on the firm’s equity, we only charge for equity initially invested and charge principal and interest payment in the time period they are repaid and the loan balance and the end of the analysis. In this formulation we net out the cost of using debt capital and attribute the remaining earnings to invested equity.

To calculate returns to earning by subtracting out the use of debt, assume that an asset is acquired using debt D₀ plus equity E₀ whose sum is equal to V₀. At the beginning of the project, the firm supplies equity capital to purchase the investment creating a negative cash flow of E₀ dollars in the beginning period.

Then it receives D₀ from the lender and pays D₀ to the seller to complete the purchase of the investment. Since the investor receives D₀ from the lender and pays debt capital D₀ to the seller of the asset at the beginning of the period, they cancel out making net cash flow from debt capital at the beginning of the investment zero. At the end of the period, the investment repays debt capital D₀ plus interest iD₀ to the lender. In a one period model, the investor pays back to the lender, debt capital D₀. Thus, we can express these cash flow as:

(12.12)  

And we can write the ROE as follows:

(12.13)  

We are interested in the relationship between ROA and ROE. To determine that relationship, we first solve for R₁ in equation (12.11) and find that it equals:

(12.14)  

Then we make the substitution for R₁ in equation (12.13) using equation (12.14) and replacing V₀ with (D₀ + E₀) we again the rates of return identity (RORI) result:

(12.15)  

What equation (12.15) reveals is that ROE > ROA as long as the firm earns a positive return on its debt capital (ROA > i).

Homogeneous initial and periodic investment sizes. Homogeneous size measures (Chapter 13) require that initial and periodic investment sizes for challengers and defenders must be equal. This seems like an obvious requirement. Nevertheless, it is routinely ignored and often produces conflicting NPV and IRR rankings. To apply the homogeneity of size requirements, initial investment differences must be resolved. We resolve initial size difference by accounting for their earnings especially that remain invested in a defender. Periodic cash flow in PV models represent investment withdrawal that alter the size of the investment. To maintain periodic size homogeneity, cash flow is compounded until a common ending period.

Our goal is to obtain unbiased investment and cash flow measures. This requires not only homogeneous measures but that all cash costs and cash returns associated with an investment should be included when determining an investment’s present value. Consider how the total costs and returns principle is applied in several practical situations. Whenever low-interest loans or preferential tax treatments are tied to the ownership of a durable, these concessions will influence the present value of the investment. To ignore these benefits (costs) would lead to an under or over evaluation of the worth of the investment.

Sometimes an investment such as land has more than one source of returns. Mineral deposits, potential recreational use, and urbanization pressures may create expected returns over and above those associated with agricultural use. Pollution standards may impose costs in addition to those normally experienced. All these expected cash costs and returns that influence the value of the durable should be included in the PV model. And cash flow associated with decreased accounts and inventories should also be included.

Requiring initial and periodic size equality is analogous requiring horses in the same race to be of the same size.

Homogeneous terms. Just as we would expect horses in the same race to run the distance, we would expect that investments being compared would be measured over the same term. Chapter 14 describes how we implement the homogeneity of term requirement. Similar to the method used when satisfying the homogeneity of size condition, when comparing investments of two different terms, we must account for the investments’ earning between the term of their investments.

Complicating the application of the homogeneity of term requirement are sequenced investments, one s that cannot occur without a similar disinvestment. For example, we cannot invest in a new orchard or cohort of animals without deciding the term of the existing investments.

Homogeneous tax rates. Taxes represent withdrawal from the firm’s earning by government. Homogeneous tax-rate measures (Chapter 15) require that we account for differences in effective tax rates for defenders and challengers that depend on cash flow patterns and capital gains (loses). The main point here, is that tax considerations should be equally considered when evaluating the challenger as well as the defender. On the other hand, some taxes may not be identically applied to both defenders and challengers and require a careful consideration of the effects of taxes.

Homogeneous liquidity and currency measures. Homogeneous liquidity measures (Chapter 16) recognize that firms and investments can be differentiated by their liquidity. This is a difficult concept to apply when ranking investments. And perhaps the best we can offer is to provide liquidity measures that differ by investment types.

A different homogeneity measure applies why engaged in global trade across countries and currencies. Now the rate of currency exchange becomes and important consideration and even more so when it varies over time.

Summary and Conclusions

The discount rate in a PV model represents the defender’s IRR. It is the rate of return sacrificed by disinvesting in the defender to acquire the challenger. The defender’s rate of return measures either its ROA or ROE. Choosing the appropriate discount rate for NPV models describing a challenger is perhaps the most difficult task of investment analysis. The choice essentially involves the identification of challengers and opportunity costs associated with defenders.

When ranking investments, we have available one of two possible one-dimensional ranking criterion, NPVs or IRRs. Ideally, these should provide consistent rankings regardless of whatever method we use. Unfortunately, this is not always the case and to be true in general requires that we adopt homogeneous measures for describing challenging and defending investments. These homogeneous measures are so important that they occupy much our effort in chapters 13, 14, 15 and 16 that follow. Our goal is that by using homogeneous measures to construct PV models we can obtain consistent, stable, and accurate investment ranking. Knowing that one’s investment rankings are stable, accurate, and consistent is essential for the success of a financial manager whose goal is to maximize the present value of the firm’s investments.

Questions

1. The fundamental concept of PV analysis is that a dollar today is not valued the same as a dollar received in the future. List several reasons that might explain why a dollar today may not be valued the same as a dollar in the future.
2. The idea that the value of a good today is not the same as the value of the good in the future is a universal concept. Suppose you were offered a 2020 Ford F-150 pickup truck for delivery today or the same truck in the same condition delivered in 2023. If the price today for the truck were $40,000, what would you offer today for the truck to be delivered in 2023? If the prices you would offer are different, please explain why?
3. Explain the importance of valuing future cash flow in one single period, e.g., the present period.
4. Explain the difference between ratios, percentages, and rates.
5. To test your understanding of exchange rate between present and future dollars, please answer the following. Suppose that you could exchange one apple for 1.1 oranges. What is the exchange rate between apples and oranges, between oranges and apples? Compare the exchange rates between apples and oranges and oranges to apple to the exchange between present and future dollars is r=.1 or 10%.
6. Two important economic concepts associated with PV models and investments in general are price and opportunity costs. Opportunity costs are the sacrifices required to obtain a good. The market price of the good may be part of the opportunity cost, but likely not the entire opportunity cost. Consider the opportunity cost of attending the university. These may include income sacrificed. Then compare the opportunity cost of attending the university with the tuition costs, a direct cost. Describe the differences between opportunity costs versus direct costs in other personal activities.
7. Suppose that you invest $100 today. Then assume that one year later your investment returns $110 in cash. Assume that your opportunity cost of capital is 12%.
   1. What is the NPV of the investment?
   2. What is the IRR of the investment?
   3. What is the ratio that converts dollars received one period in the future to their present value?
   4. What is the ratio that converts present dollars to their value one period in the future?
8. A financial manager believes that a defending investment can earn $500 for the next six years. He also believes that his defending investment can be sold today for $2,500. What is the opportunity cost of sacrificing the defender to invest in a challenger? In other words, find the IRR of the defending investment.
9. Briefly distinguish between a defending and a challenging investment. Suppose you are considering replacing an outdated piece of equipment with two different pieces of equipment of difference sizes, efficiency, and useful life. In addition, one company offers financing while the other one assumes buyers will provide their own financing. Describe the challenging you might face comparing and deciding between the two investments.
10. In practice, financial managers face more complicated investment problems than deciding between a single defender and a single challenger. Describe how you might solve an investment problem with more than one challenger? One challenger but more than one defender? When choosing between multiple defenders, what would be the appropriate criterion for the preferred defender? How would you analyze a problem consisting of multiple challengers and defenders? What principle from micro economic theory might guide you in preparing your answer?
11. Describe the fundamental different between rates of return and earnings on assets versus equity. Can you think of different considers when earnings and rates of return on assets would be the preferred measures versus conditions when earnings and rates of return on equity would be the preferred measure?
12. Explain how violating homogeneity of size may lead to inconsistent NPV and IRR rankings. (Hint: how do rankings based on a percent (IRRs) versus rankings based on dollar amounts (NPV) permit inconsistent rankings when initial investment sizes are different.)
13. Compare investments of different terms to two horses running a race of different lengths.
14. Since only death and taxes remain a constant, explain why it is important to measure a defender’s and challenger’s cash flow in both before and after-taxes. Suppose that the before and after-tax rankings were inconsistent, what would you conclude. Would you base your investment decision on before or after-tax results?
15. Suppose that you make a significant investment in U.S. currency in a foreign country factory that produces products that are sold and denominated in the currency of the host country? Homogeneous measures require that the investment be evaluated in the same currency. How would you convert a foreign currency to U.S. dollars?