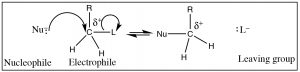In Chapter 1, we learned about one of the most fundamental reactions in organic chemistry: nucleophilic substitution. Before we move on, it is important to make sure that you have a good understanding of what the terms nucleophile, electrophile, and leaving group mean and that you are able to predict the products for a range of substrate molecules (electrophiles) with different leaving groups and nucleophiles. In this section, we move forward and look at nucleophilic substitution reactions in more detail by examining the evidence that leads us to understand how the mechanisms of nucleophilic substitutions were determined.

Kinetics and Mechanisms:

One of the most powerful sources of evidence for how a particular reaction proceeds comes from the study of reaction rates or reaction kinetics. In such studies, how the rate of a reaction changes^[1] is measured as a function of the concentration of each reactant. One of the most common ways of measuring this change is by using a spectroscopic technique. For example, if the compound absorbs in the UV-VIS region of the spectrum, the absorbance is proportional to the concentration. Therefore, if the concentration of the substance changes, it can be measured by changes in the absorbance. The reaction is carried out several times with all but one of the reactants set as constant; then a different concentration of the remaining reactant is added and the rate of the reaction measured. This is repeated for each reactant over several concentrations. The end result of such a study is to produce what is known as the rate equation; for a generic reaction A + B [latex]\rightarrow[/latex] C + D the rate equation takes the form:

Rate = k[A]^x[B]^y

In this equation, k is the rate constant, and the exponents x and y tell us about how the concentration of each reactant influences the rate. The sum of the exponents (that is, x + y + …) is the order of the reaction. For example, if x = 1, then the rate is directly related to the concentration of A. If both x and y = 1, then the rate is directly proportional to both [A] and [B], and the overall reaction order is = 2. If an exponent = 0 then the rate is not dependent on that reactant concentration, and that reactant can be removed from the rate law equation (since [n]⁰ =1 no matter what the value of concentration of n is).

The most important idea to remember is that the rate equation only contains the reactants that are involved in the rate-determining step (that is, the slowest step) of the reaction. If the reaction proceeds by a number of steps, then the step with the highest activation energy will be rate-determining, and only those reactants that participate in this step will be present in the rate law.^[2] Since the rate law is determined empirically, the rate law provides us with evidence about the mechanism of the reaction.

Evidence for the S_N2 Mechanism:

The reaction we discussed earlier in the course is known as an S_N2 reaction that is shorthand for Substitution, Nucleophilic, Second order. We proposed a mechanism for this reaction without providing any empirical evidence, but now let us use some of what you have learned to consider more carefully the evidence for this mechanism.

The reaction is second order: the first piece of evidence comes from the kinetic rate law. The rate of reaction depends on both the concentration of the substrate and the nucleophile: rate = k[RX][Nu]. This means that both must be present in the rate-determining step. 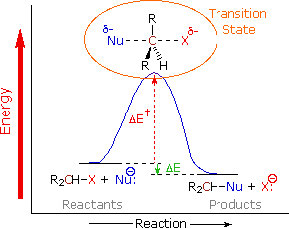The simplest explanation that is consistent with this finding is the one we have already proposed: the nucleophile attacks the electrophilic carbon at the same time as the leaving group leaves. That is, the reaction takes place in one continuous step. A reaction energy diagram in which we plot Energy v reaction progress looks like this (→). In this reaction, there is only one energy barrier, only one maximum in the reaction pathway. The energy of this barrier is known as the activation energy ΔE‡. Looking at the reaction diagram, we also note that the reaction is exothermic (or exergonic if we plot Gibbs energy), since the ΔE of the overall reaction is negative). The species at the peak of the activation energy barrier is known as the transition state, and its structure and associated energy determines the rate of the reaction.

The structure of the substrate affects the rate: Perhaps you have noticed in our earlier discussions of nucleophilic substitution that the organic substrate was always either a methyl or primary carbon attached to a good leaving group. The reason was that in the reactions we have considered, both the rate and mechanism of reaction is highly dependent on the structure of the substrate. 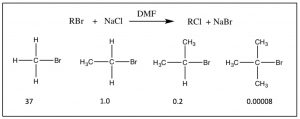As the number of methyl groups attached to the primary carbon increases (from 0 for a methyl group itself to three [tertiary]) the reaction rate slows, as shown. The rate of an S_N2 reaction for a tertiary substrate is negligible.

So two questions arise: first, why are these reaction rates different? and second, why is this change in reaction rates evidence for the S_N2 mechanism? Both can be answered by taking a closer look at the reaction from a molecular perspective. Remember, all of the reactants are dissolved in a solvent; thermal motion leads to their colliding with one another and with solvent molecules. For the nucleophile and the substrate to react with each other, they first have to collide with one another. For a reaction to occur, that collision has to transfer enough energy so that the complex (substrate + nucleophile) can form the transition state—moreover to form the transition-state molecule, the molecules must collide with one another in the correct orientation. Once formed, the transition state can decay to form the products of the reaction.

Recall that our proposed structure for the transition state for this reaction has the central carbon connected to five groups: the incoming nucleophile, the leaving group, and the three other substituents that do not change during the reaction (they are not part of the reaction). As the bond forms between the nucleophile and the substrate carbon, and the bond breaks between the carbon and leaving group, the carbon changes its hybridization state. 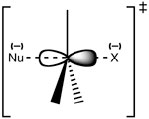What does that mean? In the substrate molecule, the reacting carbon is attached to surrounding groups (H– or CH₃–) with bonds formed from sp3 orbitals. In the transition state, this carbon is still attached to those groups that will remain in the product molecule, but now with bonds formed from sp2 orbitals. Additionally, it is still attached to both the leaving group and the incoming nucleophile using a p orbital to form these partial bonds. You can think of this process as electron density being funneled from the nucleophile through the carbon and out the other side to the leaving group. However, for this to occur the nucleophile can only begin to bond when it approaches from the back of the bond to the leaving group [latex]\rightarrow[/latex].

At this point, you might well find yourself asking: what does all this have to do with the structure of the substrate? For a reaction to occur, the only productive collisions are those where the nucleophile begins to form a bond with the back part of the sp3 hybrid orbital; but the structure of the substrate influences the probability of such an event. In the tertiary substrates (for example (CH₃)₃CBr) the approach to the substrate is hindered by the bulky alkyl groups such that the probability of the nucleophile interacting with the reactive center is low. This phenomenon is called steric hindrance and provides an explanation for the order of reaction of S_N2 reactions.

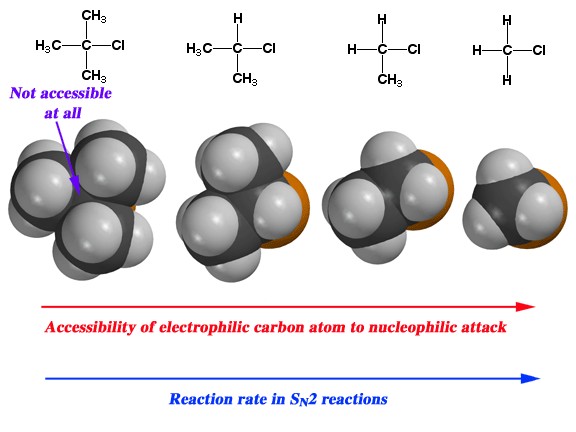
S_N2 reactions at a chiral center: Another piece of evidence for the S_N2 mechanism is what happens

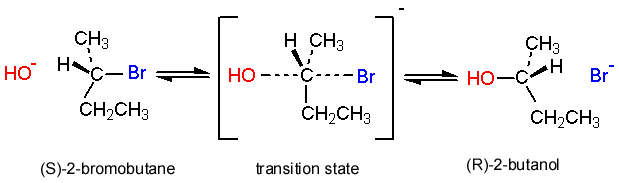when an S_N2 reaction takes place at a chiral center (within a molecule). It turns out that the configuration at that center is changed; the carbon inverts (like an umbrella blowing inside out in the wind) so that an S enantiomer is converted to an R enantiomer. In fact, it is possible to follow the progress of an S_N2 reaction involving a chiral center using a polarimeter (the instrument used to measure optical activity); as the reaction proceeds to completion, the optical rotation of the solution changes over time. For each particular substrate, the direction and magnitude of the rotation for the product will be different. This phenomenon is called the Walden inversion and provides another piece of evidence to support the proposed reaction mechanism.

The role of solvent in an S_N2 reaction: S_N2 reactions are generally carried out in a solvent (why is that?). Empirical studies reveal that such reactions proceed more rapidly when carried out in what is known as a polar aprotic solvent. 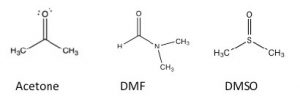So what is a polar aprotic solvent? The term means that the solvent is polar but without acidic protons. Examples of polar aprotic solvents are acetone, dimethyl formamide (DMF), and dimethylsulfoxide (DMSO): each is polar, but lacks a potentially acidic proton such as the H that is bonded to the O in ethanol CH₃CH₂OH or in water H-O-H. Water (and methanol and ethanol) is a polar protic solvent. In a polar aprotic solvent, the negative end of the C=O or S=O dipole is localized to the O, while the positive end is diffuse and delocalized. For example, in acetone, the oxygen has a δ– charge on the oxygen while the positive charge of the dipole is delocalized over both the C and the methyl groups as shown in the electrostatic potential map (→). In practice, polar aprotic solvents can solvate cations well through interactions with the localized negative end of the dipole, but they cannot solvate anions very well. 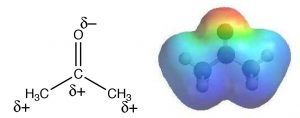Recall that solvation is an interaction that lowers the energy of the system, making it more stable (less reactive). Therefore, a solvent that leaves the nucleophile (the anion) unsolvated will make it more reactive. In contrast, a polar protic solvent (such as water or ethanol) can solvate the nucleophile, through interactions with the positive end of a dipole that is localized on an acidic H, stabilizing the nucleophile and making it less reactive. In summary, S_N2 reactions occur in one step with inversion at a chiral center. Such reactions are generally faster for unhindered substrates and are accelerated when carried out in polar aprotic solvents.

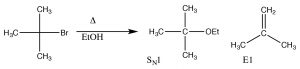
The S_N1 Reaction

If you have already taken a laboratory course in chemistry, you have no doubt observed that you do not get a 100% yield for a particular reaction and often more than one product is generated. This is not (generally) a case of faulty experimental technique, but rather reflects the complexity of reaction systems. Given our experience using evidence to support proposed reaction mechanisms, let us take a look at another set of conditions for nucleophilic substitutions. Consider the reaction:

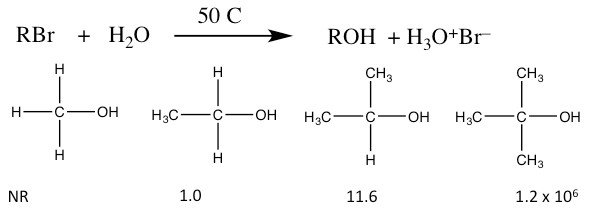
Relative Rates of S_N1 Reactions

In this scenario, water is both the nucleophile and the solvent. Water is not a very strong nucleophile and it is a protic solvent. Under these conditions, a nucleophilic substitution takes place, but this reaction differs in several empirically observable ways from the S_N2 reactions discussed earlier.

1. The rate of reaction depends only on the substrate. The reactivity of the nucleophile is irrelevant. The rate equation for these reactions is: rate = k[RBr]. The reaction is first order, and is therefore named as an S_N1 reaction (Substitution, Nucleophilic, First Order).
2. The relative rates of reaction for substrates are reversed from the S_N2 reaction. That is, reaction rate is higher for the tertiary and lowest for the primary form.
3. When a chiral center undergoes an S_N1 reaction, the product contains a mixture of both possible enantiomers, rather than the inversion of configuration found with S_N2 reactions..
4. The reaction is accelerated by polar protic solvents (which slow S_N2 reactions).

How can we explain these behaviors? Our assumption is that a different reaction mechanism is involved; compared to the S_N2 reactions we have been considering. What might that mechanism be?

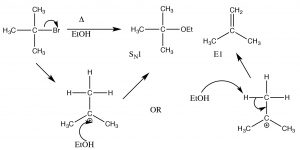
Given that the observed reaction rate is dependent only on the substrate concentration (1) we can assume that only the substrate molecule is involved in the rate-determining step. So how does the reaction begin? We must assume that the reaction involves bond-breaking (since there is nothing else that can happen if there is only one molecule in the rate-determining step. Since bond breaking requires energy, thermal collisions with solvent molecules must drive this bond breaking event. However, we also know that the the solvent molecule does not take part in this step of the reaction (because it is not in the rate law). One possibility is that the bond to the leaving group breaks, resulting in a positively charged carbon (a carbocation) and the leaving group anion [latex]\rightarrow[/latex]. This is the first instance we have seen of a carbocation. The formation of this carbocation requires energy (since the bond is breaking), and we can infer that it has a high activation energy. Carbocations themselves are high-energy species that are very reactive. 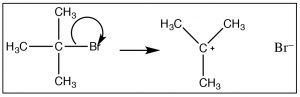However, they are different from transition states in that it is possible to generate and detect the a carbocation—it usually has a short lifetime—but we can detect its presence by spectroscopic methods. This is different from a transition state, which is the highest-energy species on the reaction energy profile. Transition states exist for only one molecular vibration and have lifetimes on the order femtoseconds.

We might expect that such a carbocation would rapidly react with any potential nucleophile present, which in this case is the solvent water molecule.

Although water is a poor nucleophile, it will react with the highly reactive carbocation to give the intermediate protonated form. This is followed by a proton transfer to another water (solvent) molecule to form the final product.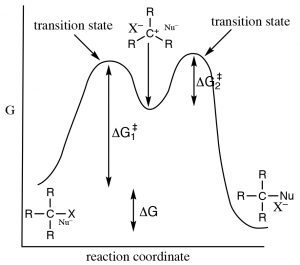

Such a mechanism satisfies our experimental observations. It has a slow (rate limiting, high activation, energy requiring) first step, and a faster (lower activation energy) second step. Because of the differences in the activation energies of the two steps, only the first step is involved in determining the overall reaction rate. To figure out which is the rate determining step we can see that ΔG^‡ for step 1 is larger than ΔG^‡ for step 2.

Why does the structure of the substrate matter? The formation of intermediate carbocation is the rate-determining step in such a reaction, and therefore it follows that the structure of the carbocation has an impact on the activation energy of the reaction, and therefore its rate. The more stable the carbocation, the lower the energy of the transition state leading to the carbocation.^[3] Factors that stabilize the carbocation will also stabilize the transition state and lower the activation energy.

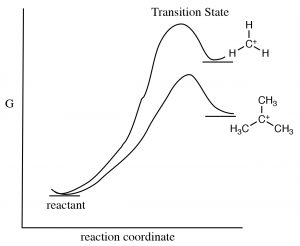There are two mechanisms that can stabilize carbocations and both predict that, as the number of alkyl groups attached to the C+ increase, so will its stability. 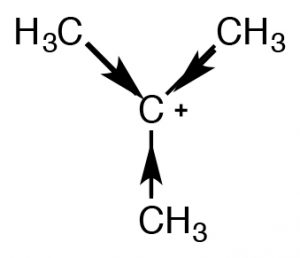One mechanism we have already encountered is induction. The alkyl groups attached to the central carbon, are polarizable and their electron density is attracted towards the positive charge of the central carbon thus delocalizing the positive charge over the alkyl groups. The more alkyl groups attached to the central carbon, the more pronounced this stabilization is. 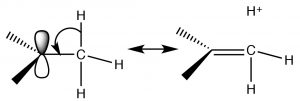The second mechanism, known as hyperconjugation, also delocalizes the positive charge. In hyperconjugation, the electron density from any adjacent C-H or C-C bond can overlap with the empty p orbital on the sp² hybridized carbocation, forming a sort of pi bond and, again, delocalizing the positive charge over the rest of the molecule. The more alkyl groups present (attached to the C+), the more pronounced this effect will be.

Together, both induction and hyperconjugation explain why an S_N1 reaction proceeds faster with tertiary substrates. The tertiary carbocation is more stable (relative to secondary and primary carbocations) so that the reaction has a lower activation energy.

Why do chiral centers racemize? The answer to this question lies in the structure of the carbocation. 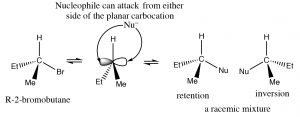It is a planar, sp² hybridized, symmetrical structure. Once formed, it can be attacked from either side by a nucleophile; in simple compounds which side the carbocation will be attacked on involves a random collision event, giving a mixture of enantiomers.

Why are S_N1 reactions accelerated by polar protic solvents? Remember a polar protic solvent (such water or ethanol) contains a dipole: a partially positive and partially negative domain.

Attack at a chiral center gives a racemic mixture of products. 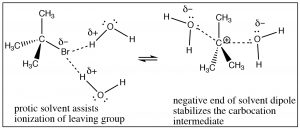This solvent molecule dipole serves two functions: it can solvate the leaving group, in effect helping to remove it from the carbocation through interactions with the positive end of the solvent dipole and it can solvate the carbocation through interactions with the solvent dipole’s negative domain. In essence, the solvent assists in the ionization of the leaving group, and it lowers the energy of the intermediate carbocation.

S_N1 reactions in resonance-stabilized systems: As we have seen, S_N1 reactions tend to occur when a stabilized carbocation intermediate can be formed. 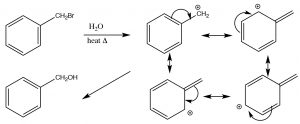In addition to those tertiary cations discussed earlier, which are stabilized by induction and hyperconjugation, there are also occasions when even primary carbocations can be formed if there is a way to stabilize them. For example, any primary carbon that can be conjugated with a pi system can be stabilized by resonance. For example, a benzylic (that is any carbon attached to a benzene ring) carbocation can be stabilized by delocalizing the positive charge into the benzene ring. This lowers the activation energy for the reaction and makes an S_N1 reaction possible.

A similar phenomenon can happen in substrates with leaving groups in the allylic position: 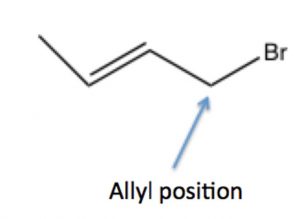that is, on the carbon next to a double bond, where the resulting carbocation can be resonance stabilized by delocalization onto the pi system of the double bond. We will discuss this phenomenon in more detail later (in Chapter 7).

S_N1 or S_N2?

Before we move on, let us review what we know about S_N1 and S_N2 reactions. While it may seem a little confusing, there are a number of factors that can help us predict what the potential mechanism for a reaction might be, and also to predict the product. As we move forward to more complex reaction systems, it will be important to remember that there is typically more than one pathway a reaction can take, but by understanding how reactions occur we can adjust conditions so that the product we want is the major product. The table below summarizes what we have discussed so far with regards to S_N1 and S_N2 reactions.

	SN1	SN2
Substrate	Tertiary>secondary>benzylic~allylic >primary>methyl	Methyl>primary>secondary>tertiary
Leaving Group	Good leaving groups increase rate by lowering the energy of the TS	Good leaving groups increase rate by lowering the energy of the TS Accelerated by strong nucleophiles
Nucleophile	Non-(Bronsted) basic nucleophiles, weak nucleophiles (strong bases promote elimination—see next section)
Solvent	Polar (solvates carbocation) protic (helps pull off the leaving group and solvates it.	Polar aprotic—solvates the cation leaving the nucleophile unsolvated and more reactive.
Stereochemistry	Racemization results from attack at both sides of the planar carbocation	Inversion of configuration if reaction takes place at the chiral center

In practice, tertiary substrates only undergo S_N1 and methyl and primary only undergo S_N2, it is the secondary substrates where the ambiguity lies, and for that we have to consider the other factors such as solvent and nucleophile strength. However, reactions that generate carbocations may also undergo other reaction pathways besides substitution.

Rearrangements: A consequence of generating unstable carbocations

Reactions that generate carbocations can undergo reaction pathways besides substitution.

Consider this reaction:

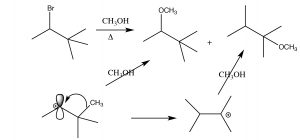
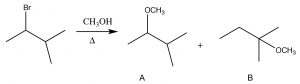The substrate is a secondary alkyl halide, and since the solvent is methanol, a polar protic solvent, and with a weak nucleophile, we would expect an S_N1 reaction to occur, via a carbocation at the secondary carbon. The first product (A) is exactly that, but how did the second product (B) form? To understand this, let us look at the mechanism of the reaction. the first step is the ionization of Br^– to leave behind the secondary carbocation (which produces product A). Product B must have been formed by nucleophilic attack of the O in methanol onto a different carbocation. The precursor to B is a tertiary carbocation, which is more stable than the secondary, and it is formed by what is known as a hydride shift in which the hydrogen shifts with its pair of electrons.

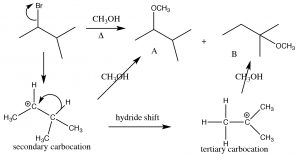
Formation of carbocations is often accompanied by a skeletal rearrangement: Here a 1,2 hydride shift occurs

This rearrangement produces a more stable intermediate that then undergoes reaction; it can also involve the shift of an alkyl group with its electrons from one carbon to the next.

Eliminations

Skeletal rearrangements are a drawback of exposing substrates to conditions in which the leaving group ionizes. Unfortunately, they are not the only complication—there is also the possibility that another type of reaction may occur—an elimination to produce an alkene.

In this case, the reaction proceeds through the same carbocation intermediate, and then a proton is eliminated from a carbon next to the carbocation (a β carbon).

An E1 elimination reaction

This is called an elimination reaction, and it is first-order since the rate-determining step is the formation of the carbocation, and so it is an E1 reaction. In fact, S_N1 reactions are often accompanied by E1 reactions (and vice versa). If there is a possibility of forming more than one alkene (because there are different β carbons), usually the most substituted alkene is the major product.^[4] For example, alcohols undergo E1 eliminations when treated with concentrated sulfuric acid. In this case, there is no substitution product because the sulfate anion is not a good nucleophile (it is highly stabilized by resonance).

Here, the major product has three alkyl groups on the double bond, while the minor product only has two. In fact, this acid catalyzed dehydration of alcohols is quite a synthetically useful reaction, but if the substrate has the potential for rearrangements (i.e. the resulting carbocation can be stabilized by a hydride or alkyl shift), then there is the potential for the formation of even more products. For example:

Elimination and Rearrangements

Obviously, these kind of rearrangements and eliminations are not synthetically useful on substrates that are prone to skeletal rearrangements. However, there is an elimination reaction that typically provides us with much more control.

The E2 Reaction.

As we will see shortly, the synthesis of alkenes by elimination of H–L (where L is a leaving group) is an important reaction, but we are much more likely to have control over the products if the reaction does not go through a carbocation. 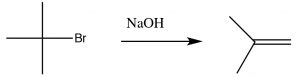That is, if we can simultaneously eliminate both the H⁺ and the leaving group there is less chance of side reactions. This reaction is an E2 reaction (elimination second order), and is promoted by the presence of a strong base. For example, the reaction of t-butyl bromide with hydroxide (or any strong base), shown above. In this case, there is little substitution product, and instead the base simultaneously removes a proton from the β carbon as shown.

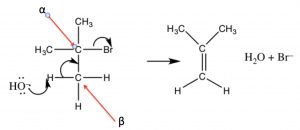An E2 Elimination

The rate therefore depends on both the substrate and the base: Rate =k[RL][base]—that is, a second order reaction. But wait—didn’t we see that strong bases are good nucleophiles? From the beginning, we have shown that methyl and primary substrates with strong nucleophiles undergo S_N2 reactions. How can we bring about an elimination in this case? Well, just as a sterically hindered substrate will not undergo an S_N2 reaction, we can use a sterically hindered base to avoid such reactions. 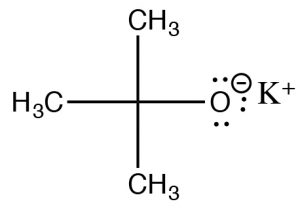If the base is too bulky around its reactive site, then it cannot approach the substrate at the electrophilic center, and will instead pick of a proton from one of the β carbons. One such base is the salt of t-butanol, potassium t-butoxide (tBuOK), which is used to bring about E2 eliminations for primary and secondary substrates.

Just as with E1 reactions, the most substituted double bond is the major product:

Another factor that must be accounted for in E2 reactions is that for such a reaction to occur, 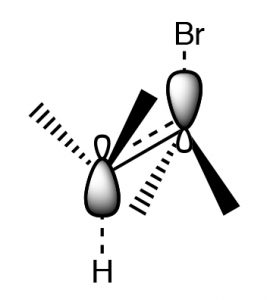the leaving group and the proton that is eliminated must be in an orientation that allows the rehybridizing orbitals to overlap in the transition state.

This orientation is called antiperiplanar, and this need for a specific arrangement for the reaction to occur is called the stereoelectronic requirement.

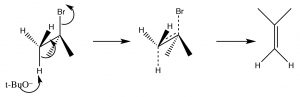
Antiperiplanar (or trans diaxial) stereoelectronic requirement for E2 eliminations

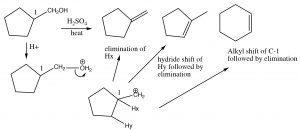
In systems where free rotation is possible, this lining up of the groups is not usually a problem, but if the elimination is to take place in a ring system, then the H and the leaving group must be trans and diaxial, otherwise the stereoelectronic requirement cannot be met.

So, for example, 1-bromo-2-methylcylohexane produces 3-methylcyclohexene, not 1- methylcyclohexene. This is because the hydrogen on the same carbon as the methyl group must be equatorial (if the methyl group is trans). Therefore the axial hydrogen on the other beta carbon is eliminated instead.

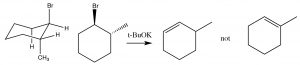
E2 elimination requires a trans diaxial (antiperiplanar) conformation

Nucleophile/base strength	Methyl	Primary	Secondary	Tertiary
Strong/strong e.g. –OCH3	SN2	SN2	E2	E2
Strong/weak e.g. RSH, halide ions	SN2	SN2	SN2	NR
Weak/strong e.g. –OBut, NaH	NR	E2	E2	E2
Weak/weak e.g. H2O, CH3OH	NR	NR	SN1/E1	SN1/E1

One thing is certain: the interplay between substrate and solvent can be very confusing. It is impossibleto memorize all the possible outcomes from a given set of reaction conditions, and although some generalizations can be made, the best way to manage all of this is to try to work through the reaction by writing a plausible mechanism. That being said, the following table summarizes some of the potential outcomes by type of substrate and strength of the nucleophile/base.