Chapter 3: Conformations and Configurations: the consequences of the three- dimensional nature of carbon compounds.
Now it is time to turn our attention to the ways in which the three-dimensional structure of organic molecules affects their stability, reactivity, and the ways in which they interact with one another and with solvent molecules. 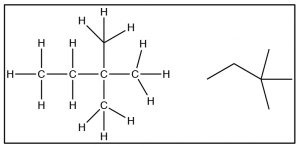 To begin with, we will consider compounds that are composed of sp3 hybridized (i.e. tetrahedral) carbons which are inherently three-dimensional since each of the four bonds points toward the vertex of a tetrahedron (a three-dimensional as opposed to a planar or two-dimensional organization). It is important to remember and understand this aspect of organic chemistry, since we tend to represent organic compounds in ever more simplified (and abstract) two-dimensional diagrams.
To begin with, we will consider compounds that are composed of sp3 hybridized (i.e. tetrahedral) carbons which are inherently three-dimensional since each of the four bonds points toward the vertex of a tetrahedron (a three-dimensional as opposed to a planar or two-dimensional organization). It is important to remember and understand this aspect of organic chemistry, since we tend to represent organic compounds in ever more simplified (and abstract) two-dimensional diagrams. 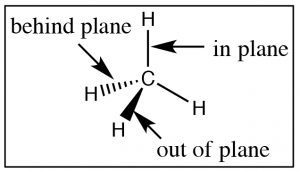 The Lewis structure of a molecule is a 2-D (that is, flat) cartoon that contains a great deal of information (if you know how to look for it). As we move to even more abstracted representations of molecular structures it is easy to forget about the wealth of information encoded within a structural diagram. This includes both how many carbons and hydrogens are present and the three-dimensional relationships between the parts of the molecule. While there are ways to show the three-dimensional nature of sp3 hybridized carbon (such as through the use of wedge-dash structures à), they can be quite cumbersome when it comes time represent complex molecules and we don’t often use them unless we want to specifically address the three-dimensional arrangement of atoms within the molecule. The other idea that gets lost in a static two-dimensional representation is that the bonds between sp3 hybridized carbon atoms are sigma (σ) bonds; the two parts of the molecule linked by a σ bond can rotate relative to each other, without disrupting the overlap between the bonding orbitals.[1] At room temperatures the carbons in most σ bonds are rotating freely and rapidly with respect to each other, although we have to portray them in a fixed orientation when we draw them.
The Lewis structure of a molecule is a 2-D (that is, flat) cartoon that contains a great deal of information (if you know how to look for it). As we move to even more abstracted representations of molecular structures it is easy to forget about the wealth of information encoded within a structural diagram. This includes both how many carbons and hydrogens are present and the three-dimensional relationships between the parts of the molecule. While there are ways to show the three-dimensional nature of sp3 hybridized carbon (such as through the use of wedge-dash structures à), they can be quite cumbersome when it comes time represent complex molecules and we don’t often use them unless we want to specifically address the three-dimensional arrangement of atoms within the molecule. The other idea that gets lost in a static two-dimensional representation is that the bonds between sp3 hybridized carbon atoms are sigma (σ) bonds; the two parts of the molecule linked by a σ bond can rotate relative to each other, without disrupting the overlap between the bonding orbitals.[1] At room temperatures the carbons in most σ bonds are rotating freely and rapidly with respect to each other, although we have to portray them in a fixed orientation when we draw them.
Conformations of Organic Molecules
While most C-C single bonds do allow for free rotation, there are energy costs that are associated with such rotations which arise from the fact that as the carbons rotate around the bond axis, the distance between groups attached to each carbon (even if they are hydrogens) changes. To understand the implications of this changing distance between these groups, recall our previous discussions of London dispersion forces and van der Waals interactions.[2] As two uncharged atoms, molecules, or groups within a molecule approach each other there is initially an attraction between them due to the instantaneous and induced dipoles in their electron clouds (London dispersion forces). 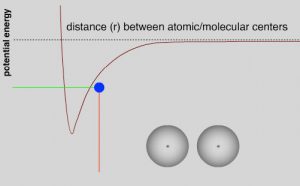 If the molecules (or parts of a molecule) also have a permanent dipole (i.e. the molecule is polar), then there is an additional attractive (or repulsive) interaction in the form of dipole-dipole interactions and hydrogen bonding. Attractive interactions lead to a decrease in the potential energy of the system and repulsive interactions lead to an increase. Even when the interaction is attractive, as the interacting molecules (or regions of molecules) get closer, the repulsive interactions between their electron clouds increase and the potential energy of the system increases. This gives rise to the familiar (or at least it should be familiar) potential energy v distance curve that we have encountered many times in CLUE.
If the molecules (or parts of a molecule) also have a permanent dipole (i.e. the molecule is polar), then there is an additional attractive (or repulsive) interaction in the form of dipole-dipole interactions and hydrogen bonding. Attractive interactions lead to a decrease in the potential energy of the system and repulsive interactions lead to an increase. Even when the interaction is attractive, as the interacting molecules (or regions of molecules) get closer, the repulsive interactions between their electron clouds increase and the potential energy of the system increases. This gives rise to the familiar (or at least it should be familiar) potential energy v distance curve that we have encountered many times in CLUE.
While we have previously discussed this change in potential energy for separate molecules (and atoms), the same principles apply as parts of molecules approach each other, for example, because of rotations around C-C sigma bonds. The different rotational structures of a molecule are called conformations, and one of the best ways to represent different possible conformations is called the Newman projection.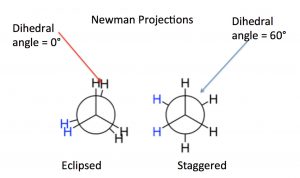 In a Newman representation, we look down the C-C bond of interest; this has the effect of making the groups (atoms, etc.) attached to each carbon (known as substituents) appear to be at angles of 120° to each other (this is due to the perspective from which we are viewing the molecule; the bond angles are still 109°). If we imagine the carbons rotating with respect to one another, we can see how the relative distances between the groups on each carbon change with the “dihedral angle” between the substituents on the front and back carbons. The two conformations shown for ethane are the fully eclipsed conformation, where the dihedral angle is equal to 0°, and the staggered conformation, where the dihedral angle is 60°. As the rotation around the C-C bond continues, these two conformations repeat.
In a Newman representation, we look down the C-C bond of interest; this has the effect of making the groups (atoms, etc.) attached to each carbon (known as substituents) appear to be at angles of 120° to each other (this is due to the perspective from which we are viewing the molecule; the bond angles are still 109°). If we imagine the carbons rotating with respect to one another, we can see how the relative distances between the groups on each carbon change with the “dihedral angle” between the substituents on the front and back carbons. The two conformations shown for ethane are the fully eclipsed conformation, where the dihedral angle is equal to 0°, and the staggered conformation, where the dihedral angle is 60°. As the rotation around the C-C bond continues, these two conformations repeat.
Based on NMR studies at low temperature, these two conformations are not equally stable, the staggered conformation is about 13.8 kJ/mol more stable than the eclipsed conformation. At room temperature, this energy difference is negligible, that is, a typical molecular collision supplies much more energy, and the two conformations rapidly interconvert between one another. As the sample is cooled down, however, the energy available from collisions is reduced (because the molecules are moving more slowly) and we can actually find, based on NMR studies, that we can see different conformations present in different proportions—in part because in the eclipsed conformation the hydrogens on the two carbons come closer to their van der Waals radii and so begin to repel one another, raising the potential energy of the molecule.
Potential Energy v Dihedral Angle for Butane
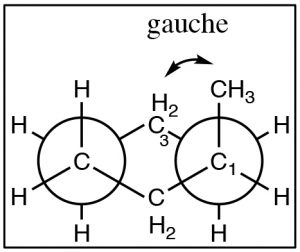
If we look at butane (→) down the C2-C3 bond axis we can see a more exaggerated version of this repulsion due to the presence of the bulkier methyl groups.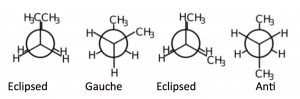 There are two types of eclipsed conformations, and two types of staggered conformations—the anti conformation where the methyl groups are 180° from each other, and the gauche conformation where they are 60° apart. If we plot their relative energies vs dihedral angle we can see how the potential energy changes as the larger centers of electron density (the methyl groups) get closer to one another.
There are two types of eclipsed conformations, and two types of staggered conformations—the anti conformation where the methyl groups are 180° from each other, and the gauche conformation where they are 60° apart. If we plot their relative energies vs dihedral angle we can see how the potential energy changes as the larger centers of electron density (the methyl groups) get closer to one another. 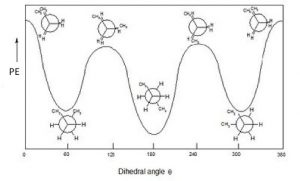 The anti conformation is the most stable and the eclipsed methyl group conformation is the least stable. Again, these energy differences are not all that large. The difference between the highest-energy eclipsed conformation and the lowest-energy anti conformation is about 21 kJ/mole, which is not a big enough barrier to prevent rotation at room temperature.
The anti conformation is the most stable and the eclipsed methyl group conformation is the least stable. Again, these energy differences are not all that large. The difference between the highest-energy eclipsed conformation and the lowest-energy anti conformation is about 21 kJ/mole, which is not a big enough barrier to prevent rotation at room temperature.
By applying these ideas, we can predict conformations of long-chain alkanes as well. We usually draw long-chained alkanes in the most stable (all-“anti”) conformation, but there are occasions when the gauche conformation is also present—the result of this conformation is a bend or kink in the chain.  This has implications how long-chained alkyl groups interact with one another, and influences the molecules’ physical properties, such as melting point. Many biologically-significant lipid molecules contain long-chain alkane groups. For example phospholipids form the structural basis of biological membranes. These lipids are a major component of the cell membrane that is the permeable barrier that surrounds the cell. The long-chain fatty acids that make up the membrane are typically found in the all-anti conformation, which is not only the lowest-energy conformation, but it also makes for the largest surface area. If the long-chains were in the gauche conformation, they would be more clumped up and have a lower surface area. Having a large surface area means that the chains are more likely to attract each other by London dispersion forces, which also stabilizes the structure of the membrane.
This has implications how long-chained alkyl groups interact with one another, and influences the molecules’ physical properties, such as melting point. Many biologically-significant lipid molecules contain long-chain alkane groups. For example phospholipids form the structural basis of biological membranes. These lipids are a major component of the cell membrane that is the permeable barrier that surrounds the cell. The long-chain fatty acids that make up the membrane are typically found in the all-anti conformation, which is not only the lowest-energy conformation, but it also makes for the largest surface area. If the long-chains were in the gauche conformation, they would be more clumped up and have a lower surface area. Having a large surface area means that the chains are more likely to attract each other by London dispersion forces, which also stabilizes the structure of the membrane.
Questions to Answer
- Construct an explanation for why the potential energy of ethane changes as you rotate around the C-C bond. What is the interaction that is raising the potential energy? Where does the energy come from—so that the rotation around the C-C bond can occur?
- Construct a potential energy v dihedral angle diagram for propane, as you look down the C1-C2 bond. Label the maxima and minima with the corresponding Newman projections.
- Draw a schematic picture of a lipid bilayer made up of phospholipids (no need to draw every bond and atom). What would be the effect if the C-C bonds in phospholipids took up the less stable gauche conformation?
As we will see, cyclic compounds show some of the same kinds of energy changes with rotations around C-C bonds; conformations change from eclipsed to staggered. However, when the molecule is cyclic two other factors come into play and they complicate things a little. The first is that, by their very nature, ring compounds are more constrained; it is not possible to do a full 360º rotation around the C-C bonds without breaking a covalent bond (which requires more energy than is available through thermal collisions). There is, however, a range of rotations that most ring compounds can move through. The other factor involves rings that would have bond angles that are inconsistent with the ~109° bond angle that is usually found for sp3 hybridized carbons.
For example, consider the C-3 to C-6 cycloalkanes (→). We can calculate the bond angles for these regular polyhedrons if they were flat, that is, two-dimensional: they would range from 60° for cyclopropane to 120° for cyclohexane, both far outside 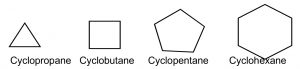 the range of sp3 bond angles. Not surprisingly, cycloalkanes behave in a range of different ways to minimize the strain imposed by both bond angles and the constraints on bond rotation. This ring strain can be experimentally determined by measuring the heats of combustion for cycloalkanes: the energy released by this reaction is a proxy for the stability of the particular cycloalkane. To compare among cycloalkanes, we need to calculate the heat of combustion per CH2 group, and as we will see shortly, six-membered rings do not, in fact, have any ring strain so we can determine the stabilities of differently sized rings compared to cyclohexane.
the range of sp3 bond angles. Not surprisingly, cycloalkanes behave in a range of different ways to minimize the strain imposed by both bond angles and the constraints on bond rotation. This ring strain can be experimentally determined by measuring the heats of combustion for cycloalkanes: the energy released by this reaction is a proxy for the stability of the particular cycloalkane. To compare among cycloalkanes, we need to calculate the heat of combustion per CH2 group, and as we will see shortly, six-membered rings do not, in fact, have any ring strain so we can determine the stabilities of differently sized rings compared to cyclohexane.
|
Cycloalkane |
Heat of combustion(kJ/mol) |
Heat of combustion per CH2 (kJ/mol) |
Ring Strain Compared to C6H12 (kJ/mol) |
Total Ring Strain = Ring strain x # of CH2 (kJ/mol) |
|
C3H6 |
-499.8 |
-166.3 |
9.2 |
27.6 |
|
C4H8 |
-655.9 |
-164 |
6.6 |
26.4 |
|
C5H10 |
-793.5 |
-158.7 |
1.3 |
6.5 |
|
C6H12 |
-944.5 |
-157.4 |
0 |
0 |
Heats of Combustion for the Cycloalkanes
Cyclopropane is actually the worst-case scenario: it has the highest strain because it is forced to exist as a flat, 2-D ring (since three points define a plane). If we look at a Newman projection of cyclohexane we can see that all the C–H and C–C bonds are eclipsed, which raises the potential energy of the molecule.
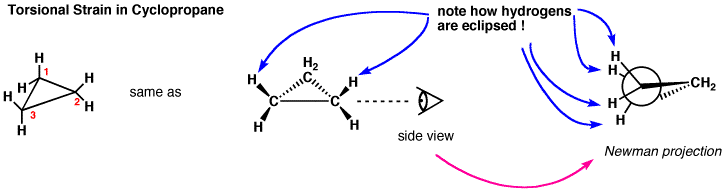 In an attempt to relieve some of the strain imposed by having a 60° bond angle, cyclopropane has bent bonds (sometimes called banana bonds).
In an attempt to relieve some of the strain imposed by having a 60° bond angle, cyclopropane has bent bonds (sometimes called banana bonds). 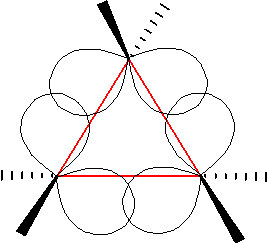 The electron density bulges out rather than being located between the two carbons, thus making the bond angle a little larger—however, there is still considerable strain. The combination of angle and eclipsing strain (also called torsional strain) explains why cyclopropane is a much more reactive species than its straight-chain analog, propane. There are a few naturally occurring three-membered ring compounds, but in general they are quite chemically reactive since the ring structure is quite unstable.
The electron density bulges out rather than being located between the two carbons, thus making the bond angle a little larger—however, there is still considerable strain. The combination of angle and eclipsing strain (also called torsional strain) explains why cyclopropane is a much more reactive species than its straight-chain analog, propane. There are a few naturally occurring three-membered ring compounds, but in general they are quite chemically reactive since the ring structure is quite unstable. 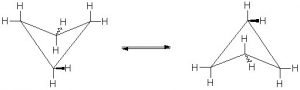 Four-membered rings are more stable—they have less angle strain because the ring is bigger and because the larger ring can bend a little, which has the effect of relieving some of the torsional strain.
Four-membered rings are more stable—they have less angle strain because the ring is bigger and because the larger ring can bend a little, which has the effect of relieving some of the torsional strain. 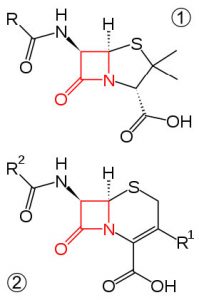 At room temperature, the cyclobutane ring is constantly bending so that each carbon can be relieved of a little of the strain. There are a number of important four-membered ring compounds that you may have run across: the antibiotics penicillin (1) and cephalosporin (2) have a four-membered amide ring as part of their structure (à). Normally (as we will see), amide groups are relatively stable (chemically nonreactive), but because this amide in the ring structure is constrained in a high-energy, four-membered ring, it is much more reactive than normal. Antibiotics act by targeting some part of the biochemistry of bacteria that will not affect the host organism (us). These antibiotics interfere with the synthesis and replication of the microbial cell wall, which is a type structure that most animals do not have (we have cell membranes).
At room temperature, the cyclobutane ring is constantly bending so that each carbon can be relieved of a little of the strain. There are a number of important four-membered ring compounds that you may have run across: the antibiotics penicillin (1) and cephalosporin (2) have a four-membered amide ring as part of their structure (à). Normally (as we will see), amide groups are relatively stable (chemically nonreactive), but because this amide in the ring structure is constrained in a high-energy, four-membered ring, it is much more reactive than normal. Antibiotics act by targeting some part of the biochemistry of bacteria that will not affect the host organism (us). These antibiotics interfere with the synthesis and replication of the microbial cell wall, which is a type structure that most animals do not have (we have cell membranes).
Ring stability improves with cyclopentane. If the molecule were flat, it would have almost exactly the sp3 bond angles between the ring carbons; this would mean, however, that all the bonds would be in the eclipsed conformation and the resulting torsional energy would be high. To relieve torsional strain the molecule bends into a sequence of “envelope” type shapes—again in dynamic and rapid motion so that the energy associated with the eclipsed conformation is reduced.
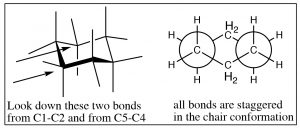 This brings us to cyclohexane, the “goldilocks” of cycloalkanes. The bending of the cyclohexane molecule can completely relieve all angle strain and torsional strain. In fact, cyclohexane is as stable as hexane—there is no ring strain associated with a six-membered ring.
This brings us to cyclohexane, the “goldilocks” of cycloalkanes. The bending of the cyclohexane molecule can completely relieve all angle strain and torsional strain. In fact, cyclohexane is as stable as hexane—there is no ring strain associated with a six-membered ring. 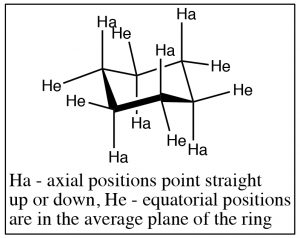 The most stable conformation of cyclohexane is known as the chair conformation, because one might imagine it as a chair with a footrest, seat, and back. In the chair conformation all the bonds are staggered, and all bond angles are 109º.
The most stable conformation of cyclohexane is known as the chair conformation, because one might imagine it as a chair with a footrest, seat, and back. In the chair conformation all the bonds are staggered, and all bond angles are 109º.
The groups attached to the cyclohexane ring can assume two types of positions: the positions that seem to point straight up or down are called axial, and the ones that are more in the plane of the ring are called equatorial. On each carbon, there is one axial and one equatorial position as shown (↑).
 Chair conformations can “ring-flip” as shown below. Here the structure on the left has all the axial positions in blue and the equatorial in red. Just as with the other rings, the ring is in constant motion and the bonds are rotating (as far as they can within the confines of the ring) so that the ring will “flip” back and forth between chair conformations, by bringing the chair back down and the footrest up. When this happens, axial substituents are converted to equatorial and vice versa. It’s worth noting that axial components can be “above” or “below” the ring plane; and the equatorial positions are also above or below the plane—but on average they lie in the plane of the ring. The other thing to notice is that while groups can flip between axial and equatorial, they do not flip from above to below. That is an axial substituent above the plane becomes and equatorial substituent above the plane.
Chair conformations can “ring-flip” as shown below. Here the structure on the left has all the axial positions in blue and the equatorial in red. Just as with the other rings, the ring is in constant motion and the bonds are rotating (as far as they can within the confines of the ring) so that the ring will “flip” back and forth between chair conformations, by bringing the chair back down and the footrest up. When this happens, axial substituents are converted to equatorial and vice versa. It’s worth noting that axial components can be “above” or “below” the ring plane; and the equatorial positions are also above or below the plane—but on average they lie in the plane of the ring. The other thing to notice is that while groups can flip between axial and equatorial, they do not flip from above to below. That is an axial substituent above the plane becomes and equatorial substituent above the plane.
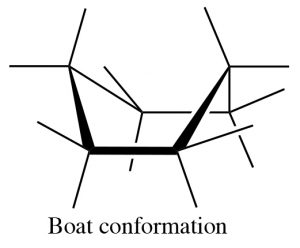 There are a number of conformations between one chair conformation and another, for example the boat conformation (→). This is a much more high-energy species since many of the bonds are eclipsed and there is a strong repulsion of the H’s at the 1 and 4 position.
There are a number of conformations between one chair conformation and another, for example the boat conformation (→). This is a much more high-energy species since many of the bonds are eclipsed and there is a strong repulsion of the H’s at the 1 and 4 position.
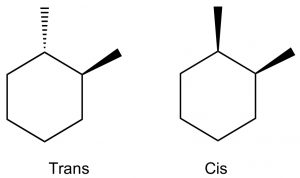
Mono-substituted cyclohexanes:
Now consider methylcyclohexane, the methyl group can be either axial or equatorial. When we look at Newman projections we see that the equatorial methyl group is in a more stable position, it is anti to the C-C bond in the ring, whereas an axial group is gauche to the ring C-C bond.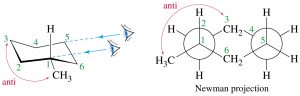
Equatorial methylcyclohexane
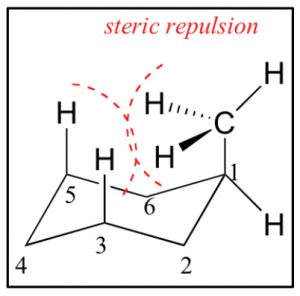
 In addition, an axial methyl group is also close to the axial hydrogens on carbons 3 and 5 in what is called a 1.3 diaxial interaction—which introduces another source of strain. Therefore, the more stable conformation is always equatorial.
In addition, an axial methyl group is also close to the axial hydrogens on carbons 3 and 5 in what is called a 1.3 diaxial interaction—which introduces another source of strain. Therefore, the more stable conformation is always equatorial.
Axial methylcyclohexane
For a methyl group the difference in energy is still quite small, and both axial and equatorial are present at room temperature, but as bulkier groups are introduced onto the ring, the preference for equatorial becomes even stronger. For example, cyclohexane rings with isopropyl (–CH(CH3)2) or t-butyl (-C(CH3)3) groups are locked into conformations where these groups are equatorial.
 Disubstituted cyclohexanes: When we get to cyclohexane rings that have two (or more) substituents, we need to consider whether the substituents are on the same (cis) or opposite (trans) sides of the ring. This is easiest to see if we first draw the ring flat and use a wedge dash representation to show relative positions of the groups. In these representations we don’t know whether the methyl groups oriented in axial or equatorial configurations (but we can figure it out), but what we do know is that these are different compounds, they cannot be interconverted by ring-flips like axial and equatorial—which are conformations of the same compound. To interconvert we would have to break the C-C bonds in the ring. These two compounds are called geometric isomers—they have the same molecular formula and connectivity but their atoms have a different (permanent) relationship in space (a different geometry).
Disubstituted cyclohexanes: When we get to cyclohexane rings that have two (or more) substituents, we need to consider whether the substituents are on the same (cis) or opposite (trans) sides of the ring. This is easiest to see if we first draw the ring flat and use a wedge dash representation to show relative positions of the groups. In these representations we don’t know whether the methyl groups oriented in axial or equatorial configurations (but we can figure it out), but what we do know is that these are different compounds, they cannot be interconverted by ring-flips like axial and equatorial—which are conformations of the same compound. To interconvert we would have to break the C-C bonds in the ring. These two compounds are called geometric isomers—they have the same molecular formula and connectivity but their atoms have a different (permanent) relationship in space (a different geometry).
We can determine the actual conformations that each isomer can take up by drawing the chair representation, and we can ring-flip to find the most stable conformation. 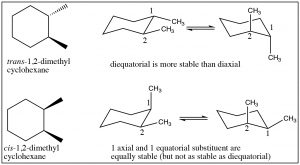 Remember that equatorial is always favored, so when we do this we can see that the trans isomer has a conformation in which both methyl groups are equatorial; whereas the cis conformation has both conformations where one is axial and one is equatorial. Therefore, we can conclude that the trans isomer is more stable than the cis. Note that the groups do not change their cis or trans relationship when the ring-flips.
Remember that equatorial is always favored, so when we do this we can see that the trans isomer has a conformation in which both methyl groups are equatorial; whereas the cis conformation has both conformations where one is axial and one is equatorial. Therefore, we can conclude that the trans isomer is more stable than the cis. Note that the groups do not change their cis or trans relationship when the ring-flips.
It is possible to do this kind of analysis for 1,3- and 1,4-disubstituted cyclohexanes, and even for more complex substances. For example, most sugars actually exist as ring structures in which the many alcohol groups (which are bigger than hydrogen) take up the equatorial position. For example, glucose exists as cyclic six-membered rings (one of the atoms is an oxygen but the principle is the same).
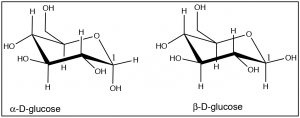 Note how almost all of the OH groups take up the equatorial position, except for the OH group on C-1 in α-D-glucose. These two forms of glucose are actually separate compounds. It is not possible to convert α-D-glucose to β-D-Glucose simply by a ring-flip (convince yourself that this is true by making model). We will see much more of these cyclic sugar molecules later in the course.
Note how almost all of the OH groups take up the equatorial position, except for the OH group on C-1 in α-D-glucose. These two forms of glucose are actually separate compounds. It is not possible to convert α-D-glucose to β-D-Glucose simply by a ring-flip (convince yourself that this is true by making model). We will see much more of these cyclic sugar molecules later in the course.
Questions to Answer
- Use excel to plot total ring strain vs ring size (number of CH2 units) as shown in Table 1. In addition use these total ring strain values for C7H14 (6.3 kJ/mol), and C8H16 (9.6 kJ/mol), C9H18 (12.6 kJ/mol). What trends do you see? How do you account for them?
- Draw two chair forms of cyclohexanol, which one is most stable? Is this a geometric isomer or a conformational isomer.
- Draw chair forms of cis and trans-1,3-dimethylcyclohexane and predict which geometric isomer is the most stable. Do the same for cis and trans-1,4-dimethylcyclohexane.
- Does 1,5-dimethylcyclohexane exist?
Optical Isomerism
 In the previous section we looked at conformational and geometric stereoisomerism, by which we mean that molecules that have the same molecular formula and connectivity of the atoms, but that have different arrangements in space. Conformational isomers can be interconverted by rotations around C-C bonds while geometric (cis/trans) isomers have permanently distinct geometries. Now we introduce another type of stereoisomer, known as optical isomers. Optical isomers have a property called chirality—they are mirror images of one another. While they have exactly the same overall shape, they are not superimposable on one another. One obvious example of macroscopic objects that are chiral are your hands.
In the previous section we looked at conformational and geometric stereoisomerism, by which we mean that molecules that have the same molecular formula and connectivity of the atoms, but that have different arrangements in space. Conformational isomers can be interconverted by rotations around C-C bonds while geometric (cis/trans) isomers have permanently distinct geometries. Now we introduce another type of stereoisomer, known as optical isomers. Optical isomers have a property called chirality—they are mirror images of one another. While they have exactly the same overall shape, they are not superimposable on one another. One obvious example of macroscopic objects that are chiral are your hands. 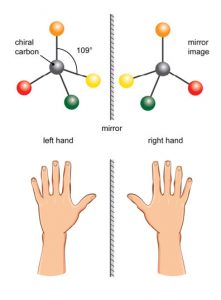 Your hands are mirror images of each other, but they are not superimposable on one another placing one hand on top of the other shows you that they are different as does the fact that a left hand glove does not fit your right hand. There are many objects in the world that are chiral. At the molecular level, many molecules are chiral—and it is often said that they exist in left- and right-handed forms.
Your hands are mirror images of each other, but they are not superimposable on one another placing one hand on top of the other shows you that they are different as does the fact that a left hand glove does not fit your right hand. There are many objects in the world that are chiral. At the molecular level, many molecules are chiral—and it is often said that they exist in left- and right-handed forms.
The simplest examples of chiral molecules are those that have a single carbon atom with four different substituents attached. While these compounds have exactly the same structure, connectivity and relationship between the atoms in space, they are different in the same way that a right and left hand are different: they are known as enantiomers—non-superimposable mirror images of each other. An equal mixture of enantiomers is called a racemate (racemic). Under normal laboratory conditions it is difficult to differentiate between a pair of enantiomers. If you were able to separate the left- from the right-handed forms, you would find that they have the same structure, the same physical and chemical properties, that is, the same melting point, boiling point, solubility, and chemical reactivity. Nevertheless, they are not identical—they can be distinguished by the way they interact with certain types of light.
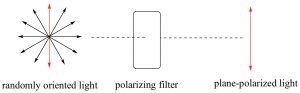 Electromagnetic radiation can be considered as being composed of electrical and magnetic (e-m) waves that oscillate perpendicular to each other and to the direction of wave transmission.
Electromagnetic radiation can be considered as being composed of electrical and magnetic (e-m) waves that oscillate perpendicular to each other and to the direction of wave transmission. 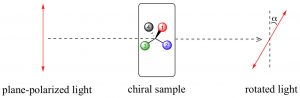 But a beam of light is not a single e-m wave; it consists of many such waves. The orientation of the various e-m waves within the beam are independent on one another and oriented randomly with respect to the direction of the beam. We can simplify an e-m wave by passing the light beam through what is known as a polarizer. A polarizer is a transparent material (it allows light to pass through it) composed of oriented crystalline that block all e-m oscillations that do not align with the crystal structure. The result is that the light that passes through the polarizer oscillates in only one plane; known as plane-polarized light. You can now make a prediction; if you place a second polarizing filter in the same orientation as the first, in the path of a plane-polarized light beam, the beam will pass through, but if you rotate the second filter by 90º to the first, the beam will be absorbed (blocked). This is an experiment you can do if you have polarizing sunglasses, which reduce glare by allowing light vibrating in only one direction to pass through. If the plane-polarized light interacts with an asymmetric electric field (such as the one generated by a chiral molecule), the plane of vibration will be rotated. We can measure the angle of rotation using another polarizing lens and in this way, we can detect the presence of chiral molecules. On the other hand, passing plane-polarized light through a racemic mixture (with 50% of each enantiomers present), or through a solution containing a non-chiral solute, will not affect the direction of the polarization plane.
But a beam of light is not a single e-m wave; it consists of many such waves. The orientation of the various e-m waves within the beam are independent on one another and oriented randomly with respect to the direction of the beam. We can simplify an e-m wave by passing the light beam through what is known as a polarizer. A polarizer is a transparent material (it allows light to pass through it) composed of oriented crystalline that block all e-m oscillations that do not align with the crystal structure. The result is that the light that passes through the polarizer oscillates in only one plane; known as plane-polarized light. You can now make a prediction; if you place a second polarizing filter in the same orientation as the first, in the path of a plane-polarized light beam, the beam will pass through, but if you rotate the second filter by 90º to the first, the beam will be absorbed (blocked). This is an experiment you can do if you have polarizing sunglasses, which reduce glare by allowing light vibrating in only one direction to pass through. If the plane-polarized light interacts with an asymmetric electric field (such as the one generated by a chiral molecule), the plane of vibration will be rotated. We can measure the angle of rotation using another polarizing lens and in this way, we can detect the presence of chiral molecules. On the other hand, passing plane-polarized light through a racemic mixture (with 50% of each enantiomers present), or through a solution containing a non-chiral solute, will not affect the direction of the polarization plane.
In a sample that rotates the plane of a plane-polarized light beam to the right, the enantiomer is designated as the (+ or dextrorotatory) isomer; if it rotates the plane-polarized light beam to the left it is referred to as the (– or levorotatory) isomer. This phenomenon is direct evidence of the existence of chiral molecules. The amount of rotation is dependent on the concentration of the substance in the solution, the path length of the sample tube, the wavelength of the incident light, and also the nature of the substance itself. We often report these rotations as a specific rotation, where all of these variables are defined, so that compounds can be identified by this property. Because of this phenomenon, substances that are chiral are said to be optically active.
Configurations of Chiral Molecules: the Cahn-Ingold-Prelog Convention
Since we cannot distinguish between enantiomers using the naming conventions that we have considered so far, we have to invoke a new convention to unambiguously specify the arrangement of bonds around a chiral center which is known as the configuration (not to be confused with conformation). The most common naming strategy used is referred to as the Cahn-Ingold-Prelog Convention: a set of rules that assigns a configuration (known as R or S) to a specific chiral (or stereogenic) center. An important fact to remember is that the configuration assigned to a molecule in this way has nothing to do with the molecule’s observed optical rotation.
Cahn-Ingold-Prelog Convention
- Look at each atom directly connected to a chiral carbon and rank by atomic number (Z); highest first (e.g. O>N>C). For isotopes the higher atomic mass receives a higher priority (e.g. D>H).
- If you can’t make a decision here, go out to the next atom in each chain—and so on until you get to the first point of difference. So for example, –CH2CH2OH takes priority over –CH2CH2CH2OH .
- Multiple bonds are equivalent to the same number of single-bonded atoms. For example, CH2=CH2 takes priority over –CH2CH3 because it is counted as if it were CH2(CH3)2 .
- Now place your eye so that you are looking down the bond from carbon to the lowest ranking group.
- If the sequence, high[latex]\rightarrow[/latex]low, is clockwise: R (Rectus).
- If the sequence, high[latex]\rightarrow[/latex]low, is counterclockwise: S (Sinister).
The skill of assigning configurations is one that takes practice and it is necessary to understand what the rules mean. Some common errors that people make are:
(a) Looking at the substituent as a whole rather than looking only at the atom (or the first atom that is different). 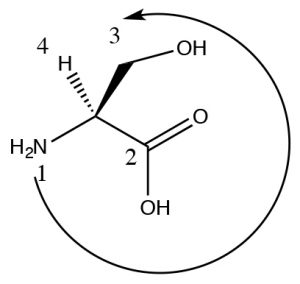 So for example, O > N > C, but also –OH > –CO2H even though CO2H is overall larger, it is attached by a C which is a lower priority than an O. Consider the example of this stereoisomer of the amino acid serine (It’s the L isomer but we will get to that in a while). The highest ranking group is the N (since its atomic number is higher than C), next is the CO2H because there are an equivalent of three C-O bonds on that carbon and only one C–O bond on the CH2OH group. Since the H is pointing back, we can now directly see that 1[latex]\rightarrow[/latex]2[latex]\rightarrow[/latex]3 is counterclockwise and the configuration is S.
So for example, O > N > C, but also –OH > –CO2H even though CO2H is overall larger, it is attached by a C which is a lower priority than an O. Consider the example of this stereoisomer of the amino acid serine (It’s the L isomer but we will get to that in a while). The highest ranking group is the N (since its atomic number is higher than C), next is the CO2H because there are an equivalent of three C-O bonds on that carbon and only one C–O bond on the CH2OH group. Since the H is pointing back, we can now directly see that 1[latex]\rightarrow[/latex]2[latex]\rightarrow[/latex]3 is counterclockwise and the configuration is S.
(b) Forgetting to look down the bond from the C to the lowest ranking group (often, but not always, an H). If you look down any other bond (or from the low ranking atom to the carbon) then you will almost certainly get the wrong assignment.
If the molecule is not drawn with the lowest ranking group pointing away, there are a number of options:
(1) Particularly when you are first getting started, you should MAKE A MODEL. There is research evidence that shows using an actual, physical model is the best way to learn this particular skill. Be careful to construct the model so that it looks exactly like the drawing. Then you can physically rotate it and identify the configuration.
or
(2) You can switch two groups—either redrawing or in your imagination (we strongly suggest you redraw it), so that the lowest group is now pointing back out of the plane. Then the configuration you get will be the opposite of the actual configuration.
or
(3) You could imagine yourself moving in space to look down the bond from C to the lowest ranking group. This is quite difficult for some people.
or
(4) You could rotate the molecule in your head so that you are looking down the bond from C to the lowest ranking group. This is also quite difficult for some people.
You should always use at least two methods – and make sure you get the same answer both
times!
After a while, this skill will come more easily to you.
R and S and D and L isomers:
 As you probably already know, most biological molecules are chiral. For example, all of the naturally-occurring amino acids (aside from glycine) have a chiral carbon (see above), sugars have several chiral centers, and so the large molecules made up from these smaller monomers (such as nucleic acids, carbohydrates, lipids, polypeptides, and a range of smaller molecules) contain one or more (sometimes many) chiral carbons. For historical reasons, however, most simple biological molecules (that is the monomers from which polymers are constructed) are referred to as either D or L isomers, rather than R or S. The convention for naming substances as D or L dates back to the early 1900s and has to do with a compound’s similarity to glyceraldehyde which exists as a pair of enantiomers. The enantiomer that rotated light to the right (+) was identified as D, and the other one (–) as L. For example, the naturally-occurring amino acids are the L-isomer, and many of the simple sugars are the D isomer. It should be noted that a compound such as glucose can be identified as D-glucose, even though it contains 5 chiral centers. The D/L nomenclature is applied to the molecule as a whole, whereas the R/S nomenclature applies to a specific chiral carbon. The D/L nomenclature does not, in fact, predict the direction of rotation of polarized light in most larger molecules—but it is a much simpler way of naming compounds with more than one chiral center.
As you probably already know, most biological molecules are chiral. For example, all of the naturally-occurring amino acids (aside from glycine) have a chiral carbon (see above), sugars have several chiral centers, and so the large molecules made up from these smaller monomers (such as nucleic acids, carbohydrates, lipids, polypeptides, and a range of smaller molecules) contain one or more (sometimes many) chiral carbons. For historical reasons, however, most simple biological molecules (that is the monomers from which polymers are constructed) are referred to as either D or L isomers, rather than R or S. The convention for naming substances as D or L dates back to the early 1900s and has to do with a compound’s similarity to glyceraldehyde which exists as a pair of enantiomers. The enantiomer that rotated light to the right (+) was identified as D, and the other one (–) as L. For example, the naturally-occurring amino acids are the L-isomer, and many of the simple sugars are the D isomer. It should be noted that a compound such as glucose can be identified as D-glucose, even though it contains 5 chiral centers. The D/L nomenclature is applied to the molecule as a whole, whereas the R/S nomenclature applies to a specific chiral carbon. The D/L nomenclature does not, in fact, predict the direction of rotation of polarized light in most larger molecules—but it is a much simpler way of naming compounds with more than one chiral center.
Speaking of which…
Molecules with two or more chiral (stereogenic) centers
Molecules that have more than one chiral center bring in another level of complexity. It can be quite difficult to draw molecules accurately that have more than one chiral center, and therefore we often turn to a representation that is more stylized than the wedge-dash; this is known as the Fischer projection, named after Emil Fischer (1852-1919) who elucidated the structures of sugars (and who also introduced the D/L nomenclature). Fischer projections are written as vertical and horizontal lines. The carbon backbone is the vertical line, and the other substituents are horizontal. We assume that the horizontal bonds are coming out towards you (↓). This convention makes it easier to draw and to assign configuration to the chiral centers (this structure is S). 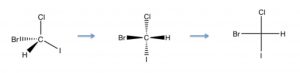 Now if we look at Fischer projections for a four carbon sugar that has two chiral centers, we see that there can be several possibilities.
Now if we look at Fischer projections for a four carbon sugar that has two chiral centers, we see that there can be several possibilities.
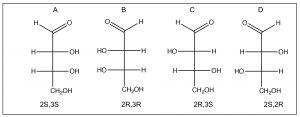
Numbering from the aldehyde carbon as carbon 1, both C2 and C3 are chiral. We also see that there are two pairs of enantiomers: A and B are mirror images of each other and so are C and D. In general, for a molecule with n chiral centers, there are a possibility of 2n stereoisomers. When we look at the relationship between isomer A and isomer C (or D) we note that they are not mirror images of each other (the chiral centers are the same at one carbon and different at the other). These compounds are known as diastereomers, that is, stereoisomers that are not mirror images of one another; they do not have identical distances between all of their atoms. Because they have different arrangements in space, diastereomers have different properties, both physical and chemical, and can be separated. In fact, the two compounds have different names: A and B are called erythrose while C and D are called threose. Diastereomers actually belong to the same class of stereoisomers as cis/trans ring compounds (and alkenes), they have the same molecular formula and connectivity, but have different arrangements in space and cannot be interconverted by bond rotations. In contrast, enantiomers have the same atomic arrangements in space, but cannot be superimposed on one another.
So now you might well ask yourself, given that stereoisomers have the same physical properties: how could you possibility separate enantiomers? 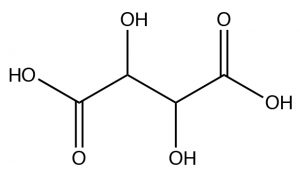 The existence of enantiomers was first observed by Louis Pasteur (1882-1895), who was actually able to identify different crystalline forms of tartaric acid[3] (actually, the potassium salt), which turned out to be the two enantiomers (but not the meso isomer), which appeared as tiny crystals that were mirror images of each other. In fact, this selective recrystallization is highly unusual, and it is normally not possible to selectively recrystallize isomers.
The existence of enantiomers was first observed by Louis Pasteur (1882-1895), who was actually able to identify different crystalline forms of tartaric acid[3] (actually, the potassium salt), which turned out to be the two enantiomers (but not the meso isomer), which appeared as tiny crystals that were mirror images of each other. In fact, this selective recrystallization is highly unusual, and it is normally not possible to selectively recrystallize isomers.
So why does the stereo-asymmetry of a molecule matter? The answer is that organisms (living systems) are—apparently due to an accident of their origin and subsequent evolution—asymmetric at the molecular level. For example, polypeptides and proteins are polymers of amino acids. While organisms can make and use both D- and L-form amino acids, all of the amino acids used in polypeptide/protein synthesis (with the exception of glycine, which is achiral) exist in L- and D- forms. Only L-form amino acids are used in polypeptides and proteins. The use of only L-form amino acids means that each polypeptide/protein has a distinct three-dimensional shape that influence how other molecules bind to it. For example, a particular drug can be designed to inhibit a particular enzyme (protein-based catalyst).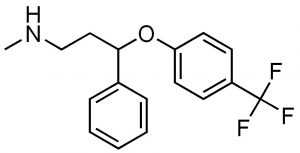 If the drug is itself chiral, then it is extremely likely that one or the other of its chiral forms will be an effective inhibitor while the others will not. In fact, it is common for drug companies to first patent the racemic mixture of a drug, and then later the purified enantiomers. For example, Fluoxetine (Prozac)(→) is a racemic mixture of the two enantiomers (can you find the chiral center?). In the human body, the two forms of fluoxetine are metabolized into corresponding forms of norfluoxetine, one of which is significantly more active than the other.[4] Another example of the use of a racemic drug is the terrible story of thalidomide, which was marketed in the 1960’s in Europe and Canada as a drug for morning sickness.
If the drug is itself chiral, then it is extremely likely that one or the other of its chiral forms will be an effective inhibitor while the others will not. In fact, it is common for drug companies to first patent the racemic mixture of a drug, and then later the purified enantiomers. For example, Fluoxetine (Prozac)(→) is a racemic mixture of the two enantiomers (can you find the chiral center?). In the human body, the two forms of fluoxetine are metabolized into corresponding forms of norfluoxetine, one of which is significantly more active than the other.[4] Another example of the use of a racemic drug is the terrible story of thalidomide, which was marketed in the 1960’s in Europe and Canada as a drug for morning sickness. 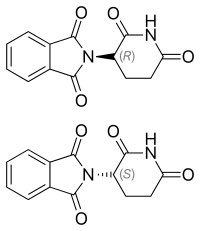 The original drug was administered as the racemic mixture but we know that it is the R isomer that is the sedative. The S isomer is teratogenic. That is, it causes birth defects in this case associated with the development of limbs. Many children were born without limbs before Thalidomide was removed from the market. Now we know that even the pure R enantiomer racemizes at physiological pH. In fact, Thalidomide was re-introduced to the market because it is one of the few drugs that can be used to treat leprosy.
The original drug was administered as the racemic mixture but we know that it is the R isomer that is the sedative. The S isomer is teratogenic. That is, it causes birth defects in this case associated with the development of limbs. Many children were born without limbs before Thalidomide was removed from the market. Now we know that even the pure R enantiomer racemizes at physiological pH. In fact, Thalidomide was re-introduced to the market because it is one of the few drugs that can be used to treat leprosy.
Non-chiral species with chiral centers.
Just because a compound has a chiral (stereogenic) center, doesn’t mean the actual compound is optically active. Remember that the requirement for a chiral substance is that there is no symmetry element. Consider the set of compounds below.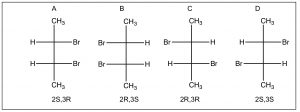
There appear to be four stereoisomers here, but, in fact, there are only three. Isomers A and B are identical due to the a mirror plane through the center of the molecule (bisecting the C2-3 bond), the top half of the molecule is identical to the bottom half. Compounds like this are called meso isomers. The meso isomer is a diastereomer of the pair of enantiomers C and D.
Questions to Answer
- Without looking at the diagram above, construct your own representation and explanation for the various types of isomers that we have encountered. Give an example of each type of isomerism (using two such isomers) and explain how and why they differ from each other and from other types of isomers.
- How is it possible that compounds with chiral carbons are not themselves chiral?
- Do you think it is possible to have a chiral compound that does not have chiral carbons in it? What structural features would you look for? Why?
Questions to Ponder
- Most biomolecules are chiral, how do you think they got that way?
- Most biomolecules are chiral, what are the implications for the synthesis of pharmacologically active compounds?
- Recall that this is not the case for sp2 or sp hybridized carbon, which also form pi bonds, where the orbital overlap is destroyed by rotation. Therefore, as we will see later, a much higher input of energy is required for compounds with pi bonds to rotate the bonding carbons relative to each other. ↵
- See Chapter 1 and Chapter 4 in CLUE text. ↵
- https://en.wikipedia.org/wiki/Tartaric_acid ↵
- Wikipedia on fluoxetine: https://en.wikipedia.org/wiki/Fluoxetine ↵

