"

Work, Energy, and Energy Resources

48 Power

Learning Objectives

  • Calculate power by determining the rate of energy transfer or work done over time, using biological or mechanical systems as examples (e.g., human muscle work, cellular energy use, or lifting objects).

  • Analyze power consumption in practical scenarios, including household appliances, laboratory equipment, and clinical devices.

  • Calculate the cost of energy consumption, using the relationship between power, time, and energy, and applying real-world units like kilowatt-hours (kWh) and electricity rates.

What is Power and Its Biological and Mechanical Significance

In biosciences and health-related disciplines, the concept of power is essential for understanding how energy is used and transferred in biological systems. Whether you’re analyzing the metabolic output of muscles, the energy consumption of a medical imaging device, or the rate at which a person performs physical activity, power is the rate at which energy is used or work is done.

Power is defined as:

 [latex]P = \frac{W}{t}[/latex]

where:

  • [latex]P[/latex] is power, measured in watts (W),

  • [latex]W[/latex] is work or energy transferred, in joules (J),

  • [latex]t[/latex] is the time in seconds (s) over which the energy transfer occurs.

One watt is equivalent to one joule per second:

 [latex]1~\text{W} = 1~\text{J/s}[/latex]

Understanding Power in Everyday Contexts

Power gives us a way to measure how quickly energy is being used or produced. A 60-watt light bulb, for instance, converts 60 joules of electrical energy into light and heat every second. In physiology, when we talk about how quickly a muscle contracts or how much energy a person expends during physical activity, we are dealing with power.

Figure 48.1 demonstrates this concept with a vivid example.

 

A space shuttle rocket is being launched and is burning propellant.
Figure 48.1: This powerful rocket on the Space Shuttle Endeavor did work and consumed energy at a very high rate. (credit: NASA)

In biomechanics, if a person lifts a 20-kg weight to shoulder height in 2 seconds, they are exerting power. The faster the lift, the more power required. This makes power a critical concept in strength training, rehabilitation, and even cardiovascular testing where energy expenditure over time is key.

Power in Biological Systems

In living organisms, the body uses chemical energy stored in molecules like ATP to perform work—muscle contractions, neuron firing, or cellular transport. Power can be applied to these situations by analyzing how fast energy is used.

For example, consider a 70-kg person climbing stairs at a steady pace. If the person ascends a 3-meter-high staircase in 6 seconds, we can calculate the power required to perform this vertical work.

  1. Calculate the work done (which is equivalent to the change in gravitational potential energy):

[latex]W = mgh = (70~\text{kg})(9.81~\text{m/s}^2)(3~\text{m}) = 2050~\text{J}[/latex]

  1. Then, use the definition of power:

 [latex]P = \frac{2050~\text{J}}{6~\text{s}} \approx 342~\text{W}[/latex]

This person is generating about 342 watts of power during the climb—similar to the power used by a few incandescent light bulbs!

Calculating Power from Energy

Example 48.1: Calculating the Power to Climb Stairs

What is the power output for a 60.0-kg woman who runs up a 3.00 m high flight of stairs in 3.50 s, starting from rest but having a final speed of 2.00 m/s? (See Figure 48.2.)

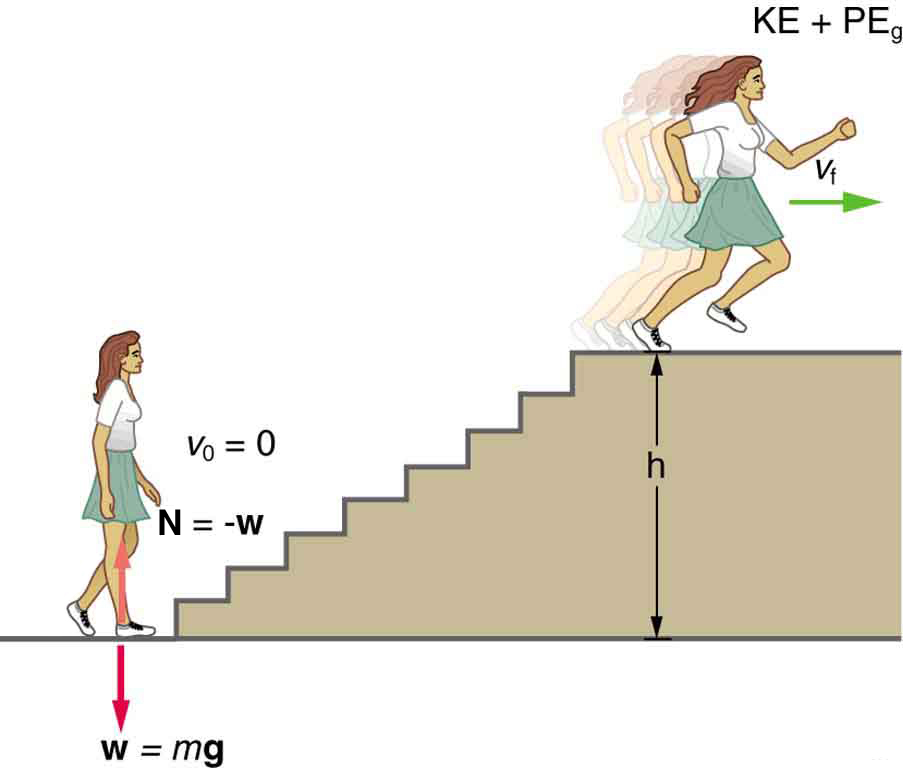
A woman is standing before a set of stairs with her weight shown by a vector w pointing vertically downward, which is equal to m times g. The normal force N acting on the woman is shown by a vector pointing vertically upward, which is equal to negative w. Her velocity at this point is v sub 0 equal to zero. She runs and reaches the top of the stairs at a height h with velocity v sub f. Now she possesses potential energy as well as kinetic energy labeled as K E plus P E sub g.
Figure 48.2: When this woman runs upstairs starting from rest, she converts the chemical energy originally from food into kinetic energy and gravitational potential energy. Her power output depends on how fast she does this.

Strategy and Concept

The work going into mechanical energy is [latex]W\text{= KE + PE}[/latex]. At the bottom of the stairs, we take both [latex]\text{KE}[/latex] and
[latex]{\text{PE}}_{g}[/latex] as initially zero; thus,
[latex]W={\text{KE}}_{f}+{\text{PE}}_{g}=\frac{1}{2}{{\mathrm{mv}}_{f}}^{2}+\text{mgh}[/latex], where [latex]h[/latex] is the vertical height of the stairs. Because all terms are given, we can calculate [latex]W[/latex] and then divide it by time to get power.

Solution

Substituting the expression for [latex]W[/latex] into the definition of power given in the previous equation, [latex]P=W/t[/latex] yields

[latex]P=\frac{W}{t}=\frac{\frac{1}{2}{{\text{mv}}_{f}}^{2}+\text{mgh}}{t}\text{.}[/latex]

Entering known values yields

[latex]P = \frac{0.5(\text{60.0 kg}){(\text{2.00 m/s})}^{2}+(\text{60.0 kg})({\text{9.80 m/s}}^{2})(\text{3.00 m})}{\text{3.50 s}} = \frac{\text{120 J}+\text{1764 J}}{\text{3.50 s}}=\text{538 W.}[/latex]

Discussion

The woman does 1764 J of work to move up the stairs compared with only 120 J to increase her kinetic energy; thus, most of her power output is required for climbing rather than accelerating.

It is impressive that this woman’s useful power output is slightly less than 1 horsepower [latex](\text{1 hp}=\text{746 W})[/latex]! People can generate more than a horsepower with their leg muscles for short periods of time by rapidly converting available blood sugar and oxygen into work output. (A horse can put out 1 hp for hours on end.) Once oxygen is depleted, power output decreases and the person begins to breathe rapidly to obtain oxygen to metabolize more food—this is known as the aerobic stage of exercise. If the woman climbed the stairs slowly, then her power output would be much less, although the amount of work done would be the same.

Making Connections: Take-Home Investigation—Measure Your Power Rating

Try this simple activity to estimate your own power output:

  1. Measure the vertical height of a flight of stairs ([latex]h[/latex]).

  2. Record your mass in kilograms ([latex]m[/latex]).

  3. Time how long it takes to walk or run to the top ([latex]t[/latex]).

Assume most energy goes into increasing potential energy (ignore kinetic energy):

[latex]P = \frac{mgh}{t}[/latex]

Where:

  • [latex]P[/latex] = power (in watts)

  • [latex]m[/latex] = your mass (kg)

  • [latex]g = 9.81~\text{m/s}^2[/latex] (acceleration due to gravity)

  • [latex]h[/latex] = height climbed (m)

  • [latex]t[/latex] = time (s)

Typical results will be around [latex]300 - 500~\text{W}[/latex], or approximately [latex]0.5~\text{hp}[/latex] (horsepower).

Determine your own power rating by measuring the time it takes you to climb a flight of stairs. We will ignore the gain in kinetic energy, as the above example showed that it was a small portion of the energy gain. Don’t expect that your output will be more than about 0.5 hp.

Examples of Power

Power appears in nearly all biological and physical processes—from muscle contractions and metabolism to machinery and weather events. Power always involves a rate of energy transfer or conversion. Table 48.1 shows a wide range of power levels across systems in nature, biology, and technology.

Solar Radiation and Earth

The Sun delivers power to Earth’s surface at roughly:

[latex]1.3~\text{kW/m}^2[/latex]

Only a small fraction is stored long-term. Most energy becomes thermal energy or is radiated back into space. This mismatch between power supply and storage helps explain why fossil fuels are nonrenewable.

Inefficiency in Energy Conversion

Conversion between forms of energy is never perfect. For example:

  • A 60-W light bulb emits only 5 W as visible light.

  • The rest (55 W) becomes thermal energy.

Even in large systems:

  • A coal-fired power plant may generate 1000 MW of electrical power.

  • It consumes about 2500 MW of chemical energy.

  • So, 1500 MW is lost as waste heat, usually dispersed using cooling towers (see Figure 48.3).

A distant view of a coal-fired power plant with clearly visible cooling towers generating electric power and emitting a large amount of gases.
Figure 48.3: Tremendous amounts of electric power are generated by coal-fired power plants such as this one in China, but an even larger amount of power is lost to heat transfer. The cooling towers dissipate thermal energy into the atmosphere. This thermal loss is unavoidable in most fuel-based power generation systems.
(credit: Kleinolive, Wikimedia Commons)
Table 48.1: Power Output or Consumption
Object or Phenomenon Power in Watts
Supernova (at peak) [latex]5×{\text{10}}^{\text{37}}[/latex]
Milky Way galaxy [latex]{\text{10}}^{\text{37}}[/latex]
Crab Nebula pulsar [latex]{\text{10}}^{\text{28}}[/latex]
The Sun [latex]4×{\text{10}}^{\text{26}}[/latex]
Volcanic eruption (maximum) [latex]4×{\text{10}}^{\text{15}}[/latex]
Lightning bolt [latex]2×{\text{10}}^{\text{12}}[/latex]
Nuclear power plant (total electric and heat transfer) [latex]3×{\text{10}}^{9}[/latex]
Aircraft carrier (total useful and heat transfer) [latex]{\text{10}}^{8}[/latex]
Dragster (total useful and heat transfer) [latex]2×{\text{10}}^{6}[/latex]
Car (total useful and heat transfer) [latex]8×{\text{10}}^{4}[/latex]
Football player (total useful and heat transfer) [latex]5×{\text{10}}^{3}[/latex]
Clothes dryer [latex]4×{\text{10}}^{3}[/latex]
Person at rest (all heat transfer) [latex]\text{100}[/latex]
Typical incandescent light bulb (total useful and heat transfer) [latex]\text{60}[/latex]
Heart, person at rest (total useful and heat transfer) [latex]8[/latex]
Electric clock [latex]3[/latex]
Pocket calculator [latex]{\text{10}}^{-3}[/latex]

Power and Energy Consumption

Understanding energy use is vital in medical, research, and household settings. Power tells us how fast energy is being used, and energy tells us how much is used.

We can calculate the energy used with:

[latex]E = Pt[/latex]

Where:

  • [latex]E[/latex] is energy (in joules)

  • [latex]P[/latex] is power (in watts)

  • [latex]t[/latex] is time (in seconds)

In practice, electricity is billed in kilowatt-hours ([latex]\text{kW} \cdot \text{h}[/latex]):

[latex]1~\text{kW} \cdot \text{h} = 1000~\text{W} \times 3600~\text{s} = 3.6 \times 10^6~\text{J}[/latex]

So, a 1000-W (1 kW) heater running for 2 hours uses:

[latex]E = (1~\text{kW}) \cdot (2~\text{h}) = 2~\text{kW} \cdot \text{h}[/latex]

If electricity costs $0.12 per kWh, the total cost is:

[latex]\text{Cost} = 2 \times 0.12 = $0.24[/latex]

Example 48.2: Calculating Energy Costs

What is the cost of running a 0.200-kW computer 6.00 h per day for 30.0 d if the cost of electricity is $0.120 per [latex]\text{kW}\cdot h[/latex]?

Strategy

Cost is based on energy consumed; thus, we must find [latex]E[/latex] from [latex]E=\text{Pt}[/latex] and then calculate the cost. Because electrical energy is expressed in [latex]\text{kW}\cdot h[/latex], at the start of a problem such as this it is convenient to convert the units into [latex]\text{kW}[/latex] and hours.

Solution

The energy consumed in [latex]\text{kW}\cdot \text{h}[/latex] is

[latex]\begin{array}{lll}E& =& \text{Pt}=(0\text{.}\text{200}\phantom{\rule{0.20em}{0ex}}\text{kW})(6\text{.}\text{00}\phantom{\rule{0.20em}{0ex}}\text{h/d})(\text{30}\text{.}0\phantom{\rule{0.20em}{0ex}}\text{d})\\ & =& \text{}\text{36}\text{.}\text{0 kW}\cdot \text{h,}\end{array}[/latex]

and the cost is simply given by

[latex]\text{cost}=(\text{36.0 kW}\cdot h)(\$0.120 per kW\cdot h)=\$4.32 \text{ per month.}[/latex]

Discussion

The cost of using the computer in this example is neither exorbitant nor negligible. It is clear that the cost is a combination of power and time. When both are high, such as for an air conditioner in the summer, the cost is high.

Energy Awareness and Practical Cost-Saving

As energy prices rise, the motivation to reduce consumption becomes not only environmental but also economic. From a physics perspective, energy used over time can be expressed as:

[latex]E = P \cdot t[/latex]

Where:

  • [latex]E[/latex] is energy in joules (or kilowatt-hours),

  • [latex]P[/latex] is power in watts (or kilowatts),

  • [latex]t[/latex] is time in seconds (or hours).

This equation helps us estimate the cost of using electrical devices. To reduce energy usage and save money, either the power consumption or time of operation must decrease.

Focus on High-Impact Devices

From a cost-saving perspective, focus on devices that:

  • Use high power,

  • Run for long durations.

These include:

  • Water heaters

  • HVAC systems (heating and air conditioning)

  • Refrigerators

In contrast:

  • A toaster uses high power but for short periods.

  • An electric clock runs constantly, but consumes very little power (e.g., 3 W).

Efficiency Matters

Replacing devices with more efficient alternatives is one of the easiest ways to save energy. For example:

  • A compact fluorescent lightbulb (CFL) uses about 15 W to produce the same light as a 60 W incandescent bulb.

  • This means:
    [latex]\text{Efficiency ratio} = \frac{60~\text{W}}{15~\text{W}} = 4[/latex]
    The CFL is four times more efficient in converting electrical energy to light.

Sustainability and Energy Transformation

While energy is conserved in an isolated system, its usefulness for doing work decreases with each transformation. This phenomenon is central to thermodynamics, discussed in detail in later chapters.

Every energy transformation leads to some portion of energy becoming thermal energy, often as waste heat. This energy spreads into the environment and is difficult to harness again for useful work. This degradation of energy is not a loss in quantity, but a loss in quality—its ability to perform useful biological or mechanical work diminishes.

Global Perspective

Modern society consumes vast amounts of energy—much of it from fossil fuels. These fuels:

  • Release large quantities of carbon dioxide ([latex]\text{CO}_2[/latex]),

  • Contribute to global warming and climate change,

  • Are non-renewable and finite.

To address these challenges, it is crucial to:

  • Reduce energy use wherever possible,

  • Transition to non-fossil and renewable energy sources,

  • Improve energy efficiency in every sector—transportation, medicine, home heating, industry, and research.

Real-World Relevance: Health Sciences and Energy

In biomedical and life sciences:

  • Understanding energy consumption in hospital equipment (e.g., MRI machines, incubators, ventilators) can inform cost-saving strategies.

  • Refrigeration and storage of medicines and biological samples depend on high-efficiency, continuous energy systems.

  • Energy audits in medical facilities can reduce waste while ensuring patient care standards are met.

Section Summary

  • Power is the rate at which work is done or energy is transferred. It quantifies how quickly energy is used or transformed in physical, biological, or technological systems.

  • The formula for average power [latex]P[/latex], when work [latex]W[/latex] is done over a time interval [latex]t[/latex], is:

    [latex]P = \frac{W}{t}[/latex]

  • The SI unit of power is the watt (W), defined as:

    [latex]1~\text{W} = 1~\text{J/s}[/latex]

  • In some contexts, such as medical equipment or mechanical systems, power is also expressed in horsepower (hp). The conversion is:

    [latex]1~\text{hp} = 746~\text{W}[/latex]

Conceptual Questions

  1. Most electrical appliances are rated in watts. Does this rating depend on how long the appliance is on? (When off, it is a zero-watt device.) Explain in terms of the definition of power.
  2. Explain, in terms of the definition of power, why energy consumption is sometimes listed in kilowatt-hours rather than joules. What is the relationship between these two energy units?
  3. A spark of static electricity, such as that you might receive from a doorknob on a cold dry day, may carry a few hundred watts of power. Explain why you are not injured by such a spark.

Problems & Exercises

  1. The Crab Nebula (see Figure 48.4) pulsar is the remnant of a supernova that occurred in A.D. 1054. Using data from Table 48.1, calculate the approximate factor by which the power output of this astronomical object has declined since its explosion.
    A supernova explosion.
    Figure 48.4: Crab Nebula (credit: ESO, via Wikimedia Commons)
  2. Suppose a star 1000 times brighter than our Sun (that is, emitting 1000 times the power) suddenly goes supernova. Using data from Table 48.1: (a) By what factor does its power output increase? (b) How many times brighter than our entire Milky Way galaxy is the supernova? (c) Based on your answers, discuss whether it should be possible to observe supernovas in distant galaxies. Note that there are on the order of [latex]{\text{10}}^{\text{11}}[/latex] observable galaxies, the average brightness of which is somewhat less than our own galaxy.
  3. A person in good physical condition can put out 100 W of useful power for several hours at a stretch, perhaps by pedaling a mechanism that drives an electric generator. Neglecting any problems of generator efficiency and practical considerations such as resting time: (a) How many people would it take to run a 4.00-kW electric clothes dryer? (b) How many people would it take to replace a large electric power plant that generates 800 MW?
  4. What is the cost of operating a 3.00-W electric clock for a year if the cost of electricity is ?0.0900 per [latex]\text{kW}\cdot h[/latex]?
  5. A large household air conditioner may consume 15.0 kW of power. What is the cost of operating this air conditioner 3.00 h per day for 30.0 d if the cost of electricity is ?0.110 per [latex]\text{kW}\cdot h[/latex]?
  6. (a) What is the average power consumption in watts of an appliance that uses [latex]5\text{.}\text{00 kW}\cdot h[/latex] of energy per day? (b) How many joules of energy does this appliance consume in a year?
  7. (a) What is the average useful power output of a person who does [latex]6\text{.}\text{00}×{\text{10}}^{6}\phantom{\rule{0.20em}{0ex}}\text{J}[/latex] of useful work in 8.00 h? (b) Working at this rate, how long will it take this person to lift 2000 kg of bricks 1.50 m to a platform? (Work done to lift his body can be omitted because it is not considered useful output here.)
  8. A 500-kg dragster accelerates from rest to a final speed of 110 m/s in 400 m (about a quarter of a mile) and encounters an average frictional force of 1200 N. What is its average power output in watts and horsepower if this takes 7.30 s?
  9. (a) How long will it take an 850-kg car with a useful power output of 40.0 hp (1 hp = 746 W) to reach a speed of 15.0 m/s, neglecting friction? (b) How long will this acceleration take if the car also climbs a 3.00-m-high hill in the process?
  10. (a) Find the useful power output of an elevator motor that lifts a 2500-kg load a height of 35.0 m in 12.0 s, if it also increases the speed from rest to 4.00 m/s. Note that the total mass of the counterbalanced system is 10,000 kg—so that only 2500 kg is raised in height, but the full 10,000 kg is accelerated. (b) What does it cost, if electricity is ?0.0900 per [latex]\text{kW}\cdot h[/latex]?
  11. (a) What is the available energy content, in joules, of a battery that operates a 2.00-W electric clock for 18 months? (b) How long can a battery that can supply [latex]8\text{.}\text{00}×{\text{10}}^{4}\phantom{\rule{0.20em}{0ex}}\text{J}[/latex] run a pocket calculator that consumes energy at the rate of [latex]1\text{.}\text{00}×{\text{10}}^{-3}\phantom{\rule{0.20em}{0ex}}\text{W}[/latex]?
  12. (a) How long would it take a [latex]1\text{.}\text{50}×{\text{10}}^{5}[/latex]-kg airplane with engines that produce 100 MW of power to reach a speed of 250 m/s and an altitude of 12.0 km if air resistance were negligible? (b) If it actually takes 900 s, what is the power? (c) Given this power, what is the average force of air resistance if the airplane takes 1200 s? (Hint: You must find the distance the plane travels in 1200 s assuming constant acceleration.)
  13. Calculate the power output needed for a 950-kg car to climb a [latex]2.00º[/latex] slope at a constant 30.0 m/s while encountering wind resistance and friction totaling 600 N. Explicitly show how you follow the steps in the Problem-Solving Strategies for Energy.
  14. (a) Calculate the power per square meter reaching Earth’s upper atmosphere from the Sun. (Take the power output of the Sun to be [latex]4\text{.}\text{00}×{\text{10}}^{\text{26}}\phantom{\rule{0.25em}{0ex}}\text{W}\text{.})[/latex] (b) Part of this is absorbed and reflected by the atmosphere, so that a maximum of [latex]1\text{.}{\text{30 kW/m}}^{2}[/latex] reaches Earth’s surface. Calculate the area in [latex]{\text{km}}^{2}[/latex] of solar energy collectors needed to replace an electric power plant that generates 750 MW if the collectors convert an average of 2.00% of the maximum power into electricity. (This small conversion efficiency is due to the devices themselves, and the fact that the sun is directly overhead only briefly.) With the same assumptions, what area would be needed to meet the United States’ energy needs [latex](1\text{.}\text{05}×{\text{10}}^{\text{20}}\phantom{\rule{0.25em}{0ex}}\text{J})?[/latex] Australia’s energy needs [latex](5\text{.}4×{\text{10}}^{\text{18}}\phantom{\rule{0.25em}{0ex}}\text{J)?}[/latex] China’s energy needs [latex](6\text{.}3×{\text{10}}^{\text{19}}\phantom{\rule{0.25em}{0ex}}\text{J)?}[/latex] (These energy consumption values are from 2006.)

Glossary

power
the rate at which work is done
watt
(W) SI unit of power, with [latex]\text{1 W}=\text{1 J/s}[/latex]
horsepower
an older non-SI unit of power, with [latex]\text{1 hp}=\text{746 W}[/latex]
kilowatt-hour
[latex](\text{kW}\cdot h)[/latex] unit used primarily for electrical energy provided by electric utility companies
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book