Work, Energy, and Energy Resources
47 Conservation of Energy
Learning Objectives
-
Explain the law of conservation of energy in biological and physical systems.
-
Describe major forms of energy relevant to life processes and health technologies.
-
Define and calculate efficiency in energy transformations, such as metabolism and devices.
-
Apply conservation principles to human motion, metabolism, and medical technologies
Law of Conservation of Energy
In bioscience and health contexts, energy is everywhere: from cellular respiration to muscle contraction and body temperature regulation. The law of conservation of energy states:
Total energy is constant in any process. It may change in form or move between systems, but it is never created or destroyed.
This principle is essential for understanding metabolic processes, physical activity, and medical technologies.
Energy in the Human Body and Environment
We’ve already discussed mechanical energy, which includes:
-
Kinetic Energy (KE): energy of motion (e.g., a running patient),
-
Potential Energy (PE): stored energy due to position (e.g., lifting a leg during rehab).
Energy can also be transferred through nonconservative work (e.g., friction, heat):
[latex]{W}_{\text{nc}}[/latex]
To account for all other forms of energy (like chemical, thermal, or electrical), we define:
[latex]\text{OE} = \text{Other Energy}[/latex]
So the general form of the energy conservation equation is:
[latex]{\text{KE}}_{i} + {\text{PE}}_{i} + W_{\text{nc}} + {\text{OE}}_{i} = {\text{KE}}_{f} + {\text{PE}}_{f} + {\text{OE}}_{f}[/latex]
In clinical scenarios, [latex]\text{OE}[/latex] often includes:
-
Chemical energy from food or medication
-
Electrical energy in nerves or ECG devices
-
Thermal energy from metabolism or inflammation
Forms of Energy in Life Sciences
Some biologically relevant forms of energy include:
-
Chemical Energy: Stored in food (e.g., glucose, fats); released in metabolism.
-
Thermal Energy: Maintains body temperature; increases during fever or exercise.
-
Electrical Energy: Used in neural signaling and medical imaging (e.g., EEG, ECG).
-
Radiant Energy: Light used in vision, vitamin D synthesis, and phototherapy.
-
Nuclear Energy: Relevant in medical imaging and cancer treatment.
These forms interconvert according to conservation principles.
In Figure 47.1 solar energy is converted to electrical energy by solar panels, then to mechanical energy via motors. Similar principles apply in solar-powered prosthetics or biosensors.
Table 47.1 gives the amount of energy stored, used, or released from various objects and in various phenomena. The range of energies and the variety of types and situations is impressive.
Problem-Solving Strategies for Energy
-
Define the system (e.g., patient, cell, joint).
-
Identify forms of energy and forces involved.
-
Use mechanical energy conservation when all forces are conservative:
[latex]{\text{KE}}_{i} + {\text{PE}}_{i} = {\text{KE}}_{f} + {\text{PE}}_{f}[/latex]
-
When nonconservative forces or chemical processes are involved, use:
[latex]{\text{KE}}_{i} + {\text{PE}}_{i} + W_{\text{nc}} + {\text{OE}}_{i} = {\text{KE}}_{f} + {\text{PE}}_{f} + {\text{OE}}_{f}[/latex]
-
Simplify by eliminating zeros (e.g., [latex]{\text{PE}}_{\text{i}} = 0[/latex] at reference height).
-
Solve and check physical and physiological plausibility.
Energy Transformation in the Real World
Example: Eating a banana
-
Chemical energy (glucose) → ATP
-
ATP → Kinetic energy in muscle contraction + thermal energy for heat regulation
Example: A defibrillator
-
Electrical energy from capacitor → electrical energy in heart muscle → kinetic energy of contraction
Example: Solar-powered medical drone
-
Solar energy → electrical energy → mechanical energy for flight (see Figure 47.1)
Efficiency of Energy Transformations
In real systems, not all input energy becomes useful output. For example, during exercise, much energy is lost as heat.
Efficiency is given by:
[latex]\text{Efficiency} = \frac{W_{\text{out}}}{E_{\text{in}}}[/latex]
or as a percentage:
[latex]\text{Efficiency} = \left( \frac{W_{\text{out}}}{E_{\text{in}}} \right) \times 100%[/latex]
Table 47.2 lists some efficiencies of mechanical devices and human activities. In a coal-fired power plant, for example, about 40% of the chemical energy in the coal becomes useful electrical energy. The other 60% transforms into other (perhaps less useful) energy forms, such as thermal energy, which is then released to the environment through combustion gases and cooling towers.
| Activity/device | Efficiency (%)1 |
|---|---|
| Cycling and climbing | 20 |
| Swimming, surface | 2 |
| Swimming, submerged | 4 |
| Shoveling | 3 |
| Weightlifting | 9 |
| Steam engine | 17 |
| Gasoline engine | 30 |
| Diesel engine | 35 |
| Nuclear power plant | 35 |
| Coal power plant | 42 |
| Electric motor | 98 |
| Compact fluorescent light | 20 |
| Gas heater (residential) | 90 |
| Solar cell | 10 |
PhET Explorations: Masses and Springs
This interactive simulation models a realistic spring-mass system, allowing students to explore how energy is stored and transferred in mechanical systems—concepts that are foundational for biomechanics, rehabilitation, and physiology.
In this simulation, you can:
-
Hang various masses from springs and watch them oscillate.
-
Adjust the stiffness of the spring ([latex]k[/latex]) and the damping (energy loss).
-
View how energy is converted among:
-
Kinetic Energy (KE) — due to motion of the mass,
-
Elastic Potential Energy (PE) — stored in the stretched or compressed spring,
-
Thermal Energy — lost due to damping (simulating friction or internal resistance).
-
-
Slow down time to see the oscillations in more detail.
-
Change planetary settings to test the effect of different gravitational accelerations (e.g., simulating bone-loading on the Moon or Mars).
This tool can help you understand:
-
How energy conservation applies in oscillating systems.
-
How spring stiffness and mass influence biological structures (e.g., tendons, ligaments, and prosthetic materials).
-
The relevance of damping to rehabilitation equipment and joint biomechanics.
Section Summary
-
The law of conservation of energy states that the total energy in a closed system remains constant. Energy may change form (e.g., from chemical to thermal or kinetic) or be transferred between systems, but it is never created or destroyed.
-
When all forms of energy are taken into account, the general energy conservation equation becomes:
[latex]{\text{KE}}_{i} + {\text{PE}}_{i} + W_{\text{nc}} + {\text{OE}}_{i} = {\text{KE}}_{f} + {\text{PE}}_{f} + {\text{OE}}_{f}[/latex]
where:
-
[latex]{\text{KE}}[/latex] is kinetic energy (e.g., motion of a limb),
-
[latex]{\text{PE}}[/latex] is potential energy (e.g., from height or spring tension),
-
[latex]{W}_{\text{nc}}[/latex] is work done by nonconservative forces (e.g., friction, air resistance),
-
[latex]{\text{OE}}[/latex] is other forms of energy, such as thermal, chemical, electrical, or nuclear energy.
-
-
Common forms of energy in biological and health contexts include:
-
Chemical energy (from food or ATP),
-
Thermal energy (body heat, metabolism),
-
Electrical energy (nerve signals, membrane potentials),
-
Radiant energy (light in vision or photosynthesis),
-
Nuclear energy (used in medical imaging and treatments).
-
-
Although energy is conserved, it cannot all be converted into useful work. Some energy is lost as heat or becomes unusable in the process (entropy increases).
-
The efficiency [latex]\text{Eff}[/latex] of an energy conversion process (such as muscle contraction, metabolism, or a mechanical device) is calculated as:
[latex]\text{Eff}=\frac{{W}{\text{out}}}{{E}{\text{in}}}[/latex]
where:
-
[latex]{W}_{\text{out}}[/latex] is the useful work output (e.g., lifting a weight),
-
[latex]{E}_{\text{in}}[/latex] is the total energy input (e.g., food calories consumed).
-
Conceptual Questions
- Consider the following scenario. A car for which friction is not negligible accelerates from rest down a hill, running out of gasoline after a short distance. The driver lets the car coast farther down the hill, then up and over a small crest. He then coasts down that hill into a gas station, where he brakes to a stop and fills the tank with gasoline. Identify the forms of energy the car has, and how they are changed and transferred in this series of events. (See Figure 47.3.)
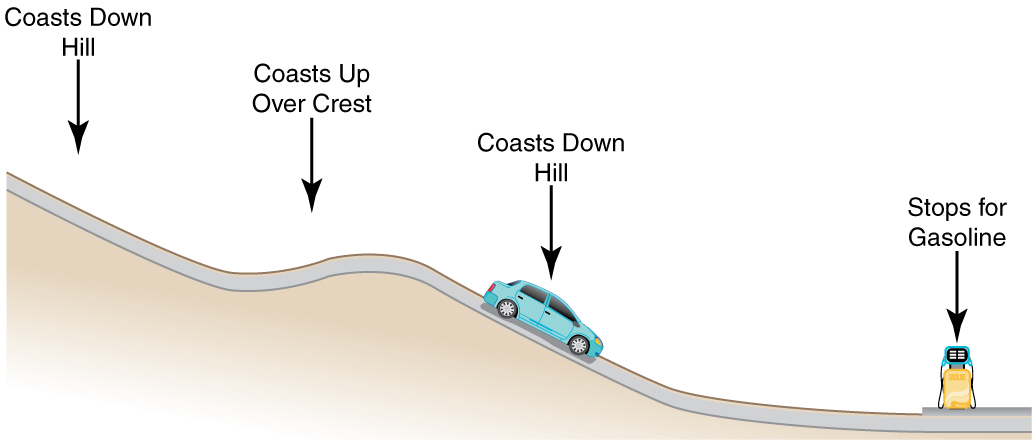
Figure 47.3: A car experiencing non-negligible friction coasts down a hill, over a small crest, then downhill again, and comes to a stop at a gas station. - Describe the energy transfers and transformations for a javelin, starting from the point at which an athlete picks up the javelin and ending when the javelin is stuck into the ground after being thrown.
- Do devices with efficiencies of less than one violate the law of conservation of energy? Explain.
- List four different forms or types of energy. Give one example of a conversion from each of these forms to another form.
- List the energy conversions that occur when riding a bicycle.
Problems & Exercises
- Using values from Table 47.1, how many DNA molecules could be broken by the energy carried by a single electron in the beam of an old-fashioned TV tube? (These electrons were not dangerous in themselves, but they did create dangerous x rays. Later model tube TVs had shielding that absorbed x rays before they escaped and exposed viewers.)
- Using energy considerations and assuming negligible air resistance, show that a rock thrown from a bridge 20.0 m above water with an initial speed of 15.0 m/s strikes the water with a speed of 24.8 m/s independent of the direction thrown.
- If the energy in fusion bombs were used to supply the energy needs of the world, how many of the 9-megaton variety would be needed for a year’s supply of energy (using data from Table 47.1)? This is not as far-fetched as it may sound—there are thousands of nuclear bombs, and their energy can be trapped in underground explosions and converted to electricity, as natural geothermal energy is.
- (a) Use of hydrogen fusion to supply energy is a dream that may be realized in the next century. Fusion would be a relatively clean and almost limitless supply of energy, as can be seen from Table 47.1. To illustrate this, calculate how many years the present energy needs of the world could be supplied by one millionth of the oceans’ hydrogen fusion energy. (b) How does this time compare with historically significant events, such as the duration of stable economic systems?
Footnotes
- 1 Representative values
Glossary
- law of conservation of energy
- the general law that total energy is constant in any process; energy may change in form or be transferred from one system to another, but the total remains the same
- electrical energy
- the energy carried by a flow of charge
- chemical energy
- the energy in a substance stored in the bonds between atoms and molecules that can be released in a chemical reaction
- radiant energy
- the energy carried by electromagnetic waves
- nuclear energy
- energy released by changes within atomic nuclei, such as the fusion of two light nuclei or the fission of a heavy nucleus
- thermal energy
- the energy within an object due to the random motion of its atoms and molecules that accounts for the object’s temperature
- efficiency
- a measure of the effectiveness of the input of energy to do work; useful energy or work divided by the total input of energy
the general law that total energy is constant in any process; energy may change in form or be transferred from one system to another, but the total remains the same
the energy carried by a flow of charge
the energy in a substance stored in the bonds between atoms and molecules that can be released in a chemical reaction
the energy carried by electromagnetic waves
energy released by changes within atomic nuclei, such as the fusion of two light nuclei or the fission of a heavy nucleus
the energy within an object due to the random motion of its atoms and molecules that accounts for the object's temperature
a measure of the effectiveness of the input of energy to do work; useful energy or work divided by the total input of energy
