"

Work, Energy, and Energy Resources

43 Kinetic Energy and the Work-Energy Theorem

Learning Objectives

  • Explain work as a transfer of energy.

  • Define and calculate net work.

  • Apply the work-energy theorem to systems with changing kinetic energy.

Work Transfers Energy

When a force does work on a system, energy is transferred into or out of the system. The form of that energy transfer depends on the situation:

  • If the system is moving at a constant speed against a resistive force (like friction), the energy added by the applied force is continuously dissipated—often as heat.

  • If a force moves an object vertically (like lifting a briefcase), energy is stored as gravitational potential energy, which can be recovered later.

Example: Lifting a stone to build a pyramid stores potential energy in the Earth-stone system. That energy remains until it is released by lowering the stone.

Net Work and the Work-Energy Theorem

Net work is the work done by the net external force on an object. When a net force accelerates an object, it gives it kinetic energy, which is the energy of motion.

For a constant force acting in the direction of displacement, the net work is:

[latex]W_{\text{net}} = F_{\text{net}} d \cos \theta[/latex]

  • [latex]F_{\text{net}}[/latex] is the net external force,

  • [latex]d[/latex] is the displacement,

  • [latex]\theta[/latex] is the angle between the force and displacement vectors.

Graphical Interpretation of Work

The area under a graph of [latex]F \cos \theta[/latex] versus [latex]d[/latex]  like in Figure 43.1 represents the total work done:

  • If the force is constant, the area is a rectangle:
    [latex]W = Fd \cos \theta[/latex].

  • If the force varies, break the graph into strips and sum the area of each segment.

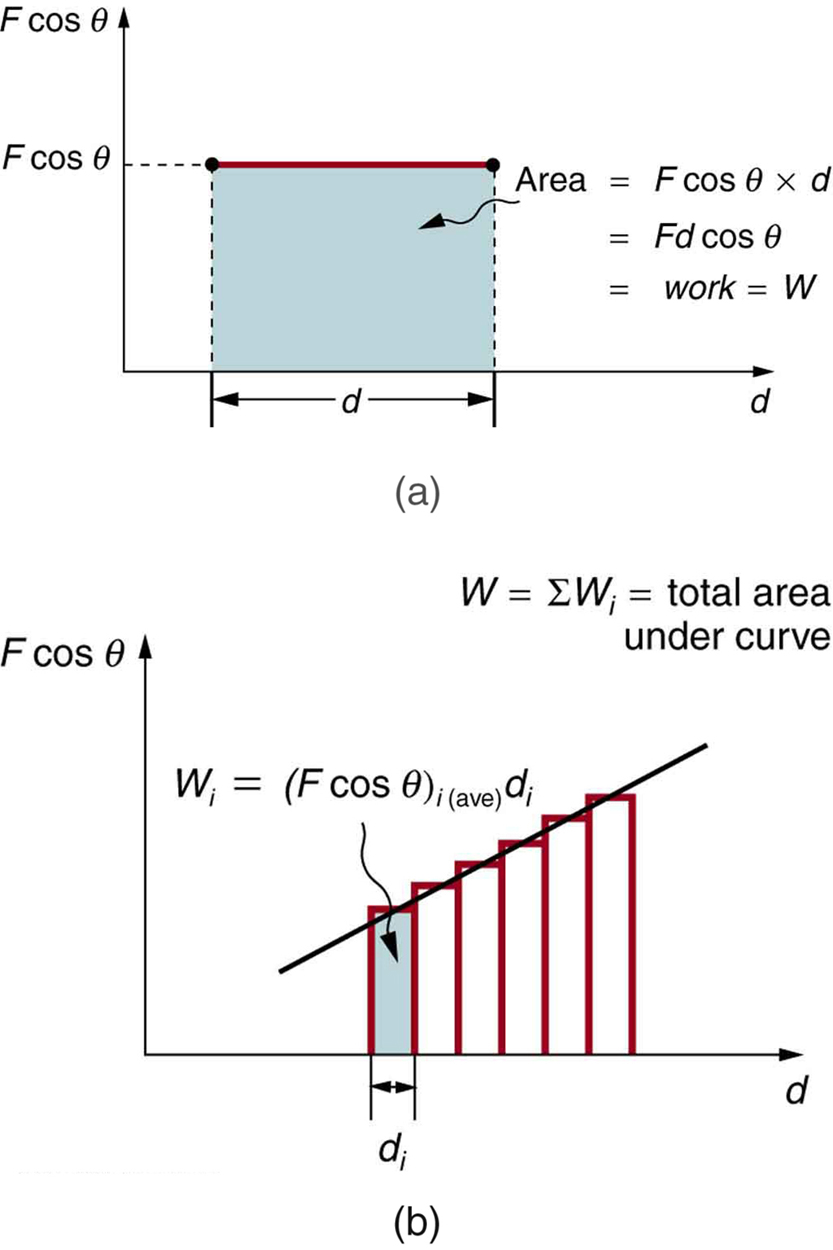
Two drawings labele a and b. (a) A graph of force component F cosine theta versus distance d. d is along the x axis and F cosine theta is along the y axis. A line of length d is drawn parallel to the horizontal axis for some value of F cosine theta. Area under this line in the graph is shaded and is equal to F cosine theta multiplied by d. F d cosine theta is equal to work W. (b) A graph of force component F cosine theta versus distance d. d is along the x axis and F cosine theta is along the y axis. There is an inclined line and the area under it is divided into many thin vertical strips of width d sub i. The area of one vertical stripe is equal to average value of F cosine theta times d sub i which equals to work W sub i.
Figure 43.1: (a) A graph of [latex]F \cos \theta[/latex] vs. [latex]d[/latex], when the force is constant. The area under the curve represents the work done.
(b) A graph where the force varies. The work done for each small segment is the area of the strip; the total area gives the total work.

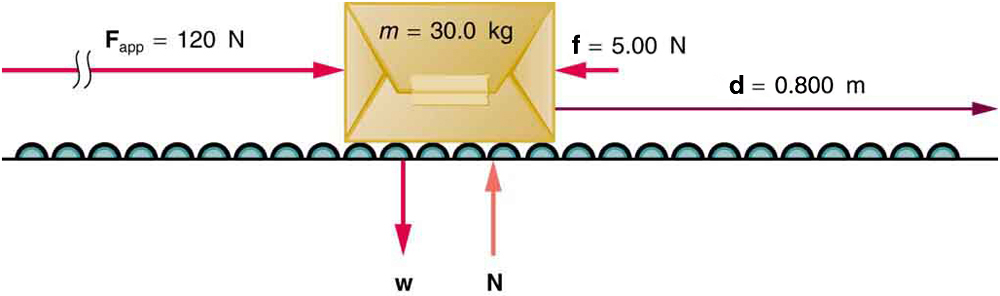
Net work will be simpler to examine if we consider a one-dimensional situation where a force is used to accelerate an object in a direction parallel to its initial velocity. Such a situation occurs for the package on the roller belt conveyor system shown in Figure 43.2.

A package shown on a roller belt pushed with a force F towards the right shown by a vector F sub app equal to one hundred and twenty newtons. A vector w is in the downward direction starting from the bottom of the package and the reaction force N on the package is shown by the vector N pointing upwards at the bottom of the package. A frictional force vector of five point zero zero newtons acts on the package leftwards. The displacement d is shown by the vector pointing to the right with a value of zero point eight zero zero meters.
Figure 43.2: A package on a roller belt is pushed horizontally through a distance [latex]\mathbf{d}[/latex].

The Work-Energy Theorem

Let’s derive a relationship between net work and kinetic energy using Newton’s second law and kinematic equations.

  1. Start with Newton’s second law:

    [latex]F_{\text{net}} = ma[/latex]

  2. Multiply both sides by displacement [latex]d[/latex]:

    [latex]W_{\text{net}} = mad[/latex]

  3. From kinematics, recall:

    [latex]v^2 = v_0^2 + 2ad[/latex] → [latex]a = \frac{v^2 - v_0^2}{2d}[/latex]

  4. Substituting into the equation for work:

    [latex]W_{\text{net}} = m \left( \frac{v^2 - v_0^2}{2d} \right) d = \frac{1}{2}mv^2 - \frac{1}{2}mv_0^2[/latex]

Work-Energy Theorem

The net work done on a system equals the change in kinetic energy of that system:

[latex]W_{\text{net}} = \frac{1}{2}mv^2 - \frac{1}{2}mv_0^2[/latex]

Kinetic Energy

We define kinetic energy (KE) as the energy of motion:

[latex]\text{KE} = \frac{1}{2}mv^2[/latex]

  • [latex]m[/latex] is the mass of the object (in kg),

  • [latex]v[/latex] is its speed (in m/s).

Kinetic energy increases quadratically with speed. For example, doubling a car’s speed quadruples its kinetic energy. This explains why high-speed collisions are so dangerous.

Example 43.1: Calculating the Kinetic Energy of a Package

Suppose a 30.0-kg package on the roller belt conveyor system in Figure 43.2 is moving at 0.500 m/s. What is its kinetic energy?

Strategy

Because the mass [latex]m[/latex] and speed [latex]v[/latex] are given, the kinetic energy can be calculated from its definition as given in the equation [latex]\text{KE}=\frac{1}{2}{\text{mv}}^{2}[/latex].

Solution

The kinetic energy is given by

[latex]\text{KE}=\frac{1}{2}{\text{mv}}^{2}\text{.}[/latex]

Entering known values gives

[latex]\text{KE}=0\text{.}5\left(\text{30.0 kg}\right)\left(\text{0.500 m/s}\right)^{2},[/latex]

which yields

[latex]\text{KE}=\text{3.75 kg}\cdot {m}^{2}{\text{/s}}^{2}=\text{3.75 J.}[/latex]

Discussion

Note that the unit of kinetic energy is the joule, the same as the unit of work, as mentioned when work was first defined. It is also interesting that, although this is a fairly massive package, its kinetic energy is not large at this relatively low speed. This fact is consistent with the observation that people can move packages like this without exhausting themselves.

Example 43.2: Determining the Work to Accelerate a Package

Suppose that you push on the 30.0-kg package in Figure 43.2 with a constant force of 120 N through a distance of 0.800 m, and that the opposing friction force averages 5.00 N.

(a) Calculate the net work done on the package. (b) Solve the same problem as in part (a), this time by finding the work done by each force that contributes to the net force.

Strategy and Concept for (a)

This is a motion in one dimension problem, because the downward force (from the weight of the package) and the normal force have equal magnitude and opposite direction, so that they cancel in calculating the net force, while the applied force, friction, and the displacement are all horizontal. (See Figure 43.2.) As expected, the net work is the net force times distance.

Solution for (a)

The net force is the push force minus friction, or [latex]{F}_{\text{net}}\text{= 120 N – 5}\text{.}\text{00 N = 115 N}[/latex]. Thus the net work is

[latex]\begin{array}{lll}{W}_{\text{net}}& =& {F}_{\text{net}}d=\left(\text{115 N}\right)\left(\text{0.800 m}\right)\\ & =& \text{92.0 N}\cdot m=\text{92.0 J.}\end{array}[/latex]

Discussion for (a)

This value is the net work done on the package. The person actually does more work than this, because friction opposes the motion. Friction does negative work and removes some of the energy the person expends and converts it to thermal energy. The net work equals the sum of the work done by each individual force.

Strategy and Concept for (b)

The forces acting on the package are gravity, the normal force, the force of friction, and the applied force. The normal force and force of gravity are each perpendicular to the displacement, and therefore do no work.

Solution for (b)

The applied force does work.

[latex]\begin{array}{lll}{W}_{\text{app}}& =& {F}_{\text{app}}d\phantom{\rule{0.25em}{0ex}}\text{cos}\left(0º\right)={F}_{\text{app}}d\\ & =& \left(\text{120 N}\right)\left(\text{0.800 m}\right)\\ & =& \text{96.0 J}\end{array}[/latex]

The friction force and displacement are in opposite directions, so that [latex]\theta =\text{180º}[/latex], and the work done by friction is

[latex]\begin{array}{lll}{W}_{\text{fr}}& =& {F}_{\text{fr}}d\phantom{\rule{0.25em}{0ex}}\text{cos}\left(\text{180º}\right)=-{F}_{\text{fr}}d\\ & =& -\left(\text{5.00 N}\right)\left(\text{0.800 m}\right)\\ & =& -\text{4.00 J.}\end{array}[/latex]

So the amounts of work done by gravity, by the normal force, by the applied force, and by friction are, respectively,

[latex]\begin{array}{lll}{W}_{\text{gr}}& =& 0,\\ {W}_{N}& =& 0,\\ {W}_{\text{app}}& =& \text{96.0 J,}\\ {W}_{\text{fr}}& =& -\text{4.00 J.}\end{array}[/latex]

The total work done as the sum of the work done by each force is then seen to be

[latex]{W}_{\text{total}}={W}_{\text{gr}}+{W}_{N}+{W}_{\text{app}}+{W}_{\text{fr}}=\text{92}\text{.0 J}.[/latex]

Discussion for (b)

The calculated total work [latex]{W}_{\text{total}}[/latex] as the sum of the work by each force agrees, as expected, with the work [latex]{W}_{\text{net}}[/latex] done by the net force. The work done by a collection of forces acting on an object can be calculated by either approach.

Example 43.3: Determining Speed from Work and Energy

Find the speed of the package in Figure 43.2 at the end of the push, using work and energy concepts.

Strategy

Here the work-energy theorem can be used, because we have just calculated the net work, [latex]{W}_{\text{net}}[/latex], and the initial kinetic energy,
[latex]\frac{1}{2}{m{v}_{0}}^{2}[/latex]. These calculations allow us to find the final kinetic energy, [latex]\frac{1}{2}{\text{mv}}^{2}[/latex], and thus the final speed [latex]v[/latex].

Solution

The work-energy theorem in equation form is

[latex]{W}_{\text{net}}=\frac{1}{2}{\text{mv}}^{2}-\frac{1}{2}{m{v}_{0}}^{2}\text{.}[/latex]

Solving for [latex]\frac{1}{2}{\text{mv}}^{2}[/latex] gives

[latex]\frac{1}{2}{\text{mv}}^{\text{2}}={W}_{\text{net}}+\frac{1}{2}{m{v}_{0}}^{2}\text{.}[/latex]

Thus,

[latex]\frac{1}{2}{\text{mv}}^{2}=\text{92}\text{.}0 J+3\text{.}\text{75 J}=\text{95.}\text{75 J.}[/latex]

Solving for the final speed as requested and entering known values gives

[latex]\begin{array}{lll}v& =& \sqrt{\frac{2\text{(95.75 J)}}{m}}=\sqrt{\frac{\text{191.5 kg}\cdot {m}^{2}{\text{/s}}^{2}}{\text{30.0 kg}}}\\ & =& \text{2.53 m/s.}\end{array}[/latex]

Discussion

Using work and energy, we not only arrive at an answer, we see that the final kinetic energy is the sum of the initial kinetic energy and the net work done on the package. This means that the work indeed adds to the energy of the package.

Example 43.3: Work and Energy Can Reveal Distance, Too

How far does the package in Figure 43.2 coast after the push, assuming friction remains constant? Use work and energy considerations.

Strategy

We know that once the person stops pushing, friction will bring the package to rest. In terms of energy, friction does negative work until it has removed all of the package’s kinetic energy. The work done by friction is the force of friction times the distance traveled times the cosine of the angle between the friction force and displacement; hence, this gives us a way of finding the distance traveled after the person stops pushing.

Solution

The normal force and force of gravity cancel in calculating the net force. The horizontal friction force is then the net force, and it acts opposite to the displacement, so [latex]\theta =\text{180º}[/latex]. To reduce the kinetic energy of the package to zero, the work [latex]{W}_{\text{fr}}[/latex] by friction must be minus the kinetic energy that the package started with plus what the package accumulated due to the pushing. Thus [latex]{W}_{\text{fr}}=-\text{95}\text{.}\text{75 J}[/latex]. Furthermore, [latex]{W}_{\text{fr}}=fd\prime \phantom{\rule{0.25em}{0ex}}\text{cos}\phantom{\rule{0.25em}{0ex}}\theta \phantom{\rule{0.25em}{0ex}}\text{= –}fd\prime[/latex], where [latex]d\prime[/latex] is the distance it takes to stop. Thus,

[latex]d\prime =-\frac{{W}_{\text{fr}}}{f}=-\frac{-\text{95.75 J}}{\text{5.00 N}},[/latex]

and so

[latex]d\prime =\text{19}\text{.2 m}.[/latex]

Discussion

This is a reasonable distance for a package to coast on a relatively friction-free conveyor system. Note that the work done by friction is negative (the force is in the opposite direction of motion), so it removes the kinetic energy.

Many problems in physics can be solved either by applying Newton’s laws or by using the principles of energy. While force-based approaches involving kinematics and dynamics can yield correct results, they often require more steps and less intuitive reasoning. In contrast, energy methods—especially using the work-energy theorem—tend to be more concise and conceptually transparent. They offer deeper insight into the system by highlighting how energy is transferred or transformed. Thus, energy-based approaches are not only powerful tools for problem-solving but also essential for building a broader understanding of physical processes.

Section Summary

  • Net work [latex]W_{\text{net}}[/latex] is the work done by the net external force acting on a system.

  • Work transfers energy: When work is done on an object, energy is added to or removed from the system.

  • The translational kinetic energy of an object of mass [latex]m[/latex] and speed [latex]v[/latex] is
    [latex]\text{KE} = \frac{1}{2}mv^2[/latex].

  • The work-energy theorem states that the net work done on a system is equal to the change in its kinetic energy:
    [latex]W_{\text{net}} = \frac{1}{2}mv^2 - \frac{1}{2}mv_0^2[/latex]

  • Solving problems using energy principles can be simpler and more insightful than using Newton’s laws and kinematics alone, especially for systems where forces and displacements are known but accelerations are difficult to measure.

Conceptual Questions

  1. The person in Figure 43.3 does work on the lawn mower. Under what conditions would the mower gain energy? Under what conditions would it lose energy?
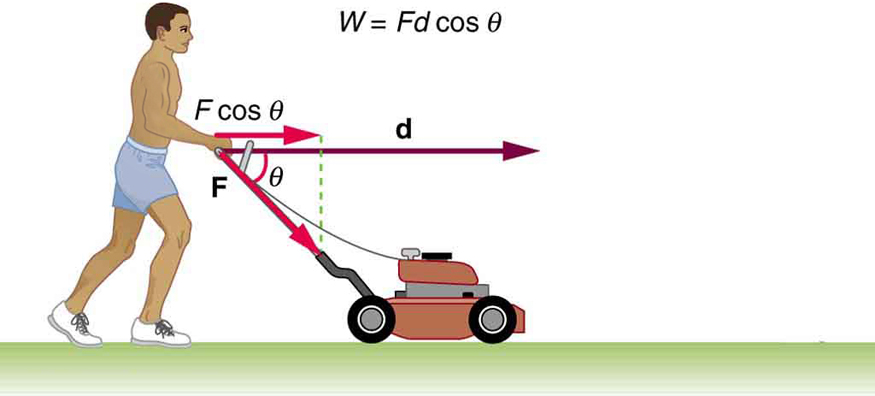
    A person pushing a lawn mower with a force F. Force is represented by a vector making an angle theta below the horizontal and distance moved by the mover is represented by vector d. The component of vector F along vector d is F cosine theta. Work done by the person, W, is equal to F d cosine theta.
    Figure 43.3
  2. Work done on a system puts energy into it. Work done by a system removes energy from it. Give an example for each statement.

Problems & Exercises

  1. Compare the kinetic energy of a 20,000-kg truck moving at 110 km/h with that of an 80.0-kg astronaut in orbit moving at 27,500 km/h.(a) How fast must a 3000-kg elephant move to have the same kinetic energy as a 65.0-kg sprinter running at 10.0 m/s? (b) Discuss how the larger energies needed for the movement of larger animals would relate to metabolic rates.
  2. Confirm the value given for the kinetic energy of an aircraft carrier in Table 47.1. You will need to look up the definition of a nautical mile (1 knot = 1 nautical mile/h).
  3. (a) Calculate the force needed to bring a 950-kg car to rest from a speed of 90.0 km/h in a distance of 120 m (a fairly typical distance for a non-panic stop). (b) Suppose instead the car hits a concrete abutment at full speed and is brought to a stop in 2.00 m. Calculate the force exerted on the car and compare it with the force found in part (a).
  4. A car’s bumper is designed to withstand a 4.0-km/h (1.1-m/s) collision with an immovable object without damage to the body of the car. The bumper cushions the shock by absorbing the force over a distance. Calculate the magnitude of the average force on a bumper that collapses 0.200 m while bringing a 900-kg car to rest from an initial speed of 1.1 m/s.
  5. Boxing gloves are padded to lessen the force of a blow. (a) Calculate the force exerted by a boxing glove on an opponent’s face, if the glove and face compress 7.50 cm during a blow in which the 7.00-kg arm and glove are brought to rest from an initial speed of 10.0 m/s. (b) Calculate the force exerted by an identical blow in the gory old days when no gloves were used and the knuckles and face would compress only 2.00 cm. (c) Discuss the magnitude of the force with glove on. Does it seem high enough to cause damage even though it is lower than the force with no glove?
  6. Using energy considerations, calculate the average force a 60.0-kg sprinter exerts backward on the track to accelerate from 2.00 to 8.00 m/s in a distance of 25.0 m, if he encounters a headwind that exerts an average force of 30.0 N against him.

Glossary

net work
work done by the net force, or vector sum of all the forces, acting on an object
work-energy theorem
the result, based on Newton’s laws, that the net work done on an object is equal to its change in kinetic energy
kinetic energy
the energy an object has by reason of its motion, equal to [latex]\frac{1}{2}{\text{mv}}^{2}[/latex] for the translational (i.e., non-rotational) motion of an object of mass [latex]m[/latex] moving at speed [latex]v[/latex]
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book