"

Fluid Statics

82 Cohesion and Adhesion in Liquids: Surface Tension and Capillary Action

Learning Objectives

  • Explain the role of cohesive and adhesive forces in fluid behavior.
  • Define and interpret surface tension in biological and physical contexts.
  • Describe capillary action and its relevance in biological systems.

Cohesion and Adhesion in Liquids

Whether it’s soap bubbles in the summer air or blood moving through capillaries, the microscopic interactions between molecules have macroscopic consequences. The behavior of liquids is largely governed by the forces between their molecules, and these forces are crucial in many biological and physiological processes.

When molecules of the same type attract each other, the resulting force is called a cohesive force. This force is what keeps water droplets intact and allows blood plasma to remain a continuous stream through vessels. On the other hand, the attraction between molecules of different types is known as an adhesive force. Adhesive forces help fluids like blood and mucus stick to vessel walls or epithelial tissues.

For example, when a healthcare worker draws blood using a capillary tube, adhesive forces between the blood and glass help pull the liquid into the tube. Simultaneously, cohesive forces within the blood help maintain the integrity of the sample.

The soap bubbles that the child blows into the air maintain their shape because of the attractive force between the molecules of the soap bubble.
Figure 82.1 Soap bubbles maintain their shape due to cohesive forces. The attraction between molecules in a liquid explains why bubbles form and why they retain their structure. (credit: Steve Ford Elliott)

Surface Tension

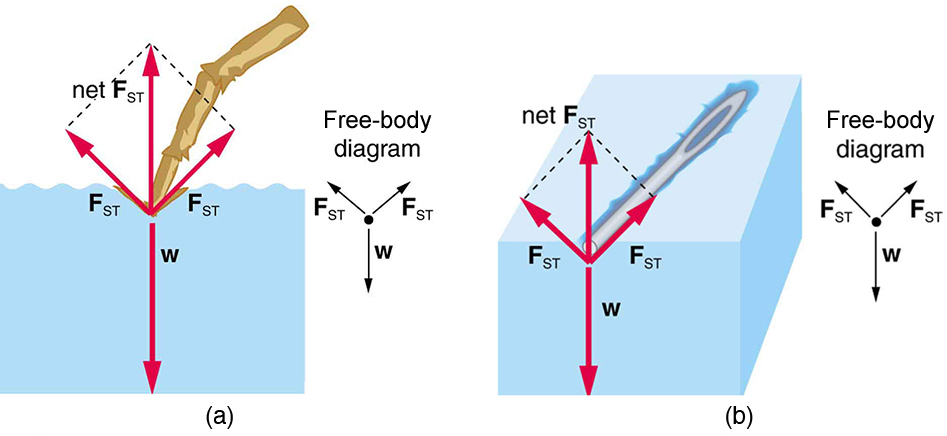
The tendency of a liquid’s surface to contract and minimize its area is known as surface tension. This is caused by cohesive forces pulling surface molecules inward, creating a surface that behaves like an elastic membrane (see Figure 82.2). Surface tension plays a crucial role in many biological systems, including the ability of some insects to walk on water and the function of alveoli in the lungs.

Within the bulk of a liquid, molecules experience balanced forces from their neighbors in all directions. However, molecules at the surface experience a net inward force, leading to surface contraction. This effect gives rise to the familiar spherical shape of small droplets and the resistance of the liquid surface to penetration.

The surface tension [latex]\gamma[/latex] is defined as the force per unit length:

[latex]\gamma = \frac{F}{L}[/latex]

where [latex]F[/latex] is the force acting along the surface and [latex]L[/latex] is the length over which it acts. Stronger cohesive forces result in higher surface tension, as illustrated in Table 82.1.

A leg of an insect resting on the water surface is shown in the first figure. In the second figure an iron needle rests on the surface of water without sinking. Both are possible due to the tension on the surface of the liquid.
Figure 82.2 Surface tension supports objects like an insect (a) or an iron needle (b). These are not floating but are supported by the tension of the liquid surface itself.

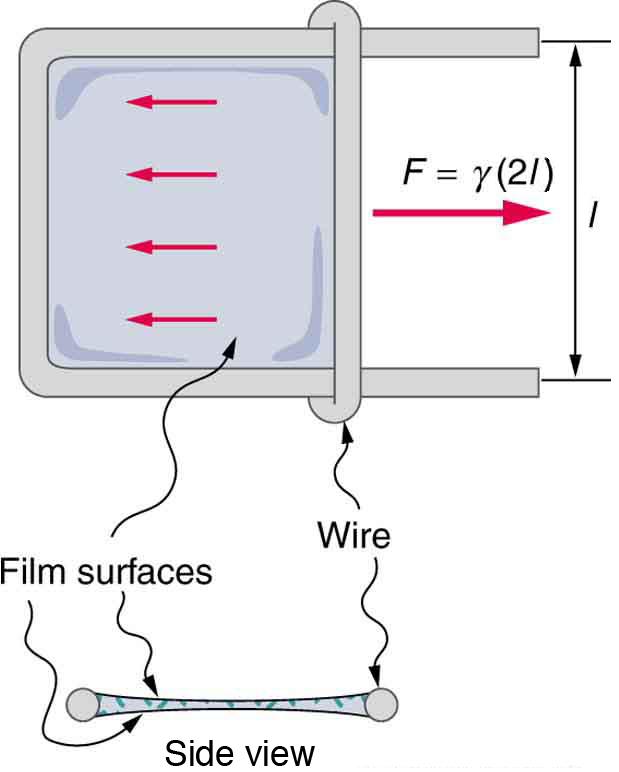
Surface tension can be measured using specialized instruments, such as a sliding wire frame. The force required to move the wire is proportional to surface tension and can be used for quantitative comparisons. An example is shown in Figure 82.3

Sliding wire device which is used to measure surface tension shows the force exerted on the two surfaces of the liquid. This force remains a constant until the film’s breaking point.
Figure 82.3 A sliding wire device for measuring surface tension. The film exerts a constant force until it breaks, which helps determine [latex]\gamma[/latex] for different liquids.

Surface Tension and Bubbles

Surface tension also explains why bubbles and droplets tend to be spherical. The internal pressure [latex]P[/latex] in a spherical bubble is related to surface tension by the equation:

[latex]P = \frac{4\gamma}{r}[/latex]

where [latex]r[/latex] is the radius of the bubble. This means smaller bubbles experience greater internal pressure. A practical example is shown in Figure 82.4, where air flows from a smaller balloon (higher internal pressure) to a larger one (lower pressure).

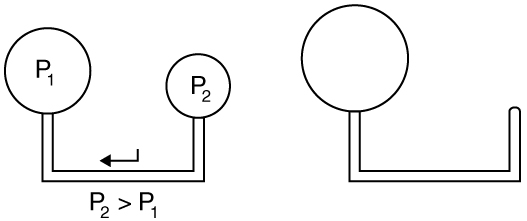
When two balloons are attached to the ends of a glass tube air flows from one to the other if their sizes are different.
Figure 82.4 Pressure differences due to surface tension cause air to move from a smaller balloon (higher internal pressure) into a larger one

Table of Surface Tension Values

Table 82.1 Surface Tension of Some Liquids1
Liquid Surface tension γ(N/m)
Water at [latex]0\text{º}\text{C}[/latex] 0.0756
Water at [latex]\text{20}\text{º}\text{C}[/latex] 0.0728
Water at [latex]\text{100}\text{º}\text{C}[/latex] 0.0589
Soapy water (typical) 0.0370
Ethyl alcohol 0.0223
Glycerin 0.0631
Mercury 0.465
Olive oil 0.032
Tissue fluids (typical) 0.050
Blood, whole at [latex]\text{37}\text{º}\text{C}[/latex] 0.058
Blood plasma at [latex]\text{37}\text{º}\text{C}[/latex] 0.073
Gold at [latex]\text{1070}\text{º}\text{C}[/latex] 1.000
Oxygen at [latex]-\text{193}\text{º}\text{C}[/latex] 0.0157
Helium at [latex]-\text{269}\text{º}\text{C}[/latex] 0.00012

Example 82.1 Surface Tension: Pressure Inside a Bubble

Calculate the gauge pressure inside a soap bubble [latex]2\text{.}\text{00}×{\text{10}}^{-4}\phantom{\rule{0.25em}{0ex}}\text{m}[/latex] in radius using the surface tension for soapy water in Table 82.1 . Convert this pressure to mm Hg.

Strategy

The radius is given and the surface tension can be found in Table 82.1 , and so [latex]P[/latex] can be found directly from the equation [latex]P=\frac{4\gamma }{r}[/latex].

Solution

Substituting [latex]r[/latex] and [latex]\gamma[/latex] into the equation [latex]P=\frac{4\gamma }{r}[/latex], we obtain

[latex]P=\frac{4\gamma }{r}=\frac{4\left(0.037 N/m\right)}{2\text{.}\text{00}×{\text{10}}^{-4}\phantom{\rule{0.25em}{0ex}}\text{m}}=\text{740}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}=\text{740}\phantom{\rule{0.25em}{0ex}}\text{Pa}.[/latex]

We use a conversion factor to get this into units of mm Hg:

[latex]P=\left(\text{740}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}\right)\frac{1.00 mm Hg}{\text{133}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}}=5.56 mm Hg.[/latex]

Discussion

Note that if a hole were to be made in the bubble, the air would be forced out, the bubble would decrease in radius, and the pressure inside would increase to atmospheric pressure (760 mm Hg).

Surface Tension in the Lungs and Capillary Action

Surface Tension and the Alveoli

Our lungs contain hundreds of millions of tiny, mucus-lined sacs called alveoli, each about 0.1 mm in diameter. These alveoli are the site of gas exchange, and they behave similarly to microscopic bubbles. The surface tension in the thin fluid layer lining each alveolus plays a crucial role in the mechanics of breathing (Figure 82.5).

During exhalation, this surface tension naturally contracts the alveoli, assisting with the expulsion of air without requiring muscular effort. In medical settings, patients using a positive-pressure respirator receive air pushed into the lungs, but exhalation often relies on this passive surface tension. Since pressure increases as alveolar radius decreases, an occasional deep breath is necessary to reinflate the alveoli—a pattern seen in both humans and animals like cats and dogs as they settle down to rest.

This image shows the bronchioles and alveolar sacs in the lungs and depicts the exchange of oxygenated and deoxygenated blood in the pulmonary blood vessels.
Figure 82.5 Bronchial tubes in the lungs branch into ever-smaller structures, ending in alveoli. The alveoli act like tiny bubbles. The surface tension of their mucous lining aids in exhalation and can also resist inhalation if too great.

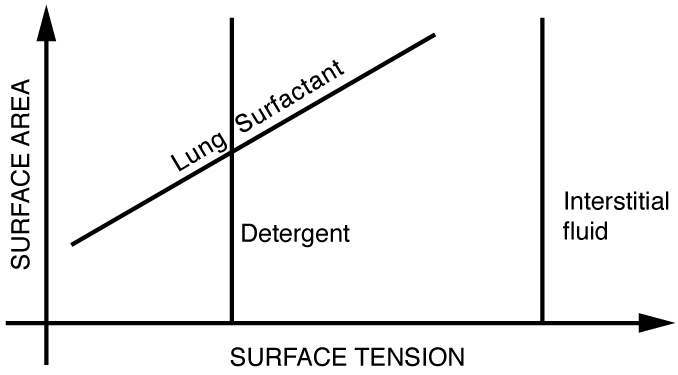
Each alveolus is lined with a thin fluid that contains a long lipoprotein molecule that serves as a surfactant—a substance that reduces surface tension. Without this surfactant, smaller alveoli would collapse and larger ones would grow even larger due to differences in pressure. During inhalation, the surfactant molecules are spread thin, increasing surface tension. During exhalation, the molecules pack more closely, reducing tension and preventing alveolar collapse. This dynamic tension response is unique to biological surfactants and is not shared by standard detergents (Figure 82.6).

Graph of surface tension as a function of surface area for detergents and interstitial fluids.
Figure 82.6 Surface tension as a function of surface area. For lung surfactants, surface tension decreases as area decreases, preventing collapse of small alveoli and over-expansion of large ones.

When water enters the lungs, surface tension becomes too strong to allow inhalation. This complicates resuscitation in drowning victims. A similar issue arises in premature infants born without surfactant. This condition, known as hyaline membrane disease, makes breathing very difficult and is a leading cause of neonatal death. Treatments often include spraying artificial surfactant into the infant’s lungs.

In contrast, emphysema leads to destruction of alveolar walls, causing sacs to merge into larger ones. Since the pressure from surface tension decreases as radius increases, these enlarged sacs produce less force to expel air, making exhalation difficult. Pulmonary function tests for emphysema often measure the pressure and volume of exhaled air.

Making Connections: Take-Home Investigation

  • Float a clean sewing needle on water. Why does it float despite being denser than water?
  • Dip a paintbrush in water and observe the bristles sticking together—how is this related to surface tension?
  • Place a loop of thread on water. Add a drop of detergent inside. What happens to the loop shape and why?
  • Sprinkle pepper on water. Add detergent. What happens to the pepper?
  • Float two matches parallel to each other. Add detergent between them. What happens and why?

Adhesion, Cohesion, and Capillary Action

Why does water bead up on waxed surfaces but spread out on bare paint? This phenomenon is explained by the interplay of cohesive and adhesive forces. The shape of a water droplet is determined by the contact angle [latex]\theta[/latex]—the angle between the tangent to the droplet’s surface and the solid surface (Figure 82.7).

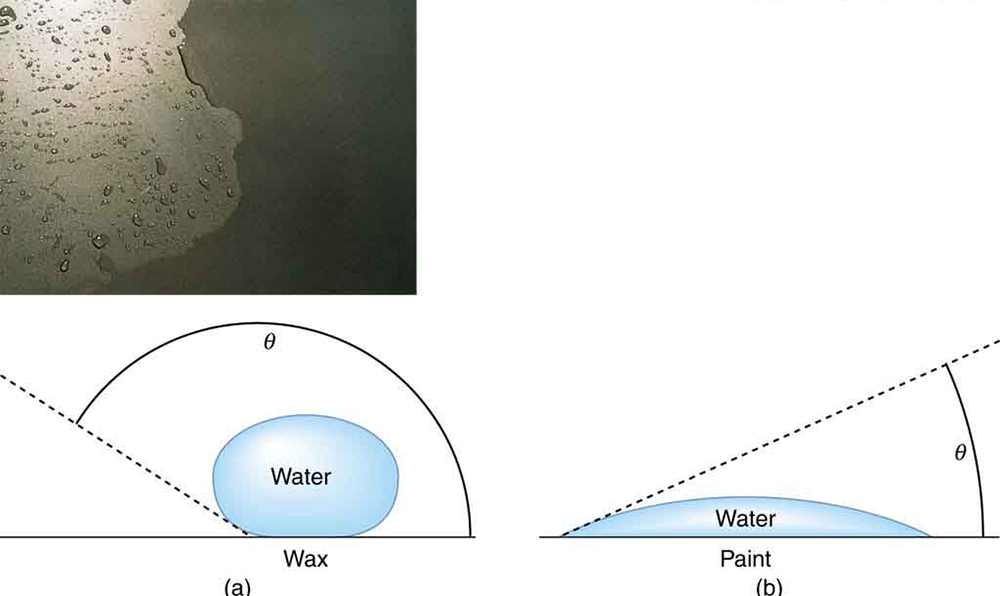
Water is seen to make beads on the waxed surface of car paint and it remains flat on the surface without wax. The beads are due to the greater force of attraction between the water molecules than between the water molecules and the surface. On the surface without wax the force of attraction between the water molecules and paint is greater.
Figure 82.7 (a) Water beads on wax due to strong cohesive forces. (b) On bare paint, adhesive forces dominate and flatten the droplet. The contact angle [latex]\theta[/latex] is an indicator of this balance. (credit: P. P. Urone)

Contact Angle

The angle [latex]\theta[/latex] between the tangent to the liquid surface and the surface is called the contact angle. A smaller [latex]\theta[/latex] indicates stronger adhesion, while a larger [latex]\theta[/latex] indicates stronger cohesion.

Capillary action is the rise or fall of a liquid in a narrow tube due to adhesion and surface tension. For example, blood is drawn into a fine capillary tube when the tube touches a droplet (Figure 82.8). Table 82.2 lists contact angles for several combinations of liquids and solids.

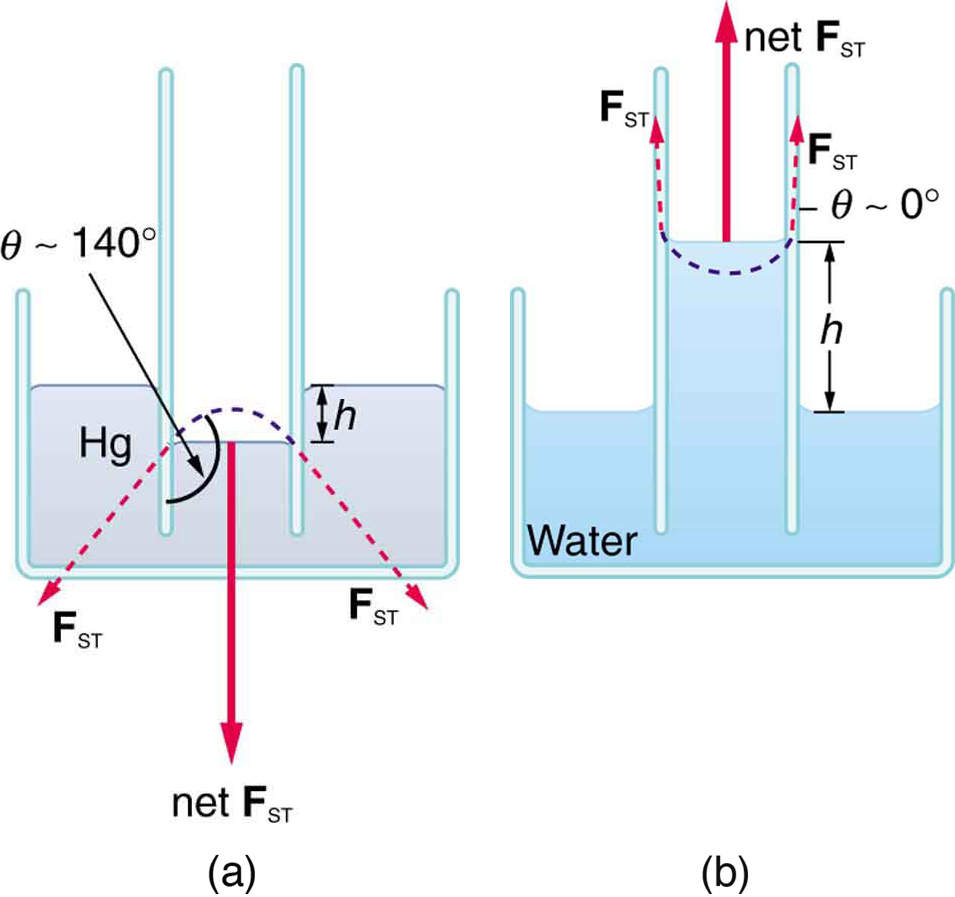
Mercury kept in a container into which a narrow tube is inserted lowers its level inside the tube relative to the level in the rest of the container. In a similar situation, water rises in the tube so that the water level in the tube is above the water level in the rest of the container. This phenomenon is due to the large contact angle of mercury with glass and the smaller contact angle of water with glass.
Figure 82.8 (a) Mercury is depressed in glass due to poor adhesion and a large contact angle. (b) Water rises due to strong adhesion and nearly zero contact angle.

Capillary Action

The tendency of a liquid to rise or fall in a narrow tube due to surface tension and adhesion is known as capillary action.

Whether the liquid rises or falls depends on [latex]\theta[/latex]. If [latex]\theta 90^\circ[/latex], the liquid rises. If [latex]\theta > 90^\circ[/latex], it is suppressed. This behavior is quantitatively described by the equation:

[latex]h = \frac{2\gamma \cos \theta}{\rho g r}[/latex]

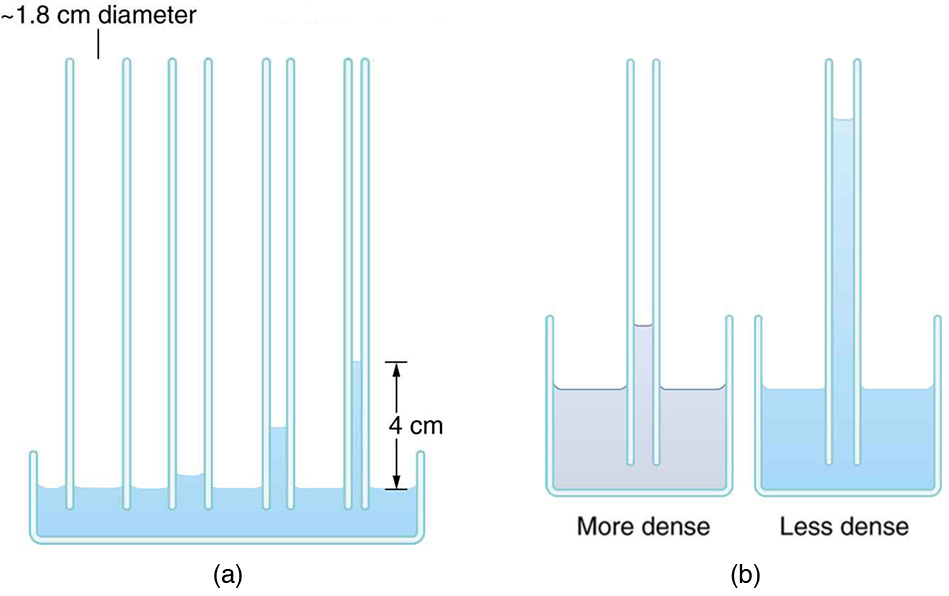
Here, [latex]h[/latex] is the height the fluid rises (or falls), [latex]\gamma[/latex] is surface tension, [latex]\rho[/latex] is the fluid’s density, [latex]g[/latex] is the acceleration due to gravity, and [latex]r[/latex] is the tube radius. As expected, smaller-radius tubes and lower-density fluids produce greater capillary rise (Figure 82.9).

The left image shows liquid in a container with four tubes of progressively smaller diameter inserted into the liquid. The liquid rises higher in the smaller-diameter tubes. The right image shows two containers, one holding a dense liquid and the other holding a less-dense liquid. Identical tubes are inserted into each liquid. The less-dense liquid rises higher in its tube than the more-dense liquid does in its tube.
Figure 82.9 (a) The smaller the tube radius, the higher the capillary rise. (b) Fluids with lower density rise higher in the same capillary tube.
Table 82.2 Contact Angles of Some Substances

Interface
Contact angle Θ

Mercury–glass
[latex]\text{140}\text{º}[/latex]

Water–glass
[latex]0\text{º}[/latex]

Water–paraffin
[latex]\text{107}\text{º}[/latex]

Water–silver
[latex]\text{90}\text{º}[/latex]

Organic liquids (most)–glass
[latex]0\text{º}[/latex]

Ethyl alcohol–glass
[latex]0\text{º}[/latex]

Kerosene–glass
[latex]\text{26}\text{º}[/latex]

 

Example 82.2 Calculating Radius of a Capillary Tube: Capillary Action: Tree Sap

Can capillary action be solely responsible for sap rising in trees? To answer this question, calculate the radius of a capillary tube that would raise sap 100 m to the top of a giant redwood, assuming that sap’s density is [latex]\text{1050 kg}{\text{/m}}^{3}[/latex], its contact angle is zero, and its surface tension is the same as that of water at [latex]20.0º C[/latex].

Strategy

The height to which a liquid will rise as a result of capillary action is given by [latex]h=\frac{2\gamma \phantom{\rule{0.25em}{0ex}}\text{cos}\phantom{\rule{0.25em}{0ex}}\theta }{\rho \text{gr}}[/latex], and every quantity is known except for [latex]r[/latex].

Solution

Solving for [latex]r[/latex] and substituting known values produces

[latex]\begin{array}{lll}r& =& \frac{2\gamma \phantom{\rule{0.25em}{0ex}}\text{cos}\phantom{\rule{0.25em}{0ex}}\theta }{\rho \text{gh}}=\frac{2\left(\text{0.0728 N/m}\right)\text{cos}\left(0º\right)}{\left(\text{1050}\phantom{\rule{0.25em}{0ex}}{\text{kg/m}}^{3}\right)\left(9\text{.}\text{80}\phantom{\rule{0.25em}{0ex}}{\text{m/s}}^{2}\right)\left(\text{100 m}\right)}\\ & =& 1.41×{\text{10}}^{-7}\phantom{\rule{0.25em}{0ex}}\text{m.}\end{array}[/latex]

Discussion

This result is unreasonable. Sap in trees moves through the xylem, which forms tubes with radii as small as [latex]2\text{.}5×{\text{10}}^{-5}\phantom{\rule{0.25em}{0ex}}\text{m}[/latex]. This value is about 180 times as large as the radius found necessary here to raise sap [latex]\text{100 m}[/latex]. This means that capillary action alone cannot be solely responsible for sap getting to the tops of trees.

Transpiration, Cohesion, and Sap Flow in Trees

A longstanding question in biology and plant physiology is: How does sap reach the tops of tall trees? After all, a column of water can only rise to about 10 meters under a perfect vacuum (see Example 78.3). Yet redwoods and tropical trees may reach over 100 meters tall. What mechanism allows this vertical transport of sap?

Although the full answer is still being investigated, the dominant explanation involves the cohesive forces between water molecules. Water is drawn up through the xylem in a continuous column, much like links in a chain. As water evaporates from leaves in a process called transpiration, it pulls on the column of water beneath it. This creates a negative pressure that effectively “pulls” sap upward, from roots to leaves.

In most fluid systems, pressure is exerted by pushing—pulling typically doesn’t work because the cohesive forces are too weak. However, water is an exception. Its strong hydrogen bonding provides sufficient cohesion to sustain negative pressures and prevent the water column from breaking. Figure 82.10 shows one device for studying negative pressure. Some experiments have demonstrated that negative pressures sufficient to pull sap to the tops of the tallest trees can be achieved.

When the piston is raised the liquid stretches somewhat, which results in negative pressure.
Figure 82.10 (a) Raising the piston stretches the liquid, placing it under tension and creating a negative absolute pressure given by [latex]P = -\frac{F}{A}[/latex]. (b) Eventually, the cohesive forces break down, and the liquid separates. This experiment provides insight into the limits of cohesion and the magnitude of negative pressures in liquids.

Such experiments support the idea that water can sustain enough tension to allow sap to rise to the top of the tallest trees, powered by evaporation at the leaf surface and cohesion within the water column.

Section Summary

  • Cohesive forces are the attractive interactions between molecules of the same substance (e.g., water–water).
  • Adhesive forces are the attractive interactions between molecules of different substances (e.g., water–glass).
  • Cohesive forces at the surface cause a liquid to contract to the smallest surface area possible, a phenomenon known as surface tension.
  • Capillary action is the rise or fall of a liquid in a narrow tube due to the balance between cohesive and adhesive forces.

Conceptual Questions

  1. The density of oil is less than that of water, yet a loaded oil tanker sits lower in the water than an empty one. Why?
  2. Is surface tension due to cohesive or adhesive forces, or both?
  3. Is capillary action due to cohesive or adhesive forces, or both?
  4. Birds such as ducks, geese, and swans have greater densities than water, yet they are able to sit on its surface. Explain this ability, noting that water does not wet their feathers and that they cannot sit on soapy water.
  5. Water beads up on an oily sunbather, but not on her neighbor, whose skin is not oiled. Explain in terms of cohesive and adhesive forces.
  6. Could capillary action be used to move fluids in a “weightless” environment, such as in an orbiting space probe?
  7. What effect does capillary action have on the reading of a manometer with uniform diameter? Explain your answer.
  8. Pressure between the inside chest wall and the outside of the lungs normally remains negative. Explain how pressure inside the lungs can become positive (to cause exhalation) without muscle action.

Problems & Exercises

  1. What is the pressure inside an alveolus having a radius of [latex]2\text{.}\text{50}×{\text{10}}^{-4}\phantom{\rule{0.25em}{0ex}}\text{m}[/latex] if the surface tension of the fluid-lined wall is the same as for soapy water? You may assume the pressure is the same as that created by a spherical bubble.
  2. (a) The pressure inside an alveolus with a [latex]2\text{.}\text{00}×{\text{10}}^{-4}[/latex]-m radius is [latex]1\text{.}\text{40}×{\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}\text{Pa}[/latex], due to its fluid-lined walls. Assuming the alveolus acts like a spherical bubble, what is the surface tension of the fluid? (b) Identify the likely fluid. (You may need to extrapolate between values in Table 82.2.)
  3. What is the gauge pressure in millimeters of mercury inside a soap bubble 0.100 m in diameter?
  4. Calculate the force on the slide wire in Figure 82.3 if it is 3.50 cm long and the fluid is ethyl alcohol.
  5. Figure 82.9(a) shows the effect of tube radius on the height to which capillary action can raise a fluid. (a) Calculate the height [latex]h[/latex] for water in a glass tube with a radius of 0.900 cm—a rather large tube like the one on the left. (b) What is the radius of the glass tube on the right if it raises water to 4.00 cm?
  6. We stated in Example 82.2that a xylem tube is of radius [latex]2\text{.}\text{50}×{\text{10}}^{-5}\phantom{\rule{0.25em}{0ex}}\text{m}[/latex]. Verify that such a tube raises sap less than a meter by finding [latex]h[/latex] for it, making the same assumptions that sap’s density is [latex]\text{1050}\phantom{\rule{0.25em}{0ex}}{\text{kg/m}}^{3}[/latex], its contact angle is zero, and its surface tension is the same as that of water at [latex]20.0º C[/latex].
  7. What fluid is in the device shown in Figure 82.3 if the force is [latex]3\text{.}\text{16}×{\text{10}}^{-3}\phantom{\rule{0.25em}{0ex}}\text{N}[/latex] and the length of the wire is 2.50 cm? Calculate the surface tension [latex]\gamma[/latex] and find a likely match from Table 82.2.
  8. If the gauge pressure inside a rubber balloon with a 10.0-cm radius is 1.50 cm of water, what is the effective surface tension of the balloon?
  9. Calculate the gauge pressures inside 2.00-cm-radius bubbles of water, alcohol, and soapy water. Which liquid forms the most stable bubbles, neglecting any effects of evaporation?
  10. Suppose water is raised by capillary action to a height of 5.00 cm in a glass tube. (a) To what height will it be raised in a paraffin tube of the same radius? (b) In a silver tube of the same radius?
  11. Calculate the contact angle [latex]\theta[/latex] for olive oil if capillary action raises it to a height of 7.07 cm in a glass tube with a radius of 0.100 mm. Is this value consistent with that for most organic liquids?
  12. When two soap bubbles touch, the larger is inflated by the smaller until they form a single bubble. (a) What is the gauge pressure inside a soap bubble with a 1.50-cm radius? (b) Inside a 4.00-cm-radius soap bubble? (c) Inside the single bubble they form if no air is lost when they touch?
  13. Calculate the ratio of the heights to which water and mercury are raised by capillary action in the same glass tube.
  14. The ratio is negative because water is raised whereas mercury is lowered.
  15. What is the ratio of heights to which ethyl alcohol and water are raised by capillary action in the same glass tube?

Footnotes

  1. 1 At 20ºC unless otherwise stated.

Glossary

adhesive forces
the attractive forces between molecules of different types
capillary action
the tendency of a fluid to be raised or lowered in a narrow tube
cohesive forces
the attractive forces between molecules of the same type
contact angle
the angle [latex]\theta[/latex] between the tangent to the liquid surface and the surface
surface tension
the cohesive forces between molecules which cause the surface of a liquid to contract to the smallest possible surface area
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book