"

Fluid Statics

78 Variation of Pressure with Depth in a Fluid

Learning Objectives

  • Define pressure in terms of the weight of a fluid.
  • Explain how pressure varies with depth in a fluid.
  • Calculate fluid density using pressure and depth or altitude data.

If you’ve ever felt your ears pop during a flight or while diving underwater, you’ve experienced the physiological effects of pressure changes with depth. These changes occur because pressure in a fluid increases with depth due to the increasing weight of fluid above. At sea level, atmospheric pressure results from the weight of the column of air above you. Underwater, pressure increases more rapidly, as both the atmosphere and the water above contribute to the total pressure—and water is about 775 times denser than air. This is why a one-meter dive can be felt more immediately than a 10-story elevator ride.

Pressure Due to Fluid Weight

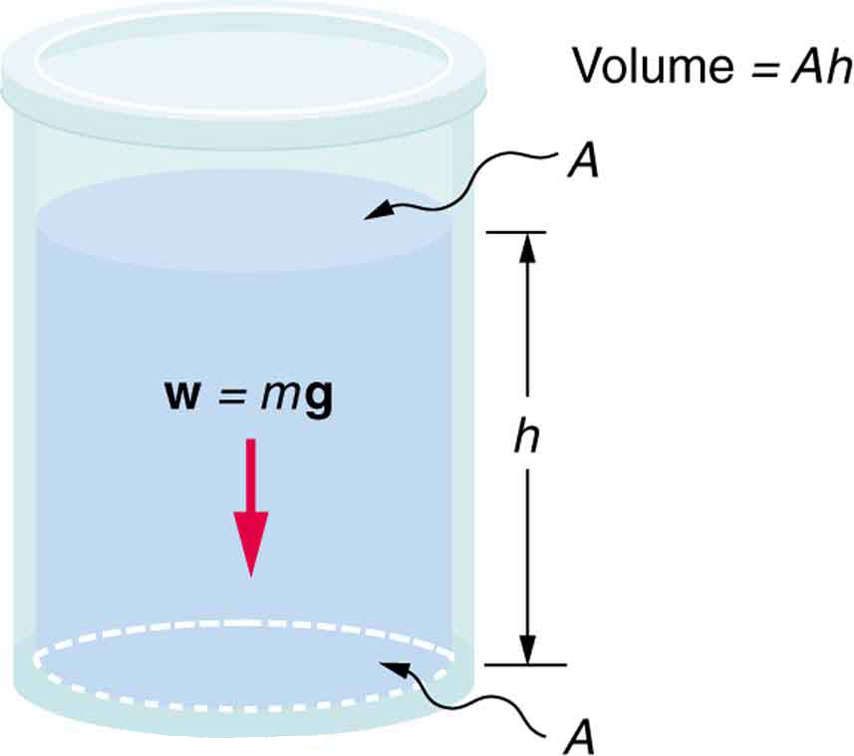
To understand how pressure arises from the weight of a fluid, consider the fluid in a container as shown in Figure 78.1. The pressure at the bottom of the container is due to the weight of the fluid resting on the area of the base:

[latex]P = \frac{mg}{A}[/latex]

Here, [latex]m[/latex] is the mass of the fluid, [latex]g[/latex] is the acceleration due to gravity, and [latex]A[/latex] is the area of the container’s base. Substituting [latex]m = \rho V[/latex], where [latex]\rho[/latex] is the fluid density and [latex]V[/latex] is the volume:

[latex]V = Ah[/latex]

So the mass becomes:

[latex]m = \rho A h[/latex]

Substituting back into the pressure equation:

[latex]P = \frac{\rho A h g}{A} = \rho g h[/latex]

This relationship tells us that the pressure at a depth [latex]h[/latex] in a fluid is proportional to the fluid’s density and the depth itself:

[latex]P = \rho g h[/latex]

This formula is valid for any fluid with average density [latex]\rho[/latex] at depth [latex]h[/latex], provided the fluid is either incompressible (like most liquids) or compressibility effects are negligible (as in shallow regions of the atmosphere).

A container with fluid filled to a depth h. The fluid’s weight w equal to m times g is shown by an arrow pointing downward. A denotes the area of the fluid at the bottom of the container and as well as on the surface.
Figure 78.1 The bottom of this container supports the entire weight of the fluid. The sides provide no upward support because fluids do not resist shearing forces.

Example 78.1: Pressure on a Dam

A reservoir behind a dam holds water 80.0 m deep. The dam is 500 m wide. (a) What is the average pressure exerted by the water on the dam? (b) What total force does the water exert on the dam wall?

(a) Average Pressure

Using the midpoint depth (40.0 m) to find average pressure:

[latex]\overline{P} = \rho g \overline{h} = (1000\ \text{kg/m}^3)(9.80\ \text{m/s}^2)(40.0\ \text{m}) = 3.92 \times 10^5\ \text{Pa}[/latex]

(b) Force on the Dam

Area of the dam face:

[latex]A = (80.0\ \text{m})(500\ \text{m}) = 4.00 \times 10^4\ \text{m}^2[/latex]

Total force:

[latex]F = \overline{P} A = (3.92 \times 10^5\ \text{Pa})(4.00 \times 10^4\ \text{m}^2) = 1.57 \times 10^{10}\ \text{N}[/latex]

Though this is a large force, it is small compared to the weight of the water behind the dam, which is about [latex]1.96 \times 10^{13}\ \text{N}[/latex].

A two-dimensional view of a dam with dimensions L and h is shown. Force F at h is shown by a horizontal arrow. The force F exerted by water on the dam is F equals average pressure p bar into area A and pressure in turn is average height h bar into density rho into acceleration due to gravity g.
Figure 78.2 Water pressure increases with depth. The dam must withstand a greater force near the base, hence its thickened structure.

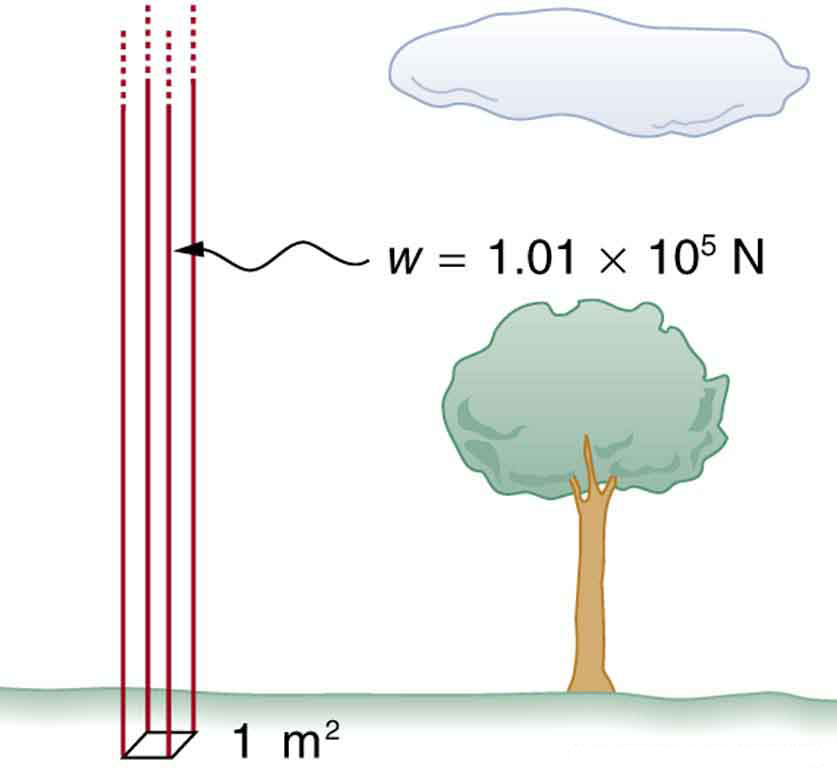
Atmospheric Pressure

Air exerts pressure due to its weight. At sea level, the average atmospheric pressure is:

[latex]P_{\text{atm}} = 1.01 \times 10^5\ \text{Pa} = 101\ \text{kPa}[/latex]

This is equivalent to the weight of a column of air 1 m² in cross-sectional area extending to the top of the atmosphere.

Figure shows a column of air exerting a weight of one point zero one times ten to the power five newtons on a rectangular patch of ground of one square meter cross section.
Figure 78.3 Atmospheric pressure at sea level is caused by the weight of a tall column of air above a given surface area.

Example 78.2: Average Density of Air

Estimate the average density of the atmosphere, assuming it extends 120 km above Earth’s surface.

[latex]\overline{\rho} = \frac{P}{hg} = \frac{1.01 \times 10^5}{(1.20 \times 10^5)(9.80)} = 8.59 \times 10^{-2}\ \text{kg/m}^3[/latex]

This average density is much lower than the air density at sea level (about 1.29 kg/m³) because air density drops rapidly with altitude due to compressibility.

Example 78.3: Depth Equivalent to Atmospheric Pressure

How deep below the surface of water do you need to go to experience a pressure of 1 atm?

[latex]h = \frac{P}{\rho g} = \frac{1.01 \times 10^5}{(1000)(9.80)} = 10.3\ \text{m}[/latex]

This means that just 10.3 meters of water exerts the same pressure as the entire Earth’s atmosphere. Therefore, at a depth of 10.3 m underwater, the total pressure experienced is 2 atm: 1 atm from the air above the surface and 1 atm from the water above that point.

Section Summary

  • Pressure due to the weight of a fluid is given by:
    [latex]P = \frac{mg}{A}[/latex]
  • Using volume and density, the pressure becomes:
    [latex]P = \rho g h[/latex]
  • Atmospheric pressure at sea level is approximately:
    [latex]P_{\text{atm}} = 1.01 \times 10^5\ \text{Pa} = 101\ \text{kPa}[/latex]

Conceptual Questions

  1. Atmospheric pressure exerts a large force (equal to the weight of the atmosphere above your body—about 10 tons) on the top of your body when you are lying on the beach sunbathing. Why are you able to get up?
  2. Why does atmospheric pressure decrease more rapidly than linearly with altitude?
  3. What are two reasons why mercury rather than water is used in barometers?
  4. Figure 78.4 shows how sandbags placed around a leak outside a river levee can effectively stop the flow of water under the levee. Explain how the small amount of water inside the column formed by the sandbags is able to balance the much larger body of water behind the levee.
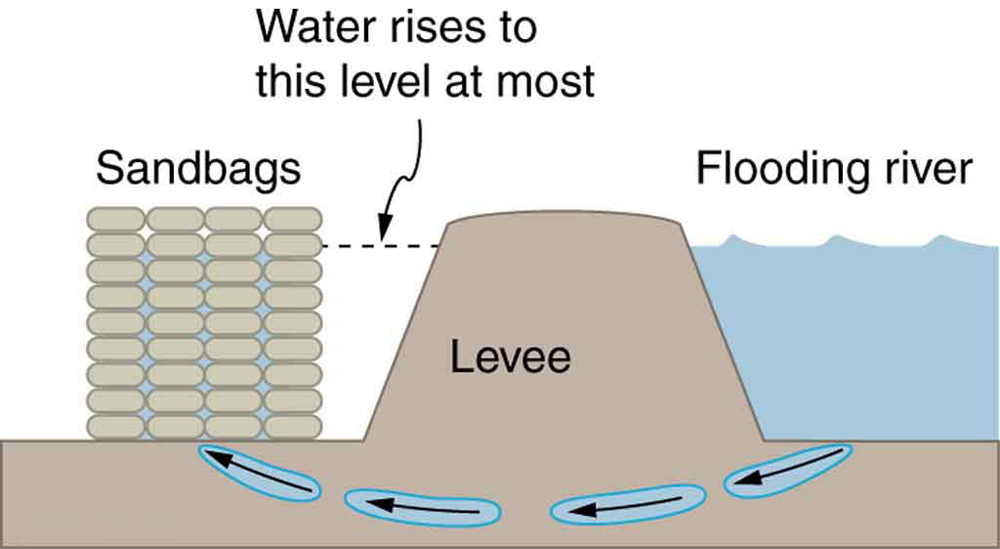
    The figure shows a flooding river on the extreme right, with a levee set up on its left, and sandbags are stacked on the left of the levee. The height of the levee and that of the stacked sandbags is greater than the water level of the flooding river, so the water does not flow over their tops, but a leak under the levee allows some water to flow under it and reach the sandbags.
    Figure 78.4 Because the river level is very high, it has started to leak under the levee. Sandbags are placed around the leak, and the water held by them rises until it is the same level as the river, at which point the water there stops rising.
  5. Why is it difficult to swim under water in the Great Salt Lake?
  6. Is there a net force on a dam due to atmospheric pressure? Explain your answer.
  7. Does atmospheric pressure add to the gas pressure in a rigid tank? In a toy balloon? When, in general, does atmospheric pressure not affect the total pressure in a fluid?
  8. You can break a strong wine bottle by pounding a cork into it with your fist, but the cork must press directly against the liquid filling the bottle—there can be no air between the cork and liquid. Explain why the bottle breaks, and why it will not if there is air between the cork and liquid.

Problems & Exercises

  1. What depth of mercury creates a pressure of 1.00 atm?
  2. The greatest ocean depths on the Earth are found in the Marianas Trench near the Philippines. Calculate the pressure due to the ocean at the bottom of this trench, given its depth is 11.0 km and assuming the density of seawater is constant all the way down.
  3. Verify that the SI unit of [latex]\mathrm{h\rho g}[/latex] is [latex]{\text{N/m}}^{2}[/latex].
  4. Water towers store water above the level of consumers for times of heavy use, eliminating the need for high-speed pumps. How high above a user must the water level be to create a gauge pressure of [latex]3\text{.}\text{00}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}[/latex]?
  5. The aqueous humor in a person’s eye is exerting a force of 0.300 N on the [latex]1\text{.}\text{10}{\text{-cm}}^{2}[/latex] area of the cornea. (a) What pressure is this in mm Hg? (b) Is this value within the normal range for pressures in the eye?
  6. How much force is exerted on one side of an 8.50 cm by 11.0 cm sheet of paper by the atmosphere? How can the paper withstand such a force?
  7. What pressure is exerted on the bottom of a 0.500-m-wide by 0.900-m-long gas tank that can hold 50.0 kg of gasoline by the weight of the gasoline in it when it is full?
  8. Calculate the average pressure exerted on the palm of a shot-putter’s hand by the shot if the area of contact is [latex]\text{50}\text{.}0\phantom{\rule{0.25em}{0ex}}{\text{cm}}^{2}[/latex] and he exerts a force of 800 N on it. Express the pressure in [latex]{\text{N/m}}^{2}[/latex] and compare it with the [latex]1\text{.}\text{00}×{\text{10}}^{6}\phantom{\rule{0.25em}{0ex}}\text{Pa}[/latex] pressures sometimes encountered in the skeletal system.
  9. The left side of the heart creates a pressure of 120 mm Hg by exerting a force directly on the blood over an effective area of [latex]\text{15}\text{.}0\phantom{\rule{0.25em}{0ex}}{\text{cm}}^{2}.[/latex] What force does it exert to accomplish this?
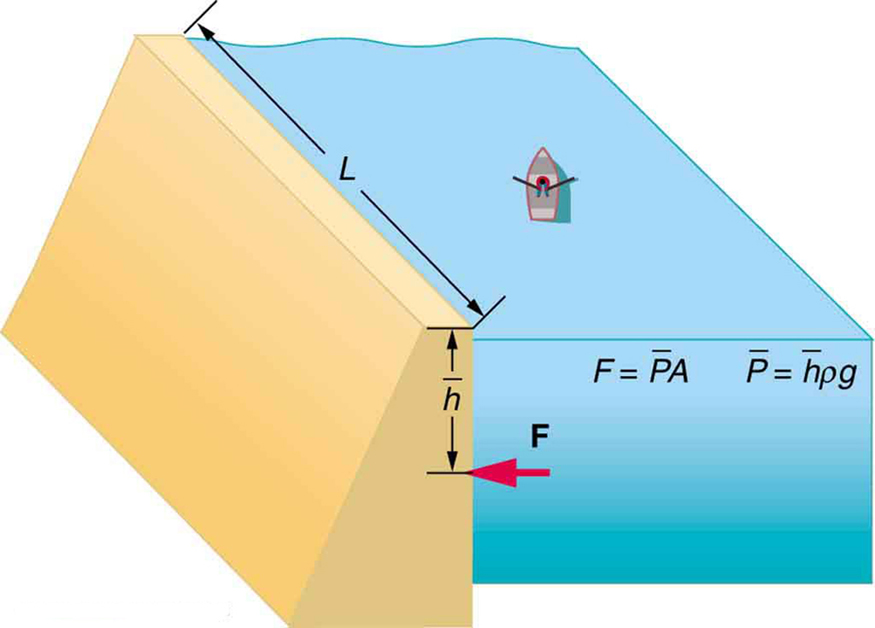
  10. Show that the total force on a rectangular dam due to the water behind it increases with the square of the water depth. In particular, show that this force is given by [latex]F=\rho {\mathrm{gh}}^{2}L/2[/latex], where [latex]\rho[/latex] is the density of water, [latex]h[/latex] is its depth at the dam, and [latex]L[/latex] is the length of the dam. You may assume the face of the dam is vertical. (Hint: Calculate the average pressure exerted and multiply this by the area in contact with the water. (See Figure 78.2.)

Glossary

pressure
the weight of the fluid divided by the area supporting it
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book