Work, Energy, and Energy Resources
49 Work, Energy, and Power in Humans
Learning Objectives
-
Explain the human body’s consumption of energy when at rest versus when engaged in activities that do useful work.
-
Calculate the conversion of chemical energy in food into useful work.
The Body as an Energy Conversion System
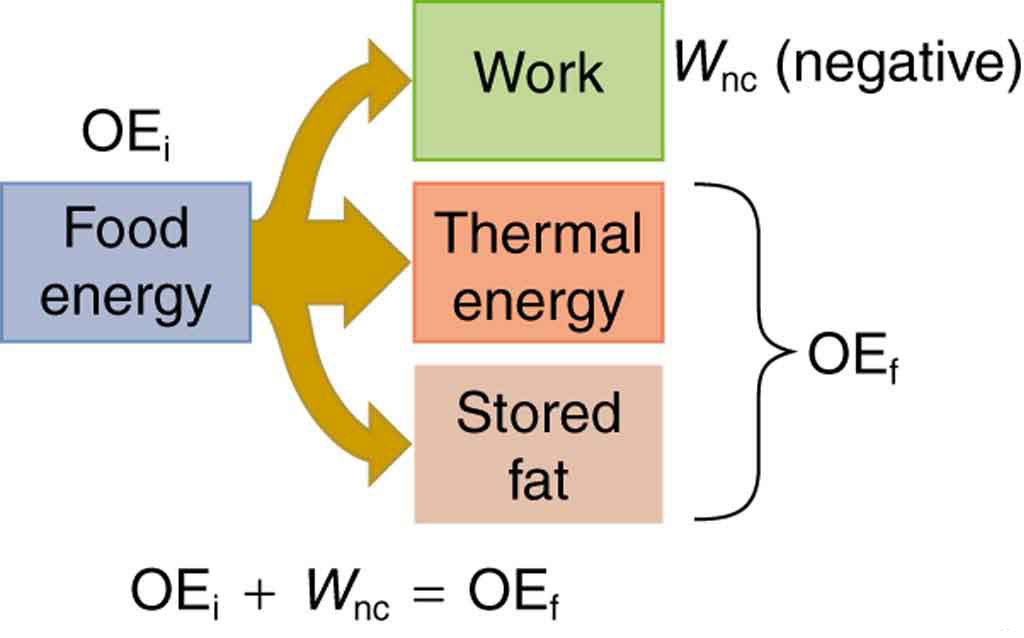
The human body is a complex energy conversion machine. According to the law of conservation of energy, the chemical energy stored in food must be converted into other forms: primarily thermal energy (heat), mechanical energy (doing work), and stored chemical energy in body fat. How energy is distributed depends on diet, metabolism, and physical activity (See Figure 49.1.).
Power Consumed at Rest: Basal Metabolic Rate
The rate at which the body converts energy when at rest is called the basal metabolic rate (BMR) as shown in Table 49.1. This represents the minimal energy expenditure required to sustain essential physiological functions: circulation, respiration, cellular maintenance, and organ function.
Metabolic energy expenditure is often measured in watts (W), where 1 W = 1 J/s. It is also directly related to oxygen consumption: about 20 kJ of energy are released per liter of O₂ consumed, regardless of food type.
.
Basal metabolic rate depends on several factors:
-
Age – BMR generally declines with age.
-
Sex – Males typically have higher BMRs due to greater muscle mass.
-
Body composition – Muscle tissue consumes more energy at rest than fat tissue.
Energy and Oxygen: A Biological Link
Because digestion is an oxidative process, we can estimate energy expenditure by measuring oxygen uptake. The average conversion is:
This relationship forms the basis for metabolic rate testing, fitness assessments, and sports physiology. We can measure the energy people use during various activities by measuring their oxygen use. (See Figure 49.2.) Approximately 20 kJ of energy are produced for each liter of oxygen consumed, independent of the type of food. Table 49.2 shows energy and oxygen consumption rates (power expended) for a variety of activities.
Energy consumption is directly proportional to oxygen consumption because the digestive process is basically one of oxidizing food.
| Activity | Energy consumption in watts | Oxygen consumption in liters O2/min |
|---|---|---|
| Sleeping | 83 | 0.24 |
| Sitting at rest | 120 | 0.34 |
| Standing relaxed | 125 | 0.36 |
| Sitting in class | 210 | 0.60 |
| Walking (5 km/h) | 280 | 0.80 |
| Cycling (13–18 km/h) | 400 | 1.14 |
| Shivering | 425 | 1.21 |
| Playing tennis | 440 | 1.26 |
| Swimming breaststroke | 475 | 1.36 |
| Ice skating (14.5 km/h) | 545 | 1.56 |
| Climbing stairs (116/min) | 685 | 1.96 |
| Cycling (21 km/h) | 700 | 2.00 |
| Running cross-country | 740 | 2.12 |
| Playing basketball | 800 | 2.28 |
| Cycling, professional racer | 1855 | 5.30 |
| Sprinting | 2415 | 6.90 |
Power of Useful Work
“Useful work“ refers to mechanical work performed on the environment, such as lifting, running, or climbing. This is distinct from internal work (e.g., pumping blood or digesting food).
Work is defined as a force applied through a distance:
Power is the rate at which work is performed:
In these activities, the human body acts via nonconservative forces, converting internal chemical energy (from food) into mechanical energy:
This energy transfer occurs in the external system where physical work is done.
Burning Calories with Work
When caloric intake exceeds energy use, the surplus is stored as fat. Physical activity increases energy demands and may draw on these energy reserves.
For instance, vigorous activity like running or cycling requires hundreds of kilocalories per hour. To burn just one pound of fat (approximately 3500 kcal), a person might need:
Thus, weight management involves both caloric intake and energy output—a principle rooted in the conservation of energy.
Example 49.1: Calculating Weight Loss from Exercising
If a person who normally requires an average of 12,000 kJ (3000 kcal) of food energy per day consumes 13,000 kJ per day, he will steadily gain weight. How much bicycling per day is required to work off this extra 1000 kJ?
Solution
Table 49.2 states that 400 W are used when cycling at a moderate speed. The time required to work off 1000 kJ at this rate is then
Discussion
If this person uses more energy than he or she consumes, the person’s body will obtain the needed energy by metabolizing body fat. If the person uses 13,000 kJ but consumes only 12,000 kJ, then the amount of fat loss will be
assuming the energy content of fat to be 39 kJ/g.
Energy Use in the Human Body
All bodily functions (See Figure 49.3.)—from conscious activities like lifting and running to automatic processes like thinking, digestion, and maintaining heart rhythm—require energy. These energy demands reflect the human body’s role as a highly complex energy conversion system.
Even while at rest, the body is constantly using energy. Seemingly simple actions—such as blinking, breathing, or shifting posture—involve small muscle contractions that ultimately dissipate as thermal energy. Internal organs like the heart, liver, and kidneys are also continuously active, performing life-sustaining work.
Interestingly, about 25% of your total energy consumption is used to maintain electrical potentials across cell membranes, a vital process for nerve impulses, muscle contractions, and intracellular signaling. This bioelectrical energy drives numerous chemical reactions throughout the body. While much of this energy ultimately converts to thermal energy, a portion powers cellular processes like protein synthesis, tissue repair, and detoxification.
One striking example of involuntary energy use is shivering. In cold conditions, muscles contract rhythmically without producing external work. This mechanical activity increases internal heat, helping maintain core body temperature—a perfect illustration of energy being used only to generate thermal energy without doing mechanical work
Section Summary
- The human body converts the chemical energy stored in food into mechanical work, thermal energy, and/or stored fat.
- The metabolic rate describes how quickly the body uses food energy, with the basal metabolic rate (BMR) referring to the rate at rest.
- Approximately 75% of daily caloric intake supports the body’s basal metabolic needs—including liver, brain, heart, and kidney function.
- Energy consumption during activity can be estimated using oxygen consumption, since food metabolism is fundamentally an oxidation process.
Conceptual Questions
- Explain why it is easier to climb a mountain on a zigzag path rather than one straight up the side. Is your increase in gravitational potential energy the same in both cases? Is your energy consumption the same in both?
- Do you do work on the outside world when you rub your hands together to warm them? What is the efficiency of this activity?
- Shivering is an involuntary response to lowered body temperature. What is the efficiency of the body when shivering, and is this a desirable value?
- Discuss the relative effectiveness of dieting and exercise in losing weight, noting that most athletic activities consume food energy at a rate of 400 to 500 W, while a single cup of yogurt can contain 1360 kJ (325 kcal). Specifically, is it likely that exercise alone will be sufficient to lose weight? You may wish to consider that regular exercise may increase the metabolic rate, whereas protracted dieting may reduce it.
Problems & Exercises
- (a) How long can you rapidly climb stairs (116/min) on the 93.0 kcal of energy in a 10.0-g pat of butter? (b) How many flights is this if each flight has 16 stairs?
- (a) What is the power output in watts and horsepower of a 70.0-kg sprinter who accelerates from rest to 10.0 m/s in 3.00 s? (b) Considering the amount of power generated, do you think a well-trained athlete could do this repetitively for long periods of time?
- Calculate the power output in watts and horsepower of a shot-putter who takes 1.20 s to accelerate the 7.27-kg shot from rest to 14.0 m/s, while raising it 0.800 m. (Do not include the power produced to accelerate his body.)
- (a) What is the efficiency of an out-of-condition professor who does [latex]2\text{.}\text{10}×{\text{10}}^{5}\text{ J}[/latex] of useful work while metabolizing 500 kcal of food energy? (b) How many food calories would a well-conditioned athlete metabolize in doing the same work with an efficiency of 20%?
- Energy that is not utilized for work or heat transfer is converted to the chemical energy of body fat containing about 39 kJ/g. How many grams of fat will you gain if you eat 10,000 kJ (about 2500 kcal) one day and do nothing but sit relaxed for 16.0 h and sleep for the other 8.00 h? Use data from Table 49.2 for the energy consumption rates of these activities.
- Using data from Table 49.2, calculate the daily energy needs of a person who sleeps for 7.00 h, walks for 2.00 h, attends classes for 4.00 h, cycles for 2.00 h, sits relaxed for 3.00 h, and studies for 6.00 h. (Studying consumes energy at the same rate as sitting in class.)
- What is the efficiency of a subject on a treadmill who puts out work at the rate of 100 W while consuming oxygen at the rate of 2.00 L/min? (Hint: See Table 49.2.)
- Shoveling snow can be extremely taxing because the arms have such a low efficiency in this activity. Suppose a person shoveling a footpath metabolizes food at the rate of 800 W. (a) What is her useful power output? (b) How long will it take her to lift 3000 kg of snow 1.20 m? (This could be the amount of heavy snow on 20 m of footpath.) (c) How much waste heat transfer in kilojoules will she generate in the process?
- Very large forces are produced in joints when a person jumps from some height to the ground. (a) Calculate the magnitude of the force produced if an 80.0-kg person jumps from a 0.600–m-high ledge and lands stiffly, compressing joint material 1.50 cm as a result. (Be certain to include the weight of the person.) (b) In practice the knees bend almost involuntarily to help extend the distance over which you stop. Calculate the magnitude of the force produced if the stopping distance is 0.300 m. (c) Compare both forces with the weight of the person.
- Jogging on hard surfaces with insufficiently padded shoes produces large forces in the feet and legs. (a) Calculate the magnitude of the force needed to stop the downward motion of a jogger’s leg, if his leg has a mass of 13.0 kg, a speed of 6.00 m/s, and stops in a distance of 1.50 cm. (Be certain to include the weight of the 75.0-kg jogger’s body.) (b) Compare this force with the weight of the jogger.
- (a) Calculate the energy in kJ used by a 55.0-kg woman who does 50 deep knee bends in which her center of mass is lowered and raised 0.400 m. (She does work in both directions.) You may assume her efficiency is 20%. (b) What is the average power consumption rate in watts if she does this in 3.00 min?
- Kanellos Kanellopoulos flew 119 km from Crete to Santorini, Greece, on April 23, 1988, in the Daedalus 88, an aircraft powered by a bicycle-type drive mechanism (see Figure 49.5). His useful power output for the 234-min trip was about 350 W. Using the efficiency for cycling from Table 47.2, calculate the food energy in kilojoules he metabolized during the flight.

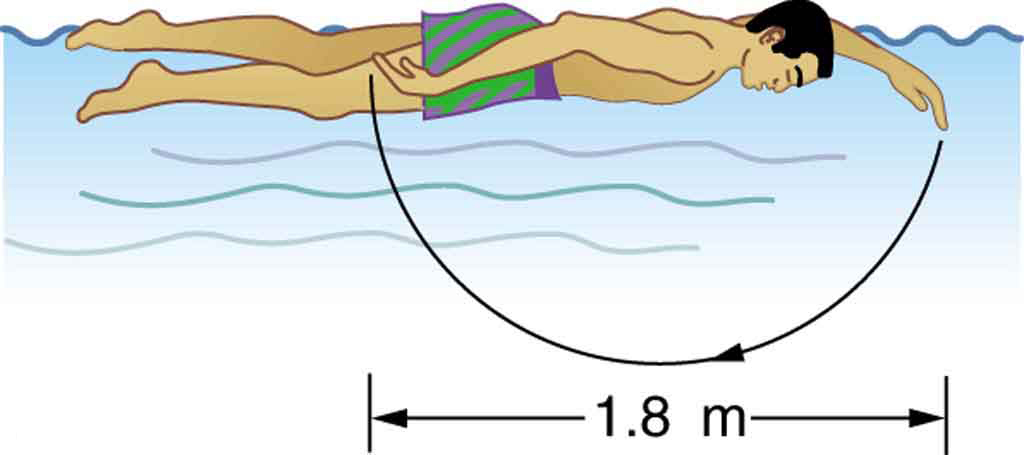
Figure 49.5: The Daedalus 88 in flight. (credit: NASA photo by Beasley) - The swimmer shown in Figure 49.6 exerts an average horizontal backward force of 80.0 N with his arm during each 1.80 m long stroke. (a) What is his work output in each stroke? (b) Calculate the power output of his arms if he does 120 strokes per minute.
- Mountain climbers carry bottled oxygen when at very high altitudes. (a) Assuming that a mountain climber uses oxygen at twice the rate for climbing 116 stairs per minute (because of low air temperature and winds), calculate how many liters of oxygen a climber would need for 10.0 h of climbing. (These are liters at sea level.) Note that only 40% of the inhaled oxygen is utilized; the rest is exhaled. (b) How much useful work does the climber do if he and his equipment have a mass of 90.0 kg and he gains 1000 m of altitude? (c) What is his efficiency for the 10.0-h climb?
- The awe-inspiring Great Pyramid of Cheops was built more than 4500 years ago. Its square base, originally 230 m on a side, covered 13.1 acres, and it was 146 m high, with a mass of about [latex]7×{10}^{9}\phantom{\rule{0.25em}{0ex}}\text{kg}[/latex]. (The pyramid’s dimensions are slightly different today due to quarrying and some sagging.) Historians estimate that 20,000 workers spent 20 years to construct it, working 12-hour days, 330 days per year. (a) Calculate the gravitational potential energy stored in the pyramid, given its center of mass is at one-fourth its height. (b) Only a fraction of the workers lifted blocks; most were involved in support services such as building ramps (see Figure 49.7), bringing food and water, and hauling blocks to the site. Calculate the efficiency of the workers who did the lifting, assuming there were 1000 of them and they consumed food energy at the rate of 300 kcal/h. What does your answer imply about how much of their work went into block-lifting, versus how much work went into friction and lifting and lowering their own bodies? (c) Calculate the mass of food that had to be supplied each day, assuming that the average worker required 3600 kcal per day and that their diet was 5% protein, 60% carbohydrate, and 35% fat. (These proportions neglect the mass of bulk and nondigestible materials consumed.)
Figure 49.7: Ancient pyramids were probably constructed using ramps as simple machines. (credit: Franck Monnier, Wikimedia Commons) - (a) How long can you play tennis on the 800 kJ (about 200 kcal) of energy in a candy bar? (b) Does this seem like a long time? Discuss why exercise is necessary but may not be sufficient to cause a person to lose weight.
Footnotes
- 1 for an average 76-kg male
Glossary
- metabolic rate
- the rate at which the body uses food energy to sustain life and to do different activities
- basal metabolic rate
- the total energy conversion rate of a person at rest
- useful work
- work done on an external system
the rate at which the body uses food energy to sustain life and to do different activities
the total energy conversion rate of a person at rest
work done on an external system