Oscillatory Motion, Waves, and the Physics of Hearing

124 Waves

Learning Objectives

  • State the characteristics of a wave.
  • Calculate the velocity of wave propagation.
There is a high tidal wave of about 10 feet high in a sea. Three boats carrying three four persons each are ahead of the wave, which is coming toward them.
Figure 124.1: Waves in the ocean behave similarly to all other types of waves. (credit: Steve Jurveston, Flickr)

What is a wave? The most intuitive example is a water wave—a disturbance that propagates through a medium, moving from the place it was created. In water waves, this disturbance affects the water's surface, possibly caused by a splash or a falling object. In sound waves, the disturbance involves pressure variations in air. In earthquakes, disturbances travel through Earth's crust and interior. Even electromagnetic waves such as radio waves behave with similar principles. Across all types of waves, key characteristics like amplitude, frequency, and energy follow a unified set of physical rules. Waves that repeat regularly are associated with simple harmonic motion. Consider the stylized wave shown in Figure 124.2. It creates an up-and-down disturbance in the water, which causes a seagull to bob in harmonic motion as crests and troughs pass beneath it. The time for one full up-and-down motion is the wave's period [latex]T[/latex], and the frequency is given by:

[latex]f = \frac{1}{T}[/latex]

Although the disturbance moves to the right in the figure, the water itself does not move laterally—the gull remains in place vertically. This is because the energy moves, not the medium. The wave velocity [latex]v_{\text{w}}[/latex] describes the speed at which the disturbance propagates through the medium, and is sometimes called the propagation velocity.

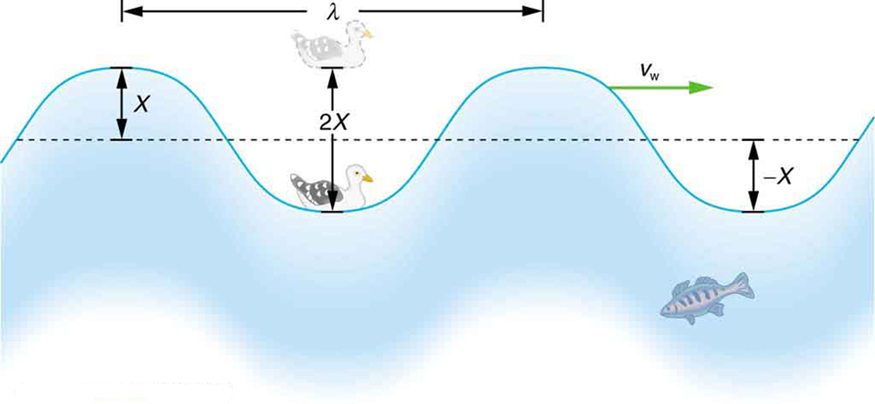
The figure shows an idealized ocean wave with two crests and two troughs that passes under a sea gull that bobs up and down in simple harmonic motion. The wave has a wavelength lambda which is the distance between adjacent identical parts of the wave. The height of a crest is equal to the depth of the trough that is X, therefore the total vertical distance between the top of a crest and the bottom of the trough is two-X.
Figure 124.2: An idealized ocean wave causes a sea gull to bob up and down. The wave has a wavelength [latex]\lambda[/latex], the distance between successive crests (or troughs), and propagates with speed [latex]v_{\text{w}}[/latex]. 

The wavelength [latex]\lambda[/latex] is the distance between two corresponding points on successive cycles of the wave—usually between adjacent crests or troughs. Since one full wavelength travels in the time of one period, the wave speed is given by:

[latex]v_{\text{w}} = \frac{\lambda}{T}[/latex]

Using the relationship [latex]f = \frac{1}{T}[/latex], we can also express wave speed as:

[latex]v_{\text{w}} = f \lambda[/latex]

This relationship holds for all waves: surface waves on water, sound waves in air, or light waves in a vacuum. The wave speed [latex]v_{\text{w}}[/latex] depends on the medium and type of wave.

Misconception Alert

Many people think waves transport the medium itself (like water in the ocean), but this is not true. The particles of the medium typically oscillate in place while the energy of the wave moves forward. So if you feel "pushed" by a wave in the ocean, you're feeling the force due to wave energy—not the bulk motion of water.

Take-Home Experiment: Waves in a Bowl

Fill a large bowl with water. Drop a cork gently into the center and observe the waves that form. Estimate the wavelength and period of the ripples. Try again by dropping the cork from a different height. Does the height of the drop affect the wavelength? What stays the same and what changes?

Example 124.1: Calculate the Velocity of Wave Propagation: Gull in the Ocean

Calculate the wave velocity of the ocean wave in Figure 124.2 if the distance between wave crests is 10.0 m and the time for a seagull to bob up and down is 5.00 s.

Strategy

We are asked to find [latex]{v}_{\text{w}}[/latex]. The given information tells us that [latex]\lambda =\text{10}\text{.}0\phantom{\rule{0.25em}{0ex}}\text{m}[/latex] and [latex]T=5\text{.}\text{00}\phantom{\rule{0.25em}{0ex}}\text{s}[/latex]. Therefore, we can use [latex]{v}_{\text{w}}=\frac{\lambda }{T}[/latex] to find the wave velocity.

Solution

  1. Enter the known values into [latex]{v}_{\text{w}}=\frac{\lambda }{T}[/latex]:
    [latex]{v}_{\text{w}}=\frac{\text{10.0 m}}{5\text{.00 s}}[/latex]
  2. Solve for [latex]{v}_{\text{w}}[/latex] to find [latex]{v}_{\text{w}}\text{= 2.00 m/s.}[/latex]

Discussion

This slow speed seems reasonable for an ocean wave. Note that the wave moves to the right in the figure at this speed, not the varying speed at which the seagull moves up and down.

Transverse and Longitudinal Waves

A wave is a periodic disturbance that travels through space or a medium. In a transverse wave, like the one shown in Figure 124.3, the disturbance occurs perpendicular to the direction the wave propagates. These are often called shear waves. In contrast, a longitudinal wave involves a disturbance that is parallel to the direction of propagation, as illustrated in Figure 124.4. The amplitude of a wave, represented as X, describes the size of the disturbance and is independent of the wave’s propagation speed [latex]{v}_{\text{w}}[/latex].

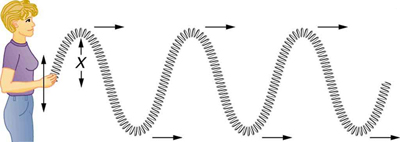
The figure shows a woman holding a long spring in her hand and moving it up and down causing it to move in a zigzag manner away from her. It is an example of a transverse wave, the wave propagates horizontally. The direction of motion of the wave is shown with the help of right arrows at each crest and trough.
Figure 124.3: In this transverse wave, the disturbance is vertical while the wave moves horizontally through the spring.
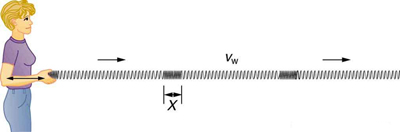
The figure shows a woman standing at left pushing a long spring in to and fro motion in horizontal direction away from her without moving her hand up and down. The cord stretches and contracts back and forth. This is an example of a longitudinal wave, the wave propagates horizontally. At some points the spring is compressed and at some other points the spring is expanded. One contracted part is equal to the amplitude X.
Figure 124.4: In this longitudinal wave, the disturbance and the direction of propagation are both horizontal.

Some waves combine both transverse and longitudinal components. For instance, water waves exhibit both types of motion. In the simplified model of a water wave shown in Figure 124.2, only the up-and-down (transverse) motion is visible, but real water waves involve circular particle motion due to both longitudinal and transverse effects. The type of wave depends on the medium. The vibrating strings of musical instruments produce transverse waves. Electromagnetic waves, such as visible light and radio waves, are also transverse. Sound waves in fluids (like air or water) are longitudinal, since fluids lack the structural rigidity required to support transverse shear waves. In solids, however, both longitudinal and transverse sound waves can exist.

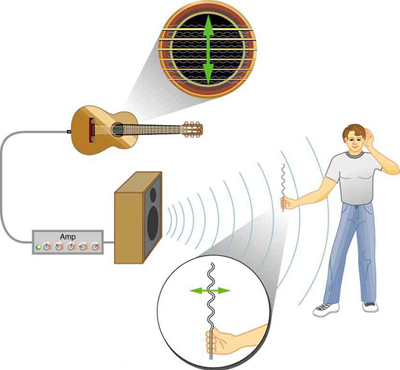
The figure shows a guitar connected to an amplifier and a man holding a sheet of paper facing the speaker attached to the amplifier. The strings of the guitar when played cause transverse waves. On the other hand, the sound of the guitar creates ripples on the sheet of paper causing it to rattle in a direction that shows that the sound waves are longitudinal.
Figure 124.5: The vibration of a guitar string produces transverse waves. The resulting sound wave is longitudinal, as demonstrated by the paper responding to compressions in air.

Seismic waves from earthquakes are another example. Beneath Earth’s surface, both longitudinal (P-waves) and transverse (S-waves) travel through rock. These wave types differ in speed and behavior. Earthquakes also produce surface waves similar to water waves, which can be particularly damaging.

Check Your Understanding

Why is it important to differentiate between longitudinal and transverse waves? Answer: Different wave types transfer energy differently through materials. Understanding whether the disturbance is parallel or perpendicular to the direction of motion helps us predict how energy will affect the surrounding medium.

Interactive Exploration: Wave on a String

Waves transfer energy from one location to another without transporting matter over long distances. In this simulation, you'll investigate how waves travel along a stretched string and how properties such as amplitude, frequency, tension, and damping influence their behavior. You'll also explore how waves reflect from different types of boundaries and how standing waves can be formed. Experiment by generating pulses or continuous waves while changing the frequency, amplitude, string tension, and damping. Try different boundary conditions, including fixed and loose ends, and observe how the waves propagate, reflect, and interfere. As you explore, relate these observations to the concepts developed in this chapter.

Guided Exploration

As you interact with the simulation, try to answer the following questions:

  1. Create a single pulse on the string. How does the pulse move, and what happens when it reaches the end of the string?
  2. Compare the reflections from a fixed end and a loose end. How are the reflected waves different?
  3. Increase the frequency while keeping the tension constant. How does this affect the wavelength of the wave?
  4. Increase the tension in the string. How does the wave speed change? What happens to the wavelength if the frequency remains constant?
  5. Introduce damping into the system. How does damping affect the amplitude and the energy carried by the wave?
  6. Generate a continuous wave and adjust the frequency until a standing wave forms. How many nodes and antinodes do you observe, and how do they change as you vary the frequency?

After completing the exploration, compare your observations with the concepts presented in this section. Notice that waves transport energy while the particles of the string simply oscillate about their equilibrium positions. Wave speed depends on the properties of the medium, while wavelength, frequency, and speed are related through the wave equation.

Healthcare Connection

Peristalsis, the wave-like motion that moves food through the digestive tract, is a genuine physiological wave. Rings of smooth muscle in the wall of the esophagus, stomach, and intestines contract and relax in a coordinated sequence, creating a traveling wave of muscular contraction that pushes the material inside forward, much as a wave travels along a rope even though each point on the rope only moves up and down. Disorders that disrupt this coordinated wave, such as certain motility disorders of the esophagus or intestine, can slow or block the movement of food and are diagnosed in part by measuring the speed, strength, and coordination of these contraction waves.

Section Summary

  • A wave is a disturbance that propagates through a medium with velocity [latex]{v}_{\text{w}}[/latex].
  • Wavelength [latex]\lambda[/latex] is the distance between successive identical parts of the wave.
  • The relationship between wave speed, frequency, and wavelength is [latex]{v}_{\text{w}}=\frac{\lambda}{T}[/latex] or [latex]{v}_{\text{w}}=f\lambda[/latex].
  • In transverse waves, the disturbance is perpendicular to wave propagation. In longitudinal waves, it is parallel.

Conceptual Questions

  1. Give one example of a transverse wave and another of a longitudinal wave, being careful to note the relative directions of the disturbance and wave propagation in each.
  2. What is the difference between propagation speed and the frequency of a wave? Does one or both affect wavelength? If so, how?

Problems & Exercises

  1. Storms in the South Pacific can create waves that travel all the way to the California coast, which are 12,000 km away. How long does it take them if they travel at 15.0 m/s?
  2. Waves on a swimming pool propagate at 0.750 m/s. You splash the water at one end of the pool and observe the wave go to the opposite end, reflect, and return in 30.0 s. How far away is the other end of the pool?
  3. Wind gusts create ripples on the ocean that have a wavelength of 5.00 cm and propagate at 2.00 m/s. What is their frequency?
  4. How many times a minute does a boat bob up and down on ocean waves that have a wavelength of 40.0 m and a propagation speed of 5.00 m/s?
  5. Scouts at a camp shake the rope bridge they have just crossed and observe the wave crests to be 8.00 m apart. If they shake the bridge twice per second, what is the propagation speed of the waves?
  6. What is the wavelength of the waves you create in a swimming pool if you splash your hand at a rate of 2.00 Hz and the waves propagate at 0.800 m/s?
  7. What is the wavelength of an earthquake that shakes you with a frequency of 10.0 Hz and gets to another city 84.0 km away in 12.0 s?
  8. Radio waves transmitted through space at [latex]3\text{.}\text{00}×{\text{10}}^{8}\phantom{\rule{0.25em}{0ex}}\text{m/s}[/latex] by the Voyager spacecraft have a wavelength of 0.120 m. What is their frequency?
  9. Your ear is capable of differentiating sounds that arrive at the ear just 1.00 ms apart. What is the minimum distance between two speakers that produce sounds that arrive at noticeably different times on a day when the speed of sound is 340 m/s?
  10. Answer the following questions:
    1. Seismographs measure the arrival times of earthquakes with a precision of 0.100 s. To get the distance to the epicenter of the quake, they compare the arrival times of S- and P-waves, which travel at different speeds. (See Figure 124.6.) If S- and P-waves travel at 4.00 and 7.20 km/s respectively, in the region considered, how precisely can the distance to the source of the earthquake be determined?
    2. Seismic waves from underground detonations of nuclear bombs can be used to locate the test site and detect violations of test bans. Discuss whether your answer to (a) implies a serious limit to such detection. (Note also that the uncertainty is greater if there is an uncertainty in the propagation speeds of the S- and P-waves.)
The figure shows a seismograph put on a wooden table. Its top is labeled as “Hands off glass, please”. Below it there are some buttons are shown and a paper roller is fitted in the seismograph to print the observation by the machine. On the right and left of the roller, two vertical cable slots are given.
Figure 124.6: A seismograph, as described in the above problem. (credit: Oleg Alexandrov)

Glossary

longitudinal wave
a wave in which the disturbance is parallel to the direction of propagation
transverse wave
a wave in which the disturbance is perpendicular to the direction of propagation
wave velocity
the speed at which the disturbance moves. Also called the propagation velocity or propagation speed
wavelength
the distance between adjacent identical parts of a wave
definition

License

Icon for the Creative Commons Attribution 4.0 International License

Introductory Physics for the Health and Life Sciences I Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book