"

Oscillatory Motion and Waves and Physics of Hearing.

121 Uniform Circular Motion and Simple Harmonic Motion

Learning Objectives

The figure shows a clock-wise rotating empty merry go round with iron bars holding the decorated wooden horse statues, four in each column.
Figure 121.1: The horses on this merry-go-round exhibit uniform circular motion. (credit: Wonderlane, Flickr)

You can produce simple harmonic motion (SHM) by projecting uniform circular motion. In Figure 121.2, a ball rotates on a vertical turntable and casts a shadow on the floor. That shadow moves back and forth in SHM.

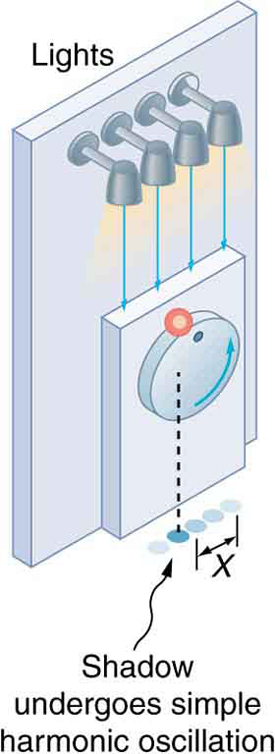
The given figure shows a vertical turntable with four floor projecting light bulbs at the top. A smaller sized rectangular bar is attached to this turntable at the bottom half, with a circular knob attached to it. A red colored small ball is rolling along the boundary of this knob in angular direction, and the lights falling through this ball are ball making shadows just under the knob on the floor. The middle shadow is the brightest and starts fading as we look through to the cornered shadow.
Figure 121.2: The shadow of a ball rotating at constant angular velocity [latex]\omega[/latex] undergoes simple harmonic motion.

Figure 121.3 illustrates how the projection of a point in uniform circular motion behaves like an object in SHM. A point [latex]P[/latex] moves around a circle with constant angular velocity [latex]\omega[/latex]. The horizontal projection of [latex]P[/latex] is position [latex]x[/latex], and its horizontal velocity is [latex]v[/latex], derived from the circular velocity [latex]{v}_{\text{max}}[/latex].

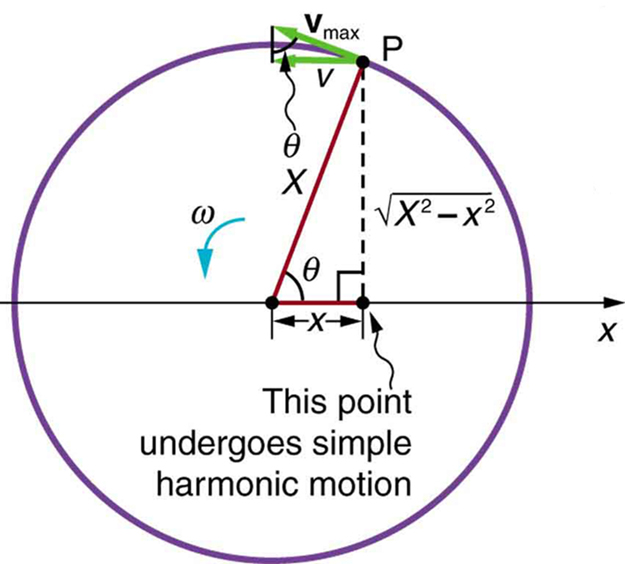
The figure shows a point P moving through the circumference of a circle in an angular way with angular velocity omega. The diameter is projected along the x axis, with point P making an angle theta at the centre of the circle. A point along the diameter shows the projection of the point P with a dotted perpendicular line from P to this point, the projection of the point is given as v along the circle and its velocity v subscript max, over the top of the projection arrow in an upward left direction.
Figure 121.3: Point [latex]P[/latex] undergoes circular motion, and its horizontal projection executes simple harmonic motion. The velocity vector [latex]v[/latex] and its projection correspond to the SHM velocity.

The position of the shadow or projection is given by:

[latex]x = X \cos(\theta)[/latex]

Since [latex]\theta = \omega t[/latex], we can write:

[latex]x = X \cos(\omega t)[/latex]

Substituting [latex]\omega = \frac{2\pi}{T}[/latex] gives:

[latex]x(t) = X \cos\left(\frac{2\pi t}{T}\right)[/latex]

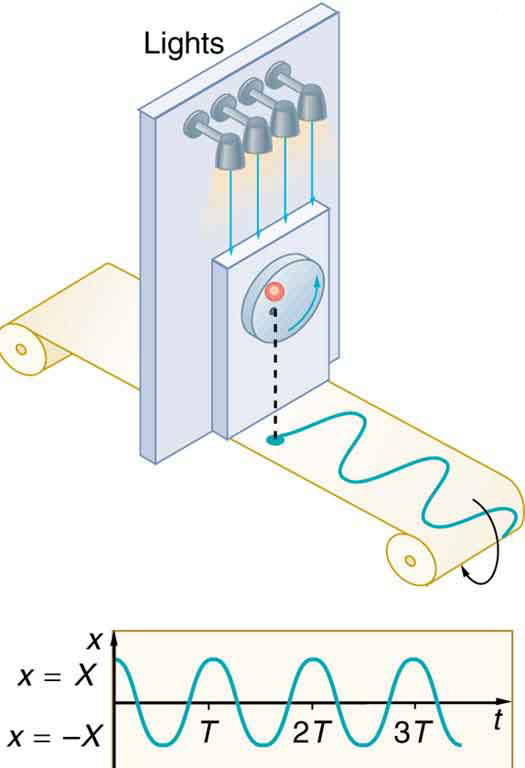
This is the same position function for SHM derived earlier in the study of oscillations. The wavelike character of the motion is evident in Figure 121.4.

The given figure shows a vertical turntable with four floor projecting light bulbs at the top. A smaller sized rectangular bar is attached to this turntable at the bottom half, with a circular knob attached to it. A red colored small ball is rolling along the boundary of this knob in angular direction. The turnaround table is put upon a roller paper sheet, on which the simple harmonic motion is measured, which is shown here in oscillating waves on the paper sheet in front of the table. A graph of amplitude versus time is also given alongside the figure.
Figure 121.4: The projection of uniform circular motion creates a wave representing SHM in position versus time.

Mathematical Relationship

From Figure 121.3, velocity [latex]v[/latex] at position [latex]x[/latex] is:

[latex]v = {v}_{\text{max}} \sqrt{1 - \frac{x^2}{X^2}}[/latex]

This matches the velocity derived from conservation of energy in SHM. The period of the circular motion is the time to complete one revolution, or:

[latex]T = \frac{2\pi X}{{v}_{\text{max}}}[/latex]

Using [latex]{v}_{\text{max}} = \sqrt{\frac{k}{m}} X[/latex], we substitute:

[latex]\frac{X}{{v}_{\text{max}}} = \sqrt{\frac{m}{k}}[/latex]

Which gives us:

[latex]T = 2\pi \sqrt{\frac{m}{k}}[/latex]

This is the period of a simple harmonic oscillator, confirming the equivalence.

Check Your Understanding

Identify an object that undergoes uniform circular motion. Describe how you could trace its simple harmonic motion as a wave.
A record player undergoes uniform circular motion. You could attach a dowel to the outer edge of the turntable with a pen on the end. As it spins, drag a long strip of paper underneath the pen to trace the SHM as a wave.

Section Summary

  • The projection of an object in uniform circular motion follows simple harmonic motion.
  • The mathematical descriptions for SHM can be derived from the geometry of circular motion.
  • The relationship helps explain physical waveforms, resonance, and systems such as pendulums and springs.

Problems & Exercises

  1. (a)What is the maximum velocity of an 85.0-kg person bouncing on a bathroom scale having a force constant of [latex]1\text{.}\text{50}×{\text{10}}^{6}\phantom{\rule{0.25em}{0ex}}\text{N/m}[/latex], if the amplitude of the bounce is 0.200 cm? (b)What is the maximum energy stored in the spring?
  2. A novelty clock has a 0.0100-kg mass object bouncing on a spring that has a force constant of 1.25 N/m. What is the maximum velocity of the object if the object bounces 3.00 cm above and below its equilibrium position? (b) How many joules of kinetic energy does the object have at its maximum velocity?
  3. At what positions is the speed of a simple harmonic oscillator half its maximum? That is, what values of [latex]x/X[/latex] give [latex]v=±{v}_{\text{max}}/2[/latex], where [latex]X[/latex] is the amplitude of the motion?
  4. A ladybug sits 12.0 cm from the center of a Beatles music album spinning at 33.33 rpm. What is the maximum velocity of its shadow on the wall behind the turntable, if illuminated parallel to the record by the parallel rays of the setting Sun?
definition

License

Icon for the Creative Commons Attribution 4.0 International License

Introductory Physics for the Health and Life Sciences I Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book