"

Kinematics

10 Time, Velocity, and Speed

Learning Objectives

  • Explain the relationships between instantaneous velocity, average velocity, instantaneous speed, average speed, displacement, and time.
  • Calculate velocity and speed given initial position, initial time, final position, and final time.
  • Derive a graph of velocity vs. time given a graph of position vs. time.
  • Interpret a graph of velocity vs. time.

 

Snails leaving slime trails as they race each other along a flat surface.
Figure 9.1: The motion of these racing snails can be described using concepts of speed and velocity. While speed refers to how fast the snails move, velocity also includes the direction of their motion. (credit: tobitasflickr, Flickr)

Time

As discussed in Physical Quantities and Units, time is one of the most fundamental quantities in physics. It allows us to quantify change—whether it’s a pulse, a moving cell under a microscope, or the rotation of the Earth.

In physics, elapsed time tells us how much time has passed between two events. It is calculated as

[latex]\Delta t = t_f - t_0[/latex]

Where [latex]\Delta t[/latex] is the elapsed time, [latex]t_0[/latex] the starting time and [latex]t_f[/latex] the final time.

We often simplify problems by setting [latex]t_0=0[/latex],  in which case [latex]\Delta t=t[/latex]

Average Velocity

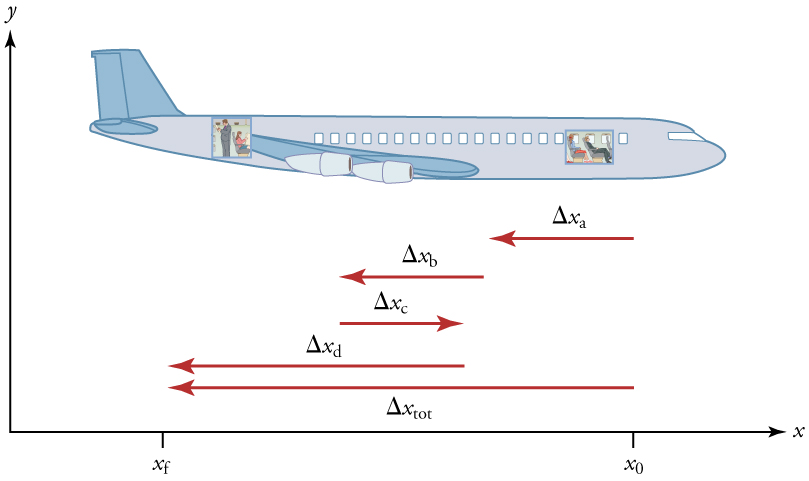
Velocity is defined as displacement divided by time. It is a vector, meaning it includes both magnitude and direction.

[latex]\bar{v} = \frac{\Delta x}{\Delta t} = \frac{x_f - x_0}{t_f - t_0}[/latex]

If the object moves −4.0 m in 5.0 s (toward the rear), the average velocity is:

[latex]\bar{v} = \frac{-4.0m}{5.0s} = -0.8m/s[/latex]

The negative sign shows the direction is opposite to the chosen positive direction.

Airplane shown from the outside. Vector arrows show paths of each individual segment of the passenger’s trip to the back of the plane.
Figure 9.2: A more detailed view of a passenger walking toward the back of the plane. By examining smaller segments of motion, we gain a clearer understanding of how velocity changes over time.

Instantaneous Velocity

While average velocity tells us about displacement over a longer time, instantaneous velocity tells us how fast something is moving at an exact moment—like a speedometer reading.

In biological experiments, instantaneous velocity helps describe fast processes like blood flow through vessels or chemical diffusion rates.

Speed vs Velocity

  • Speed is a scalar—it has magnitude only (no direction).

  • Velocity is a vector—it includes both magnitude and direction.

Even if velocity is negative (e.g., −3.0 m/s), the speed is simply the absolute value: 3.0 m/s.

[latex]\text{Average speed} = \frac{\text{Distance}}{\text{Elapsed time}}[/latex]

Unlike velocity, average speed doesn’t care about direction. It is based on distance traveled, not displacement.

A house and a store, with a set of arrows in between showing that the distance between them is 3 point 0 kilometers and the total distance traveled, delta x total, equals 0 kilometers.
Figure 9.3: On a 30-minute round trip to a store, the total distance traveled is 6 km. The average speed is 12 km/h, but the average velocity is zero—because the person returns to the starting point, resulting in zero displacement.

Graphical View of Motion

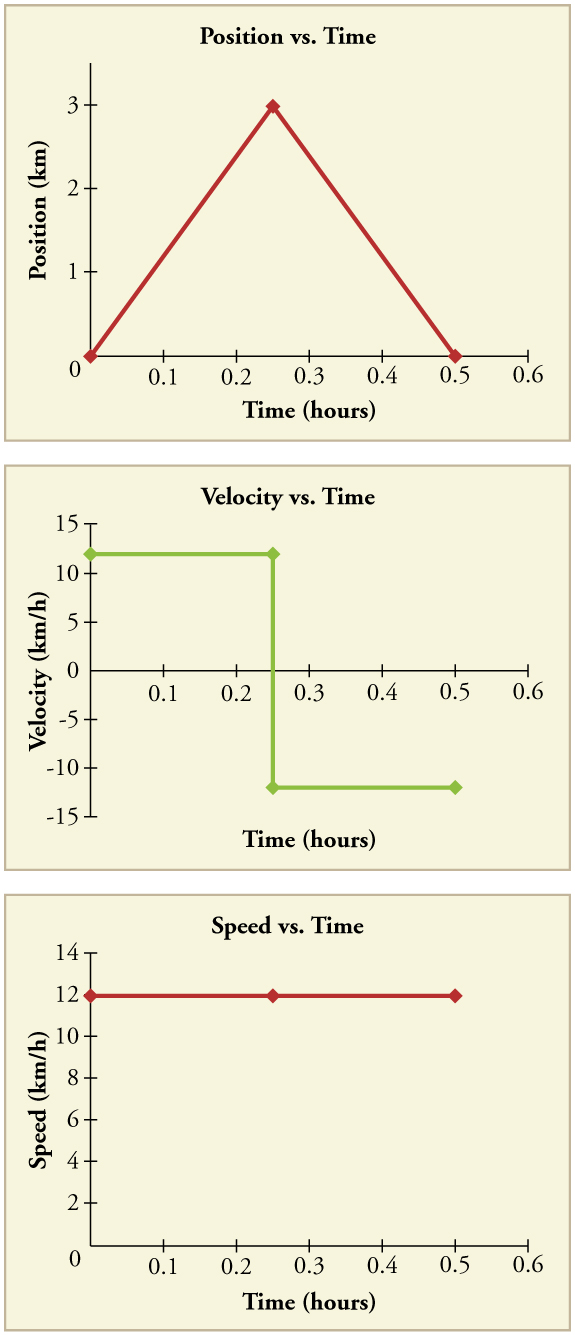
Position-time, velocity-time, and speed-time graphs provide visual ways to understand motion. While real-life motion is often irregular, we simplify it in models to make key ideas clear. An example is shown in Figure 9.4.

Three line graphs. First line graph is of position in kilometers versus time in hours. The line increases linearly from 0 kilometers to 6 kilometers in the first 0 point 25 hours. It then decreases linearly from 6 kilometers to 0 kilometers between 0 point 25 and 0 point 5 hours. Second line graph shows velocity in kilometers per hour versus time in hours. The line is flat at 12 kilometers per hour from time 0 to time 0 point 25. It is vertical at time 0 point 25, dropping from 12 kilometers per hour to negative 12 kilometers per hour. It is flat again at negative 12 kilometers per hour from 0 point 25 hours to 0 point 5 hours. Third line graph shows speed in kilometers per hour versus time in hours. The line is flat at 12 kilometers per hour from time equals 0 to time equals 0 point 5 hours.
Figure 9.4: Graphs showing position, velocity, and speed versus time during a simplified trip. Note that velocity is negative on the return trip, but speed remains positive.

Making Connections: Take-Home Investigation—Getting a Sense of Speed

To build intuition about motion in real-world terms:

  • Time yourself walking or jogging 10 meters, then calculate your speed in m/s and convert to km/h or mi/h.

  • Estimate how fast a leaf falls or an insect moves.

  • Convert 10, 20, and 60 mi/h into m/s—what does that feel like?

Check Your Understanding

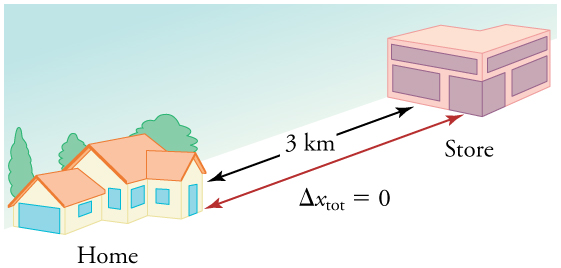
A commuter train travels from Baltimore to Washington, D.C., and returns in 1 hour 45 minutes (105 min). The one-way distance is 40 miles.

(a) What is the average velocity?

  • The displacement is zero because the train ends at its starting location.

  • So, average velocity = 0 m/s

(b) What is the average speed?

[latex]\text{Average speed} = \frac{80\ \text{miles}}{105\ \text{min}} \approx 20\ \text{m/s}[/latex]

(using unit conversions: miles → meters, minutes → seconds)

Section Summary

  • Time measures change; its SI unit is the second (s).

  • Elapsed time:

[latex]\Delta t = t_f - t_0[/latex]​

  • Velocity: a vector defined by displacement over time:

[latex]\text{Average speed} = \frac{\text{Distance}}{\text{Elapsed time}}[/latex]

  • Speed: a scalar defined by distance over time:

  • Instantaneous velocity describes motion at a specific moment.

  • Average speed can be greater than the magnitude of average velocity.

  • Graphs (position-time, velocity-time) help visualize and compare motion.

Conceptual Questions

  1. Give an example (but not one from the text) of a device used to measure time and identify what change in that device indicates a change in time.
  2. There is a distinction between average speed and the magnitude of average velocity. Give an example that illustrates the difference between these two quantities
  3. Does a car’s odometer measure position or displacement? Does its speedometer measure speed or velocity?
  4. If you divide the total distance traveled on a car trip (as determined by the odometer) by the time for the trip, are you calculating the average speed or the magnitude of the average velocity? Under what circumstances are these two quantities the same?
  5. How are instantaneous velocity and instantaneous speed related to one another? How do they differ?

Problems & Exercises

  1. Answer the following questions
    1. Calculate Earth’s average speed relative to the Sun.
    2. What is its average velocity over a period of one year?
  2. A helicopter blade spins at exactly 100 revolutions per minute. Its tip is 5.00 m from the center of rotation.
    1. Calculate the average speed of the blade tip in the helicopter’s frame of reference.
    2. What is its average velocity over one revolution?
  3. The North American and European continents are moving apart at a rate of about 3 cm/y. At this rate how long will it take them to drift 500 km farther apart than they are at present?
  4. Land west of the San Andreas fault in southern California is moving at an average velocity of about 6 cm/y northwest relative to land east of the fault. Los Angeles is west of the fault and may thus someday be at the same latitude as San Francisco, which is east of the fault. How far in the future will this occur if the displacement to be made is 590 km northwest, assuming the motion remains constant?
  5. On May 26, 1934, a streamlined, stainless steel diesel train called the Zephyr set the world’s nonstop long-distance speed record for trains. Its run from Denver to Chicago took 13 hours, 4 minutes, 58 seconds, and was witnessed by more than a million people along the route. The total distance traveled was 1633.8 km. What was its average speed in km/h and m/s?
  6. Tidal friction is slowing the rotation of the Earth. As a result, the orbit of the Moon is increasing in radius at a rate of approximately 4 cm/year. Assuming this to be a constant rate, how many years will pass before the radius of the Moon’s orbit increases by [latex]3\text{.}\text{84}×{\text{10}}^{6}\phantom{\rule{0.25em}{0ex}}m[/latex] (1%)?
  7. A student drove to the university from her home and noted that the odometer reading of her car increased by 12.0 km. The trip took 18.0 min
    1. What was her average speed?
    2. If the straight-line distance from her home to the university is 10.3 km in a direction [latex]\text{25}\text{.}0º[/latex] south of east, what was her average velocity?
    3. If she returned home by the same path 7 h 30 min after she left, what were her average speed and velocity for the entire trip?
  8. The speed of propagation of the action potential (an electrical signal) in a nerve cell depends (inversely) on the diameter of the axon (nerve fiber). If the nerve cell connecting the spinal cord to your feet is 1.1 m long, and the nerve impulse speed is 18 m/s, how long does it take for the nerve signal to travel this distance?
  9. Conversations with astronauts on the lunar surface were characterized by a kind of echo in which the earthbound person’s voice was so loud in the astronaut’s space helmet that it was picked up by the astronaut’s microphone and transmitted back to Earth. It is reasonable to assume that the echo time equals the time necessary for the radio wave to travel from the Earth to the Moon and back (that is, neglecting any time delays in the electronic equipment). Calculate the distance from Earth to the Moon given that the echo time was 2.56 s and that radio waves travel at the speed of light [latex]\left(3\text{.}\text{00}×{\text{10}}^{8}\phantom{\rule{0.25em}{0ex}}\text{m/s}\right)[/latex].
  10. A football quarterback runs 15.0 m straight down the playing field in 2.50 s. He is then hit and pushed 3.00 m straight backward in 1.75 s. He breaks the tackle and runs straight forward another 21.0 m in 5.20 s. Calculate his average velocity:
    1. for each of the three intervals and
    2. for the entire motion.
  11. The planetary model of the atom pictures electrons orbiting the atomic nucleus much as planets orbit the Sun. In this model you can view hydrogen, the simplest atom, as having a single electron in a circular orbit [latex]1\text{.}\text{06}×{\text{10}}^{-\text{10}}\phantom{\rule{0.25em}{0ex}}\text{m}[/latex] in diameter.
    1. If the average speed of the electron in this orbit is known to be [latex]2\text{.}\text{20}×{\text{10}}^{6}\phantom{\rule{0.25em}{0ex}}\text{m/s}[/latex], calculate the number of revolutions per second it makes about the nucleus.
    2. What is the electron’s average velocity?

Glossary

average speed
distance traveled divided by time during which motion occurs
average velocity
displacement divided by time over which displacement occurs
instantaneous velocity
velocity at a specific instant, or the average velocity over an infinitesimal time interval
instantaneous speed
magnitude of the instantaneous velocity
time
change, or the interval over which change occurs
model
simplified description that contains only those elements necessary to describe the physics of a physical situation
elapsed time
the difference between the ending time and beginning time
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book