"

Temperature, Kinetic Theory, and the Gas Laws

94 Thermal Expansion of Solids and Liquids

Thermal Expansion

Learning Objectives

  • Define and describe the phenomenon of thermal expansion.
  • Calculate linear expansion using initial length, temperature change, and the coefficient of linear expansion.
  • Calculate volume expansion using initial volume, temperature change, and the coefficient of volume expansion.
  • Calculate thermal stress from volume change, temperature change, and bulk modulus.
Figure 94.1: Thermal expansion joints like these in the Auckland Harbour Bridge in New Zealand allow bridges to change length without buckling. (credit: Ingolfson, Wikimedia Commons)

Many materials expand or contract with changes in temperature. This effect, called thermal expansion, is evident in everyday life. One common example is the expansion of the colored alcohol in a thermometer. On a larger scale, bridges such as the Auckland Harbour Bridge in New Zealand are constructed with thermal expansion joints to allow structural components to lengthen or shorten with temperature changes without causing damage (see Figure 94.1).

In fluids, thermal expansion causes warm air to rise: the increased temperature lowers the air’s density, which leads to buoyant upward motion. This effect drives natural convection in homes, atmospheric currents, and even circulation in oceans. In the human body, thermal expansion contributes to blood vessel dilation in response to heat.

Thermal expansion is influenced by two main factors:

  1. It is proportional to the temperature change—greater temperature changes produce greater expansion.
  2. It depends on the material—different substances expand at different rates. For example, alcohol expands much more than glass, which is why it rises visibly in thermometers.

Thermal expansion originates from the increased kinetic energy of atoms or molecules as temperature rises. In a solid, atoms vibrate more rapidly as they gain energy. These vibrations cause atoms to push against neighboring atoms, increasing the average spacing and leading to a net increase in the object’s size. Since most solids have no preferred direction for these motions, the expansion is usually uniform in all dimensions.

Linear Thermal Expansion

For practical calculations, we often consider expansion in one dimension—for instance, the elongation of a metal rod. The change in length [latex]\Delta L[/latex] due to a temperature change [latex]\Delta T[/latex] is given by:

[latex]\Delta L = \alpha L \Delta T[/latex]

Here, [latex]L[/latex] is the original length and [latex]\alpha[/latex] is the coefficient of linear expansion. The coefficient [latex]\alpha[/latex] varies depending on the material and is typically given in units of [latex](1/\text{ºC})[/latex] or [latex](1/\text{K})[/latex]. Since the size of one kelvin is the same as one degree Celsius, [latex]\Delta T[/latex] can be in either unit.

This equation is accurate for small temperature changes. For larger changes, using an average value of [latex]\alpha[/latex] provides reasonable accuracy.

Thermal Expansion Coefficients

The coefficients of linear and volume expansion vary widely between materials. Table 94.2 lists representative values for common solids, liquids, and gases at [latex]20^\circ \text{C}[/latex]. These values help engineers, architects, and medical scientists account for expansion when designing equipment, structures, or biological models.

Table 94.2: Thermal Expansion Coefficients at [latex]\text{20}\text{º}\text{C}[/latex]1
Material Coefficient of linear expansion [latex]\alpha \left(1/\text{º}\text{C}\right)[/latex] Coefficient of volume expansion [latex]\beta \left(1/\text{º}\text{C}\right)[/latex]
Solids
Aluminum [latex]\text{25}×{\text{10}}^{–6}[/latex] [latex]\text{75}×{\text{10}}^{–6}[/latex]
Brass [latex]\text{19}×{\text{10}}^{–6}[/latex] [latex]\text{56}×{\text{10}}^{–6}[/latex]
Copper [latex]\text{17}×{\text{10}}^{–6}[/latex] [latex]\text{51}×{\text{10}}^{–6}[/latex]
Gold [latex]\text{14}×{\text{10}}^{–6}[/latex] [latex]\text{42}×{\text{10}}^{–6}[/latex]
Iron or Steel [latex]\text{12}×{\text{10}}^{–6}[/latex] [latex]\text{35}×{\text{10}}^{–6}[/latex]
Invar (Nickel-iron alloy) [latex]0\text{.}9×{\text{10}}^{–6}[/latex] [latex]2\text{.}7×{\text{10}}^{–6}[/latex]
Lead [latex]\text{29}×{\text{10}}^{–6}[/latex] [latex]\text{87}×{\text{10}}^{–6}[/latex]
Silver [latex]\text{18}×{\text{10}}^{–6}[/latex] [latex]\text{54}×{\text{10}}^{–6}[/latex]
Glass (ordinary) [latex]9×{\text{10}}^{–6}[/latex] [latex]\text{27}×{\text{10}}^{–6}[/latex]
Glass (Pyrex®) [latex]3×{\text{10}}^{–6}[/latex] [latex]9×{\text{10}}^{–6}[/latex]
Quartz [latex]0\text{.}4×{\text{10}}^{–6}[/latex] [latex]1×{\text{10}}^{–6}[/latex]
Concrete, Brick [latex]\text{~}\text{12}×{\text{10}}^{–6}[/latex] [latex]\text{~}\text{36}×{\text{10}}^{–6}[/latex]
Marble (average) [latex]7×{\text{10}}^{–6}[/latex] [latex]2\text{.}1×{\text{10}}^{–5}[/latex]
Liquids
Ether [latex]\text{1650}×{\text{10}}^{–6}[/latex]
Ethyl alcohol [latex]\text{1100}×{\text{10}}^{–6}[/latex]
Petrol [latex]\text{950}×{\text{10}}^{–6}[/latex]
Glycerin [latex]\text{500}×{\text{10}}^{–6}[/latex]
Mercury [latex]\text{180}×{\text{10}}^{–6}[/latex]
Water [latex]\text{210}×{\text{10}}^{–6}[/latex]
Gases
Air and most other gases at atmospheric pressure [latex]\text{3400}×{\text{10}}^{–6}[/latex]

Calculating Linear Thermal Expansion: The Golden Gate Bridge

The main span of San Francisco’s Golden Gate Bridge is 1275 m long at its coldest. The bridge is exposed to temperatures ranging from [latex]–\text{15}\text{º}\text{C}[/latex] to [latex]\text{40}\text{º}\text{C}[/latex]. What is its change in length between these temperatures? Assume that the bridge is made entirely of steel.

Strategy

Use the equation for linear thermal expansion [latex]\text{Δ}L=\mathrm{\alpha L}\text{Δ}T[/latex] to calculate the change in length , [latex]\text{Δ}L[/latex]. Use the coefficient of linear expansion, [latex]\alpha[/latex], for steel from Table 94.2, and note that the change in temperature, [latex]\text{Δ}T[/latex], is [latex]\text{55}\text{º}\text{C}[/latex].

Solution

Plug all of the known values into the equation to solve for [latex]\text{Δ}L[/latex].

[latex]\text{Δ}L=\mathrm{\alpha L}\text{Δ}T=\left(\frac{\text{12}×{\text{10}}^{-6}}{\text{º}\text{C}}\right)\left(\text{1275 m}\right)\left(\text{55}\text{º}\text{C}\right)=0\text{.}\text{84 m.}[/latex]

Discussion

Although not large compared with the length of the bridge, this change in length is observable. It is generally spread over many expansion joints so that the expansion at each joint is small.

Thermal Expansion in Two and Three Dimensions

While we often describe thermal expansion in terms of length, real-world objects expand in all directions when heated. This means that both the area and volume of an object increase with temperature, not just its length. Even holes expand with heating—a counterintuitive result. If you cut a circular hole in a metal sheet, the hole expands with the surrounding material. As shown in Figure 94.2, the atoms or molecules at the edge of the hole move farther apart as they vibrate more energetically due to the temperature increase. This effectively causes the hole itself to enlarge.

Thermal Expansion in Two Dimensions

When temperature changes are relatively small, the change in area [latex]\Delta A[/latex] of a flat object is given by the equation:

[latex]\Delta A = 2 \alpha A \Delta T[/latex]

Here, [latex]A[/latex] is the original area, [latex]\Delta T[/latex] is the temperature change, and [latex]\alpha[/latex] is the coefficient of linear expansion. This formula arises because both length and width increase proportionally to temperature, doubling the expansion effect in two dimensions.

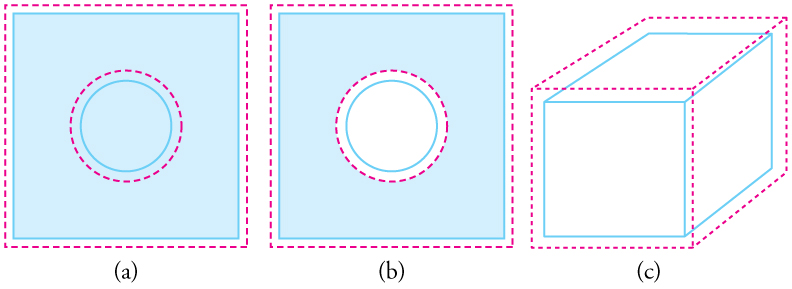
Part a shows the outline of a flat metal plate before and after expansion. After expansion, it has the same shape and ratio of dimensions as before, but it takes up a greater area. Part b shows the outline of a flat metal plate with a hole in it, before and after expansion. The hole expands. Part c shows the outline of a rectangular box before and after expansion. After expansion, the box has the same proportions as before expansion, but it has a greater volume.
Figure 94.2: Objects expand in all directions with temperature. (a) A flat metal plate expands in both length and width. (b) A hole in the plate expands just like the surrounding metal. (c) A box expands in all three dimensions. Dashed lines represent expanded boundaries. Adapted from OpenStax.

Thermal Expansion in Three Dimensions

For volumetric expansion, the change in volume [latex]\Delta V[/latex] is given by:

[latex]\Delta V = \beta V \Delta T[/latex]

Here, [latex]V[/latex] is the original volume and [latex]\beta[/latex] is the coefficient of volume expansion, which is approximately three times the linear coefficient: [latex]\beta \approx 3\alpha[/latex]. This relationship reflects expansion along three perpendicular axes.

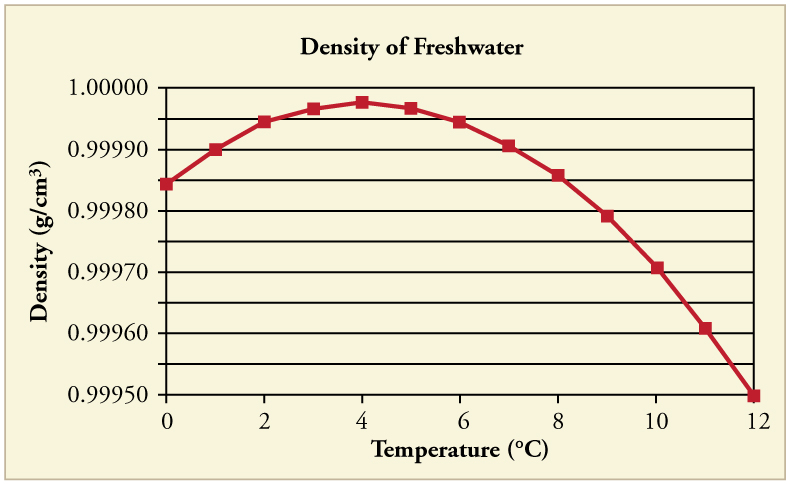
Most substances expand uniformly with increasing temperature. However, water is a unique exception. As shown in Figure 94.3, water is densest at [latex]4^\circ\text{C}[/latex]. Below this temperature, water actually expands as it cools, which is why ice floats. This anomalous behavior of water has vital ecological consequences. During winter, the surface of a lake can freeze, forming a layer of ice that insulates the liquid water below. Aquatic organisms survive the cold months in this thermally protected layer, maintaining life in freshwater ecosystems.

A graph of density of freshwater in grams per cubic centimeter versus temperature in degrees Celsius. The line is convex up. At zero degrees C, the density is just under zero point nine nine nine five grams per cubic centimeter. The density then increases at a decreasing rate until it hits a peak of about zero point nine nine nine nine seven grams per cubic centimeter at about four degrees C. Above four degrees C, the density decreases with increasing temperature.
Figure 94.3: Water reaches maximum density at [latex]4^\circ\text{C}[/latex]. This unusual thermal expansion behavior enables aquatic life to survive below frozen lake surfaces. Adapted from OpenStax.

Making Connections: Fuel Tanks and Thermal Expansion

Thermal expansion affects many practical situations. One example is what happens when you fill your gas tank on a hot summer day. Gasoline stored underground is cooler than the surrounding air. When it’s pumped into your car’s tank, the metal tank and the fuel both warm up, but the gasoline expands more than the steel tank. This can lead to overflow shortly after refueling.

Even the gas gauge reading can be misleading. Because the tank’s volume is constant while the gasoline’s volume changes with temperature, a tank that appears “full” in summer may contain less mass (and thus less energy) than in winter. So if you typically drive 40 miles after the “empty” light turns on in winter, don’t expect the same in July—you might run out sooner!

Fuel gauge pointing to empty.
Figure 94.4: Because gasoline expands more than the tank itself, you may have less fuel by mass in summer than winter, even when the volume appears full. Adapted from OpenStax.

Example 94.2: Calculating Thermal Expansion: Gas vs. Gas Tank

Suppose your 60.0-L (15.9-gal) steel gasoline tank is full of gas, so both the tank and the gasoline have a temperature of [latex]\text{15}\text{.}0\text{º}\text{C}[/latex]. How much gasoline has spilled by the time they warm to [latex]\text{35}\text{.}0\text{º}\text{C}[/latex]?

Strategy

The tank and gasoline increase in volume, but the gasoline increases more, so the amount spilled is the difference in their volume changes. (The gasoline tank can be treated as solid steel.) We can use the equation for volume expansion to calculate the change in volume of the gasoline and of the tank.

Solution

  1. Use the equation for volume expansion to calculate the increase in volume of the steel tank:
    [latex]{\text{Δ}V}_{\text{s}}={\beta }_{\text{s}}{V}_{\text{s}}\text{Δ}T.[/latex]
  2. The increase in volume of the gasoline is given by this equation:
    [latex]{\text{Δ}V}_{\text{gas}}={\beta }_{\text{gas}}{V}_{\text{gas}}\text{Δ}T.[/latex]
  3. Find the difference in volume to determine the amount spilled as
    [latex]{V}_{\text{spill}}={\text{Δ}V}_{\text{gas}}-{\text{Δ}V}_{\text{s}}.[/latex]

    Alternatively, we can combine these three equations into a single equation. (Note that the original volumes are equal.)

    [latex]\begin{array}{lll}{V}_{\text{spill}}& =& \left({\beta }_{\text{gas}}-{\beta }_{\text{s}}\right)V\text{Δ}T\\ & =& \left[\left(\text{950}-\text{35}\right)×{\text{10}}^{-6}/\text{º}\text{C}\right]\left(\text{60}\text{.}0\phantom{\rule{0.25em}{0ex}}\text{L}\right)\left(\text{20}\text{.}0\text{º}\text{C}\right)\\ & =& 1\text{.}\text{10}\phantom{\rule{0.25em}{0ex}}\text{L}.\end{array}[/latex]

Discussion

This amount is significant, particularly for a 60.0-L tank. The effect is so striking because the gasoline and steel expand quickly. The rate of change in thermal properties is discussed in Heat and Heat Transfer Methods.

If you try to cap the tank tightly to prevent overflow, you will find that it leaks anyway, either around the cap or by bursting the tank. Tightly constricting the expanding gas is equivalent to compressing it, and both liquids and solids resist being compressed with extremely large forces. To avoid rupturing rigid containers, these containers have air gaps, which allow them to expand and contract without stressing them.

Thermal Stress

When materials expand or contract due to temperature changes and are restrained from doing so freely, they develop internal forces. These forces are known as thermal stress. Thermal stress is a direct consequence of thermal expansion in constrained environments. For a deeper discussion of internal forces in materials, see the chapter on Elasticity: Stress and Strain.

Thermal stress can have destructive consequences. For example, if gasoline expands inside a sealed metal tank on a hot day, the resulting pressure can rupture the container. Similarly, roads and sidewalks crack over time due to repeated expansion and contraction with temperature cycles. In cold climates, water that seeps into pavement or rocks expands when it freezes, causing further cracking and fragmentation.

Yet thermal stress is also harnessed in manufacturing. One common practice is to heat a metal ring, expand it thermally, and slip it over another part. As the ring cools, it contracts and forms a tight mechanical fit. This technique is used in applications like attaching wheels to axles or joining parts in engines and turbines.

In biological systems, temperature changes can also induce stress in tissues, prosthetics, or implants if different materials expand at different rates. Understanding thermal stress is therefore relevant in medical device design and materials engineering for biomedical applications.

Example 94.3: Calculating Thermal Stress: Gas Pressure

What pressure would be created in the gasoline tank considered in Example 94.2, if the gasoline increases in temperature from [latex]\text{15}\text{.}0\text{º}\text{C}[/latex] to [latex]\text{35}\text{.}0\text{º}\text{C}[/latex] without being allowed to expand? Assume that the bulk modulus [latex]B[/latex] for gasoline is [latex]1\text{.}\text{00}×{\text{10}}^{9}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}[/latex]. (For more on bulk modulus, see Elasticity: Stress and Strain.)

Strategy

To solve this problem, we must use the following equation, which relates a change in volume [latex]\text{Δ}V[/latex] to pressure:

[latex]\text{Δ}V=\frac{1}{B}\frac{F}{A}{V}_{0},[/latex]

where [latex]F/A[/latex] is pressure, [latex]{V}_{0}[/latex] is the original volume, and [latex]B[/latex] is the bulk modulus of the material involved. We will use the amount spilled in Example 94.2 as the change in volume, [latex]\text{Δ}V[/latex].

Solution

  1. Rearrange the equation for calculating pressure:
    [latex]P=\frac{F}{A}=\frac{\text{Δ}V}{{V}_{0}}B\text{.}[/latex]
  2. Insert the known values. The bulk modulus for gasoline is [latex]B=1\text{.}\text{00}×{\text{10}}^{9}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}[/latex]. In the previous example, the change in volume [latex]\text{Δ}V=1\text{.}\text{10}\phantom{\rule{0.25em}{0ex}}\text{L}[/latex] is the amount that would spill. Here, [latex]{V}_{0}=\text{60}\text{.}0\phantom{\rule{0.25em}{0ex}}\text{L}[/latex] is the original volume of the gasoline. Substituting these values into the equation, we obtain
    [latex]P=\frac{1\text{.}\text{10 L}}{\text{60}\text{.}\text{0 L}}\left(1\text{.}\text{00}×{\text{10}}^{9}\phantom{\rule{0.25em}{0ex}}\text{Pa}\right)=1\text{.}\text{83}×{\text{10}}^{7}\phantom{\rule{0.25em}{0ex}}\text{Pa}\text{.}[/latex]

Discussion

This pressure is about [latex]\text{2500}\phantom{\rule{0.25em}{0ex}}{\text{lb/in}}^{2}[/latex], much more than a gasoline tank can handle.

Thermal Stress and Its Effects

When materials expand or contract due to changes in temperature but are constrained from freely doing so, they experience thermal stress. This internal stress can generate forces large enough to damage structures or devices. Common examples include the buckling of railroad tracks and roads on hot days if proper expansion joints are not in place. (Figure 94.5).

In colder conditions, a lack of slack in structures such as electrical wires can lead to snapping due to contraction. Similarly, cracks in plaster walls open and close with seasonal temperature changes. Even common glass cookware can fracture when cooled rapidly, as uneven contraction generates stress across the surface. This is why materials like Pyrex®—which have very low coefficients of thermal expansion—are preferred for high-temperature use.

Rapid temperature changes can also be dangerous in industrial settings. For example, the pressure vessels in nuclear reactors must be cooled gradually. If cooled too quickly, large temperature gradients can create significant thermal stresses. Although no failures have occurred, some reactors have experienced cooling rates faster than considered safe.

Thermal stress in biological and ecological systems is also important. During food freezing, biological cells rupture due to the expansion of water upon freezing, which compromises texture and taste. Repeated freeze-thaw cycles worsen the damage, a problem relevant in both food preservation and cryobiology. At a global scale, the thermal expansion of ocean water caused by rising global temperatures contributes significantly to sea level rise.

A cracked asphalt road with a pothole.
Figure 94.5: Thermal stress contributes to the formation of potholes, as seen in roads that experience daily or seasonal temperature cycles. (credit: Editor5807, Wikimedia Commons)

Thermal Stress in the Human Body and Medicine

Metals are frequently used in biomedical applications, such as in hip and knee prosthetics. However, metals typically do not bond well with bone. Researchers are exploring metal coatings that promote bone growth and adhesion. One important design consideration is thermal compatibility: if the thermal expansion coefficient of the coating is significantly different from that of the metal, internal stresses can develop during cooling after manufacturing. These stresses can lead to microscopic cracks and eventual failure of the implant coating.

Another example of thermal stress is found in dentistry. Traditional metal fillings (e.g., silver, gold) expand more than tooth enamel when exposed to heat. This mismatch can lead to pain when consuming hot or cold food and beverages. Over time, these expansion mismatches may cause fillings to crack or loosen. Newer composite materials, such as porcelain-based fillings, are favored because their expansion properties more closely match those of natural teeth, reducing thermal stress and discomfort.

Check Your Understanding

Two blocks, A and B, are made of the same material. Block A has dimensions [latex]L \times 2L \times L[/latex], and Block B has dimensions [latex]2L \times 2L \times 2L[/latex]. If the temperature changes, determine the relative changes in:

  1. Volume
  2. Cross-sectional area [latex]L \times 2L[/latex]
  3. Height [latex]h[/latex]
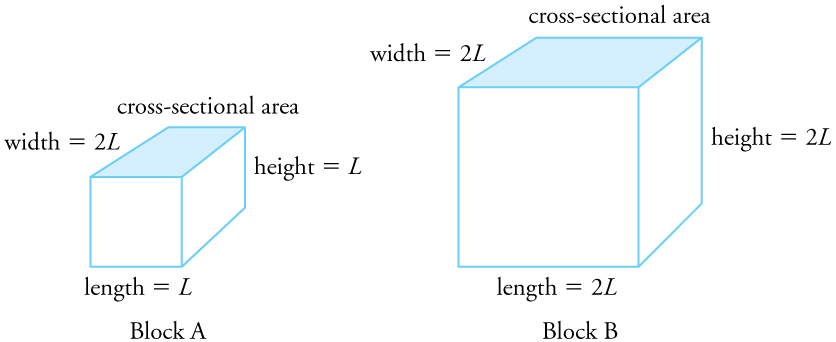
There are two rectangular blocks. Block A has its dimensions labeled length equals L, width equals two times L, height equals L. Block B has its dimensions labeled length, width, and height all equal to two times L.
Figure 94.6 Comparing thermal expansion in blocks of different sizes but identical material properties.

(a) Volume: The volume of Block A is [latex]2L^3[/latex]; Block B is [latex]8L^3[/latex]. Since thermal expansion is proportional to original volume, Block B will experience four times the volume change of Block A.

(b) Cross-sectional area: Block A’s cross-sectional area is [latex]2L^2[/latex], while Block B’s is [latex]4L^2[/latex]. Thus, the change in area for Block B is twice that of Block A.

(c) Height: The original height of Block B is twice that of Block A, so the change in height for Block B will be twice that of Block A.

Section Summary

  • Thermal expansion refers to the change in size—length, area, or volume—of a material as a result of temperature change.
  • Expansion is more significant in gases than in liquids or solids, but all states of matter expand with increasing temperature (with rare exceptions like water).
  • Linear thermal expansion is described by:
    [latex]\Delta L = \alpha L \Delta T[/latex]
  • Area expansion is given by:
    [latex]\Delta A = 2\alpha A \Delta T[/latex]
  • Volume expansion is given by:
    [latex]\Delta V = \beta V \Delta T[/latex]

    where [latex]\beta \approx 3\alpha[/latex].

  • When expansion or contraction is constrained, internal thermal stresses develop, which can damage materials or biological structures.

Conceptual Questions

  1. Thermal stresses caused by uneven cooling can easily break glass cookware. Explain why Pyrex®, a glass with a small coefficient of linear expansion, is less susceptible.
  2. Water expands significantly when it freezes: a volume increase of about 9% occurs. As a result of this expansion and because of the formation and growth of crystals as water freezes, anywhere from 10% to 30% of biological cells are burst when animal or plant material is frozen. Discuss the implications of this cell damage for the prospect of preserving human bodies by freezing so that they can be thawed at some future date when it is hoped that all diseases are curable.
  3. One method of getting a tight fit, say of a metal peg in a hole in a metal block, is to manufacture the peg slightly larger than the hole. The peg is then inserted when at a different temperature than the block. Should the block be hotter or colder than the peg during insertion? Explain your answer.
  4. Does it really help to run hot water over a tight metal lid on a glass jar before trying to open it? Explain your answer.
  5. Liquids and solids expand with increasing temperature, because the kinetic energy of a body’s atoms and molecules increases. Explain why some materials shrink with increasing temperature.

Problems & Exercises

  1. The height of the Washington Monument is measured to be 170 m on a day when the temperature is [latex]\text{35}\text{.}0\text{º}\text{C}[/latex]. What will its height be on a day when the temperature falls to [latex]–\text{10}\text{.}0\text{º}\text{C}[/latex]? Although the monument is made of limestone, assume that its thermal coefficient of expansion is the same as marble’s.
  2. How much taller does the Eiffel Tower become at the end of a day when the temperature has increased by [latex]\text{15}\text{º}\text{C}[/latex]? Its original height is 321 m and you can assume it is made of steel.
  3. What is the change in length of a 3.00-cm-long column of mercury if its temperature changes from [latex]\text{37}\text{.}0\text{º}\text{C}[/latex] to [latex]\text{40}\text{.}0\text{º}\text{C}[/latex], assuming the mercury is unconstrained?
  4. How large an expansion gap should be left between steel railroad rails if they may reach a maximum temperature [latex]\text{35}\text{.}0\text{º}\text{C}[/latex] greater than when they were laid? Their original length is 10.0 m.
  5. You are looking to purchase a small piece of land in Hong Kong. The price is “only” ?60,000 per square meter! The land title says the dimensions are [latex]\text{20}\phantom{\rule{0.25em}{0ex}}\text{m}\phantom{\rule{0.20em}{0ex}}×\phantom{\rule{0.20em}{0ex}}\text{30 m}\text{.}[/latex] By how much would the total price change if you measured the parcel with a steel tape measure on a day when the temperature was [latex]\text{20}\text{º}\text{C}[/latex] above normal?
  6. Global warming will produce rising sea levels partly due to melting ice caps but also due to the expansion of water as average ocean temperatures rise. To get some idea of the size of this effect, calculate the change in length of a column of water 1.00 km high for a temperature increase of [latex]1\text{.}\text{00}\text{º}\text{C}\text{.}[/latex] Note that this calculation is only approximate because ocean warming is not uniform with depth.Show that 60.0 L of gasoline originally at [latex]\text{15}\text{.}0\text{º}\text{C}[/latex] will expand to 61.1 L when it warms to [latex]\text{35}\text{.}0\text{º}\text{C,}[/latex] as claimed in Example 94.2.
  7. (a) Suppose a meter stick made of steel and one made of invar (an alloy of iron and nickel) are the same length at [latex]0\text{º}\text{C}[/latex]. What is their difference in length at [latex]\text{22}\text{.}0\text{º}\text{C}[/latex]? (b) Repeat the calculation for two 30.0-m-long surveyor’s tapes.
  8. (a) If a 500-mL glass beaker is filled to the brim with ethyl alcohol at a temperature of [latex]5\text{.}\text{00}\text{º}\text{C,}[/latex] how much will overflow when its temperature reaches [latex]\text{22}\text{.}0\text{º}\text{C}[/latex]? (b) How much less water would overflow under the same conditions?
  9. Most automobiles have a coolant reservoir to catch radiator fluid that may overflow when the engine is hot. A radiator is made of copper and is filled to its 16.0-L capacity when at [latex]\text{10}\text{.}0º\text{C}\text{.}[/latex] What volume of radiator fluid will overflow when the radiator and fluid reach their [latex]\text{95}\text{.}0º\text{C}[/latex] operating temperature, given that the fluid’s volume coefficient of expansion is [latex]\beta =\text{400}×{\text{10}}^{–6}/\text{º}\text{C}[/latex]? Note that this coefficient is approximate, because most car radiators have operating temperatures of greater than [latex]\text{95}\text{.}0\text{º}\text{C}\text{.}[/latex]
  10. A physicist makes a cup of instant coffee and notices that, as the coffee cools, its level drops 3.00 mm in the glass cup. Show that this decrease cannot be due to thermal contraction by calculating the decrease in level if the [latex]\text{350}\phantom{\rule{0.25em}{0ex}}{\text{cm}}^{3}[/latex] of coffee is in a 7.00-cm-diameter cup and decreases in temperature from [latex]\text{95}\text{.}0\text{º}\text{C}\phantom{\rule{0.25em}{0ex}}[/latex]to[latex]\phantom{\rule{0.25em}{0ex}}\text{45}\text{.}0\text{º}\text{C}\text{.}[/latex] (Most of the drop in level is actually due to escaping bubbles of air.)
  11. (a) The density of water at [latex]0\text{º}\text{C}[/latex] is very nearly [latex]\text{1000}\phantom{\rule{0.25em}{0ex}}{\text{kg/m}}^{3}[/latex] (it is actually [latex]9\text{99}\text{.}{\text{84 kg/m}}^{3}[/latex]), whereas the density of ice at [latex]0\text{º}\text{C}[/latex] is [latex]9{\text{17 kg/m}}^{3}[/latex]. Calculate the pressure necessary to keep ice from expanding when it freezes, neglecting the effect such a large pressure would have on the freezing temperature. (This problem gives you only an indication of how large the forces associated with freezing water might be.) (b) What are the implications of this result for biological cells that are frozen?
  12. Show that [latex]\beta \approx 3\alpha ,[/latex] by calculating the change in volume [latex]\text{Δ}V[/latex] of a cube with sides of length [latex]L\text{.}[/latex]
  13. We know how the length changes with temperature: [latex]\text{Δ}L={\mathrm{\alpha L}}_{0}\text{Δ}T[/latex]. Also we know that the volume of a cube is related to its length by [latex]V={L}^{3}[/latex], so the final volume is then [latex]V={V}_{0}+\text{Δ}V={\left({L}_{0}+\text{Δ}L\right)}^{3}[/latex]. Substituting for [latex]\text{Δ}L[/latex] gives

Footnotes

  1. 1 Values for liquids and gases are approximate.

Glossary

thermal expansion
the change in size or volume of an object with change in temperature
coefficient of linear expansion
[latex]\alpha[/latex], the change in length, per unit length, per [latex]1\text{º}\text{C}[/latex] change in temperature; a constant used in the calculation of linear expansion; the coefficient of linear expansion depends on the material and to some degree on the temperature of the material
coefficient of volume expansion
[latex]\beta[/latex], the change in volume, per unit volume, per [latex]1\text{º}\text{C}[/latex] change in temperature
thermal stress
stress caused by thermal expansion or contraction
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book