"

Fluid Dynamics and Its Biological and Medical Applications

89 The Onset of Turbulence

Learning Objectives

  • Calculate the Reynolds number for fluid flow in a vessel or tube.
  • Interpret the Reynolds number to determine whether flow is laminar or turbulent.

Predicting Laminar and Turbulent Flow

In fluid systems—such as blood flow in the circulatory system or airflow through the respiratory tract—knowing whether flow is laminar or turbulent is important for understanding how substances are transported.

Laminar flow typically occurs at lower speeds and in smooth tubes or vessels, where fluid moves in parallel layers without mixing. In contrast, turbulence arises at higher velocities or around obstructions, with swirling motion and chaotic mixing.

Interestingly, in the range between clearly laminar and fully turbulent flow, the behavior can be unpredictable. Flow may alternate between smooth and chaotic, depending on local conditions such as vessel geometry and surface roughness.

A narrowing of a blood vessel—called an occlusion—can disrupt smooth blood flow and induce turbulence. As shown in Figure 89.1, the sudden reduction in vessel diameter increases velocity and disturbs flow. This turbulence is not just a theoretical concept—it has real clinical significance. For example, turbulent flow in partially collapsed arteries produces audible vibrations called Korotkoff sounds, which are used in blood pressure measurements. Other clinical examples of turbulence include:

Aneurysms: Balloon-like bulges in arterial walls can cause turbulent blood flow, detectable with a stethoscope.

Heart murmurs: These are sounds from turbulent flow across malfunctioning heart valves.

Ultrasound imaging: Turbulent flow patterns can be visualized using Doppler ultrasound, similar to how meteorologists detect storm movement with radar.

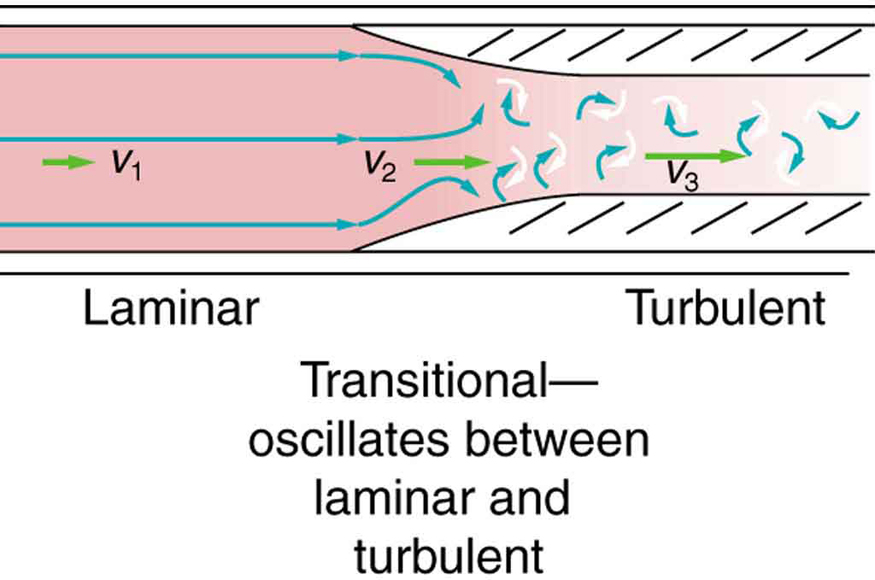
Figure shows a rectangular section of a blood vessel. The blood flow is shown toward right. The blood vessel is shown to be broader at one end and narrow toward the opposite end. The flow is shown to be laminar as shown by horizontal parallel lines. The velocity is v one in the broader section of blood vessel. The junction where the tube narrows the velocity is v two. The lines of flow are shown to bend. The regions where the blood vessels are narrow, the flow is shown to be turbulent as shown to by curling arrows. The velocity is given by v three toward right. The length of the arrows depicting the velocities represent that v three is greater than v two greater than v one.
Figure 89.1 Blood flow is laminar in the wide section of this vessel but becomes turbulent where the vessel narrows due to plaque. In the transition region, flow may oscillate chaotically between laminar and turbulent behavior.

The Reynolds Number

To predict the nature of fluid flow, we use a dimensionless number called the Reynolds number, denoted [latex]N_R[/latex]. For flow through a cylindrical tube such as an artery, it is defined as:

[latex]N_R = \frac{2\rho v r}{\eta}[/latex]

Where:

[latex]\rho[/latex] is the fluid density (e.g., blood density),

[latex]v[/latex] is the average flow speed,

[latex]r[/latex] is the radius of the tube or vessel,

[latex]\eta[/latex] is the dynamic viscosity of the fluid.

The Reynolds number helps classify flow behavior:

If [latex]N_R 2000[/latex], the flow is generally laminar. If [latex]N_R > 3000[/latex], the flow is generally turbulent.

Between 2000 and 3000, flow is unstable and can alternate unpredictably between the two types.

In the human body, most blood flow remains laminar due to relatively low velocities and smooth vessel walls. However, in large arteries like the aorta, blood can reach velocities high enough (above 35 cm/s) to induce turbulence. The transition from laminar to turbulent flow in such cases can have diagnostic implications in cardiology and vascular medicine.

Example 89.1 Is This Flow Laminar or Turbulent?

Calculate the Reynolds number for flow in the needle considered in Example 88.2 to verify the assumption that the flow is laminar. Assume that the density of the saline solution is [latex]1025 kg/{\text{m}}^{3}[/latex].

Strategy

We have all of the information needed, except the fluid speed [latex]v[/latex], which can be calculated from [latex]\overline{v}=Q/A=1.70 m/s[/latex] (verification of this is in this chapter’s Problems and Exercises).

Solution

Entering the known values into [latex]{N}_{\text{R}}=\frac{2\rho \text{vr}}{\eta }[/latex] gives

[latex]\begin{array}{lll}{N}_{\text{R}}& =& \frac{2\rho \text{vr}}{\eta }\\ & =& \frac{2\left({\text{1025 kg/m}}^{3}\right)\left(\text{1.70 m/s}\right)\left(0.150×{\text{10}}^{-3}\phantom{\rule{0.25em}{0ex}}\text{m}\right)}{1\text{.}\text{00}×{\text{10}}^{-3}\phantom{\rule{0.25em}{0ex}}\text{N}\cdot {\text{s/m}}^{2}}\\ & =& \text{523}\text{.}\end{array}[/latex]

Discussion

Since [latex]{N}_{\text{R}}[/latex] is well below 2000, the flow should indeed be laminar.

Take-Home Experiment: Inhalation

During normal breathing at rest, an adult typically inhales about 1 liter (1 L) of air per breath. You can estimate your own average inhalation flow rate using this simple experiment:

  1. Use a stopwatch or watch with a second hand to time how long it takes you to complete several normal breaths (e.g., 5–10).
  2. Divide the total time by the number of breaths to find your average duration per inhalation.
  3. Use the flow rate formula:
    [latex]Q = \frac{V}{t}[/latex]

    where:

    • [latex]Q[/latex] is the average volumetric flow rate,
    • [latex]V[/latex] is the inhaled volume (1 L or 0.001 m³),
    • [latex]t[/latex] is the average time per inhalation.

    The result will give you the average airflow through your trachea in units of m³/s.

This experiment helps illustrate how human respiration involves measurable fluid dynamics.

Chaotic Flow and Sensitive Dependence

In fluid systems, behavior can become unpredictable under certain conditions. A system is said to be chaotic when its response to small changes in initial conditions is extremely sensitive—so much so that long-term predictions become nearly impossible.

A classic example of this is fluid flow when the Reynolds number lies between 2000 and 3000. In this range, flow may unpredictably shift between laminar and turbulent, depending on minor factors like wall roughness or tiny obstructions.

This phenomenon, known as sensitive dependence on initial conditions, is a key characteristic of chaos. Similar behavior appears in systems as diverse as:

Blood flow in constricted vessels,

The erratic orbit of Pluto,

Irregular cardiac rhythms (arrhythmias).

Despite their differences, these systems can be analyzed using similar mathematical tools developed in the field of chaos theory.

Section Summary

  • The Reynolds number is a dimensionless value that predicts whether fluid flow is laminar or turbulent:
    [latex]N_R = \frac{2\rho v r}{\eta}[/latex]

    where [latex]\rho[/latex] is fluid density, [latex]v[/latex] is speed, [latex]r[/latex] is tube radius, and [latex]\eta[/latex] is viscosity.

  • For [latex]N_R 2000[/latex], flow is typically laminar.
  • For [latex]N_R > 3000[/latex], flow is typically turbulent.
  • Between these values, flow is unstable and may transition unpredictably between both states.

Conceptual Questions

  1. Doppler ultrasound can be used to measure the speed of blood in the body. If there is a partial constriction of an artery, where would you expect blood speed to be greatest, at or nearby the constriction? What are the two distinct causes of higher resistance in the constriction?
  2. Sink drains often have a device such as that shown in Figure 89.2 to help speed the flow of water. How does this work?
    Shows a picture of a small ring shaped section of a cylinder. It is shown to be partitioned in to four equal portions.
    Figure 89.2 You will find devices such as this in many drains. They significantly increase flow rate.
  3. Some ceiling fans have decorative wicker reeds on their blades. Discuss whether these fans are as quiet and efficient as those with smooth blades.

Problems & Exercises

  1. Verify that the flow of oil is laminar (barely) for an oil gusher that shoots crude oil 25.0 m into the air through a pipe with a 0.100-m diameter. The vertical pipe is 50 m long. Take the density of the oil to be [latex]\text{900 kg}{\text{/m}}^{3}[/latex] and its viscosity to be [latex]1.00\phantom{\rule{0.25em}{0ex}}\left({\text{N/m}}^{2}\right)\cdot \text{s}[/latex] (or [latex]1.00 Pa\cdot \text{s}[/latex]).
  2. Show that the Reynolds number [latex]{N}_{\text{R}}[/latex] is unitless by substituting units for all the quantities in its definition and cancelling.
  3. Calculate the Reynolds numbers for the flow of water through (a) a nozzle with a radius of 0.250 cm and (b) a garden hose with a radius of 0.900 cm, when the nozzle is attached to the hose. The flow rate through hose and nozzle is 0.500 L/s. Can the flow in either possibly be laminar?
  4. A fire hose has an inside diameter of 6.40 cm. Suppose such a hose carries a flow of 40.0 L/s starting at a gauge pressure of [latex]1\text{.}\text{62}×{\text{10}}^{6}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}[/latex]. The hose goes 10.0 m up a ladder to a nozzle having an inside diameter of 3.00 cm. Calculate the Reynolds numbers for flow in the fire hose and nozzle to show that the flow in each must be turbulent.
  5. Concrete is pumped from a cement mixer to the place it is being laid, instead of being carried in wheelbarrows. The flow rate is 200.0 L/min through a 50.0-m-long, 8.00-cm-diameter hose, and the pressure at the pump is [latex]8\text{.}\text{00}×{\text{10}}^{6}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}[/latex]. Verify that the flow of concrete is laminar taking concrete’s viscosity to be
  6. At what flow rate might turbulence begin to develop in a water main with a 0.200-m diameter? Assume a [latex]\text{20º C}[/latex] temperature.
  7. What is the greatest average speed of blood flow at [latex]\text{37º C}[/latex] in an artery of radius 2.00 mm if the flow is to remain laminar? What is the corresponding flow rate? Take the density of blood to be [latex]1025 kg/{\text{m}}^{3}[/latex].
  8. In Take-Home Experiment: Inhalation, we measured the average flow rate [latex]Q[/latex] of air traveling through the trachea during each inhalation. Now calculate the average air speed in meters per second through your trachea during each inhalation. The radius of the trachea in adult humans is approximately [latex]{\text{10}}^{-2}\phantom{\rule{0.25em}{0ex}}\text{m}[/latex]. From the data above, calculate the Reynolds number for the air flow in the trachea during inhalation. Do you expect the air flow to be laminar or turbulent?
  9. Gasoline is piped underground from refineries to major users. The flow rate is [latex]3\text{.}\text{00}×{\text{10}}^{–2}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{3}\text{/s}[/latex] (about 500 gal/min), the viscosity of gasoline is [latex]1.00×{\text{10}}^{–3}\phantom{\rule{0.25em}{0ex}}\left({\text{N/m}}^{2}\right)\cdot \text{s}[/latex], and its density is [latex]\text{680}\phantom{\rule{0.25em}{0ex}}{\text{kg/m}}^{3}[/latex]. (a) What minimum diameter must the pipe have if the Reynolds number is to be less than 2000? (b) What pressure difference must be maintained along each kilometer of the pipe to maintain this flow rate?
  10. Assuming that blood is an ideal fluid, calculate the critical flow rate at which turbulence is a certainty in the aorta. Take the diameter of the aorta to be 2.50 cm. (Turbulence will actually occur at lower average flow rates, because blood is not an ideal fluid. Furthermore, since blood flow pulses, turbulence may occur during only the high-velocity part of each heartbeat.)
  11. Unreasonable Results A fairly large garden hose has an internal radius of 0.600 cm and a length of 23.0 m. The nozzleless horizontal hose is attached to a faucet, and it delivers 50.0 L/s. (a) What water pressure is supplied by the faucet? (b) What is unreasonable about this pressure? (c) What is unreasonable about the premise? (d) What is the Reynolds number for the given flow? (Take the viscosity of water as [latex]1.005×{10}^{–3}\phantom{\rule{0.25em}{0ex}}\left(\text{N}/{m}^{2}\right)\cdot \text{s}[/latex].)

Glossary

Reynolds number
a dimensionless parameter that can reveal whether a particular flow is laminar or turbulent
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book