Temperature, Kinetic Theory, and the Gas Laws
95 The Ideal Gas Law
Understanding Gases and the Ideal Gas Law
Learning Objectives
- State the ideal gas law in terms of molecules and in terms of moles.
- Use the ideal gas law to calculate pressure, temperature, volume, or quantity of gas.
- Convert between number of molecules and number of moles using Avogadro’s number.

Gases play vital roles in our bodies and the environment. From the oxygen we breathe to the carbon dioxide we exhale, gases are essential to physiological function and global ecosystems. Understanding how pressure, temperature, and volume relate in gases helps us explain processes ranging from respiration to balloon inflation.
Gas Behavior and Expansion
Gases are highly compressible and exhibit large thermal expansion coefficients. This means they expand and contract significantly with temperature changes. Remarkably, most gases expand at nearly the same rate under similar conditions, unlike solids and liquids, which vary widely. This similarity arises from the large distances between gas molecules compared to their size (see Figure 95.2), meaning intermolecular forces are negligible in many cases.
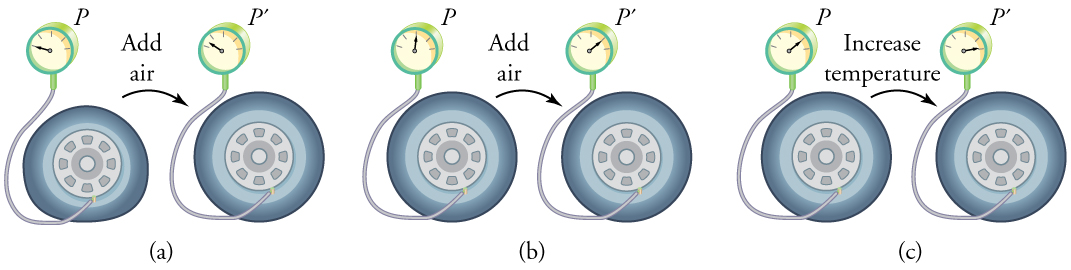
Real-World Example: Inflating a Tire
When air is pumped into a deflated tire, its volume initially increases with little change in pressure. As the tire fills, the volume becomes constrained by the tire walls, and further pumping increases the pressure. If the temperature of the tire also increases—such as from driving—the pressure rises further. This is why tire pressure should be checked when the tires are cold. (Figure 95.3)
The Ideal Gas Law
In many situations, particularly at moderate temperatures and pressures, gases behave in predictable ways that are well described by the ideal gas law. An ideal gas is one in which the particles are small relative to the distance between them and interact only via elastic collisions. Under these assumptions, the relationship between pressure, volume, and temperature is given by:
Where:
- [latex]P[/latex] is the absolute pressure in pascals (Pa)
- [latex]V[/latex] is the volume in cubic meters (m³)
- [latex]N[/latex] is the number of molecules or atoms
- [latex]T[/latex] is the absolute temperature in kelvin (K)
- [latex]k[/latex] is the Boltzmann constant, defined as:
The ideal gas law originates from combining two empirical relationships:
- Charles’s Law: Volume is proportional to temperature at constant pressure
- Boyle’s Law: Pressure times volume is constant at constant temperature
Returning to our tire example, initially the pressure [latex]P[/latex] remains nearly constant while [latex]V[/latex] increases with more gas molecules [latex]N[/latex]. Once the volume is fixed, pressure increases as more gas is added. If temperature rises (e.g., after driving), pressure increases again due to the direct proportionality in the ideal gas law.
Example 95.1: Calculating Pressure Changes Due to Temperature Changes: Tire Pressure
Suppose your bicycle tire is fully inflated, with an absolute pressure of [latex]7\text{.}\text{00}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{Pa}[/latex] (a gauge pressure of just under [latex]\text{90}\text{.}0\phantom{\rule{0.25em}{0ex}}{\text{lb/in}}^{2}[/latex]) at a temperature of [latex]\text{18}\text{.}0\text{º}\text{C}[/latex]. What is the pressure after its temperature has risen to [latex]\text{35}\text{.}0\text{º}\text{C}[/latex]? Assume that there are no appreciable leaks or changes in volume.
Strategy
The pressure in the tire is changing only because of changes in temperature. First we need to identify what we know and what we want to know, and then identify an equation to solve for the unknown.
We know the initial pressure [latex]{P}_{0}=7\text{.00}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{Pa}[/latex], the initial temperature
[latex]{T}_{0}=\text{18}\text{.}0ºC[/latex], and the final temperature
[latex]{T}_{\text{f}}=35\text{.}0ºC[/latex]. We must find the final pressure
[latex]{P}_{\text{f}}[/latex]. How can we use the equation
[latex]\text{PV}=\text{NkT}[/latex]? At first, it may seem that not enough information is given, because the volume
[latex]V[/latex] and number of atoms
[latex]N[/latex] are not specified. What we can do is use the equation twice:
[latex]{P}_{0}{V}_{0}={\text{NkT}}_{0}[/latex] and
[latex]{P}_{\text{f}}{V}_{\text{f}}={\text{NkT}}_{\text{f}}[/latex]. If we divide
[latex]{P}_{\text{f}}{V}_{\text{f}}[/latex] by
[latex]{P}_{0}{V}_{0}[/latex] we can come up with an equation that allows us to solve for
[latex]{P}_{\text{f}}[/latex].
Since the volume is constant, [latex]{V}_{\text{f}}[/latex] and [latex]{V}_{0}[/latex] are the same and they cancel out. The same is true for [latex]{N}_{\text{f}}[/latex] and [latex]{N}_{0}[/latex], and [latex]k[/latex], which is a constant. Therefore,
We can then rearrange this to solve for [latex]{P}_{\text{f}}[/latex]:
where the temperature must be in units of kelvins, because [latex]{T}_{0}[/latex] and [latex]{T}_{\text{f}}[/latex] are absolute temperatures.
Solution
- Convert temperatures from Celsius to Kelvin.
[latex]\begin{array}{}{T}_{0}=\left(\text{18}\text{.}0+\text{273}\right)\text{K}=\text{291 K}\\ {T}_{\text{f}}=\left(\text{35}\text{.}0+\text{273}\right)\text{K}=\text{308 K}\end{array}[/latex] - Substitute the known values into the equation.
[latex]{P}_{\text{f}}={P}_{0}\frac{{T}_{\text{f}}}{{T}_{0}}=7\text{.}\text{00}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{Pa}\left(\frac{\text{308 K}}{\text{291 K}}\right)=7\text{.}\text{41}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{Pa}[/latex]
Discussion
The final temperature is about 6% greater than the original temperature, so the final pressure is about 6% greater as well. Note that absolute pressure and absolute temperature must be used in the ideal gas law.
Making Connections: Take-Home Experiment—Refrigerating a Balloon
Inflate a balloon at room temperature. Leave the inflated balloon in the refrigerator overnight. What happens to the balloon, and why?
Example 95.2: Calculating the Number of Molecules in a Cubic Meter of Gas
How many molecules are in a typical object, such as gas in a tire or water in a drink? We can use the ideal gas law to give us an idea of how large [latex]N[/latex] typically is.
Calculate the number of molecules in a cubic meter of gas at standard temperature and pressure (STP), which is defined to be [latex]0\text{º}\text{C}[/latex] and atmospheric pressure.
Strategy
Because pressure, volume, and temperature are all specified, we can use the ideal gas law [latex]\text{PV}=\text{NkT}[/latex], to find [latex]N[/latex].
Solution
- Identify the knowns.
[latex]\begin{array}{lll}T& =& 0\text{º}\text{C}=\text{273 K}\\ P& =& 1\text{.}\text{01}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{Pa}\\ V& =& 1\text{.}\text{00}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{3}\\ k& =& 1\text{.}\text{38}×{\text{10}}^{-\text{23}}\phantom{\rule{0.25em}{0ex}}\text{J/K}\end{array}[/latex] - Identify the unknown: number of molecules, [latex]N[/latex].
- Rearrange the ideal gas law to solve for [latex]N[/latex].
[latex]\begin{array}{}\text{PV}=\text{NkT}\\ N=\frac{\text{PV}}{\text{kT}}\end{array}[/latex] - Substitute the known values into the equation and solve for [latex]N[/latex].
[latex]N=\frac{\text{PV}}{\text{kT}}=\frac{\left(1\text{.}\text{01}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{Pa}\right)\left(1\text{.}{\text{00 m}}^{3}\right)}{\left(1\text{.}\text{38}×{\text{10}}^{-\text{23}}\phantom{\rule{0.25em}{0ex}}\text{J/K}\right)\left(\text{273 K}\right)}=2\text{.}\text{68}×{\text{10}}^{\text{25}}\phantom{\rule{0.25em}{0ex}}\text{molecules}[/latex]
Discussion
This number is undeniably large, considering that a gas is mostly empty space. [latex]N[/latex] is huge, even in small volumes. For example, [latex]1\phantom{\rule{0.25em}{0ex}}{\text{cm}}^{3}[/latex] of a gas at STP has [latex]2\text{.}\text{68}×{\text{10}}^{\text{19}}[/latex] molecules in it. Once again, note that [latex]N[/latex] is the same for all types or mixtures of gases.
Moles and Avogadro’s Number
In biology and chemistry, we often work with enormous numbers of molecules—far too many to count individually. To simplify things, scientists use a unit called the mole (mol). A mole is defined as the number of atoms in exactly 12 grams of carbon-12. That number, known as Avogadro’s number, is:
Whether you’re measuring water molecules, proteins, or drug compounds, one mole always contains [latex]6.02 \times 10^{23}[/latex] particles. This allows scientists to translate easily between microscopic particle counts and macroscopic quantities of mass in grams.
Mass of One Mole
One mole of a substance has a mass in grams equal to its molecular mass or molar mass, calculated by summing the atomic masses of its atoms using the periodic table. For example, the molar mass of water [latex]\text{H}_2\text{O}[/latex] is approximately 18 grams per mole.
Avogadro’s Number
One mole of any substance contains exactly:
This quantity is independent of the type of molecule or atom.
Biomedical Example: Acetaminophen Dosage
Check Your Understanding
The active ingredient in a Tylenol® tablet is 325 mg of acetaminophen ([latex]\text{C}_8\text{H}_9\text{NO}_2[/latex]). How many individual molecules of acetaminophen are in one dose?
Step 1: Calculate the molar mass of acetaminophen.
Step 2: Convert 325 mg to grams and calculate the number of moles.
Step 3: Use Avogadro’s number to find the number of molecules.
So, one Tylenol® tablet contains about [latex]1.3 \times 10^{21}[/latex] acetaminophen molecules.
Example 95.3: Calculating Moles per Cubic Meter and Liters per Mole
Calculate: (a) the number of moles in [latex]1\text{.}\text{00}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{3}[/latex] of gas at STP, and (b) the number of liters of gas per mole.
Strategy and Solution
- We are asked to find the number of moles per cubic meter, and we know from Example 95.2 that the number of molecules per cubic meter at STP is [latex]2\text{.}\text{68}×{\text{10}}^{\text{25}}[/latex]. The number of moles can be found by dividing the number of molecules by Avogadro’s number. We let [latex]n[/latex] stand for the number of moles,
[latex]n\phantom{\rule{0.25em}{0ex}}{\text{mol/m}}^{3}=\frac{N\phantom{\rule{0.25em}{0ex}}{\text{molecules/m}}^{3}}{6\text{.}\text{02}×{\text{10}}^{\text{23}}\phantom{\rule{0.25em}{0ex}}\text{molecules/mol}}=\frac{2\text{.}\text{68}×{\text{10}}^{\text{25}}\phantom{\rule{0.25em}{0ex}}{\text{molecules/m}}^{3}}{6\text{.}\text{02}×{\text{10}}^{\text{23}}\phantom{\rule{0.25em}{0ex}}\text{molecules/mol}}=\text{44}\text{.}5\phantom{\rule{0.25em}{0ex}}{\text{mol/m}}^{3}\text{.}[/latex] - Using the value obtained for the number of moles in a cubic meter, and converting cubic meters to liters, we obtain
[latex]\frac{\left({\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}{\text{L/m}}^{3}\right)}{44\text{.}5\phantom{\rule{0.25em}{0ex}}{\text{mol/m}}^{3}}=\text{22}\text{.}5\phantom{\rule{0.25em}{0ex}}\text{L/mol}\text{.}[/latex]
Discussion
This value is very close to the accepted value of 22.4 L/mol. The slight difference is due to rounding errors caused by using three-digit input. Again this number is the same for all gases. In other words, it is independent of the gas.
The (average) molar weight of air (approximately 80% [latex]{\text{N}}_{2}[/latex] and 20% [latex]{\text{O}}_{2}[/latex] is [latex]M=\text{28}\text{.}8\phantom{\rule{0.25em}{0ex}}\text{g}\text{.}[/latex] Thus the mass of one cubic meter of air is 1.28 kg. If a living room has dimensions [latex]5\phantom{\rule{0.25em}{0ex}}\text{m}×\text{5 m}×\text{3 m,}[/latex] the mass of air inside the room is 96 kg, which is the typical mass of a human.
Check Your Understanding
The density of air under standard conditions ([latex]P = 1 \ \text{atm}[/latex] and [latex]T = 20^\circ \text{C}[/latex]) is [latex]1.28 \ \text{kg/m}^3[/latex]. What will the pressure be if the air’s density drops to [latex]0.64 \ \text{kg/m}^3[/latex], assuming temperature and number of molecules stay constant?
If the number of molecules stays the same but density drops to half, then the volume must double. From the ideal gas law:
If temperature and number of particles are constant, pressure is inversely proportional to volume. So if volume doubles, pressure must be halved:
This type of reasoning is helpful in respiratory physiology where pressure-volume relationships govern lung expansion and gas exchange.
The Ideal Gas Law Restated Using Moles
In biomedical and chemical applications, it’s often more convenient to describe the quantity of a substance in moles rather than number of molecules. To express the ideal gas law in terms of moles, we begin with:
We then use the definition:
Multiplying and dividing the original equation by Avogadro’s number [latex]N_{\text{A}}[/latex]:
This leads to a new version of the ideal gas law in terms of moles:
Ideal Gas Law (in terms of moles)
The ideal gas law can also be written as:
Here:
- [latex]P[/latex] is pressure
- [latex]V[/latex] is volume
- [latex]n[/latex] is number of moles
- [latex]R[/latex] is the universal gas constant
- [latex]T[/latex] is absolute temperature
The value of [latex]R[/latex] depends on the units you’re using. Some common values include:
You can use whichever form of [latex]R[/latex] fits your problem. In biological systems, pressure might be measured in atmospheres (atm) and volume in liters (L), so [latex]R = 0.0821[/latex] is often convenient.
Example 95.4: Calculating Number of Moles: Gas in a Bike Tire
How many moles of gas are in a bike tire with a volume of [latex]2\text{.}\text{00}×{\text{10}}^{–3}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{3}\left(2\text{.}\text{00 L}\right),[/latex] a pressure of [latex]7\text{.}\text{00}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{Pa}[/latex] (a gauge pressure of just under [latex]\text{90}\text{.}0\phantom{\rule{0.25em}{0ex}}{\text{lb/in}}^{2}[/latex]), and at a temperature of [latex]\text{18}\text{.}0\text{º}\text{C}[/latex]?
Strategy
Identify the knowns and unknowns, and choose an equation to solve for the unknown. In this case, we solve the ideal gas law, [latex]\text{PV}=\text{nRT}[/latex], for the number of moles [latex]n[/latex].
Solution
- Identify the knowns.
[latex]\begin{array}{lll}P& =& 7\text{.}\text{00}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{Pa}\\ V& =& 2\text{.}\text{00}×{\text{10}}^{-3}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{3}\\ T& =& \text{18}\text{.}0\text{º}\text{C}=\text{291 K}\\ R& =& 8\text{.}\text{31}\phantom{\rule{0.25em}{0ex}}\text{J/mol}\cdot \text{K}\end{array}[/latex] - Rearrange the equation to solve for [latex]n[/latex] and substitute known values.
[latex]\begin{array}{lll}n& =& \frac{\text{PV}}{\text{RT}}=\frac{\left(7\text{.}\text{00}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{Pa}\right)\left(2\text{.}00×{\text{10}}^{-3}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{3}\right)}{\left(8\text{.}\text{31}\phantom{\rule{0.25em}{0ex}}\text{J/mol}\cdot \text{K}\right)\left(\text{291}\phantom{\rule{0.25em}{0ex}}\text{K}\right)}\\ \text{}& =& \text{0}\text{.}\text{579}\phantom{\rule{0.25em}{0ex}}\text{mol}\end{array}[/latex]
Discussion
The most convenient choice for [latex]R[/latex] in this case is [latex]8\text{.}\text{31}\phantom{\rule{0.25em}{0ex}}\text{J/mol}\cdot \text{K,}[/latex] because our known quantities are in SI units. The pressure and temperature are obtained from the initial conditions in Example 95.1 , but we would get the same answer if we used the final values.
The Ideal Gas Law and Energy
The ideal gas law can be interpreted as another form of the law of conservation of energy. For example, when you compress a gas (such as pumping air into a bike tire), you’re doing work on the system. This input of energy increases the gas’s internal energy, resulting in higher pressure, temperature, or both.
Let’s analyze the equation:
On the right-hand side, the term [latex]NkT[/latex] represents the total translational kinetic energy of the molecules. This is a key form of internal energy in a gas. The left-hand side, [latex]PV[/latex], also has units of energy (joules), and represents the energy associated with pressure and volume—two measurable macroscopic variables. This reflects how gases store and transfer energy through their molecular motion.
In biological systems—like in the lungs, blood vessels, or medical devices—understanding how gases behave under compression and temperature change is essential for understanding ventilation, oxygen delivery, or even how anesthesia works.
Problem-Solving Strategy: The Ideal Gas Law
- Confirm it’s a gas problem: Most gases behave nearly ideally under normal biological conditions.
- List known quantities: Convert everything into SI units:
- Temperature: kelvins (K)
- Pressure: pascals (Pa)
- Volume: cubic meters ([latex]\text{m}^3[/latex])
- Amount of substance: either molecules ([latex]N[/latex]) or moles ([latex]n[/latex])
- Identify unknowns: Clearly state what you’re solving for.
- Select the correct form:
- [latex]PV = NkT[/latex] for number of molecules
- [latex]PV = nRT[/latex] for number of moles
- Rearrange and solve: Use algebra to isolate the unknown variable.
- Substitute and compute: Plug in values (with units!) and solve.
- Check your result: Does the answer make physical sense?
Check Your Understanding
Liquids and solids are about 1000 times denser than gases. Why does this imply that molecules in gases are approximately 10 times farther apart than in solids and liquids?
In solids and liquids, atoms are tightly packed, leaving very little empty space. In gases, atoms are much farther apart. Since volume scales with the cube of distance, if distance between particles increases by a factor of 10, volume increases by a factor of [latex]10^3 = 1000[/latex]. As a result, the density decreases by the same factor.
Section Summary
- The ideal gas law links pressure, volume, temperature, and amount of gas. It can be written as:
[latex]PV = NkT[/latex]
where:
- [latex]P[/latex] = pressure
- [latex]V[/latex] = volume
- [latex]T[/latex] = temperature (in kelvins)
- [latex]N[/latex] = number of molecules
- [latex]k = 1.38 \times 10^{-23} \ \text{J/K}[/latex] = Boltzmann constant
- A mole is defined as the number of atoms in 12 g of carbon-12.
- Avogadro’s number:
[latex]N_A = 6.02 \times 10^{23} \ \text{mol}^{-1}[/latex]
- The mass of one mole of a substance in grams equals its molecular mass (from the periodic table).
- In terms of moles, the ideal gas law becomes:
[latex]PV = nRT[/latex]
where:
- [latex]n[/latex] = number of moles
- [latex]R = 8.31 \ \text{J/mol·K}[/latex] = universal gas constant
- This law holds well at temperatures significantly above the boiling point of the gas.
Conceptual Questions
- Find out the human population of Earth. Is there a mole of people inhabiting Earth? If the average mass of a person is 60 kg, calculate the mass of a mole of people. How does the mass of a mole of people compare with the mass of Earth?
- Under what circumstances would you expect a gas to behave significantly differently than predicted by the ideal gas law?
- A constant-volume gas thermometer contains a fixed amount of gas. What property of the gas is measured to indicate its temperature?
Problems & Exercises
- The gauge pressure in your car tires is [latex]2\text{.}\text{50}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}[/latex] at a temperature of [latex]\text{35}\text{.}0\text{º}\text{C}[/latex] when you drive it onto a ferry boat to Alaska. What is their gauge pressure later, when their temperature has dropped to [latex]–\text{40}\text{.}0\text{º}\text{C}[/latex]?
- Convert an absolute pressure of [latex]7\text{.}\text{00}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}[/latex] to gauge pressure in [latex]{\text{lb/in}}^{2}\text{.}[/latex] (This value was stated to be just less than [latex]\text{90}\text{.}{\text{0 lb/in}}^{2}[/latex] in Example 95.4. Is it?)
- Suppose a gas-filled incandescent light bulb is manufactured so that the gas inside the bulb is at atmospheric pressure when the bulb has a temperature of [latex]\text{20}\text{.}0\text{º}\text{C}[/latex]. (a) Find the gauge pressure inside such a bulb when it is hot, assuming its average temperature is [latex]\text{60}\text{.}0\text{º}\text{C}[/latex] (an approximation) and neglecting any change in volume due to thermal expansion or gas leaks. (b) The actual final pressure for the light bulb will be less than calculated in part (a) because the glass bulb will expand. What will the actual final pressure be, taking this into account? Is this a negligible difference?
- Large helium-filled balloons are used to lift scientific equipment to high altitudes. (a) What is the pressure inside such a balloon if it starts out at sea level with a temperature of [latex]\text{10}\text{.}0\text{º}\text{C}[/latex] and rises to an altitude where its volume is twenty times the original volume and its temperature is [latex]–\text{50}\text{.}0\text{º}\text{C}[/latex]? (b) What is the gauge pressure? (Assume atmospheric pressure is constant.)
- Confirm that the units of [latex]\text{nRT}[/latex] are those of energy for each value of [latex]R[/latex]: (a) [latex]8\text{.}\text{31}\phantom{\rule{0.25em}{0ex}}\text{J/mol}\cdot \text{K}[/latex], (b) [latex]1\text{.}\text{99 cal/mol}\cdot \text{K}[/latex], and (c) [latex]0\text{.}\text{0821 L}\cdot \text{atm/mol}\cdot \text{K}[/latex].
- In the text, it was shown that [latex]N/V=2\text{.}\text{68}×{\text{10}}^{\text{25}}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{-3}[/latex] for gas at STP. (a) Show that this quantity is equivalent to [latex]N/V=2\text{.}\text{68}×{\text{10}}^{\text{19}}\phantom{\rule{0.25em}{0ex}}{\text{cm}}^{-3},[/latex] as stated. (b) About how many atoms are there in one [latex]{\text{μm}}^{3}[/latex] (a cubic micrometer) at STP? (c) What does your answer to part (b) imply about the separation of atoms and molecules?
- Calculate the number of moles in the 2.00-L volume of air in the lungs of the average person. Note that the air is at [latex]\text{37}\text{.}0\text{º}\text{C}[/latex] (body temperature).
- An airplane passenger has [latex]\text{100}\phantom{\rule{0.25em}{0ex}}{\text{cm}}^{3}[/latex] of air in his stomach just before the plane takes off from a sea-level airport. What volume will the air have at cruising altitude if cabin pressure drops to [latex]7\text{.}\text{50}×{\text{10}}^{4}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}?[/latex]
- (a) What is the volume (in [latex]{\text{km}}^{3}[/latex]) of Avogadro’s number of sand grains if each grain is a cube and has sides that are 1.0 mm long? (b) How many kilometers of beaches in length would this cover if the beach averages 100 m in width and 10.0 m in depth? Neglect air spaces between grains.
- An expensive vacuum system can achieve a pressure as low as [latex]1\text{.}\text{00}×{\text{10}}^{–7}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}[/latex] at [latex]\text{20}\text{º}\text{C}[/latex]. How many atoms are there in a cubic centimeter at this pressure and temperature?
- The number density of gas atoms at a certain location in the space above our planet is about [latex]1\text{.}\text{00}×{\text{10}}^{\text{11}}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{-3},[/latex] and the pressure is [latex]2\text{.}\text{75}×{\text{10}}^{–\text{10}}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}[/latex] in this space. What is the temperature there?
- A bicycle tire has a pressure of [latex]7\text{.}\text{00}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}[/latex] at a temperature of [latex]\text{18}\text{.}0\text{º}\text{C}[/latex] and contains 2.00 L of gas. What will its pressure be if you let out an amount of air that has a volume of [latex]\text{100}\phantom{\rule{0.25em}{0ex}}{\text{cm}}^{3}[/latex] at atmospheric pressure? Assume tire temperature and volume remain constant.
- A high-pressure gas cylinder contains 50.0 L of toxic gas at a pressure of [latex]1\text{.}\text{40}×{\text{10}}^{7}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}[/latex] and a temperature of [latex]\text{25}\text{.}0\text{º}\text{C}[/latex]. Its valve leaks after the cylinder is dropped. The cylinder is cooled to dry ice temperature [latex]\left(–\text{78}\text{.}5\text{º}\text{C}\right)[/latex] to reduce the leak rate and pressure so that it can be safely repaired. (a) What is the final pressure in the tank, assuming a negligible amount of gas leaks while being cooled and that there is no phase change? (b) What is the final pressure if one-tenth of the gas escapes? (c) To what temperature must the tank be cooled to reduce the pressure to 1.00 atm (assuming the gas does not change phase and that there is no leakage during cooling)? (d) Does cooling the tank appear to be a practical solution?
- Find the number of moles in 2.00 L of gas at [latex]\text{35}\text{.}0\text{º}\text{C}[/latex] and under [latex]7\text{.}\text{41}×{\text{10}}^{7}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}[/latex] of pressure.
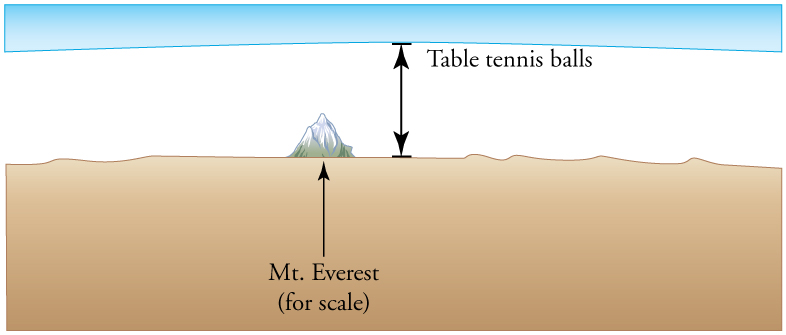
- Calculate the depth to which Avogadro’s number of table tennis balls would cover Earth. Each ball has a diameter of 3.75 cm. Assume the space between balls adds an extra 25.0% to their volume and assume they are not crushed by their own weight.
- (a) What is the gauge pressure in a [latex]\text{25}\text{.}0\text{º}\text{C}[/latex] car tire containing 3.60 mol of gas in a 30.0 L volume? (b) What will its gauge pressure be if you add 1.00 L of gas originally at atmospheric pressure and [latex]\text{25}\text{.}0\text{º}\text{C}[/latex]? Assume the temperature returns to [latex]\text{25}\text{.}0\text{º}\text{C}[/latex] and the volume remains constant.
- (a) In the deep space between galaxies, the density of atoms is as low as [latex]{\text{10}}^{6}\phantom{\rule{0.25em}{0ex}}{\text{atoms/m}}^{3},[/latex] and the temperature is a frigid 2.7 K. What is the pressure? (b) What volume (in [latex]{\text{m}}^{3}[/latex]) is occupied by 1 mol of gas? (c) If this volume is a cube, what is the length of its sides in kilometers?
Glossary
- ideal gas law
- the physical law that relates the pressure and volume of a gas to the number of gas molecules or number of moles of gas and the temperature of the gas
- Boltzmann constant
- [latex]k[/latex] , a physical constant that relates energy to temperature; [latex]k=\text{1.38}×{\text{10}}^{\text{–23}}\phantom{\rule{0.25em}{0ex}}\text{J/K}[/latex]
- Avogadro’s number
- [latex]{N}_{\text{A}}[/latex] , the number of molecules or atoms in one mole of a substance;
[latex]{N}_{\text{A}}=6\text{.}\text{02}×{\text{10}}^{\text{23}}[/latex] particles/mole
- mole
- the quantity of a substance whose mass (in grams) is equal to its molecular mass
the change in size or volume of an object with change in temperature
the physical law that relates the pressure and volume of a gas to the number of gas molecules or number of moles of gas and the temperature of the gas
[latex]k[/latex] , a physical constant that relates energy to temperature; [latex]k=\text{1.38}×{\text{10}}^{\text{–23}}\phantom{\rule{0.25em}{0ex}}\text{J/K}[/latex]
the quantity of a substance whose mass (in grams) is equal to its molecular mass
[latex]{N}_{\text{A}}[/latex] , the number of molecules or atoms in one mole of a substance;
[latex]{N}_{\text{A}}=6\text{.}\text{02}×{\text{10}}^{\text{23}}[/latex] particles/mole
the general law that total energy is constant in any process; energy may change in form or be transferred from one system to another, but the total remains the same
the sum of the kinetic and potential energies of a system’s atoms and molecules

