"

Thermodynamics

109 The First Law of Thermodynamics and Some Simple Processes

Learning Objectives

  • Describe how a simple heat engine operates using the first law of thermodynamics.
  • Differentiate among the key thermodynamic processes: isobaric, isochoric, isothermal, and adiabatic.
  • Compute the total work done during a cyclical thermodynamic process using a PV diagram.
An old photo of a steam turbine at a turbine production plant. People are shown working on the turbine.
Figure 109.1: Since the Industrial Revolution, humans have used heat to do work—before we fully understood the thermodynamic principles involved. Shown here is a steam turbine at Turbinia Works, circa 1911, only six decades after Clausius formally stated the first law of thermodynamics. (credit: public domain)

One of the most transformative applications of heat is its use to do mechanical work, accomplished through devices known as heat engines. These include car engines, power plant turbines, and even the human body during metabolism. The operation of a heat engine is governed by the first law of thermodynamics and is represented schematically in Figure 109.2.

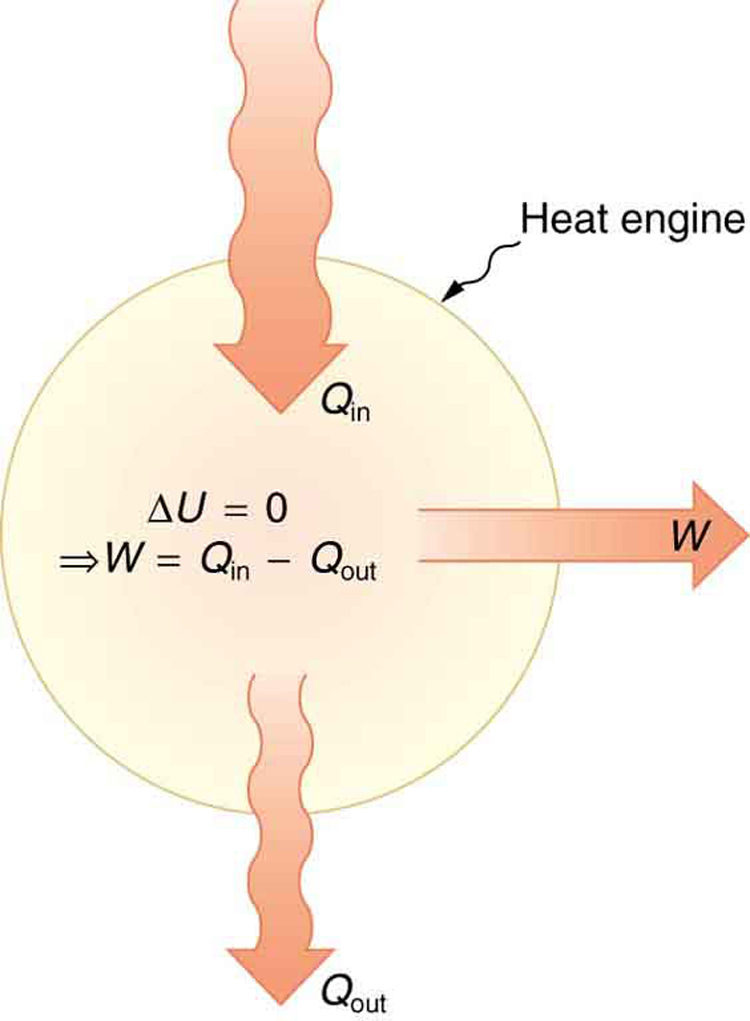
The figure shows a schematic representation of a heat engine. The heat engine is represented by a circle. The heat entering the system is shown as Q sub in, represented as a bold arrow toward the circle, and the heat coming out of the heat engine is shown as Q sub out, represented by a narrower bold arrow leaving the circle. The work labeled as W is shown to leave the heat engine as represented by another bold arrow leaving the circle. At the center of the circle are two equations. First, the change in internal energy of the system, delta U, equals zero. Consequently, W equals Q sub in minus Q sub out.
Figure 109.2A heat engine follows the first law of thermodynamics. Heat [latex]Q_{\text{in}}[/latex] enters the system, some of it is converted to work [latex]W[/latex], and the remaining heat [latex]Q_{\text{out}}[/latex] is expelled to the environment. The net change in internal energy is zero:[latex]\Delta U = 0[/latex]
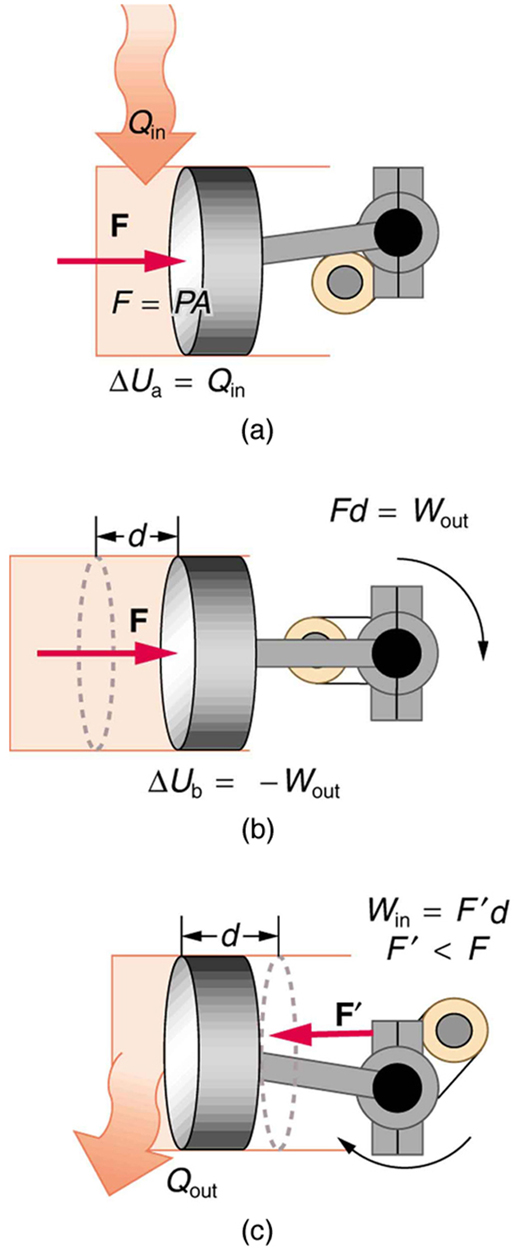
Figure a shows a piston attached to a movable cylinder which is attached to the right of another gas filled cylinder. The heat Q sub in is shown to be transferred to the gas in the cylinder as shown by a bold arrow toward it. The force of the gas on the moving cylinder with the piston is shown as F equals P times A shown as a vector arrow pointing toward the right. The change in internal energy is marked in the diagram as delta U sub a equals Q sub in. Figure b shows a piston attached to a movable cylinder which is attached to the right of another gas filled cylinder. The force of the gas has moved the cylinder with the piston by a distance d toward the right. The change in internal energy is marked in the diagram as delta U sub b equals negative W sub out. The piston is shown to have done work by change in position, marked as F d equal to W sub out. Figure c shows a piston attached to a movable cylinder which is attached to the right of another gas filled cylinder. The piston attached to the cylinder is shown to reach back to the initial position shown in figure a. The distance d is traveled back and heat Q sub out is shown to leave the system as represented by an outward arrow. The force driving backward is shown as a vector arrow pointing to the left, labeled F prime. F prime is shown less than F. The work done by the force F prime is shown by the equation W sub in equal to F prime times d.
Figure 109.3 (a) Heat added to a gas increases its internal energy, raising its pressure. (b) The gas expands, doing work on the piston. (c) Heat is then expelled to return the system to its original state. This cycle is repeated in real-world engines.

In this thermodynamic cycle, heat energy causes gas particles to exert greater pressure. This pressure moves a piston, doing mechanical work. To reset the system, heat is released, lowering the pressure so the piston returns. This forms the basic operation of a heat engine.

PV Diagrams and Work

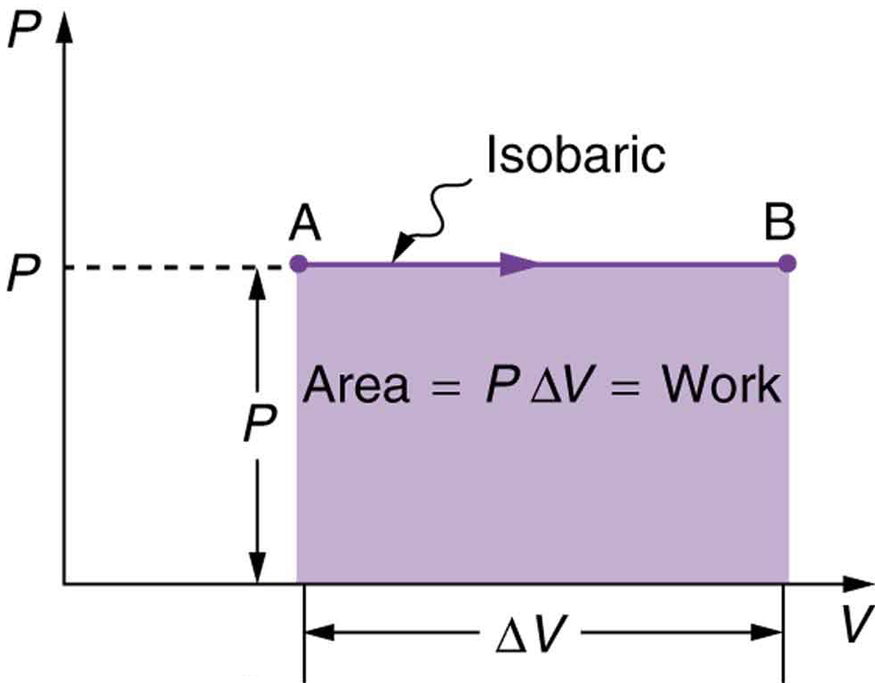
When a gas does work while expanding at constant pressure, the process is called an isobaric process. The work done is the product of pressure and change in volume:

[latex]W = P \Delta V[/latex]
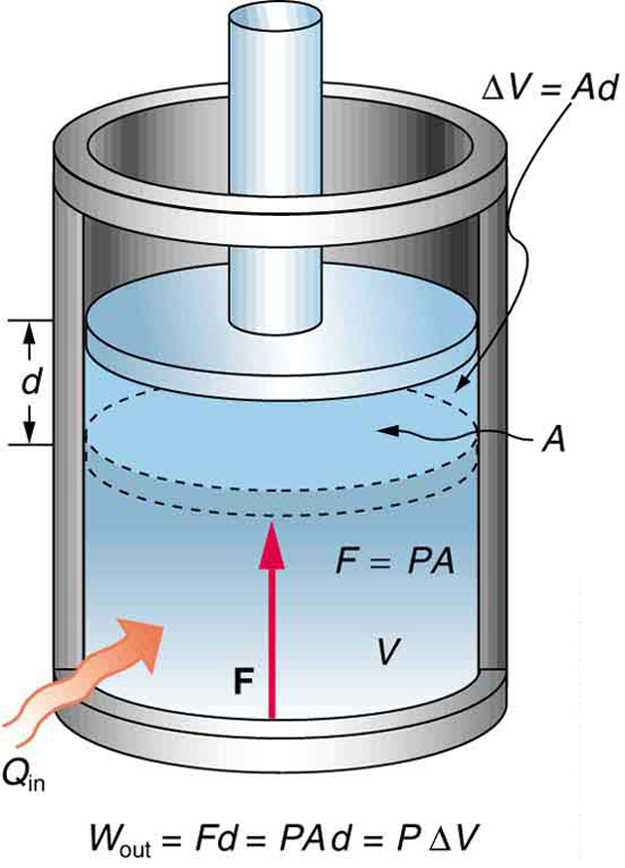
The diagram shows an isobaric expansion of a gas filled cylinder held vertically. V is the volume of gas in the cylinder. A is the area of cross section of the cylinder. The cylinder has a movable piston with a rod attached to it at the top of the cylinder. A heat Q sub in is shown to enter the cylinder from below. A force F equals P times A is shown to act upward from the bottom of the cylinder. The piston is shown to have been displaced by a vertical distance d upward. The volume displaced is given by delta V equals A times d. The work output shown as W sub out is equal to F times d, which is also equal to P times A times d, which in turn equals P times delta V.
Figure 109.4: An isobaric process where heat input maintains constant pressure as the gas expands. The resulting work done by the gas is [latex]W = P \Delta V[/latex].

Since pressure is force per unit area, and volume change is area times distance, we get:

[latex]W = Fd = PA \cdot d = P \Delta V[/latex]

In this form, a positive [latex]\Delta V[/latex] indicates work done by the system on the environment. On a PV diagram, this corresponds to the area under the curve.

The graph of pressure verses volume is shown for a constant pressure. The pressure P is along the Y axis and the volume is along the X axis. The graph is a straight line parallel to the X axis for a value of pressure P. Two points are marked on the graph at either end of the line as A and B. A is the starting point of the graph and B is the end point of graph. There is an arrow pointing from A to B. The term isobaric is written on the graph. For a length of graph equal to delta V the area of the graph is shown as a shaded area given by P times delta V which is equal to work W.
Figure 109.5 On a [latex]PV[/latex] diagram, the work done during an isobaric process, such as the one shown in Figure 109.4, is the area under the curve: [latex]W = P \Delta V[/latex].

General PV Processes

When both pressure and volume vary, the work is still the area under the curve on a [latex]PV[/latex] diagram. The process may be divided into small intervals:

[latex]W = \sum P_{\text{ave}} \Delta V[/latex]
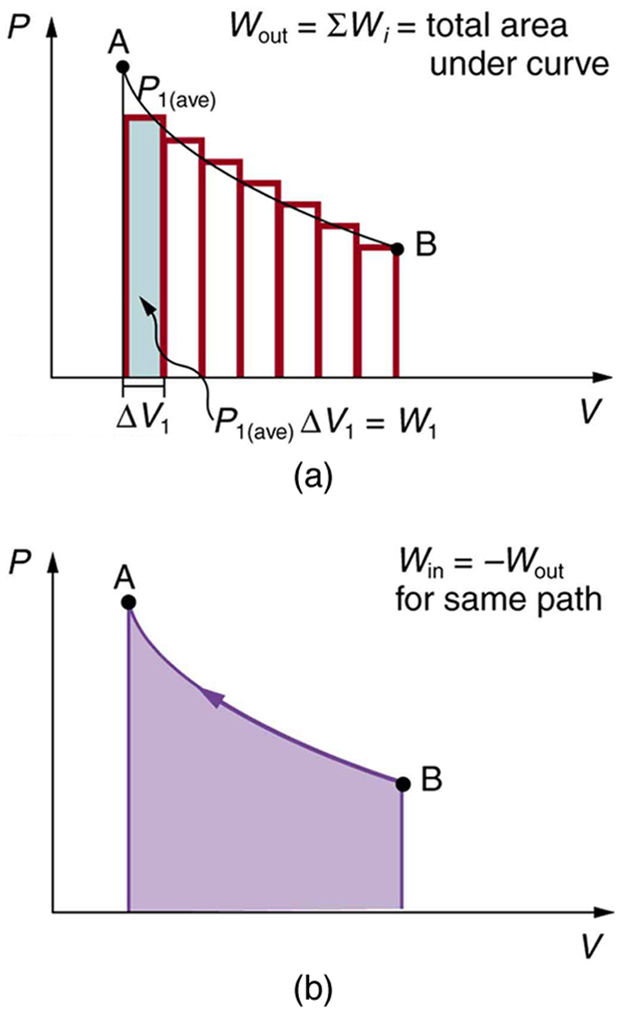
The diagram in part a shows a pressure versus volume graph. The pressure is along the Y axis and the volume is along the X axis. The curve is a smooth falling curve from the highest point A to the lowest point B. The curve is segmented into small vertical rectangular sections of equal width. One of the sections is marked as width of delta V sub one along the X axis. The pressure P sub one average multiplied by delta V sub one gives the work done for that strip of the graph. Part b of the figure shows a similar graph for the reverse path. The curve now slopes upward from point A to point B. An equation in the top right of the graph reads W sub in equals the opposite of W sub out for the same path.
Figure 109.6 ((a) Work done is approximated as the sum of the areas under pressure-volume segments. (b) Reversing the path implies negative work, shown by a downward-sloping curve.

Cyclic Processes and Net Work

If a gas goes through a cycle and returns to its starting point, the total work done is the area enclosed by the path on a [latex]PV[/latex] diagram. Clockwise loops imply positive work output.

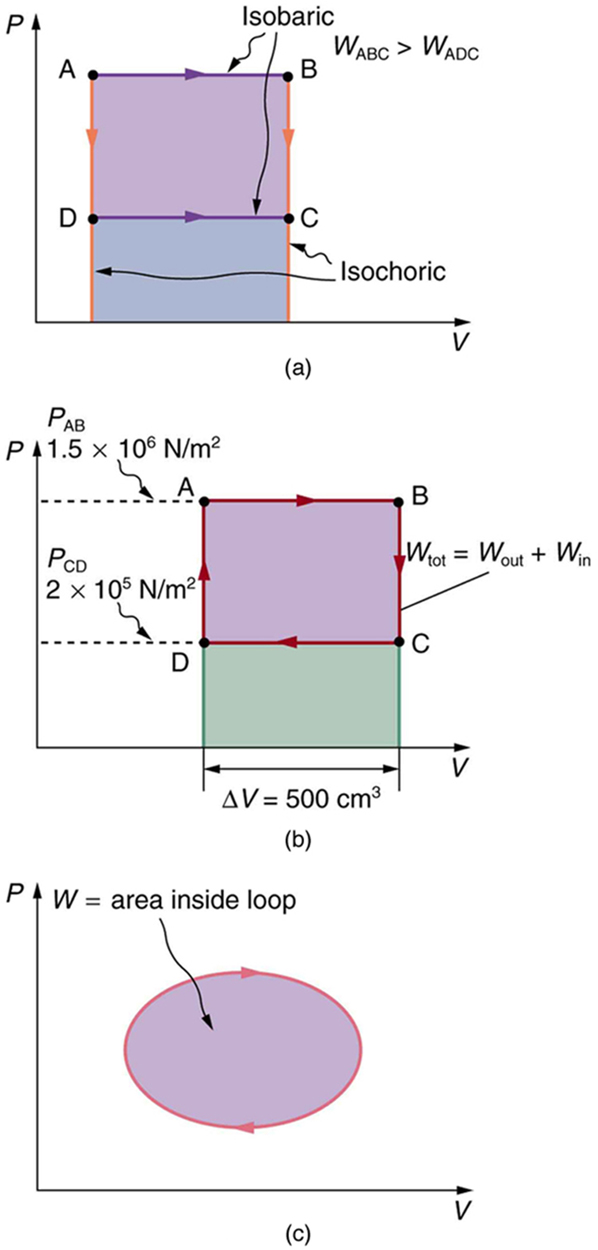
Part a of the diagram shows a pressure versus volume graph. The pressure is along the Y axis and the volume is along the X axis. The curve has a rectangular shape. The curve is labeled A B C D. The paths A B and D C represent isobaric processes as shown by lines pointing toward the right, and A D and B C represent isochoric processes, as shown by lines pointing vertically downward. W sub A B C is shown greater than W sub A D C. The area below the curve A B C D, filling the rectangle A B C D, and the area immediately below path D C are also shaded. Part b of the diagram shows a pressure versus volume graph. The pressure is along the Y axis and the volume is along the X axis. The curve has a rectangular shape and is labeled A B C D. The paths A B and C D represent isobaric processes; A B is a line pointing to the right, and C D is a line pointing to the left. The paths B C and D A represent isochoric processes; B C points vertically downward, and D A points vertically upward. The length of the graph along A B is marked as delta V equals five hundred centimeters cubed. The line A B on the graph is shown to have a pressure P sub A B equals one point five multiplied by ten to the power six Newtons per meter square. The line D on the graph is shown to have a pressure P sub C D equals one point two multiplied by ten to the power five Newtons per meter squared. The total work is marked as W sub tot equals W sub out plus W sub in. Part c of the diagram shows a pressure versus volume graph. The pressure is along the Y axis and the volume is along the X axis. The graph is a closed loop in the form of an ellipse with the arrow pointing in clockwise direction. The shaded area inside the ellipse represents the work done.
Figure 109.7 (a) Work depends on the specific path taken between two states. (b) In a rectangular cycle, net work equals the enclosed area. (c) In any closed loop, the direction determines the sign of the work done.

Example 109.1 Total Work Done in a Cyclical Process Equals the Area Inside the Closed Loop on a PV Diagram

Calculate the total work done in the cyclical process ABCDA shown in Figure 109.7  by the following two methods to verify that work equals the area inside the closed loop on the [latex]\text{PV}[/latex] diagram. (Take the data in the figure to be precise to three significant figures.) (a) Calculate the work done along each segment of the path and add these values to get the total work. (b) Calculate the area inside the rectangle ABCDA.

Strategy

To find the work along any path on a [latex]\text{PV}[/latex] diagram, you use the fact that work is pressure times change in volume, or [latex]W=P\Delta V[/latex]. So in part (a), this value is calculated for each leg of the path around the closed loop.

Solution for (a)

The work along path AB is

[latex]\begin{array}{lll}{W}_{\text{AB}}& =& {P}_{\text{AB}}\Delta {V}_{\text{AB}}\\ & =& \left(1\text{.}\text{50}×{\text{10}}^{6}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}\right)\left(5\text{.}\text{00}×{\text{10}}^{–4}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{3}\right)=\text{750}\phantom{\rule{0.25em}{0ex}}\text{J.}\end{array}[/latex]

Since the path BC is isochoric, [latex]\Delta {V}_{\text{BC}}=0[/latex], and so [latex]{W}_{\text{BC}}=0[/latex]. The work along path CD is negative, since [latex]\Delta {V}_{\text{CD}}[/latex] is negative (the volume decreases). The work is

[latex]\begin{array}{lll}{W}_{\text{CD}}& =& {P}_{\text{CD}}\Delta {V}_{\text{CD}}\\ & =& \left(2\text{.}\text{00}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}\right)\left(–5\text{.}\text{00}×{\text{10}}^{–4}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{3}\right)\phantom{\rule{0.25em}{0ex}}\text{=}\phantom{\rule{0.25em}{0ex}}\text{–}\text{100}\phantom{\rule{0.25em}{0ex}}\text{J}\text{.}\end{array}[/latex]

Again, since the path DA is isochoric, [latex]\Delta {V}_{\text{DA}}=0[/latex], and so [latex]{W}_{\text{DA}}=0[/latex]. Now the total work is

[latex]\begin{array}{lll}W& =& {W}_{\text{AB}}+{W}_{\text{BC}}+{W}_{\text{CD}}+{W}_{\text{DA}}\\ & =& \text{750 J}+0+\left(-\text{100}\text{J}\right)+0=\text{650 J.}\end{array}[/latex]

Solution for (b)

The area inside the rectangle is its height times its width, or

[latex]\begin{array}{lll}\text{area}& =& \left({P}_{\text{AB}}-{P}_{\text{CD}}\right)\Delta V\\ & =& \left[\left(\text{1.50}×{\text{10}}^{6}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}\right)-\left(2\text{.}\text{00}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}\right)\right]\left(5\text{.}\text{00}×{\text{10}}^{-4}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{3}\right)\\ & =& \text{650 J.}\end{array}[/latex]

Thus,

[latex]\text{area}=\text{650}\phantom{\rule{0.25em}{0ex}}\text{J}=W\text{.}[/latex]

Discussion

The result, as anticipated, is that the area inside the closed loop equals the work done. The area is often easier to calculate than is the work done along each path. It is also convenient to visualize the area inside different curves on [latex]\text{PV}[/latex] diagrams in order to see which processes might produce the most work. Recall that work can be done to the system, or by the system, depending on the sign of [latex]W[/latex]. A positive [latex]W[/latex] is work that is done by the system on the outside environment; a negative [latex]W[/latex] represents work done by the environment on the system.

Figure 109.8(a) shows two other important processes on a [latex]\text{PV}[/latex] diagram. For comparison, both are shown starting from the same point A. The upper curve ending at point B is an isothermal process—that is, one in which temperature is kept constant. If the gas behaves like an ideal gas, as is often the case, and if no phase change occurs, then [latex]\text{PV}=\text{nRT}[/latex]. Since [latex]T[/latex] is constant, [latex]\text{PV}[/latex] is a constant for an isothermal process. We ordinarily expect the temperature of a gas to decrease as it expands, and so we correctly suspect that heat transfer must occur from the surroundings to the gas to keep the temperature constant during an isothermal expansion. To show this more rigorously for the special case of a monatomic ideal gas, we note that the average kinetic energy of an atom in such a gas is given by

[latex]\frac{1}{2}m{\overline{v}}^{2}=\frac{3}{2}\text{kT}\text{.}[/latex]

The kinetic energy of the atoms in a monatomic ideal gas is its only form of internal energy, and so its total internal energy [latex]U[/latex] is

[latex]U=N\frac{1}{2}m{\overline{v}}^{2}=\frac{3}{2}\text{NkT},\text{ (monatomic ideal gas),}[/latex]

where [latex]N[/latex] is the number of atoms in the gas. This relationship means that the internal energy of an ideal monatomic gas is constant during an isothermal process—that is, [latex]\Delta U=0[/latex]. If the internal energy does not change, then the net heat transfer into the gas must equal the net work done by the gas. That is, because [latex]\Delta U=Q-W=0[/latex] here, [latex]Q=W[/latex]. We must have just enough heat transfer to replace the work done. An isothermal process is inherently slow, because heat transfer occurs continuously to keep the gas temperature constant at all times and must be allowed to spread through the gas so that there are no hot or cold regions.

Also shown in Figure 109.8(a) is a curve AC for an adiabatic process, defined to be one in which there is no heat transfer—that is, [latex]Q=0[/latex]. Processes that are nearly adiabatic can be achieved either by using very effective insulation or by performing the process so fast that there is little time for heat transfer. Temperature must decrease during an adiabatic process, since work is done at the expense of internal energy:

[latex]U=\frac{3}{2}\text{NkT}\text{.}[/latex]

(You might have noted that a gas released into atmospheric pressure from a pressurized cylinder is substantially colder than the gas in the cylinder.) In fact, because [latex]Q=0, \Delta U=–W[/latex] for an adiabatic process. Lower temperature results in lower pressure along the way, so that curve AC is lower than curve AB, and less work is done. If the path ABCA could be followed by cooling the gas from B to C at constant volume (isochorically), Figure 109.8(b), there would be a net work output.

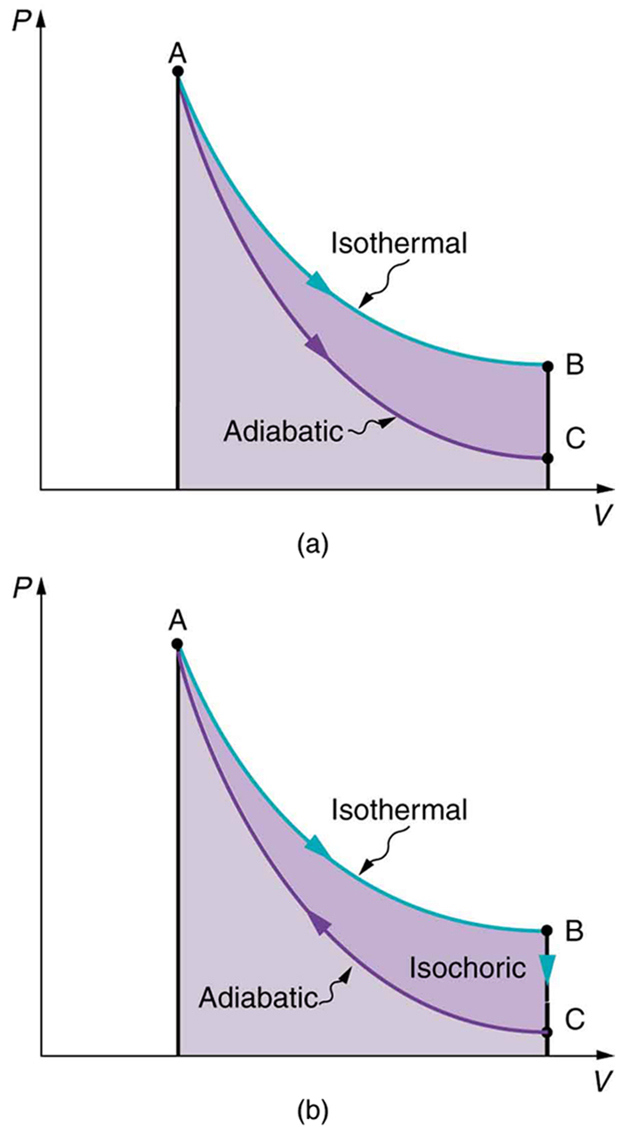
Part a of the figure shows a graph for pressure versus volume. The pressure is along the y axis and the volume is along the x axis. There are two curves. The first curve begins at point A and falls smoothly downward to point B. The graph is shown for an isothermal process. The second curve also begins at point A but falls below the first curve and ends at point C vertically below point B. This graph is shown for an adiabatic process. A line joins point B and C to meet on the X axis. Also a line is drawn from point A to meet the X axis. The area under both the curves is shaded. The graph in figure b is similar to the graph in figure a. Only the directions of the curves are changed. The graph begins from A and moves downward to point B. Then from point B the curve drops vertically downward to C. From point C the graph has a smooth rise back to point A. All directions represented using arrows.
Figure 109.8 (a) The upper curve is an isothermal process ([latex]\text{Δ}T=0[/latex]), whereas the lower curve is an adiabatic process ([latex]Q=0[/latex]). Both start from the same point A, but the isothermal process does more work than the adiabatic because heat transfer into the gas takes place to keep its temperature constant. This keeps the pressure higher all along the isothermal path than along the adiabatic path, producing more work. The adiabatic path thus ends up with a lower pressure and temperature at point C, even though the final volume is the same as for the isothermal process. (b) The cycle ABCA produces a net work output.

Reversible Processes

Certain thermodynamic processes, such as isothermal and adiabatic processes (see Figure 109.8), are considered reversible—at least in theory. A reversible process is one in which both the thermodynamic system and its surroundings can be returned precisely to their original states by following the reverse path.

In the example of a gas in a piston-cylinder system (similar to Figure 109.4), the reverse isothermal and adiabatic paths would be labeled BA and CA, respectively, on a PV diagram. For reversibility to hold, every aspect of the system and its environment must be perfectly restored.

However, real-world macroscopic processes are never exactly reversible. Energy dissipation—due to friction, turbulence, or imperfect insulation—leads to heat transfer in both directions, regardless of the direction of motion. For instance, even if the gas returns to its initial thermodynamic state, the environment may not, due to accumulated energy losses. Reversibility would require the direction of heat flow to reverse as well, which is not possible in practice.

This highlights a fundamental limitation in real systems: perfectly reversible processes do not occur in nature. The underlying reason is the presence of dissipative mechanisms and the constraints imposed by the second law of thermodynamics. While the first law of thermodynamics does not prevent reverse heat flow (e.g., from cold to hot), we observe that such spontaneous processes never occur. The bursting of a bubble or mixing of substances are everyday examples of irreversible processes.

These observations lead us to the necessity of a second thermodynamic principle, one that defines the direction of processes and limits the efficiency of heat engines. As we’ll see, even idealized, perfectly efficient heat engines must operate through reversible processes to reach their maximum theoretical efficiency. Yet, even these ideal engines cannot convert all thermal energy into useful work.

Summary of Common Thermodynamic Processes

The table below summarizes the major simple thermodynamic processes used in heat engines, along with their defining characteristics and equations:

Table 109.1 Summary of Simple Thermodynamic Processes
Isobaric Constant pressure [latex]W=P\Delta V[/latex]
Isochoric Constant volume [latex]W=0[/latex]
Isothermal Constant temperature [latex]Q=W[/latex]
Adiabatic No heat transfer [latex]Q=0[/latex]

PhET Explorations: States of Matter

Use the interactive PhET simulation below to observe how different types of molecules behave in solids, liquids, and gases. You can:

  • Add or remove thermal energy to trigger phase changes.
  • Adjust the temperature or volume of a container and observe changes in pressure.
  • View a real-time pressure–temperature (P–T) diagram and relate macroscopic thermodynamic behavior to microscopic particle motion.
  • Explore how intermolecular forces and interaction potentials affect state changes and particle motion.

Section Summary

  • A heat engine is a machine that uses heat transfer to perform work, following the first law of thermodynamics.
  • Key thermodynamic processes include isobaric (constant pressure), isochoric (constant volume), isothermal (constant temperature), and adiabatic (no heat transfer).
  • Each process influences pressure, volume, temperature, and energy transfer differently.
  • The sign of the work [latex]W[/latex] depends on the direction: if work is done by the system on the environment, [latex]W[/latex] is positive; if work is done on the system, [latex]W[/latex] is negative.
  • Although isothermal and adiabatic processes can be theoretically reversible, real systems always involve some energy dissipation, making perfect reversibility impossible in practice.

Conceptual Questions

  1. A great deal of effort, time, and money has been spent in the quest for the so-called perpetual-motion machine, which is defined as a hypothetical machine that operates or produces useful work indefinitely and/or a hypothetical machine that produces more work or energy than it consumes. Explain, in terms of heat engines and the first law of thermodynamics, why or why not such a machine is likely to be constructed.
  2. One method of converting heat transfer into doing work is for heat transfer into a gas to take place, which expands, doing work on a piston, as shown in the figure below. (a) Is the heat transfer converted directly to work in an isobaric process, or does it go through another form first? Explain your answer. (b) What about in an isothermal process? (c) What about in an adiabatic process (where heat transfer occurred prior to the adiabatic process)?
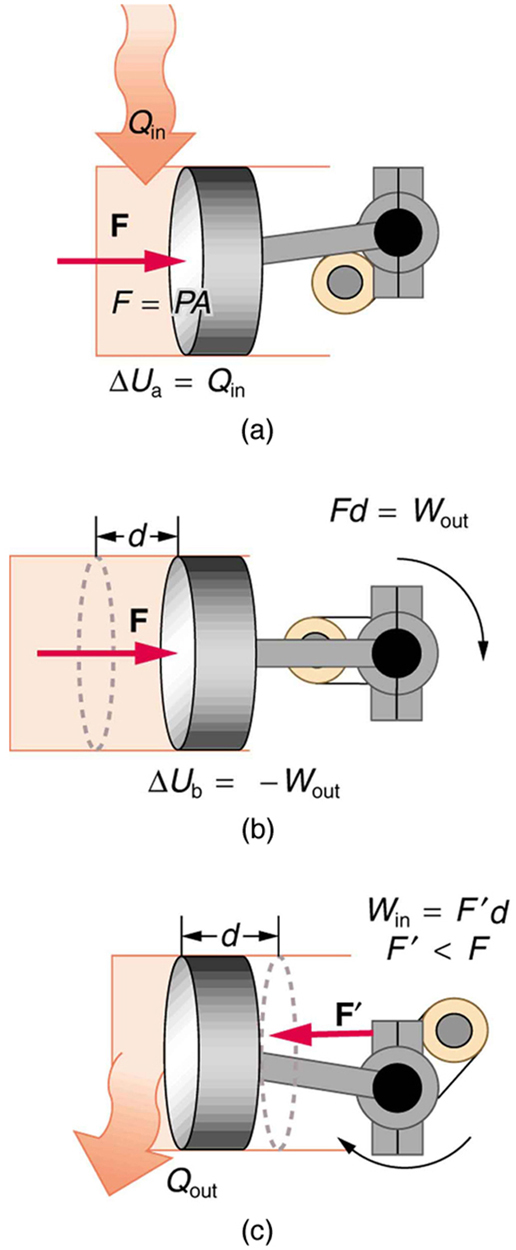
    Figure a shows a piston attached to a movable cylinder which is attached to the right of another gas filled cylinder. The heat Q sub in is shown to be transferred to the gas in the cylinder as shown by a bold arrow toward it. The force of the gas on the moving cylinder with the piston is shown as F equals P times A shown as a vector arrow pointing toward the right. The change in internal energy is marked in the diagram as delta U sub a equals Q sub in. Figure b shows a piston attached to a movable cylinder which is attached to the right of another gas filled cylinder. The force of the gas has moved the cylinder with the piston by a distance d toward the right. The change in internal energy is marked in the diagram as delta U sub b equals negative W sub out. The piston is shown to have done work by change in position, marked as F d equal to W sub out. Figure c shows a piston attached to a movable cylinder which is attached to the right of another gas filled cylinder. The piston attached to the cylinder is shown to reach back to the initial position shown in figure a. The distance d is traveled back and heat Q sub out is shown to leave the system as represented by an outward arrow. The force driving backward is shown as a vector arrow pointing to the left, labeled F prime. F prime is shown less than F. The work done by the force F prime is shown by the equation W sub in equal to F prime times d.
    Figure 109.9
  3. Would the previous question make any sense for an isochoric process? Explain your answer.
  4. We ordinarily say that [latex]\Delta U=0[/latex] for an isothermal process. Does this assume no phase change takes place? Explain your answer.
  5. The temperature of a rapidly expanding gas decreases. Explain why in terms of the first law of thermodynamics. (Hint: Consider whether the gas does work and whether heat transfer occurs rapidly into the gas through conduction.)
  6. Which cyclical process represented by the two closed loops, ABCFA and ABDEA, on the [latex]\text{PV}[/latex] diagram in the figure below produces the greatest net work? Is that process also the one with the smallest work input required to return it to point A? Explain your responses.
  7. The two cyclical processes shown on this [latex]\mathrm{PV}[/latex] diagram start with and return the system to the conditions at point A, but they follow different paths and produce different amounts of work.
    The figure shows a graph of pressure versus volume. The pressure is along the Y axis and the volume is plotted along the X axis. The graph consists of a rectangle, A B C F, superimposed on a slightly larger rectangle, A B D E. The lines A B, C F, and D E are parallel to the X axis and lines B C D and A F E are parallel to the Y axis.
    Figure 109.10
  8. A real process may be nearly adiabatic if it occurs over a very short time. How does the short time span help the process to be adiabatic?
  9. It is unlikely that a process can be isothermal unless it is a very slow process. Explain why. Is the same true for isobaric and isochoric processes? Explain your answer.

Problem Exercises

  1. A car tire contains [latex]0\text{.}\text{0380}{m}^{3}[/latex] of air at a pressure of [latex]2\text{.}\text{20}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}[/latex] (about 32 psi). How much more internal energy does this gas have than the same volume has at zero gauge pressure (which is equivalent to normal atmospheric pressure)?
  2. A helium-filled toy balloon has a gauge pressure of 0.200 atm and a volume of 10.0 L. How much greater is the internal energy of the helium in the balloon than it would be at zero gauge pressure?
  3. Steam to drive an old-fashioned steam locomotive is supplied at a constant gauge pressure of [latex]1\text{.}\text{75}×{\text{10}}^{6}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}[/latex] (about 250 psi) to a piston with a 0.200-m radius. (a) By calculating [latex]P\text{Δ}V[/latex], find the work done by the steam when the piston moves 0.800 m. Note that this is the net work output, since gauge pressure is used. (b) Now find the amount of work by calculating the force exerted times the distance traveled. Is the answer the same as in part (a)?
  4. A hand-driven tire pump has a piston with a 2.50-cm diameter and a maximum stroke of 30.0 cm. (a) How much work do you do in one stroke if the average gauge pressure is [latex]2\text{.}\text{40}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}[/latex] (about 35 psi)? (b) What average force do you exert on the piston, neglecting friction and gravitational force?
  5. Calculate the net work output of a heat engine following path ABCDA in the figure below. 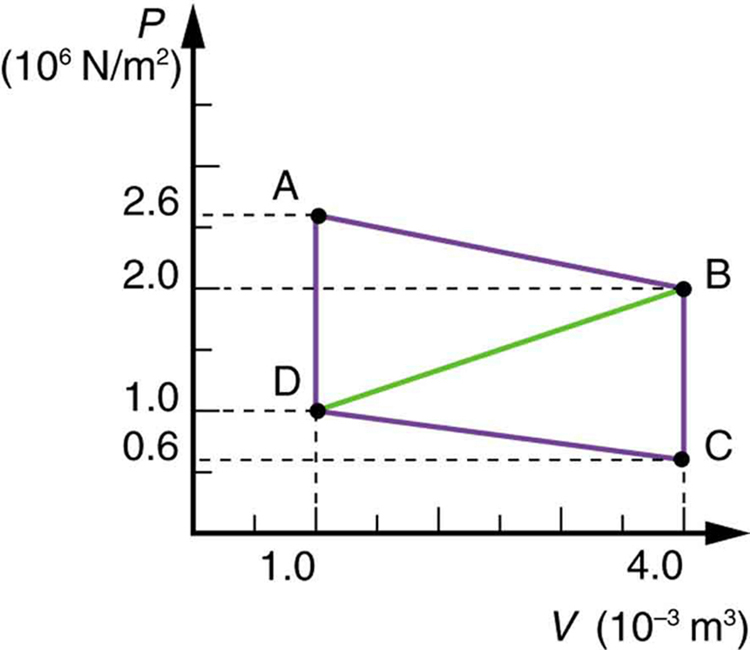A graph is shown of pressure versus volume, with pressure on the Y axis and volume on the X axis. A parallelogram connects four points are on the graph, A, B, C, and D. A is at y equals 2 point 6 times 10 to the six newtons per meter squared and x equals 1 point zero times ten to the minus three meters cubed. A downward sloping line connects A to B. B is at y equals 2 point zero, x equals four. A vertical line connects B to C. C is at y equals zero point 6, x equals 4. A line connects C to D. D is at y equals one point zero, x equals one point zero. A vertical line connects D to A. A diagonal line also connects D and B.Figure 109.11
  6. What is the net work output of a heat engine that follows path ABDA in the figure above, with a straight line from B to D? Why is the work output less than for path ABCDA?
  7. Unreasonable Results What is wrong with the claim that a cyclical heat engine does 4.00 kJ of work on an input of 24.0 kJ of heat transfer while 16.0 kJ of heat transfers to the environment?
  8. (a) A cyclical heat engine, operating between temperatures of [latex]\text{450º C}[/latex] and [latex]\text{150º C}[/latex] produces 4.00 MJ of work on a heat transfer of 5.00 MJ into the engine. How much heat transfer occurs to the environment? (b) What is unreasonable about the engine? (c) Which premise is unreasonable?
  9. Construct Your Own Problem Consider a car’s gasoline engine. Construct a problem in which you calculate the maximum efficiency this engine can have. Among the things to consider are the effective hot and cold reservoir temperatures. Compare your calculated efficiency with the actual efficiency of car engines.
  10. Construct Your Own Problem Consider a car trip into the mountains. Construct a problem in which you calculate the overall efficiency of the car for the trip as a ratio of kinetic and potential energy gained to fuel consumed. Compare this efficiency to the thermodynamic efficiency quoted for gasoline engines and discuss why the thermodynamic efficiency is so much greater. Among the factors to be considered are the gain in altitude and speed, the mass of the car, the distance traveled, and typical fuel economy.

Glossary

heat engine
a machine that uses heat transfer to do work
isobaric process
constant-pressure process in which a gas does work
isochoric process
a constant-volume process
isothermal process
a constant-temperature process
adiabatic process
a process in which no heat transfer takes place
reversible process
a process in which both the heat engine system and the external environment theoretically can be returned to their original states
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book