Thermodynamics
108 The First Law of Thermodynamics
Learning Objectives
- Define the first law of thermodynamics.
- Explain how the law of conservation of energy is expressed in thermodynamics.
- Identify biological and everyday examples that illustrate the first law of thermodynamics.
- Perform calculations involving internal energy, heat transfer, and work.
The first law of thermodynamics is a statement of the principle of energy conservation tailored to systems where energy enters or exits as heat or work. This law is crucial when analyzing how biological or physical systems use heat to perform mechanical tasks.
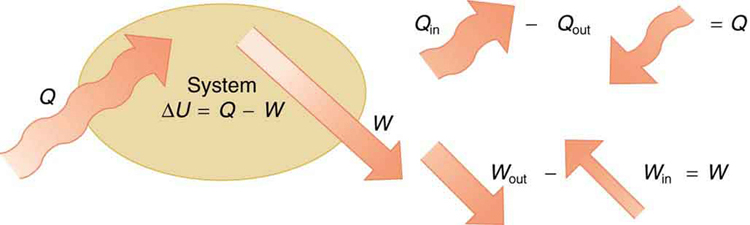
In simple terms, the first law states that the change in a system’s internal energy is equal to the heat added to the system minus the work done by the system:
Here:
- [latex]\Delta U[/latex] is the change in internal energy of the system.
- [latex]Q[/latex] is the net heat transferred into the system (positive when heat is added).
- [latex]W[/latex] is the net work done by the system on the surroundings (positive when work is done by the system).
Consider a heat engine or even a human body as a system. If the heat added to the system exceeds the work done, the excess is stored as internal energy—raising the system's temperature or changing its physical state. Figure 108.1 shows a tea kettle converting heat into work through steam expansion and whistling.
This principle also explains why biological metabolism requires energy intake (in the form of food calories). The body uses this energy to perform work (such as muscle contractions) and maintain internal temperatures.

Understanding the Equation: [latex]\Delta U = Q - W[/latex]
Heat ([latex]Q[/latex]) and work ([latex]W[/latex]) are two different processes through which energy enters or leaves a system. Heat results from a temperature difference and moves in a disorganized way, while work involves organized mechanical action, like pushing a piston or pumping blood.
Despite their differences, both processes can result in similar outcomes—like raising temperature. For instance, inflating a bike tire warms the air inside either through solar heating or by compressing it using a pump.
Neither heat nor work is stored in a system. Only internal energy [latex]U[/latex] can be considered a stored quantity. It includes the sum of all microscopic kinetic and potential energies of molecules in the system.
Microscopic vs. Macroscopic Views of Internal Energy
We can think of internal energy in two ways:
- Microscopic view: The total kinetic and potential energies of all atoms and molecules.
- Macroscopic view: Observable properties like temperature, pressure, and volume that reflect molecular averages.
Internal energy depends only on the system’s state—such as its pressure, volume, and temperature—not on how it reached that state. This means that while [latex]Q[/latex] and [latex]W[/latex] depend on the specific processes used, [latex]\Delta U[/latex] does not. This is why we say that internal energy is a state function. (See Figure 108.2)
Making Connections: Energy Conservation in Thermodynamics
The first law of thermodynamics is the familiar conservation of energy principle adapted to thermal systems. It helps us account for how energy flows in and out through heat and work, while internal energy accounts for the net result.
Making Connections: Macroscopic vs. Microscopic
In biology and health sciences, we often observe macroscopic signs like body temperature, metabolism, or blood pressure. However, the underlying cause of these changes—energy transfers at the molecular level—can be explained by the microscopic view of internal energy. Thermodynamics bridges these two scales.
Example 108.1 Calculating Change in Internal Energy: The Same Change in [latex]U[/latex] is Produced by Two Different Processes
- Suppose there is heat transfer of 40.00 J to a system, while the system does 10.00 J of work. Later, there is heat transfer of 25.00 J out of the system while 4.00 J of work is done on the system. What is the net change in internal energy of the system?
- What is the change in internal energy of a system when a total of 150.00 J of heat transfer occurs out of (from) the system and 159.00 J of work is done on the system? (See Figure 108.3).
Strategy
In part (a), we must first find the net heat transfer and net work done from the given information. Then the first law of thermodynamics [latex]\left(\Delta U=Q-W\right)[/latex] can be used to find the change in internal energy. In part (b), the net heat transfer and work done are given, so the equation can be used directly.
Solution for (a)
The net heat transfer is the heat transfer into the system minus the heat transfer out of the system, or
Similarly, the total work is the work done by the system minus the work done on the system, or
Thus the change in internal energy is given by the first law of thermodynamics:
We can also find the change in internal energy for each of the two steps. First, consider 40.00 J of heat transfer in and 10.00 J of work out, or
Now consider 25.00 J of heat transfer out and 4.00 J of work in, or
The total change is the sum of these two steps, or
Discussion on (a)
No matter whether you look at the overall process or break it into steps, the change in internal energy is the same.
Solution for (b)
Here the net heat transfer and total work are given directly to be [latex]Q=–\text{150}\text{.}\text{00 J}[/latex] and [latex]W=–\text{159}\text{.}\text{00 J}[/latex], so that [latex]\Delta U=Q–W=–\text{150}\text{.}\text{00 J}–\left(-\text{159}\text{.}\text{00 J}\right)=9\text{.}\text{00 J.}[/latex]
Discussion on (b)
A very different process in part (b) produces the same 9.00-J change in internal energy as in part (a). Note that the change in the system in both parts is related to [latex]\Delta U[/latex] and not to the individual [latex]Q[/latex]s or [latex]W[/latex]s involved. The system ends up in the same state in both (a) and (b). Parts (a) and (b) present two different paths for the system to follow between the same starting and ending points, and the change in internal energy for each is the same—it is independent of path.

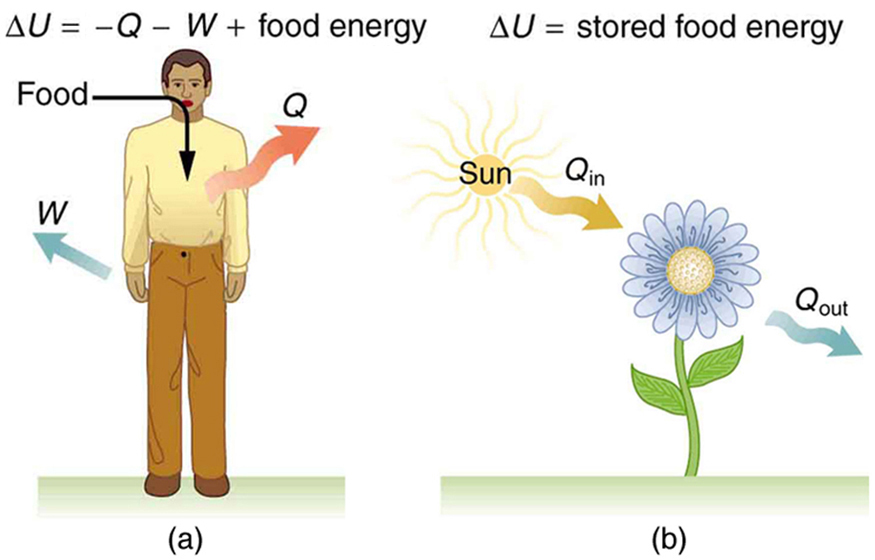
Human Metabolism and the First Law of ThermodynamicsThe metabolism of the human body involves converting chemical energy from food into work, heat, and stored energy—primarily in the form of fat. This process provides a rich example of the first law of thermodynamics in action. By treating the body as a thermodynamic system, we can use the first law to analyze how energy is transferred and transformed during activities ranging from rest to intense physical exercise.
One of the key observations is that body temperature remains relatively constant. This constancy implies that the body continuously releases heat to the environment, meaning [latex]Q[/latex] is negative. At the same time, the body performs work on the surroundings—such as lifting objects or moving limbs—so [latex]W[/latex] is positive. According to the first law:
In this equation, a negative [latex]Q[/latex] and a positive [latex]W[/latex] both contribute to a net loss in internal energy [latex](\Delta U)[/latex], unless replenished through food intake.
Calories and Food Energy
Eating restores the body's internal energy by adding chemical potential energy. From a thermodynamic perspective, food is a form of energy input—functionally equivalent to work done on the body. This energy is commonly measured in Calories. One nutritional Calorie (with an uppercase “C”) is defined as the amount of energy needed to raise the temperature of 1 kilogram of water by 1°C, and it is equivalent to 1 kilocalorie in the scientific context.
When food is metabolized—primarily via oxidation reactions—it releases energy that is either used to do work, transferred as heat, or stored as fat. If energy intake from food equals energy lost to heat and work, the body maintains a constant internal energy, or [latex]\Delta U = 0[/latex]. If intake exceeds energy expenditure, [latex]\Delta U[/latex] becomes positive and fat is stored. Conversely, if intake is less than energy expenditure, [latex]\Delta U[/latex] is negative and the body metabolizes fat to compensate.
Thermodynamics of Dieting
Weight loss occurs when the energy the body expends (through work and heat loss) exceeds what is replaced by food, causing a negative change in internal energy. However, weight regulation is not straightforward. When caloric intake decreases, the body responds by lowering its basal metabolic rate (BMR)—the energy used at rest for essential physiological functions. As a result, the body conserves energy and slows fat loss. Repeated dieting leads to an adaptive reduction in BMR, making subsequent attempts at weight loss more difficult.
Exercise plays a key role in weight management by increasing both the work performed by the body and heat transfer, as well as temporarily raising the BMR. Additionally, human metabolism is relatively inefficient at converting chemical energy into mechanical work, meaning more energy is lost as heat—a helpful factor in calorie expenditure during physical activity.
Irreversibility and Biological Systems
Biological processes such as metabolism and photosynthesis are fundamentally irreversible. This means they occur in one direction only under normal conditions. For example, although stored fat can be metabolized to do work and generate heat, the reverse—using external heat or mechanical work to create body fat—is not possible. You cannot skip lunch by simply sitting in the sun or walking down stairs. Similarly, photosynthesis in plants converts radiant energy into stored chemical energy, but this energy cannot be recovered by shining light on a plant that has already performed photosynthesis.
These processes are governed by the first law of thermodynamics, which tracks energy conservation from start to finish—regardless of the complex biochemical details in between. This law gives us a powerful tool to analyze human physiology and plant biology, as shown in Figure 108.4.
| Term | Definition |
|---|---|
| [latex]U[/latex] | Internal energy—the sum of the kinetic and potential energies of a system’s atoms and molecules. Can be divided into many subcategories, such as thermal and chemical energy. Depends only on the state of a system (such as its [latex]P[/latex], [latex]V[/latex], and [latex]T[/latex]), not on how the energy entered the system. Change in internal energy is path independent. |
| [latex]Q[/latex] | Heat—energy transferred because of a temperature difference. Characterized by random molecular motion. Highly dependent on path. [latex]Q[/latex] entering a system is positive. |
| [latex]W[/latex] | Work—energy transferred by a force moving through a distance. An organized, orderly process. Path dependent. [latex]W[/latex] done by a system (either against an external force or to increase the volume of the system) is positive. |
Section Summary
- The first law of thermodynamics is [latex]\Delta U = Q - W[/latex], where [latex]\Delta U[/latex] is the change in internal energy, [latex]Q[/latex] is net heat transfer, and [latex]W[/latex] is net work done by the system.
- Heat and work are both energy in motion—not stored—while internal energy is a state function that can be stored.
- Internal energy depends only on the system's current state, not on how that state was achieved.
- Biological processes such as metabolism and photosynthesis illustrate the interplay of heat, work, and internal energy and exemplify irreversible thermodynamic processes.
Conceptual Questions
- Describe the photo of the tea kettle at the beginning of this section in terms of heat transfer, work done, and internal energy. How is heat being transferred? What is the work done and what is doing it? How does the kettle maintain its internal energy?
- The first law of thermodynamics and the conservation of energy, as discussed in Conservation of Energy, are clearly related. How do they differ in the types of energy considered?
- Heat transfer [latex]Q[/latex] and work done [latex]W[/latex] are always energy in transit, whereas internal energy [latex]U[/latex] is energy stored in a system. Give an example of each type of energy, and state specifically how it is either in transit or resides in a system.
- How do heat transfer and internal energy differ? In particular, which can be stored as such in a system and which cannot?
- If you run down some stairs and stop, what happens to your kinetic energy and your initial gravitational potential energy?
- Give an explanation of how food energy (calories) can be viewed as molecular potential energy (consistent with the atomic and molecular definition of internal energy).
- Identify the type of energy transferred to your body in each of the following as either internal energy, heat transfer, or doing work: (a) basking in sunlight; (b) eating food; (c) riding an elevator to a higher floor.
Problems & Exercises
- What is the change in internal energy of a car if you put 12.0 gal of gasoline into its tank? The energy content of gasoline is [latex]1\text{.}3×{\text{10}}^{8}\phantom{\rule{0.25em}{0ex}}\text{J/gal}[/latex]. All other factors, such as
- How much heat transfer occurs from a system, if its internal energy decreased by 150 J while it was doing 30.0 J of work?
- A system does [latex]1\text{.}\text{80}×{\text{10}}^{8}\phantom{\rule{0.25em}{0ex}}\text{J}[/latex] of work while [latex]7\text{.}\text{50}×{\text{10}}^{8}\phantom{\rule{0.25em}{0ex}}\text{J}[/latex] of heat transfer occurs to the environment. What is the change in internal energy of the system assuming no other changes (such as in temperature or by the addition of fuel)?
- What is the change in internal energy of a system which does [latex]4\text{.}\text{50}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{J}[/latex] of work while [latex]3\text{.}\text{00}×{\text{10}}^{6}\phantom{\rule{0.25em}{0ex}}\text{J}[/latex] of heat transfer occurs into the system, and [latex]8\text{.}\text{00}×{\text{10}}^{6}\phantom{\rule{0.25em}{0ex}}\text{J}[/latex] of heat transfer occurs to the environment?
- Suppose a woman does 500 J of work and 9500 J of heat transfer occurs into the environment in the process. (a) What is the decrease in her internal energy, assuming no change in temperature or consumption of food? (That is, there is no other energy transfer.) (b) What is her efficiency?
- (a) How much food energy will a man metabolize in the process of doing 35.0 kJ of work with an efficiency of 5.00%? (b) How much heat transfer occurs to the environment to keep his temperature constant?
- (a) What is the average metabolic rate in watts of a man who metabolizes 10,500 kJ of food energy in one day? (b) What is the maximum amount of work in joules he can do without breaking down fat, assuming a maximum efficiency of 20.0%? (c) Compare his work output with the daily output of a 187-W (0.250-horsepower) motor.
- (a) How long will the energy in a 1470-kJ (350-kcal) cup of yogurt last in a woman doing work at the rate of 150 W with an efficiency of 20.0% (such as in leisurely climbing stairs)? (b) Does the time found in part (a) imply that it is easy to consume more food energy than you can reasonably expect to work off with exercise?
- (a) A woman climbing the Washington Monument metabolizes [latex]6\text{.}\text{00}×{\text{10}}^{2}\phantom{\rule{0.25em}{0ex}}\text{kJ}[/latex] of food energy. If her efficiency is 18.0%, how much heat transfer occurs to the environment to keep her temperature constant? (b) Discuss the amount of heat transfer found in (a). Is it consistent with the fact that you quickly warm up when exercising?
Glossary
- first law of thermodynamics
- states that the change in internal energy of a system equals the net heat transfer into the system minus the net work done by the system
- internal energy
- the sum of the kinetic and potential energies of a system’s atoms and molecules
- human metabolism
- conversion of food into heat transfer, work, and stored fat
states that the change in internal energy of a system equals the net heat transfer into the system minus the net work done by the system
the spontaneous transfer of energy due to a temperature difference
the transfer of energy by a force that causes an object to be displaced; the product of the component of the force in the direction of the displacement and the magnitude of the displacement
the sum of the kinetic and potential energies of a system’s atoms and molecules
a machine that uses heat transfer to do work
conversion of food into heat transfer, work, and stored fat
[latex]\phantom{\rule{0.25em}{0ex}}1\phantom{\rule{0.25em}{0ex}}\text{kilocalorie}\phantom{\rule{0.25em}{0ex}}\text{=}\phantom{\rule{0.25em}{0ex}}\text{1000}\phantom{\rule{0.25em}{0ex}}\text{calories}[/latex]
the total energy conversion rate of a person at rest

