This means that all external forces cancel out. Since forces are vector quantities, this condition must be satisfied along each axis of motion. For systems in two dimensions, this requires:

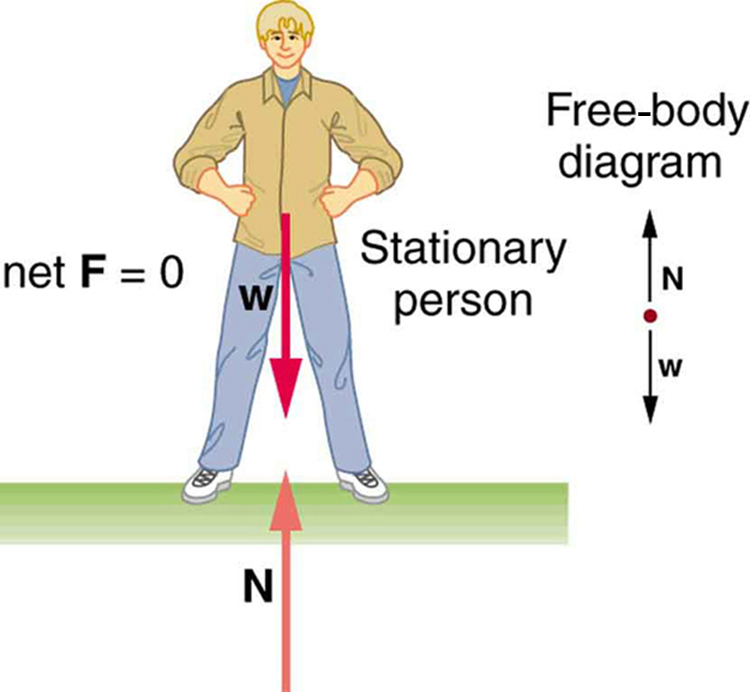
Consider Figure 60.1, which shows a person standing still. The upward normal force from the ground exactly balances the downward gravitational force (weight), so the net force is zero. The person is in static equilibrium, meaning there is no motion and no acceleration.

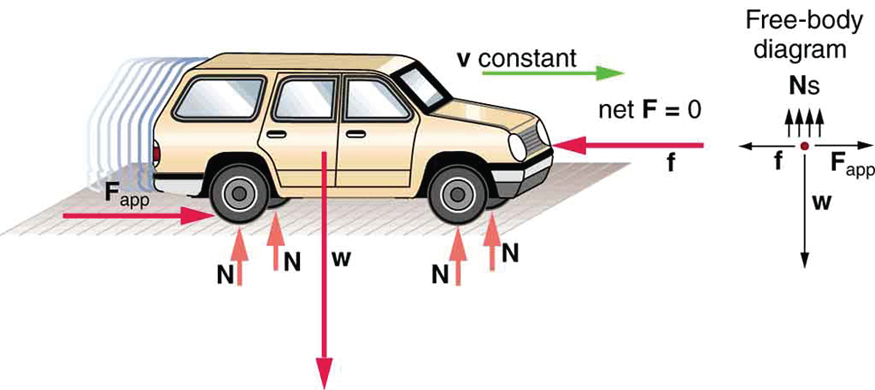
Now consider Figure 60.2. A car moving at constant velocity has balanced horizontal and vertical forces. The horizontal applied force is balanced by air resistance (a form of friction), and the vertical weight is balanced by the normal forces from the road. This is an example of dynamic equilibrium: the object moves but does not accelerate.

It’s important to note that having zero net force does not necessarily mean there is no motion. It simply means there is no change in motion—no acceleration. However, for a system to be truly in equilibrium, force balance alone is not sufficient. The location where a force is applied also matters, especially when considering rotational effects.

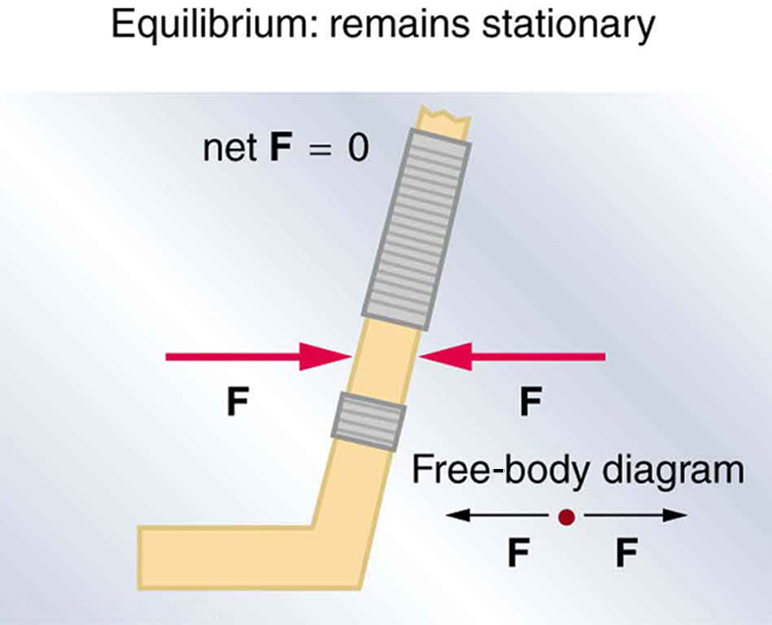
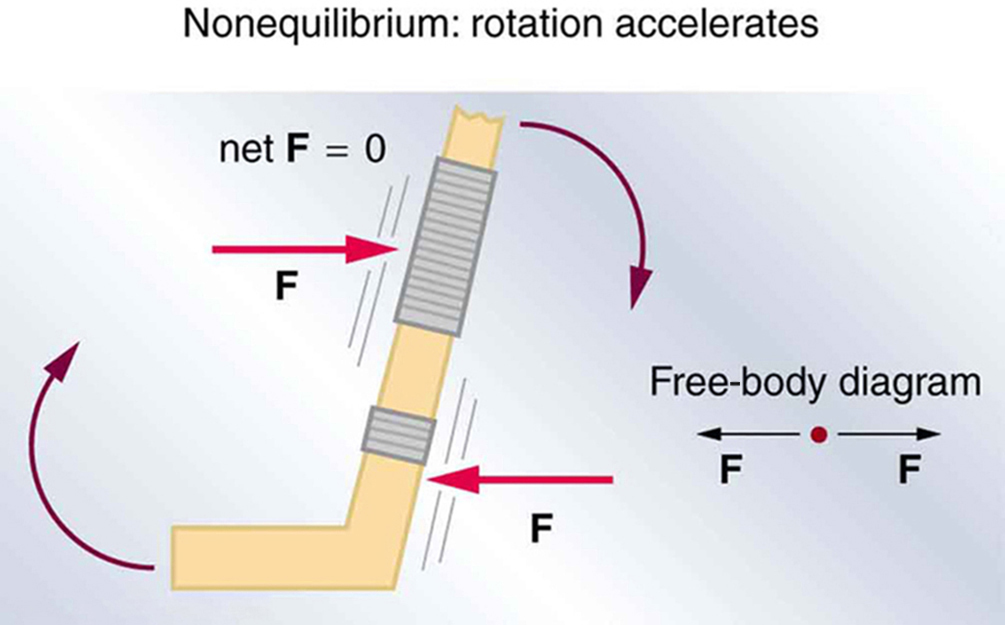
Take a look at Figure 60.3 and Figure 60.4. In both cases, two equal and opposite forces act on a hockey stick. In Figure 60.3, the forces act along the same line of action, so the stick stays still—this is true equilibrium. But in Figure 60.4, the same forces act at different locations, producing a torque that causes the stick to rotate. Even though [latex]\text{net}\,\vec{F} = 0[/latex], the system is not in equilibrium because it experiences angular acceleration. We’ll return to this in the next section.