Oscillatory Motion, Waves, and the Physics of Hearing

125 Superposition and Interference

Learning Objectives

  • Explain how superposition leads to standing waves and beats.
  • Describe the mathematical basis for overtones and beat frequency.
Water surface of a river is shown, with mountains in the background. There are small ripples over the water surface.
Figure 125.1: These waves result from the superposition of several waves from different sources, producing a complex pattern. (credit: waterborough, Wikimedia Commons)

Waves in nature often appear much more complex than simple sinusoidal shapes. As shown in Figure 125.1, most waveforms result from the combination—or superposition—of many individual waves. Despite their complexity, these waves follow straightforward rules. When two or more waves meet at a point in space, their displacements add algebraically. For waves that overlap exactly in phase, their amplitudes combine to produce constructive interference. An example is shown in Figure 125.2, where two identical waves align crest-to-crest and trough-to-trough, resulting in a wave with twice the amplitude.

The graph shows two identical waves that arrive at the same point exactly in phase. The crests of the two waves are precisely aligned, as are the troughs. The amplitude of each wave being X . It produces pure constructive wave. The disturbances add resulting in a new wave with twice the amplitude of the individual waves that is two X but of same wavelength.
Figure 125.2: Constructive interference occurs when two identical waves superimpose in phase, doubling the amplitude.

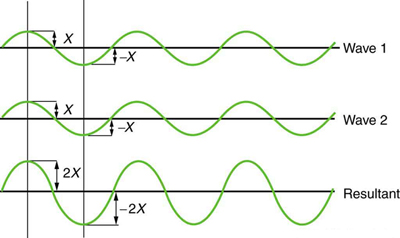
In contrast, Figure 125.3 shows destructive interference, where the crest of one wave aligns with the trough of another. Their displacements cancel out, producing zero net amplitude.

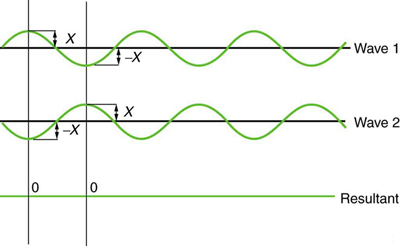
The graph shows two identical waves that arrive exactly out of phase. The crests of one wave are aligned with the trough of another wave. Each wave has amplitude equal to X. As the disturbances are in the opposite directions, they cancel out each other, resulting in zero amplitude which is shown as the third figure showing a green straight line, that is, the waves cancel each other producing pure destructive interference.
Figure 125.3: Destructive interference results when two identical waves overlap out of phase, canceling each other completely.

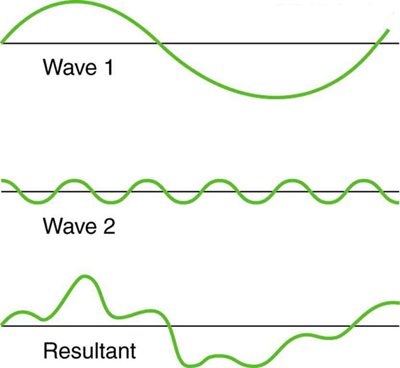
Most wave interactions involve partial alignment, producing a mix of constructive and destructive interference across different locations or times. For example, in a room with multiple audio speakers, certain regions may sound louder due to constructive interference, while others sound muted due to destructive interference. When waves of different shapes and frequencies combine, the resulting waveform becomes more irregular, as shown in Figure 125.4.

The graph shows two non-identical waves with different frequencies and wavelengths. In the first graph only one crest and one trough of the wave are seen. In the second figure five crests are seen in the same length. When they superimpose, the disturbance add and subtract, producing a more complicated looking wave with highly irregular amplitude and wavelength due to combined effect of constructive and destructive interference.
Figure 125.4: Superposition of non-identical waves leads to complex patterns involving both constructive and destructive interference.

Standing Waves

Sometimes waves appear stationary even though they result from moving disturbances. These are called standing waves, created by the superposition of two identical waves traveling in opposite directions. A familiar example is the vibration of fluid surfaces in a container, such as milk in a refrigerator. Standing waves also occur in strings, like those on musical instruments.

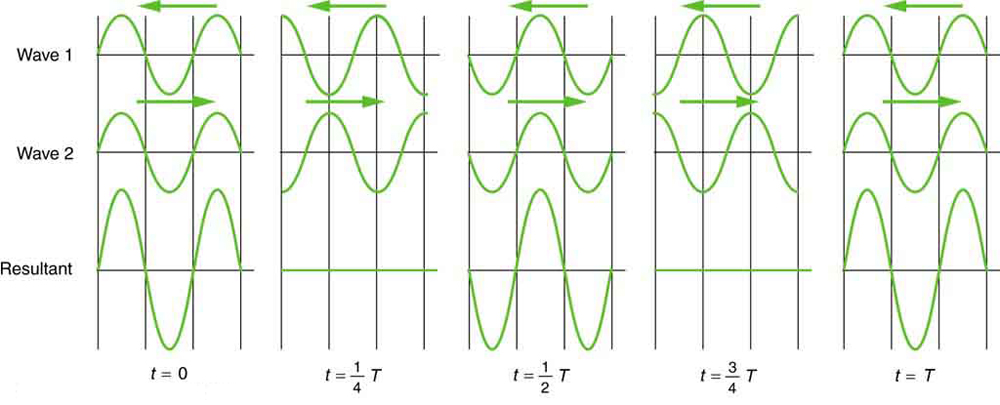
Standing wave combinations of two waves is shown. At the time t is equal to zero. The waves are in the same phase so the amplitude of the superimposed wave is double that of wave one and two. In the second figure at time t is equal to one fourth of time period T , the waves are in opposite phase so their super imposed figure is a straight line. Again at the time t is equal to half the time period the waves are in the same phase and the process is repeated at t is equal to three fourth of time period and at the end of the time period T.
Figure 125.5: Standing wave formed from two waves of equal amplitude traveling in opposite directions. The pattern oscillates in place due to alternating constructive and destructive interference.

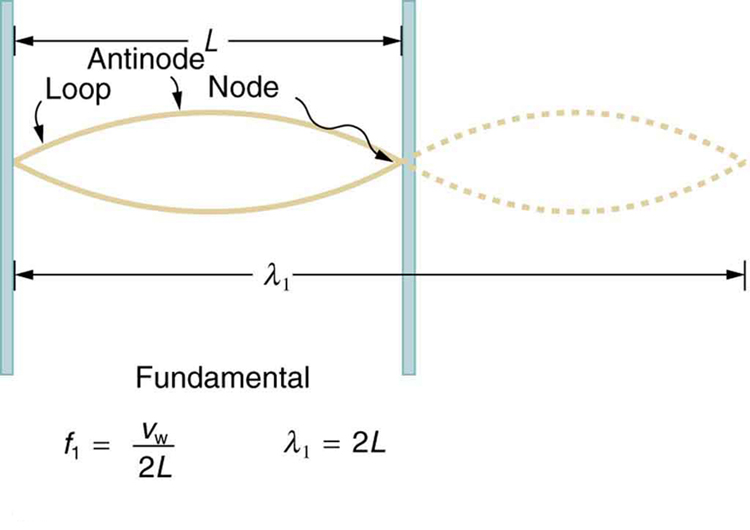
In standing waves, fixed points called nodes remain stationary, while the points of maximum motion are known as antinodes. Strings fixed at both ends form standing waves with quantized frequencies. The fundamental, or lowest frequency, corresponds to the longest wavelength:

[latex]\lambda_1 = 2L[/latex]
[latex]f_1 = \frac{v_{\text{w}}}{\lambda_1} = \frac{v_{\text{w}}}{2L}[/latex]

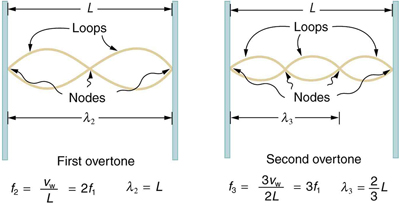
Higher-frequency modes are called harmonics or overtones. The second harmonic (first overtone) has half the wavelength of the fundamental:

[latex]\lambda_2 = L \quad \Rightarrow \quad f_2 = \frac{v_{\text{w}}}{L} = 2f_1[/latex]

And the third harmonic:

[latex]f_3 = 3f_1[/latex]
The graph shows a wave with wavelength lambda one equal to L, which has two loops. There three nodes and two antinodes in the figure. The length of one loop is L.
Figure 125.6: A string oscillating in its fundamental mode with two nodes and one antinode.
first overtone is shown as the wave length if lambda two is L and there are three nodes and two antinodes in the figure. For first overtone the frequency f two is equal to two times f one.
Figure 125.7: Standing waves showing the first and second overtones (harmonics), with increasing numbers of nodes and antinodes.

Beats

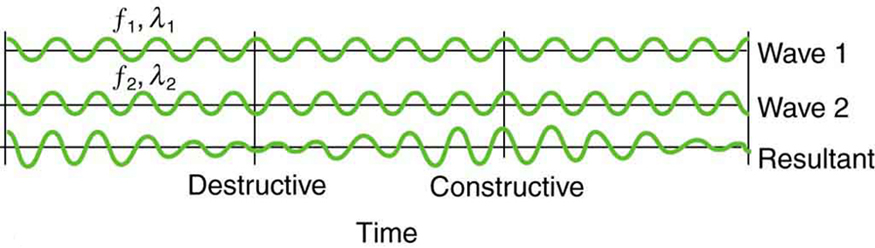
When two sound waves of similar frequency are combined, the result is a wave whose amplitude varies periodically. This phenomenon is known as a beat. Listeners perceive the volume fluctuating—an effect often heard when tuning musical instruments or listening to two closely pitched jet engines.

The graph shows the superimposition of two similar but non-identical waves. Beats are produced by alternating destructive and constructive waves with equal amplitude but different frequencies. The resultant wave is the one with rising and falling amplitude over different intervals of time.
Figure 125.8: Beats arise when two waves with close frequencies interfere, resulting in a time-varying amplitude.

The general form for a wave of frequency [latex]f[/latex] is:

[latex]x = X \cos(2\pi f t)[/latex]

If we add two such waves with frequencies [latex]f_1[/latex] and [latex]f_2[/latex], the result is:

[latex]x = X \cos(2\pi f_1 t) + X \cos(2\pi f_2 t)[/latex]

Using a trigonometric identity:

[latex]x = 2X \cos(\pi f_B t) \cos(2\pi f_{\text{ave}} t)[/latex]

where:

[latex]f_B = |f_1 - f_2| \quad \text{and} \quad f_{\text{ave}} = \frac{f_1 + f_2}{2}[/latex]

The result is a wave with an average frequency and a slowly varying amplitude at the beat frequency [latex]f_B[/latex]. This phenomenon is useful in a range of applications, including sound tuning, radar, and ultrasound imaging.

Making Connections

Piano tuners use beats routinely in their work. When comparing a note with a tuning fork, they listen for beats and adjust the string until the beats fade (to zero frequency). For example, if the tuning fork has a [latex]\text{256}\phantom{\rule{0.25em}{0ex}}\text{Hz}[/latex] frequency and two beats per second are heard, then the other frequency is either [latex]\text{254}[/latex] or [latex]\text{258}\phantom{\rule{0.25em}{0ex}}\text{Hz}[/latex]. Most keys hit multiple strings, and these strings are actually adjusted until they have nearly the same frequency and give a slow beat for richness. Twelve-string guitars and mandolins are also tuned using beats.

While beats may sometimes be annoying in audible sounds, we will find that beats have many applications. Observing beats is a very useful way to compare similar frequencies. There are applications of beats as apparently disparate as in ultrasonic imaging and radar speed traps.

Check Your Understanding

Imagine you are holding one end of a jump rope while your friend holds the other. If your friend holds her end still, you can move your end up and down, creating a transverse wave. If your friend then begins to move her end up and down, generating a wave in the opposite direction, what resultant wave forms would you expect to see in the jump rope?
Answer: The rope would alternate between having waves with amplitudes two times the original amplitude and reaching equilibrium with no amplitude at all. The wavelengths will result in both constructive and destructive interference.
Define nodes and antinodes.
Answer: Nodes are areas of wave interference where there is no motion. Antinodes are areas of wave interference where the motion is at its maximum point.
You hook up a stereo system. When you test the system, you notice that in one corner of the room, the sounds seem dull. In another area, the sounds seem excessively loud. Describe how the sound moving about the room could result in these effects.
Answer: With multiple speakers putting out sounds into the room and these sounds bouncing off the walls, there is bound to be some wave interference. In the dull areas, the interference is probably mostly destructive. In the louder areas, the interference is probably mostly constructive.

Interactive Exploration: Wave Interference

When two or more waves meet, they combine to produce a phenomenon known as interference. Depending on how the waves overlap, they can reinforce one another (constructive interference) or partially or completely cancel one another (destructive interference). In this simulation, you'll explore interference using water waves, sound waves, and light waves, providing a visual demonstration of one of the most fundamental properties of wave motion. Experiment with different wave sources, frequencies, amplitudes, and barriers. Try using a single source, then add a second source or a double slit to observe how interference patterns develop. As you explore, pay attention to the locations where waves consistently reinforce or cancel each other.

Guided Exploration

As you interact with the simulation, try to answer the following questions:

  1. Begin with a single wave source. How do the wavefronts spread as they move away from the source?
  2. Add a second source with the same frequency. Where do you observe constructive interference? Where do you observe destructive interference?
  3. Change the wavelength or frequency of the waves. How does this affect the spacing between the interference fringes?
  4. Switch between water waves, sound waves, and light waves. What similarities and differences do you observe in the interference patterns?
  5. Place a barrier with two narrow openings in the wave path. How does the double-slit arrangement produce an interference pattern beyond the barrier?
  6. Based on your observations, explain why interference provides strong evidence that light, sound, and water disturbances all behave as waves.

After completing the exploration, compare your observations with the concepts presented in this section. Notice that interference occurs because waves obey the principle of superposition; when two or more waves overlap, their displacements add together. This produces regions of constructive interference—where the amplitude increases—and destructive interference—where the amplitude decreases or even becomes zero.

Healthcare Connection

Otoacoustic emissions (OAE) testing, a standard part of newborn hearing screening, relies on the wave phenomena described in this section. A tiny probe placed in the ear canal sends in sound, and the healthy inner ear responds by producing its own faint sound waves as its hair cells vibrate, sound that echoes back out of the ear and can be picked up by a microphone in the probe. These emissions arise in part from the interference and resonance of traveling waves within the fluid-filled cochlea. If the cochlea is damaged, its hair cells generally fail to produce these emissions, so a screening test that detects little or no otoacoustic emission is a strong, quick, noninvasive signal that a newborn may need further hearing evaluation.

Section Summary

  • Superposition is the combination of two waves at the same location.
  • Constructive interference occurs when two identical waves are superimposed in phase.
  • Destructive interference occurs when two identical waves are superimposed exactly out of phase.
  • A standing wave is one in which two waves superimpose to produce a wave that varies in amplitude but does not propagate.
  • Nodes are points of no motion in standing waves.
  • An antinode is the location of maximum amplitude of a standing wave.
  • Waves on a string are resonant standing waves with a fundamental frequency and can occur at higher multiples of the fundamental, called overtones or harmonics.
  • Beats occur when waves of similar frequencies [latex]{f}_{1}[/latex] and [latex]{f}_{2}[/latex] are superimposed. The resulting amplitude oscillates with a beat frequency given by
    [latex]{f}_{\text{B}}=\mid {f}_{1}-{f}_{2}\mid[/latex]

Conceptual Questions

  1. Speakers in stereo systems have two color-coded terminals to indicate how to hook up the wires. If the wires are reversed, the speaker moves in a direction opposite that of a properly connected speaker. Explain why it is important to have both speakers connected the same way.

Problems & Exercises

  1. A car has two horns, one emitting a frequency of 199 Hz and the other emitting a frequency of 203 Hz. What beat frequency do they produce?
  2. The middle-C hammer of a piano hits two strings, producing beats of 1.50 Hz. One of the strings is tuned to 260.00 Hz. What frequencies could the other string have?
  3. Two tuning forks having frequencies of 460 and 464 Hz are struck simultaneously. What average frequency will you hear, and what will the beat frequency be?
  4. Twin jet engines on an airplane are producing an average sound frequency of 4100 Hz with a beat frequency of 0.500 Hz. What are their individual frequencies?
  5. A wave traveling on a Slinky® that is stretched to 4 m takes 2.4 s to travel the length of the Slinky and back again.
    1. What is the speed of the wave?
    2. Using the same Slinky stretched to the same length, a standing wave is created which consists of three antinodes and four nodes. At what frequency must the Slinky be oscillating?
  6. Three adjacent keys on a piano (F, F-sharp, and G) are struck simultaneously, producing frequencies of 349, 370, and 392 Hz. What beat frequencies are produced by this discordant combination?

Glossary

antinode
the location of maximum amplitude in standing waves
beat frequency
the frequency of the amplitude fluctuations of a wave
constructive interference
when two waves arrive at the same point exactly in phase; that is, the crests of the two waves are precisely aligned, as are the troughs
destructive interference
when two identical waves arrive at the same point exactly out of phase; that is, precisely aligned crest to trough
fundamental frequency
the lowest frequency of a periodic waveform
nodes
the points where the string does not move; more generally, nodes are where the wave disturbance is zero in a standing wave
overtones
multiples of the fundamental frequency of a sound
superposition
the phenomenon that occurs when two or more waves arrive at the same point
definition

License

Icon for the Creative Commons Attribution 4.0 International License

Introductory Physics for the Health and Life Sciences I Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book