"

Oscillatory Motion and Waves and Physics of Hearing.

130 Sound Intensity and Sound Level

Learning Objectives

  • Define intensity, sound intensity, and sound pressure level.
  • Calculate sound intensity levels using decibels (dB).
Photograph of a road jammed with traffic of all types of vehicles.
Figure 130.1: Roadway noise, like that seen here in Delhi, can make normal conversation impossible without shouting. (credit: Lingaraj G J, Flickr)

In quiet surroundings, like a forest, you might hear a single leaf drop. In contrast, when near loud traffic, it’s often impossible to hear someone speaking right next to you. We are familiar with these changes in loudness and know they are linked to how strongly a sound source vibrates. This vibration generates a sound wave—a pressure disturbance moving through a medium such as air. The physical quantity describing this energy transfer is called sound intensity.

Intensity refers to the amount of energy a wave carries per unit area per second. It is mathematically defined as:

[latex]I = \frac{P}{A}[/latex]

Here, [latex]I[/latex] is the intensity, [latex]P[/latex] is the power transmitted, and [latex]A[/latex] is the area over which it spreads. The SI unit of intensity is watts per square meter ([latex]\text{W/m}^2[/latex]).

For sound waves, intensity is also related to pressure amplitude, or how much pressure fluctuates in the wave:

[latex]I = \frac{(\Delta p)^2}{2 \rho v_w}[/latex]

In this equation:

  • [latex]\Delta p[/latex] = pressure variation (Pa)
  • [latex]\rho[/latex] = density of the medium (kg/m³)
  • [latex]v_w[/latex] = speed of sound in the medium (m/s)

Larger pressure variations mean stronger compressions and higher intensity. This is why louder sounds are associated with more forceful vibrations.

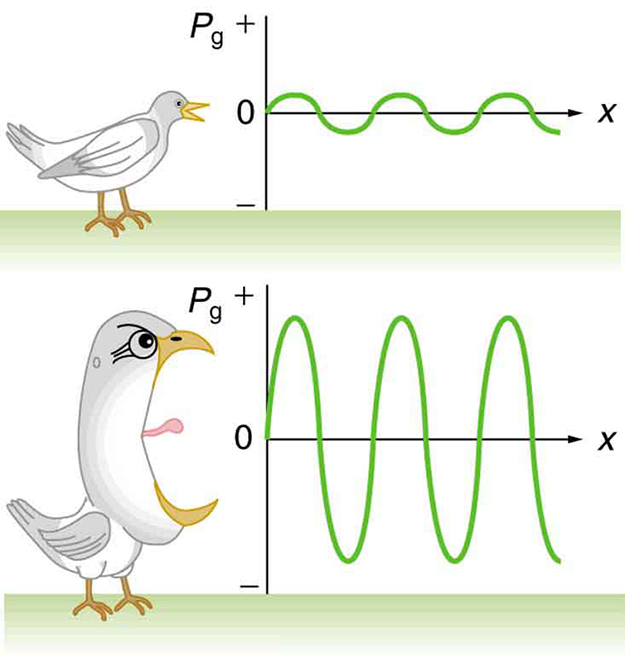
The image shows two graphs, with a bird positioned to the left of each one. The first graph represents a low frequency sound of a bird. The pressure variation shows small amplitude maxima and minima, represented by a sine curve of gauge pressure versus position with a small amplitude. The second graph represents a high frequency sound of a screaming bird. The pressure variation shows large amplitude maxima and minima, represented by a sine curve of gauge pressure versus position with a large amplitude.
Figure 130.2: Pressure vs. position graphs for two sound waves. The high-intensity wave has greater pressure extremes and more energy per unit area.

Sound Intensity Level and Decibels

Sound intensities are commonly expressed in decibels (dB), a logarithmic scale that matches how humans perceive changes in loudness. The sound intensity level [latex]\beta[/latex] in decibels is defined by:

[latex]\beta\ (\text{dB}) = 10 \log_{10}\left(\frac{I}{I_0}\right)[/latex]

Here, [latex]I[/latex] is the intensity of the sound in [latex]\text{W/m}^2[/latex], and [latex]I_0 = 1.0 \times 10^{-12}\ \text{W/m}^2[/latex] is the reference intensity—the threshold of hearing for a typical human at 1000 Hz.

The decibel scale is useful because each factor-of-ten increase in intensity adds 10 dB. For example, a sound that is 10 times more intense than another is 10 dB louder.

Table 130.1: Sound Intensity Levels and Intensities
Sound intensity level β (dB) Intensity I(W/m2) Example/effect
[latex]0[/latex] [latex]1×{10}^{–12}[/latex] Threshold of hearing at 1000 Hz
[latex]10[/latex] [latex]1×{10}^{–11}[/latex] Rustle of leaves
[latex]20[/latex] [latex]1×{10}^{–10}[/latex] Whisper at 1 m distance
[latex]30[/latex] [latex]1×{10}^{–9}[/latex] Quiet home
[latex]40[/latex] [latex]1×{10}^{–8}[/latex] Average home
[latex]50[/latex] [latex]1×{10}^{–7}[/latex] Average office, soft music
[latex]60[/latex] [latex]1×{10}^{–6}[/latex] Normal conversation
[latex]70[/latex] [latex]1×{10}^{–5}[/latex] Noisy office, busy traffic
[latex]80[/latex] [latex]1×{10}^{–4}[/latex] Loud radio, classroom lecture
[latex]90[/latex] [latex]1×{10}^{–3}[/latex] Inside a heavy truck; damage from prolonged exposure1
[latex]100[/latex] [latex]1×{10}^{–2}[/latex] Noisy factory, siren at 30 m; damage from 8 h per day exposure
[latex]110[/latex] [latex]1×{10}^{–1}[/latex] Damage from 30 min per day exposure
[latex]120[/latex] [latex]1[/latex] Loud rock concert, pneumatic chipper at 2 m; threshold of pain
[latex]140[/latex] [latex]1×{10}^{2}[/latex] Jet airplane at 30 m; severe pain, damage in seconds
[latex]160[/latex] [latex]1×{10}^{4}[/latex] Bursting of eardrums

Even very faint sounds involve measurable energy. At the threshold of hearing ([latex]0\ \text{dB}[/latex]), only [latex]10^{-16}[/latex] watts falls on an eardrum of area [latex]1\ \text{cm}^2[/latex]. The range of hearing spans intensities from [latex]10^{-12}[/latex] to [latex]10^0[/latex] [latex]\text{W/m}^2[/latex]—a factor of a trillion!

Comparing Sound Levels

The table below shows how intensity ratios relate to differences in decibel levels:

Table 130.2: Ratios of Intensities and Corresponding Differences in Sound Intensity Levels
[latex]{I}_{2}/{I}_{1}[/latex] [latex]{\beta }_{2}–{\beta }_{1}[/latex]
2.0 3.0 dB
5.0 7.0 dB
10.0 10.0 dB

Because the human ear perceives sound logarithmically, using decibels helps match physical changes in sound with how we actually experience them.

Example 130.1: Calculating Sound Intensity Levels: Sound Waves

Calculate the sound intensity level in decibels for a sound wave traveling in air at [latex]0ºC[/latex]
and having a pressure amplitude of 0.656 Pa.

Strategy

We are given [latex]\Delta p[/latex], so we can calculate [latex]I[/latex] using the equation [latex]I={\left(\Delta p\right)}^{2}/{\left(2{\text{pv}}_{w}\right)}^{2}[/latex]. Using [latex]I[/latex], we can calculate [latex]\beta[/latex] straight from its definition in [latex]\beta \phantom{\rule{0.25em}{0ex}}\left(\text{dB}\right)=\text{10}\phantom{\rule{0.25em}{0ex}}{\text{log}}_{\text{10}}\left(I/{I}_{0}\right)[/latex].

Solution

  1. Identify knowns: Sound travels at 331 m/s in air at [latex]0ºC[/latex].Air has a density of [latex]1.29 kg{/m}^{3}[/latex] at atmospheric pressure and [latex]0ºC[/latex].
  2. Enter these values and the pressure amplitude into
    [latex]I={\left(\Delta p\right)}^{2}/\left({2\text{ρv}}_{w}\right)[/latex]:
    [latex]I=\frac{{\left(\Delta p\right)}^{2}}{2{\text{ρv}}_{w}}=\frac{{\left(0.656 Pa\right)}^{2}}{2\left(1\text{.}\text{29}\phantom{\rule{0.25em}{0ex}}{\text{kg/m}}^{3}\right)\left(\text{331 m/s}\right)}=5\text{.}\text{04}×{\text{10}}^{-4}\phantom{\rule{0.25em}{0ex}}{\text{W/m}}^{2}.[/latex]
  3. Enter the value for [latex]I[/latex] and the known value for [latex]{I}_{0}[/latex] into [latex]\beta \phantom{\rule{0.25em}{0ex}}\left(\text{dB}\right)=\text{10}\phantom{\rule{0.25em}{0ex}}{\text{log}}_{\text{10}}\left(I/{I}_{0}\right)[/latex]. Calculate to find the sound intensity level in decibels:
    [latex]{10 log}_{10}\left(5.04×{10}^{8}\right)=10\phantom{\rule{0.25em}{0ex}}\left(8.70\right)\phantom{\rule{0.25em}{0ex}}dB=87 dB.[/latex]

Discussion

This 87 dB sound has an intensity five times as great as an 80 dB sound. So a factor of five in intensity corresponds to a difference of 7 dB in sound intensity level. This value is true for any intensities differing by a factor of five.

Change Intensity Levels of a Sound: What Happens to the Decibel Level?

Show that if one sound is twice as intense as another, it has a sound level about 3 dB higher.

Strategy

You are given that the ratio of two intensities is 2 to 1, and are then asked to find the difference in their sound levels in decibels. You can solve this problem using of the properties of logarithms.

Solution

  1. Identify knowns:
    The ratio of the two intensities is 2 to 1, or:
    [latex]\frac{{I}_{2}}{{I}_{1}}=2\text{.}\text{00}.[/latex]

    We wish to show that the difference in sound levels is about 3 dB. That is, we want to show:

    [latex]{\beta }_{2}-{\beta }_{1}=3\phantom{\rule{0.25em}{0ex}}\text{dB}.[/latex]

    Note that:

    [latex]{\text{log}}_{\text{10}}b-{\text{log}}_{\text{10}}a={\text{log}}_{\text{10}}\left(\frac{b}{a}\right)\text{.}[/latex]
  2. Use the definition of [latex]\beta[/latex] to get:
    [latex]{\beta }_{2}-{\beta }_{1}={\text{10 log}}_{\text{10}}\left(\frac{{I}_{2}}{{I}_{1}}\right)=\text{10}\phantom{\rule{0.25em}{0ex}}{\text{log}}_{\text{10}}2.00=\text{10}\phantom{\rule{0.25em}{0ex}}\left(0\text{.}\text{301}\right)\phantom{\rule{0.25em}{0ex}}\text{dB}.[/latex]

    Thus,

    [latex]{\beta }_{2}-{\beta }_{1}=3\text{.01 dB}.[/latex]

Discussion

This means that the two sound intensity levels differ by 3.01 dB, or about 3 dB, as advertised. Note that because only the ratio [latex]{I}_{2}/{I}_{1}[/latex] is given (and not the actual intensities), this result is true for any intensities that differ by a factor of two. For example, a 56.0 dB sound is twice as intense as a 53.0 dB sound, a 97.0 dB sound is half as intense as a 100 dB sound, and so on.

There is another decibel-based scale known as the sound pressure level (SPL), which compares the pressure amplitude of a sound wave to a reference pressure. This scale is often used in underwater acoustics (like sonar and marine noise pollution). It differs from the standard sound intensity level discussed in this section. For example, ship-generated ocean noise may be reported as 200 dB SPL, while the equivalent sound intensity level in air would be less than 140 dB. It’s important to note that while both use decibels, they are based on different reference values and are not interchangeable.

Take-Home Investigation: Feeling Sound

Find a music player and a CD with rock music. Place the player on a light table and begin playback. Gently place your hand on the table surface. Slowly increase the volume and observe when the table first begins to vibrate. Then double the volume setting. What do you notice about the intensity of the vibrations?

Check Your Understanding

Describe how amplitude is related to the loudness of a sound.

Loudness is directly related to amplitude. As amplitude increases, the sound becomes louder.

Identify common sounds at the levels of 10 dB, 50 dB, and 100 dB.

  • 10 dB: Running fingers through hair
  • 50 dB: Quiet home environment
  • 100 dB: Jet engine during takeoff (short exposure may cause hearing damage)

Section Summary

  • Intensity describes the power per unit area carried by a wave:
    [latex]I = \frac{P}{A}[/latex]

    where [latex]P[/latex] is the power and [latex]A[/latex] is the area the wave passes through.

  • For sound waves, intensity is also related to pressure amplitude:
    [latex]I = \frac{(\Delta p)^2}{2 \rho v_w}[/latex]

    where [latex]\Delta p[/latex] is pressure variation, [latex]\rho[/latex] is the density of the medium, and [latex]v_w[/latex] is the speed of sound.

  • The sound intensity level in decibels is given by:
    [latex]\beta\ (\text{dB}) = 10 \log_{10}\left(\frac{I}{I_0}\right)[/latex]

    where [latex]I_0 = 10^{-12}\ \text{W/m}^2[/latex] is the threshold of hearing.

Conceptual Questions

  1. Six members of a synchronized swim team wear earplugs to protect themselves against water pressure at depths, but they can still hear the music and perform the combinations in the water perfectly. One day, they were asked to leave the pool so the dive team could practice a few dives, and they tried to practice on a mat, but seemed to have a lot more difficulty. Why might this be?
  2. A community is concerned about a plan to bring train service to their downtown from the town’s outskirts. The current sound intensity level, even though the rail yard is blocks away, is 70 dB downtown. The mayor assures the public that there will be a difference of only 30 dB in sound in the downtown area. Should the townspeople be concerned? Why?

Problems & Exercises

  1. What is the intensity in watts per meter squared of 85.0-dB sound?
  2. The warning tag on a lawn mower states that it produces noise at a level of 91.0 dB. What is this in watts per meter squared?
  3. A sound wave traveling in [latex]20ºC[/latex] air has a pressure amplitude of 0.5 Pa. What is the intensity of the wave?
  4. What intensity level does the sound in the preceding problem correspond to?
  5. What sound intensity level in dB is produced by earphones that create an intensity of [latex]4.00×{\text{10}}^{\text{−2}}\phantom{\rule{0.25em}{0ex}}{\text{W/m}}^{\text{2}}[/latex]?
  6. Show that an intensity of [latex]{10}^{–12}\phantom{\rule{0.25em}{0ex}}{W/m}^{2}[/latex] is the same as [latex]{10}^{–16}\phantom{\rule{0.25em}{0ex}}{W/cm}^{2}[/latex].
  7. (a) What is the decibel level of a sound that is twice as intense as a 90.0-dB sound? (b) What is the decibel level of a sound that is one-fifth as intense as a 90.0-dB sound?
  8. (a) What is the intensity of a sound that has a level 7.00 dB lower than a [latex]4.00×{10}^{–9}\phantom{\rule{0.25em}{0ex}}{W/m}^{2}[/latex] sound? (b) What is the intensity of a sound that is 3.00 dB higher than a [latex]4.00×{10}^{–9}\phantom{\rule{0.25em}{0ex}}{W/m}^{2}[/latex] sound?
  9. (a) How much more intense is a sound that has a level 17.0 dB higher than another? (b) If one sound has a level 23.0 dB less than another, what is the ratio of their intensities?
  10. People with good hearing can perceive sounds as low in level as [latex]–8.00 dB[/latex] at a frequency of 3000 Hz. What is the intensity of this sound in watts per meter squared?
  11. If a large housefly 3.0 m away from you makes a noise of 40.0 dB, what is the noise level of 1000 flies at that distance, assuming interference has a negligible effect?
  12. Ten cars in a circle at a boom box competition produce a 120-dB sound intensity level at the center of the circle. What is the average sound intensity level produced there by each stereo, assuming interference effects can be neglected?
  13. The amplitude of a sound wave is measured in terms of its maximum gauge pressure. By what factor does the amplitude of a sound wave increase if the sound intensity level goes up by 40.0 dB?
  14. If a sound intensity level of 0 dB at 1000 Hz corresponds to a maximum gauge pressure (sound amplitude) of [latex]{10}^{–9}\phantom{\rule{0.25em}{0ex}}\text{atm}[/latex], what is the maximum gauge pressure in a 60-dB sound? What is the maximum gauge pressure in a 120-dB sound?
  15. An 8-hour exposure to a sound intensity level of 90.0 dB may cause hearing damage. What energy in joules falls on a 0.800-cm-diameter eardrum so exposed?
  16. (a) Ear trumpets were never very common, but they did aid people with hearing losses by gathering sound over a large area and concentrating it on the smaller area of the eardrum. What decibel increase does an ear trumpet produce if its sound gathering area is [latex]{900 cm}^{2}[/latex] and the area of the eardrum is [latex]{0.500 cm}^{2}[/latex], but the trumpet only has an efficiency of 5.00% in transmitting the sound to the eardrum? (b) Comment on the usefulness of the decibel increase found in part (a).
  17. Sound is more effectively transmitted into a stethoscope by direct contact than through the air, and it is further intensified by being concentrated on the smaller area of the eardrum. It is reasonable to assume that sound is transmitted into a stethoscope 100 times as effectively compared with transmission though the air. What, then, is the gain in decibels produced by a stethoscope that has a sound gathering area of [latex]{15.0 cm}^{2}[/latex], and concentrates the sound onto two eardrums with a total area of [latex]{0.900 cm}^{2}[/latex] with an efficiency of 40.0%?
  18. Loudspeakers can produce intense sounds with surprisingly small energy input in spite of their low efficiencies. Calculate the power input needed to produce a 90.0-dB sound intensity level for a 12.0-cm-diameter speaker that has an efficiency of 1.00%. (This value is the sound intensity level right at the speaker.)

Footnotes

  1. 1 Several government agencies and health-related professional associations recommend that 85 dB not be exceeded for 8-hour daily exposures in the absence of hearing protection.

Glossary

intensity
the power per unit area carried by a wave
sound intensity level
a unitless quantity telling you the level of the sound relative to a fixed standard
sound pressure level
the ratio of the pressure amplitude to a reference pressure
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book