"

Uniform Circular Motion and Gravitation

40 Satellites and Kepler’s Laws: An Argument for Simplicity

Learning Objectives

  • State and interpret Kepler’s three laws of planetary motion.

  • Derive Kepler’s third law for circular orbits using Newton’s laws.

  • Understand the historical context and limitations of the Ptolemaic model of the universe.

Gravitational Orbits: A Universal Phenomenon

From the Moon’s orbit around Earth to artificial satellites and distant star systems, gravitationally bound orbits are everywhere. These orbits include:

  • Earth’s natural and artificial satellites

  • Planetary orbits around the Sun

  • Binary star systems

  • Galaxy clusters held together by mutual gravitational attraction

Although real-world gravitational systems can be complex and require numerical computation, many important insights come from examining simplified orbital models governed purely by Newtonian gravity.

    Simplifying Assumptions for Orbital Motion

    To explore orbital motion analytically, we consider a special but very common case:

    • A small mass [latex]m[/latex] (e.g., a satellite or planet) orbits a much larger mass [latex]M[/latex] (e.g., a planet or star).

    • The gravitational interaction dominates, and outside influences from other bodies are negligible.

    • The center of mass lies within [latex]M[/latex], allowing us to approximate it as stationary.

    This idealization applies to:

    • The Moon orbiting Earth

    • Earth and other planets orbiting the Sun

    • Moons of Jupiter, Saturn, and other planets

    • Artificial satellites orbiting Earth

    These assumptions provide the foundation for understanding Kepler’s laws of planetary motion.

    Kepler’s Laws of Planetary Motion

    Developed by Johannes Kepler in the early 1600s, these laws describe planetary orbits based on the extensive astronomical data collected by Tycho Brahe. Though originally formulated to describe planets orbiting the Sun, Kepler’s laws apply to any object in gravitational orbit under the conditions noted above.

    Kepler’s First Law: Elliptical Orbits

    The orbit of each planet is an ellipse, with the Sun at one focus.

    An ellipse is a closed, elongated curve defined by two fixed points called foci. The sum of the distances from any point on the ellipse to each focus is constant (Figure 40.1a). A circle is a special case of an ellipse in which both foci coincide.

    For any gravitationally bound object orbiting another, the path is elliptical, with the more massive body (e.g., the Sun or a planet) located at one focus (Figure 40.1b).

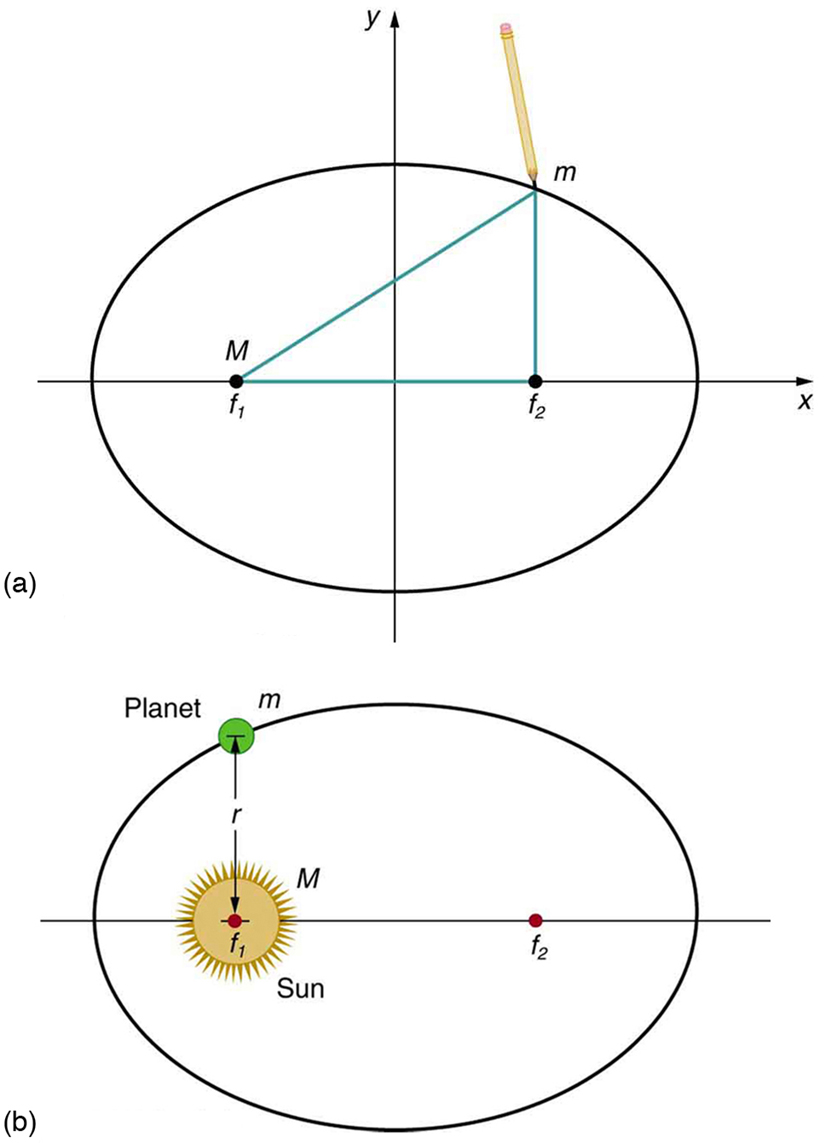
    In figure a, an ellipse is shown on the coordinate axes. Two foci of the ellipse are joined to a point m on the ellipse. A pencil is shown at the point m. In figure b the elliptical path of a planet is shown. At the left focus f-one of the path the Sun is shown. The planet is shown just above the Sun on the elliptical path.
    Figure 40.1: (a) An ellipse traced with two foci shows the geometric definition.
    (b) In a gravitational orbit, the smaller body [latex]m[/latex] moves around the larger mass [latex]M[/latex] along an elliptical path with [latex]M[/latex] at one focus.

    Kepler’s Second Law: Equal Areas in Equal Times

    A line drawn from the orbiting object to the central body sweeps out equal areas in equal intervals of time.

    This law implies that the object moves faster when it is closer to the central mass and slower when it is farther away (Figure 40.2). The varying speed maintains the constant areal rate of motion, a consequence of conservation of angular momentum.

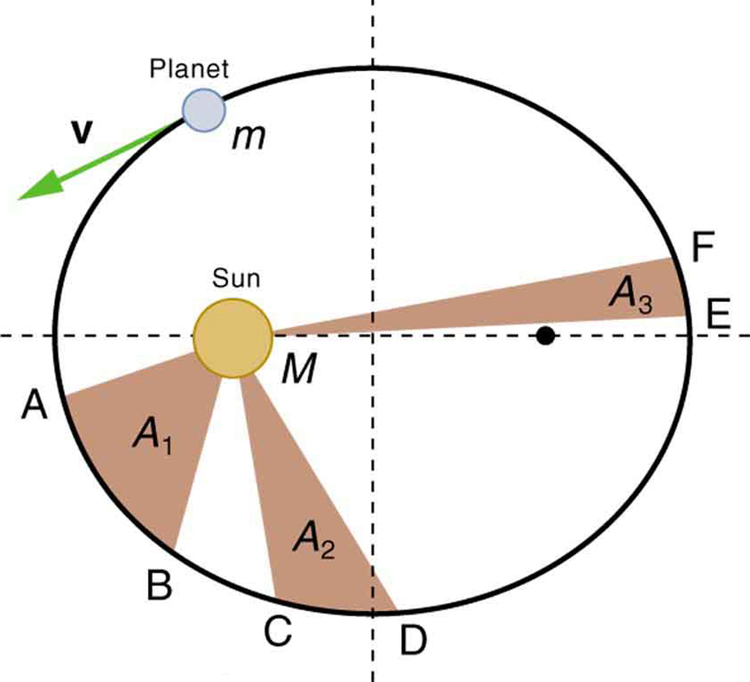
    In the figure, the elliptical path of a planet is shown. The Sun is at the left focus. Three shaded regions M A B, M C D and M E F are marked on the figure by joining the Sun to the three pairs of points A B, C D, and E F on the elliptical path. The velocity of the planet is shown on the planet in a direction tangential to the path.
    Figure 40.2: Equal area segments (A–B, C–D, E–F) are swept in equal time intervals. The planet moves faster near perihelion (closest point) and slower near aphelion (farthest point).

    Kepler’s Third Law: Harmonic Law

    The square of the orbital period of a planet is proportional to the cube of the average orbital radius.

    Mathematically:

    [latex]\frac{T_1^2}{T_2^2} = \frac{r_1^3}{r_2^3}[/latex]

    Here:

    • [latex]T_1[/latex] and [latex]T_2[/latex] are the orbital periods of two planets, and

    • [latex]r_1[/latex] and [latex]r_2[/latex] are their respective average orbital radii.

    This relation applies only when both small masses orbit the same large central mass. The law is empirical—it describes the motion but does not explain the underlying cause. The physical origin (gravitational force) was later provided by Newton.

    💡 Note: While Kepler formulated his laws for planets orbiting the Sun, these laws apply more generally to any gravitational two-body system where a small mass orbits a much larger one.

    Example 40.2: Find the Time for One Orbit of an Earth Satellite

    Given that the Moon orbits Earth each 27.3 d and that it is an average distance of [latex]3.84×{\text{10}}^{8}\phantom{\rule{0.25em}{0ex}}\text{m}[/latex] from the center of Earth, calculate the period of an artificial satellite orbiting at an average altitude of 1500 km above Earth’s surface.

    Strategy

    The period, or time for one orbit, is related to the radius of the orbit by Kepler’s third law, given in mathematical form in [latex]\frac{{T}_{1}^{ 2}}{{T}_{2}^{ 2}}=\frac{{r}_{1}^{ 3}}{{r}_{2}^{ 3}}[/latex]. Let us use the subscript 1 for the Moon and the subscript 2 for the satellite. We are asked to find [latex]{T}_{2}[/latex]. The given information tells us that the orbital radius of the Moon is [latex]{r}_{1}=3\text{.}\text{84}×{\text{10}}^{8}\phantom{\rule{0.25em}{0ex}}\text{m}[/latex], and that the period of the Moon is [latex]{T}_{1}=\text{27.3 d}[/latex]. The height of the artificial satellite above Earth’s surface is given, and so we must add the radius of Earth (6380 km) to get [latex]{r}_{2}=\left(\text{1500}+\text{6380}\right)\phantom{\rule{0.25em}{0ex}}\text{km}=\text{7880}\phantom{\rule{0.25em}{0ex}}\text{km}[/latex]. Now all quantities are known, and so [latex]{T}_{2}[/latex] can be found.

    Solution

    Kepler’s third law is

    [latex]\frac{{T}_{1}^{ 2}}{{T}_{2}^{ 2}}=\frac{{r}_{1}^{ 3}}{{r}_{2}^{ 3}}\text{.}[/latex]

    To solve for [latex]{T}_{2}[/latex], we cross-multiply and take the square root, yielding

    [latex]{T}_{2}^{ 2}={T}_{1}^{ 2}{\left(\frac{{r}_{2}}{{r}_{1}}\right)}^{3}[/latex]
    [latex]{T}_{2}={T}_{1}{\left(\frac{{r}_{2}}{{r}_{1}}\right)}^{3/2}\text{.}[/latex]

    Substituting known values yields

    [latex]\begin{array}{lll}{T}_{2}& =& \text{27.3 d}×\frac{\text{24.0 h}}{\text{d}}×{\left(\frac{\text{7880 km}}{3.84×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{km}}\right)}^{3/2}\\ & =& \text{1.93 h.}\end{array}[/latex]

    Discussion

    This is a reasonable period for a satellite in a fairly low orbit. It is interesting that any satellite at this altitude will orbit in the same amount of time. This fact is related to the condition that the satellite’s mass is small compared with that of Earth.

    Newton’s Laws Lead to Kepler’s Third Law

    Let us derive Kepler’s third law using Newton’s law of gravitation and Newton’s second law. Consider a satellite of mass [latex]m[/latex] orbiting a much larger central mass [latex]M[/latex] (e.g., a planet orbiting the Sun). We assume a circular orbit for simplicity. Gravity provides the centripetal force that keeps the satellite in orbit:

    [latex]F_{\text{net}} = ma_{\text{c}} = m \frac{v^2}{r}[/latex]

    Now, applying Newton’s law of universal gravitation as the source of this centripetal force:

    [latex]F_{\text{gravity}} = G \frac{mM}{r^2}[/latex]

    Equating the two forces:

    [latex]G \frac{mM}{r^2} = m \frac{v^2}{r}[/latex]

    Canceling [latex]m[/latex] from both sides and solving for [latex]v^2[/latex]:

    [latex]G \frac{M}{r} = v^2[/latex]

    Since the orbital speed [latex]v[/latex] is related to the period [latex]T[/latex] of revolution by the circumference of the orbit:

    [latex]v = \frac{2\pi r}{T}[/latex]

    Substitute this into the expression for [latex]v^2[/latex]:

    [latex]G \frac{M}{r} = \left(\frac{2\pi r}{T}\right)^2 = \frac{4\pi^2 r^2}{T^2}[/latex]

    Solving for [latex]T^2[/latex]:

    [latex]T^2 = \frac{4\pi^2}{GM} r^3[/latex]

    This shows that for any object orbiting the same central mass [latex]M[/latex], the square of the orbital period is proportional to the cube of the orbital radius:

    [latex]\frac{T_1^2}{T_2^2} = \frac{r_1^3}{r_2^3}[/latex]

    This is Kepler’s third law. It applies to all satellites orbiting the same parent body.

    Using Kepler’s Third Law to Determine Mass

    Rewriting the result:

    [latex]\frac{r^3}{T^2} = \frac{GM}{4\pi^2}[/latex]

    This formula allows us to determine the mass [latex]M[/latex] of the central body if we know the satellite’s orbital radius and period. This method has been extensively used to calculate the masses of stars, planets, and galaxies.

    Table of Orbital Data and [latex]r^3 / T^2[/latex] Ratios

    The table below shows orbital data for various bodies orbiting the Sun and Jupiter. The values of [latex]r^3 / T^2[/latex] remain constant (to within measurement uncertainty), confirming the predictive power of Kepler’s third law and Newtonian gravity.

    Table 40.1: Orbital Data and Kepler’s Third Law
    Parent Satellite Average orbital radius r(km) Period T(y) r3 / T2 (km3 / y2)
    Earth Moon [latex]3.84×{\text{10}}^{5}[/latex] 0.07481 [latex]1\text{.}\text{01}×{\text{10}}^{\text{19}}[/latex]
    Sun Mercury [latex]5\text{.}\text{79}×{\text{10}}^{7}[/latex] 0.2409 [latex]3\text{.}\text{34}×{\text{10}}^{\text{24}}[/latex]
    Venus [latex]1\text{.}\text{082}×{\text{10}}^{8}[/latex] 0.6150 [latex]3\text{.}\text{35}×{\text{10}}^{\text{24}}[/latex]
    Earth [latex]1\text{.}\text{496}×{\text{10}}^{8}[/latex] 1.000 [latex]3\text{.}\text{35}×{\text{10}}^{\text{24}}[/latex]
    Mars [latex]2\text{.}\text{279}×{\text{10}}^{8}[/latex] 1.881 [latex]3\text{.}\text{35}×{\text{10}}^{\text{24}}[/latex]
    Jupiter [latex]7\text{.}\text{783}×{\text{10}}^{8}[/latex] 11.86 [latex]3\text{.}\text{35}×{\text{10}}^{\text{24}}[/latex]
    Saturn [latex]1\text{.}\text{427}×{\text{10}}^{9}[/latex] 29.46 [latex]3\text{.}\text{35}×{\text{10}}^{\text{24}}[/latex]
    Neptune [latex]4\text{.}\text{497}×{\text{10}}^{9}[/latex] 164.8 [latex]3\text{.}\text{35}×{\text{10}}^{\text{24}}[/latex]
    Pluto [latex]5\text{.}\text{90}×{\text{10}}^{9}[/latex] 248.3 [latex]3\text{.}\text{33}×{\text{10}}^{\text{24}}[/latex]
    Jupiter Io [latex]4\text{.}\text{22}×{\text{10}}^{5}[/latex] 0.00485 (1.77 d) [latex]3\text{.}\text{19}×{\text{10}}^{\text{21}}[/latex]
    Europa [latex]6\text{.}\text{71}×{\text{10}}^{5}[/latex] 0.00972 (3.55 d) [latex]3\text{.}\text{20}×{\text{10}}^{\text{21}}[/latex]
    Ganymede [latex]1\text{.}\text{07}×{\text{10}}^{6}[/latex] 0.0196 (7.16 d) [latex]3\text{.}\text{19}×{\text{10}}^{\text{21}}[/latex]
    Callisto [latex]1\text{.}\text{88}×{\text{10}}^{6}[/latex] 0.0457 (16.19 d) [latex]3\text{.}\text{20}×{\text{10}}^{\text{21}}[/latex]

    Small deviations arise due to:

    • Uncertainties in measurement

    • Gravitational perturbations by other bodies

    Such perturbations have even led to the discovery of new planets and moons, a triumph of Newtonian gravity.

    Simplicity and the Power of Universal Laws

    Kepler’s laws describe planetary motion, but Newton’s gravitational theory explains them. This marked a shift in science—from description to causation through universal laws.

    “Truth is ever to be found in simplicity.” — Isaac Newton

    The Copernican model (Figure 40.3(b)) exemplifies this simplicity, explaining planetary motion using a few core principles. By contrast, the Ptolemaic model (Figure 40.3(a)) relied on complex geometrical constructions without causal explanation.

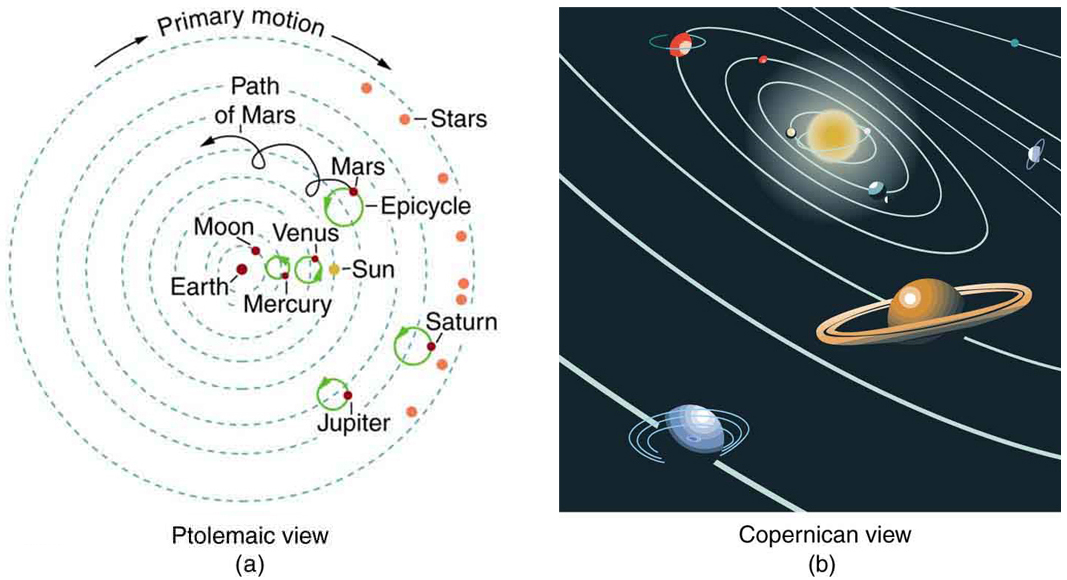
    In figure a the paths of the different planets are shown in the forms of dotted concentric circles with the Earth at the center with its Moon. The Sun is also shown revolving around the Earth. Each planet is labeled with its name. On the planets Mercury, Venus, Mars, Jupiter and Saturn green colored epicycles are shown. In the figure b Copernican view of planet is shown. The Sun is shown at the center of the solar system. The planets are shown moving around the Sun.
    Figure 40.3:(a) Ptolemaic model: Earth at the center; planets and stars revolve in complex, nested circular paths. (b) Copernican-Newtonian model: The Sun at the center, governed by universal laws of motion and gravity.

    Section Summary

    • Kepler’s third law states that [latex]T^2 \propto r^3[/latex] for orbiting bodies.

    • It can be derived from Newton’s second law and his law of gravitation.

    • The resulting formula [latex]T^2 = \frac{4\pi^2}{GM} r^3[/latex] connects orbit period to central mass and radius.

    • These ideas highlight the unity and simplicity of physics, showing how one fundamental force explains a wide variety of natural phenomena.

    Conceptual Questions

    1. In what frame(s) of reference are Kepler’s laws valid? Are Kepler’s laws purely descriptive, or do they contain causal information?

    Problem Exercises

    1. A geosynchronous Earth satellite is one that has an orbital period of precisely 1 day. Such orbits are useful for communication and weather observation because the satellite remains above the same point on Earth (provided it orbits in the equatorial plane in the same direction as Earth’s rotation). Calculate the radius of such an orbit based on the data for the moon in Table 40.1.
    2. Calculate the mass of the Sun based on data for Earth’s orbit and compare the value obtained with the Sun’s actual mass.
    3. Find the mass of Jupiter based on data for the orbit of one of its moons, and compare your result with its actual mass.
    4. Find the ratio of the mass of Jupiter to that of Earth based on data in Table 40.1
    5. Astronomical observations of our Milky Way galaxy indicate that it has a mass of about [latex]8\text{.}0×{\text{10}}^{\text{11}}[/latex] solar masses. A star orbiting on the galaxy’s periphery is about [latex]6\text{.}0×{\text{10}}^{4}[/latex] light years from its center. (a) What should the orbital period of that star be? (b) If its period is [latex]6\text{.}0×{\text{10}}^{7}[/latex] instead, what is the mass of the galaxy? Such calculations are used to imply the existence of “dark matter” in the universe and have indicated, for example, the existence of very massive black holes at the centers of some galaxies.
    6. Integrated Concepts Space debris left from old satellites and their launchers is becoming a hazard to other satellites. (a) Calculate the speed of a satellite in an orbit 900 km above Earth’s surface. (b) Suppose a loose rivet is in an orbit of the same radius that intersects the satellite’s orbit at an angle of [latex]\text{90º}[/latex] relative to Earth. What is the velocity of the rivet relative to the satellite just before striking it? (c) Given the rivet is 3.00 mm in size, how long will its collision with the satellite last? (d) If its mass is 0.500 g, what is the average force it exerts on the satellite? (e) How much energy in joules is generated by the collision? (The satellite’s velocity does not change appreciably, because its mass is much greater than the rivet’s.)
    7. Unreasonable Results (a) Based on Kepler’s laws and information on the orbital characteristics of the Moon, calculate the orbital radius for an Earth satellite having a period of 1.00 h. (b) What is unreasonable about this result? (c) What is unreasonable or inconsistent about the premise of a 1.00 h orbit?
    8. Construct Your Own Problem On February 14, 2000, the NEAR spacecraft was successfully inserted into orbit around Eros, becoming the first artificial satellite of an asteroid. Construct a problem in which you determine the orbital speed for a satellite near Eros. You will need to find the mass of the asteroid and consider such things as a safe distance for the orbit. Although Eros is not spherical, calculate the acceleration due to gravity on its surface at a point an average distance from its center of mass. Your instructor may also wish to have you calculate the escape velocity from this point on Eros.

    License

    Icon for the Creative Commons Attribution 4.0 International License

    College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

    Share This Book