"

Rotational motion and angular momentum

71 Rotational Kinetic Energy: Work and Energy Revisited

Learning Objectives

  • Derive the equation for rotational work
  • Calculate rotational kinetic energy
  • Demonstrate the Law of Conservation of Energy in rotational systems

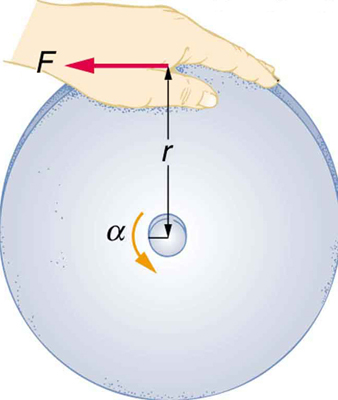
Rotational motion, like linear motion, involves both force and energy. For example, in Figure 71.1, a worker uses an electric grindstone to cut metal. The sparks, noise, and heat are all results of the energy that was transferred into the grindstone by the motor. The grindstone continues to rotate even after the motor is shut off, eventually slowing down due to friction. What energy keeps it spinning? It’s called rotational kinetic energy, a rotational counterpart to the kinetic energy of translational motion.

The figure shows a mechanic cutting metal with a metal grinder. The sparks are emerging from the point of contact and jumping off tangentially from the cutter.
Figure 71.1 A motor spins this grindstone, increasing its rotational kinetic energy. That energy is later dissipated as heat, light, sound, and vibration. (credit: U.S. Navy photo by Mass Communication Specialist Seaman Zachary David Bell)

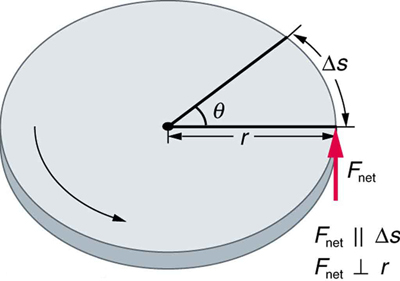
To get the grindstone spinning, work must be done. Just like in translational motion, we can define work in rotational motion. When a net force is applied perpendicular to the radius of a rotating object (as in Figure 71.2), the displacement is along the direction of the force, so the net work done is:

[latex]\text{net}\,W = (\text{net}\,F)\,\Delta s[/latex]

To connect this with torque and angular displacement, we multiply and divide the right-hand side by the radius [latex]r[/latex]:

[latex]\text{net}\,W = (r\,\text{net}\,F)\,\frac{\Delta s}{r}[/latex]

Recognizing that [latex]r\,\text{net}\,F = \text{net}\,\tau[/latex] (torque) and [latex]\Delta s/r = \theta[/latex] (angular displacement in radians), we arrive at the expression for rotational work:

[latex]\text{net}\,W = (\text{net}\,\tau)\,\theta[/latex]
The figure shows a circular disc of radius r. A net force F is applied perpendicular to the radius, rotating the disc in an anti-clockwise direction and producing a displacement equal to delta S, in a direction parallel to the direction of the force applied. The angle covered is theta.
Figure 71.2 A force applied perpendicular to the radius of a disk causes rotational motion. The displacement is tangent to the circle, and the torque causes angular acceleration. The work done increases the disk’s rotational kinetic energy.

We now want to derive an expression for rotational kinetic energy. Since [latex]\text{net}\,\tau = I\,\alpha[/latex], where [latex]I[/latex] is the moment of inertia and [latex]\alpha[/latex] is angular acceleration, we substitute into the equation for work:

[latex]\text{net}\,W = I\,\alpha\,\theta[/latex]

From rotational kinematics, we know:

[latex]\omega^2 = \omega_0^2 + 2\,\alpha\,\theta[/latex]

Solving for [latex]\alpha\,\theta[/latex], we get:

[latex]\alpha\,\theta = \frac{\omega^2 - \omega_0^2}{2}[/latex]

Substituting this back into the expression for net work:

[latex]\text{net}\,W = \frac{1}{2}I\,\omega^2 - \frac{1}{2}I\,\omega_0^2[/latex]

This is the work-energy theorem for rotational motion. It tells us that the net work done on a rotating object changes its rotational kinetic energy:

[latex]KE_{\text{rot}} = \frac{1}{2}I\,\omega^2[/latex]

This mirrors the translational kinetic energy equation [latex]KE = \frac{1}{2}mv^2[/latex], but here mass [latex]m[/latex] is replaced by moment of inertia [latex]I[/latex], and velocity [latex]v[/latex] is replaced by angular velocity [latex]\omega[/latex].

Rotational kinetic energy can be stored and used in mechanical systems. For example, some experimental buses store rotational energy using a large flywheel, as shown in Figure 71.3. When going downhill or braking, energy is stored in the spinning flywheel. Later, the flywheel’s energy can be used to accelerate the vehicle again, reducing the energy lost to friction and braking.

The figure shows a bus carrying a large flywheel on its board in which rotational kinetic energy is stored.
Figure 71.3 Some experimental buses store energy using a heavy flywheel. When braking or descending a hill, the bus transfers energy into the spinning flywheel. This energy can later be used to help the bus accelerate, demonstrating rotational kinetic energy conservation.

Making Connections

Work and energy in rotational motion are completely analogous to work and energy in translational motion, first introduced in Uniform Circular Motion and Gravitation.

We now solve a key rotational kinematic equation to help derive an expression for rotational work and energy. Starting from:

[latex]\omega^2 = \omega_0^2 + 2\alpha\theta[/latex]

Solving for the product [latex]\alpha \theta[/latex] gives:

[latex]\alpha \theta = \frac{\omega^2 - \omega_0^2}{2}[/latex]

We substitute this into the earlier expression for net rotational work, where [latex]\tau = I\alpha[/latex]:

[latex]\text{net } W = I\alpha\theta = \frac{1}{2}I\omega^2 - \frac{1}{2}I\omega_0^2[/latex]

This equation is the work-energy theorem for rotational motion. Just like in linear motion, net work results in a change in kinetic energy.

By analogy, we define the quantity

[latex]\text{KE}_{\text{rot}} = \frac{1}{2}I\omega^2[/latex]

as the rotational kinetic energy of an object, where [latex]I[/latex] is its moment of inertia and [latex]\omega[/latex] its angular velocity. This formula mirrors translational kinetic energy: [latex]\text{KE} = \frac{1}{2}mv^2[/latex], where [latex]I[/latex] replaces [latex]m[/latex] and [latex]\omega[/latex] replaces [latex]v[/latex].

Rotational kinetic energy has many applications. In biomechanical systems, it describes the motion of limbs, tools, and even the internal workings of joints. In engineering, flywheels use this energy for motion stabilization and energy storage. For instance, in experimental vehicles, large rotating flywheels store energy while driving downhill or braking. This energy can later be used to accelerate or climb inclines efficiently.

Calculating the Work and Energy for Spinning a Grindstone

Consider a person who spins a large grindstone by placing her hand on its edge and exerting a force through part of a revolution as shown in Figure 71.4. In this example, we verify that the work done by the torque she exerts equals the change in rotational energy. (a) How much work is done if she exerts a force of 200 N through a rotation of [latex]\text{1.00 rad}\left(57.3º\right)[/latex]? The force is kept perpendicular to the grindstone’s 0.320-m radius at the point of application, and the effects of friction are negligible. (b) What is the final angular velocity if the grindstone has a mass of 85.0 kg? (c) What is the final rotational kinetic energy? (It should equal the work.)

Strategy

To find the work, we can use the equation [latex]\text{net}\phantom{\rule{0.25em}{0ex}}W=\left(\text{net τ}\right)\theta[/latex]. We have enough information to calculate the torque and are given the rotation angle. In the second part, we can find the final angular velocity using one of the kinematic relationships. In the last part, we can calculate the rotational kinetic energy from its expression in [latex]{\text{KE}}_{\text{rot}}=\frac{1}{2}{\mathrm{I\omega }}^{2}[/latex].

Solution for (a)

The net work is expressed in the equation

[latex]\text{net}\phantom{\rule{0.25em}{0ex}}W=\left(\text{net τ}\right)\theta ,[/latex]

where net [latex]\tau[/latex] is the applied force multiplied by the radius [latex]\left(\text{rF}\right)[/latex] because there is no retarding friction, and the force is perpendicular to [latex]r[/latex]. The angle [latex]\theta[/latex] is given. Substituting the given values in the equation above yields

[latex]\begin{array}{lll}\text{net}\phantom{\rule{0.25em}{0ex}}W& =& \text{rF}\theta =\left(\text{0.320 m}\right)\left(\text{200 N}\right)\left(\text{1.00 rad}\right)\\ & =& \text{64.0 N}\cdot \text{m.}\end{array}[/latex]

Noting that [latex]1 N·\text{m}=1 J[/latex],

[latex]\text{net}\phantom{\rule{0.25em}{0ex}}W=\text{64.0 J}.[/latex]
The figure shows a large grindstone of radius r which is being given a spin by applying a force F in a counterclockwise direction, as indicated by the arrows.
Figure 71.4 A large grindstone is given a spin by a person grasping its outer edge.

Solution for (b)

To find [latex]\omega[/latex] from the given information requires more than one step. We start with the kinematic relationship in the equation

[latex]{\omega }^{2}={{\omega }_{\text{0}}}^{2}+2\text{αθ}.[/latex]

Note that [latex]{\omega }_{0}=0[/latex] because we start from rest. Taking the square root of the resulting equation gives

[latex]\omega ={\left(2\text{αθ}\right)}^{1/2}.[/latex]

Now we need to find [latex]\alpha[/latex]. One possibility is

[latex]\alpha =\frac{\text{net τ}}{I},[/latex]

where the torque is

[latex]\text{net τ}=\text{rF}=\left(\text{0.320 m}\right)\left(\text{200 N}\right)=\text{64.0 N}\cdot \text{m}.[/latex]

The formula for the moment of inertia for a disk is found in Making Connections:

[latex]I=\frac{1}{2}{\text{MR}}^{2}=0.5\left(\text{85.0 kg}\right){\left(\text{0.320 m}\right)}^{2}=\text{4.352 kg}\cdot {\text{m}}^{2}.[/latex]

Substituting the values of torque and moment of inertia into the expression for [latex]\alpha[/latex], we obtain

[latex]\alpha =\frac{\text{64}\text{.}\text{0 N}\cdot \text{m}}{\text{4.352 kg}\cdot {\text{m}}^{2}}=\text{14.7}\frac{\text{rad}}{{\text{s}}^{2}}.[/latex]

Now, substitute this value and the given value for [latex]\theta[/latex] into the above expression for [latex]\omega[/latex]:

[latex]\omega ={\left(2\text{αθ}\right)}^{1/2}={\left[2\left(\text{14.7}\frac{\text{rad}}{{\text{s}}^{2}}\right)\left(\text{1.00 rad}\right)\right]}^{1/2}=\text{5.42}\frac{\text{rad}}{\text{s}}.[/latex]

Solution for (c)

The final rotational kinetic energy is

[latex]{\text{KE}}_{\text{rot}}=\frac{1}{2}{\mathrm{I\omega }}^{2}.[/latex]

Both [latex]I[/latex] and [latex]\omega[/latex] were found above. Thus,

[latex]{\text{KE}}_{\text{rot}}=\left(0.5\right)\left(\text{4.352 kg}\cdot {\text{m}}^{2}\right){\left(\text{5.42 rad/s}\right)}^{2}=\text{64.0 J}.[/latex]

Discussion

The final rotational kinetic energy equals the work done by the torque, which confirms that the work done went into rotational kinetic energy. We could, in fact, have used an expression for energy instead of a kinematic relation to solve part (b). We will do this in later examples.

Helicopter pilots are acutely aware of the importance of rotational kinetic energy. During flight, if the rotor blades slow below a certain critical angular velocity, they lose lift, and the aircraft may become uncontrollable. Restarting the blades requires significant energy input, and if that energy isn’t available fast enough, a crash may result. This is because helicopter engines are typically optimized for steady lift—not for rapidly re-energizing the rotor system after a loss in rotational speed.

Before takeoff, rotational kinetic energy is built up in the blades. It is crucial that this energy not be allowed to fall below the threshold required for lift. If the rotors begin to slow mid-flight, and there is enough altitude, pilots can perform a maneuver called autorotation. This controlled descent uses the helicopter’s gravitational potential energy to spin the blades faster, restoring rotational kinetic energy. However, if the helicopter is already too close to the ground, there may not be enough time or height to recover lift, leading to catastrophic failure.

Problem-Solving Strategy for Rotational Energy

  1. Determine that energy or work is involved in the rotation. Look for torque, angular velocity, or changing angular motion.
  2. Determine the system of interest. Sketching the physical setup can help clarify what is included in your energy accounting.
  3. Analyze the situation to determine the types of work and energy involved. These may include rotational kinetic energy, gravitational potential energy, and work done by friction or external forces.
  4. For closed systems, apply conservation of mechanical energy:
    [latex]{\text{KE}}_{\text{i}} + {\text{PE}}_{\text{i}} = {\text{KE}}_{\text{f}} + {\text{PE}}_{\text{f}}[/latex]

    Note: [latex]{\text{KE}}[/latex] can include both translational and rotational kinetic energy.

  5. For open systems, identify energy transfers or losses—such as heat, sound, or deformation—and account for them with an “other energy” term ([latex]\text{OE}[/latex]) if needed.
  6. Eliminate or simplify terms whenever possible. For example, if potential energy is unchanged or friction is negligible, drop those terms from the equation.
  7. Check your answer. Does it have reasonable units? Does it match physical intuition (e.g., energy must be non-negative)?

Calculating Helicopter Energies

A typical small rescue helicopter, similar to the one in Figure 71.5, has four blades, each is 4.00 m long and has a mass of 50.0 kg. The blades can be approximated as thin rods that rotate about one end of an axis perpendicular to their length. The helicopter has a total loaded mass of 1000 kg. (a) Calculate the rotational kinetic energy in the blades when they rotate at 300 rpm. (b) Calculate the translational kinetic energy of the helicopter when it flies at 20.0 m/s, and compare it with the rotational energy in the blades. (c) To what height could the helicopter be raised if all of the rotational kinetic energy could be used to lift it?

The given figure here shows a helicopter from the Auckland Westpac Rescue Helicopter Service over a sea. A rescue diver is shown holding the iron stand bar at the bottom of the helicopter, clutching a person. In the other image just above this, the blades of the helicopter are shown with their anti-clockwise rotation direction shown with an arrow and the length of one blade is given as four meters.
Figure 71.5. The first image shows how helicopters store large amounts of rotational kinetic energy in their blades. This energy must be put into the blades before takeoff and maintained until the end of the flight. The engines do not have enough power to simultaneously provide lift and put significant rotational energy into the blades. The second image shows a helicopter from the Auckland Westpac Rescue Helicopter Service. Over 50,000 lives have been saved since its operations beginning in 1973. Here, a water rescue operation is shown. (credit: 111 Emergency, Flickr)

Strategy

Rotational and translational kinetic energies can be calculated from their definitions. The last part of the problem relates to the idea that energy can change form, in this case from rotational kinetic energy to gravitational potential energy.

Solution for (a)

The rotational kinetic energy is

[latex]{\text{KE}}_{\text{rot}}=\frac{1}{2}{\mathrm{I\omega }}^{2}.[/latex]

We must convert the angular velocity to radians per second and calculate the moment of inertia before we can find [latex]{\text{KE}}_{\text{rot}}[/latex]. The angular velocity [latex]\omega[/latex] is

[latex]\omega =\frac{\text{300 rev}}{\text{1.00 min}}\cdot \frac{\text{2π rad}}{\text{1 rev}}\cdot \frac{\text{1.00 min}}{\text{60.0 s}}=\text{31.4}\frac{\text{rad}}{\text{s}}.[/latex]

The moment of inertia of one blade will be that of a thin rod rotated about its end, found in Figure 69.3. The total [latex]I[/latex] is four times this moment of inertia, because there are four blades. Thus,

[latex]I=4\frac{{\mathrm{M\ell }}^{2}}{3}=4×\frac{\left(\text{50.0 kg}\right){\left(\text{4.00 m}\right)}^{2}}{3}=\text{1067 kg}\cdot {\text{m}}^{2}.[/latex]

Entering [latex]\omega[/latex] and [latex]I[/latex] into the expression for rotational kinetic energy gives

[latex]\begin{array}{lll}{\text{KE}}_{\text{rot}}& =& 0.5\left(\text{1067 kg}\cdot {\text{m}}^{2}\right){\left(\text{31.4 rad/s}\right)}^{2}\\ & =& 5.26×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{J}\end{array}[/latex]

Solution for (b)

Translational kinetic energy was defined in Uniform Circular Motion and Gravitation. Entering the given values of mass and velocity, we obtain

[latex]{\text{KE}}_{\text{trans}}=\frac{1}{2}{\mathit{mv}}^{2}=\left(0.5\right)\left(\text{1000 kg}\right){\left(\text{20.0 m/s}\right)}^{2}=2\text{.}\text{00}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{J}.[/latex]

To compare kinetic energies, we take the ratio of translational kinetic energy to rotational kinetic energy. This ratio is

[latex]\frac{2\text{.}\text{00}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{J}}{5\text{.}\text{26}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{J}}=0.380.[/latex]

Solution for (c)

At the maximum height, all rotational kinetic energy will have been converted to gravitational energy. To find this height, we equate those two energies:

[latex]{\text{KE}}_{\text{rot}}={\text{PE}}_{\text{grav}}[/latex]

or

[latex]\frac{1}{2}{\mathrm{I\omega }}^{2}=\text{mgh}.[/latex]

We now solve for [latex]h[/latex] and substitute known values into the resulting equation

[latex]h=\frac{{\frac{1}{2}\mathrm{I\omega }}^{2}}{\text{mg}}=\frac{5.26×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{J}}{\left(\text{1000 kg}\right)\left(9.80\phantom{\rule{0.25em}{0ex}}{\text{m/s}}^{2}\right)}=\text{53.7 m}.[/latex]

Discussion

The ratio of translational energy to rotational kinetic energy is only 0.380. This ratio tells us that most of the kinetic energy of the helicopter is in its spinning blades—something you probably would not suspect. The 53.7 m height to which the helicopter could be raised with the rotational kinetic energy is also impressive, again emphasizing the amount of rotational kinetic energy in the blades.

Making Connections

Conservation of energy applies equally to rotational motion, since rotational kinetic energy is simply another form of [latex]\text{KE}[/latex]. A more general discussion of energy conservation was introduced in Uniform Circular Motion and Gravitation.

How Thick Is the Soup? Or Why Don’t All Objects Roll Downhill at the Same Rate?

In a tomato soup factory, cans filled with soup are tested by rolling them down a ramp. If a can rolls too quickly, it means the soup inside is too thin. But why would cans of identical mass and shape roll at different speeds? And why would thicker soup make the can roll more slowly?

The answer lies in energy conservation. Assume that all the cans begin at rest and roll down the ramp without slipping. Each can starts with the same gravitational potential energy [latex]{\text{PE}}_{\text{grav}}[/latex], and this energy is converted entirely into kinetic energy as they move. However, the total kinetic energy includes both translational and rotational parts:

[latex]{\text{KE}} = {\text{KE}}_{\text{trans}} + {\text{KE}}_{\text{rot}}[/latex]

If a can rolls, some of the gravitational potential energy is transformed into rotational motion. That leaves less energy available for translational motion—so the can rolls more slowly than if it simply slid down the ramp. The thinner soup inside the can does not rotate with the can’s shell, so less energy is used for rotation. The thicker soup sticks to the can, rotating with it, and uses more of the initial energy as rotational kinetic energy. As a result, the can with thicker soup reaches the bottom last. This concept is illustrated in Figure 71.6.

The figure shows a flat surface inclined at a height of h from the surface level, with three cans of soup of different densities numbered as one, two, and three rolling along it.
Figure 71.6 Three cans of soup with identical masses race down an incline. The can that slides without rolling wins because all its gravitational potential energy becomes translational kinetic energy. The second can, containing thin soup, rolls without slipping and finishes second because some of the energy becomes rotational. The third can, with thick soup, rotates fully with the can and finishes last due to more energy going into rotation.

If we ignore frictional losses, then gravity is the only force doing work. Applying conservation of energy, we find that:

[latex]{\text{PE}}_{\text{i}} = {\text{KE}}_{\text{f}}[/latex]

More specifically:

[latex]{\text{PE}}_{\text{grav}} = {\text{KE}}_{\text{trans}} + {\text{KE}}_{\text{rot}}[/latex]

In terms of variables:

[latex]mgh = \frac{1}{2}mv^2 + \frac{1}{2}I\omega^2[/latex]

This equation shows that the gravitational potential energy [latex]mgh[/latex] is divided between translational and rotational kinetic energy. The greater the moment of inertia [latex]I[/latex], the more energy goes into rotation and the slower the translation. If a can slides rather than rolls, then [latex]\omega = 0[/latex] and the entire energy goes into translational motion, making it faster.

Take-Home Experiment

Collect several unopened cans containing different types of food. Before conducting the experiment, predict which can will reach the bottom of a ramp first. Justify your prediction using concepts of rotational kinetic energy and translational motion.

Next, test your hypothesis by rolling the cans down a gently inclined plane. Observe any differences in their speeds. Which one rolls the fastest? Which one rolls the slowest?

To explore further, fill identical empty cylindrical cans with different substances such as dry rice, water, peanut butter, or sand. Note how the internal distribution of mass and interaction with the can’s shell affects each can’s rolling behavior. This simple experiment highlights the role of moment of inertia and internal motion in rotational energy conservation.

Calculating the Speed of a Cylinder Rolling Down an Incline

Calculate the final speed of a solid cylinder that rolls down a 2.00-m-high incline. The cylinder starts from rest, has a mass of 0.750 kg, and has a radius of 4.00 cm.

Strategy

We can solve for the final velocity using conservation of energy, but we must first express rotational quantities in terms of translational quantities to end up with [latex]v[/latex] as the only unknown.

Solution

Conservation of energy for this situation is written as described above:

[latex]\text{mgh}=\frac{1}{2}{\mathit{mv}}^{2}+\frac{1}{2}{\mathrm{I\omega }}^{2}.[/latex]

Before we can solve for [latex]v[/latex] , we must get an expression for [latex]I[/latex] from Dynamics of  Rotation Motion: Rotation Inertia- Making Connections. Because [latex]v[/latex] and [latex]\omega[/latex] are related (note here that the cylinder is rolling without slipping), we must also substitute the relationship [latex]\omega =v/R[/latex] into the expression. These substitutions yield

[latex]\text{mgh}=\frac{1}{2}{\mathit{mv}}^{2}+\frac{1}{2}\left(\frac{1}{2}{\mathit{mR}}^{2}\right)\left(\frac{{v}^{2}}{{R}^{2}}\right).[/latex]

Interestingly, the cylinder’s radius [latex]R[/latex] and mass [latex]m[/latex] cancel, yielding

[latex]\text{gh}=\frac{1}{2}{v}^{2}+\frac{1}{4}{v}^{2}=\frac{3}{4}{v}^{2}.[/latex]

Solving algebraically, the equation for the final velocity [latex]v[/latex] gives

[latex]v={\left(\frac{4\text{gh}}{3}\right)}^{1/2}.[/latex]

Substituting known values into the resulting expression yields

[latex]v={\left[\frac{4\left(9.80\phantom{\rule{0.25em}{0ex}}{\text{m/s}}^{2}\right)\left(\text{2.00 m}\right)}{3}\right]}^{1/2}=\text{5.11 m/s}.[/latex]

Discussion

Because [latex]m[/latex] and [latex]R[/latex] cancel, the result [latex]v={\left(\frac{4}{3}\text{gh}\right)}^{1/2}[/latex] is valid for any solid cylinder, implying that all solid cylinders will roll down an incline at the same rate independent of their masses and sizes. (Rolling cylinders down inclines is what Galileo actually did to show that objects fall at the same rate independent of mass.) Note that if the cylinder slid without friction down the incline without rolling, then the entire gravitational potential energy would go into translational kinetic energy. Thus, [latex]\frac{1}{2}{\text{mv}}^{2}=\text{mgh}[/latex] and [latex]v=\left(2\text{gh}\right)^{1/2}[/latex], which is 22% greater than [latex]\left(4\text{gh}/3\right)^{1/2}[/latex]. That is, the cylinder would go faster at the bottom.

Check Your Understanding

Is rotational kinetic energy completely analogous to translational kinetic energy? What are their differences, if any? Provide an example of each type of kinetic energy.

Yes, rotational and translational kinetic energy are direct analogs in physics. Both represent the energy of motion, and both depend on mass and velocity—though in different ways. Translational kinetic energy is associated with motion along a straight or curved path, while rotational kinetic energy is associated with motion around an axis.

The mathematical forms are also analogous:

[latex]{\text{KE}}_{\text{trans}} = \frac{1}{2}mv^2[/latex]
[latex]{\text{KE}}_{\text{rot}} = \frac{1}{2}I\omega^2[/latex]

Here, [latex]m[/latex] is mass, [latex]v[/latex] is linear velocity, [latex]I[/latex] is moment of inertia, and [latex]\omega[/latex] is angular velocity.

Example: Consider a rolling bicycle wheel. As the bicycle moves forward, the wheel exhibits both translational kinetic energy (due to the whole wheel moving forward) and rotational kinetic energy (due to its spinning about the axle). If the wheel is lifted off the ground and spun in place, it only has rotational kinetic energy relative to the ground.

PhET Explorations: My Solar System

Use this interactive simulation to explore the dynamics of orbital motion. Create your own solar system by adjusting the initial positions, velocities, and masses of up to four celestial bodies. Observe how gravity governs their motion and how angular momentum and energy are conserved within the system.

Section Summary

[latex]{\text{KE}}_{\text{rot}} = \frac{1}{2} I \omega^2[/latex]
  • Helicopter blades store significant amounts of rotational kinetic energy, which must be built up prior to takeoff and preserved during flight. The onboard engine does not have sufficient capacity to simultaneously generate lift and restore lost rotational energy if the blades slow down significantly.
  • Work and energy in rotational systems follow the same principles as in translational systems. Torque plays the role of force, and angular displacement substitutes for linear displacement.
  • The work-energy theorem for rotational motion is expressed as:
    [latex]\text{net } W = \frac{1}{2} I \omega^2 - \frac{1}{2} I \omega_0^2[/latex]

Conceptual Questions

  1. Describe the energy transformations involved when a yo-yo is thrown downward and then climbs back up its string to be caught in the user’s hand.
  2. What energy transformations are involved when a dragster engine is revved, its clutch let out rapidly, its tires spun, and it starts to accelerate forward? Describe the source and transformation of energy at each step.
  3. The Earth has more rotational kinetic energy now than did the cloud of gas and dust from which it formed. Where did this energy come from?
    The figure shows a closed view of a red planet in the sky, with a sun like object seen at the far right and the planet shown here being surrounded by circles of gas and dust.
    Figure 71.8 An immense cloud of rotating gas and dust contracted under the influence of gravity to form the Earth and in the process rotational kinetic energy increased. (credit: NASA)

Problems & Exercises

  1. This problem considers energy and work aspects of Example 69.1—use data from that example as needed. (a) Calculate the rotational kinetic energy in the merry-go-round plus child when they have an angular velocity of 20.0 rpm. (b) Using energy considerations, find the number of revolutions the father will have to push to achieve this angular velocity starting from rest. (c) Again, using energy considerations, calculate the force the father must exert to stop the merry-go-round in two revolutions
  2. What is the final velocity of a hoop that rolls without slipping down a 5.00-m-high hill, starting from rest? (a) Calculate the rotational kinetic energy of Earth on its axis. (b) What is the rotational kinetic energy of Earth in its orbit around the Sun?
  3. Calculate the rotational kinetic energy in the motorcycle wheel (Figure 71.6) if its angular velocity is 120 rad/s. Assume M = 12.0 kg, R1 = 0.280 m, and R2 = 0.330 m.
  4. A baseball pitcher throws the ball in a motion where there is rotation of the forearm about the elbow joint as well as other movements. If the linear velocity of the ball relative to the elbow joint is 20.0 m/s at a distance of 0.480 m from the joint and the moment of inertia of the forearm is [latex]\text{0.500 kg}\cdot {\text{m}}^{2}[/latex], what is the rotational kinetic energy of the forearm?
  5. While punting a football, a kicker rotates his leg about the hip joint. The moment of inertia of the leg is [latex]\text{3.75 kg}\cdot {\text{m}}^{2}[/latex] and its rotational kinetic energy is 175 J. (a) What is the angular velocity of the leg? (b) What is the velocity of tip of the punter’s shoe if it is 1.05 m from the hip joint? (c) Explain how the football can be given a velocity greater than the tip of the shoe (necessary for a decent kick distance).
  6. A bus contains a 1500 kg flywheel (a disk that has a 0.600 m radius) and has a total mass of 10,000 kg. (a) Calculate the angular velocity the flywheel must have to contain enough energy to take the bus from rest to a speed of 20.0 m/s, assuming 90.0% of the rotational kinetic energy can be transformed into translational energy. (b) How high a hill can the bus climb with this stored energy and still have a speed of 3.00 m/s at the top of the hill?
  7. A ball with an initial velocity of 8.00 m/s rolls up a hill without slipping. Treating the ball as a spherical shell, calculate the vertical height it reaches. (b) Repeat the calculation for the same ball if it slides up the hill without rolling.
  8. While exercising in a fitness center, a man lies face down on a bench and lifts a weight with one lower leg by contacting the muscles in the back of the upper leg. (a) Find the angular acceleration produced given the mass lifted is 10.0 kg at a distance of 28.0 cm from the knee joint, the moment of inertia of the lower leg is [latex]\text{0.900 kg}\cdot {\text{m}}^{2}[/latex], the muscle force is 1500 N, and its effective perpendicular lever arm is 3.00 cm. (b) How much work is done if the leg rotates through an angle of [latex]\text{20.0º}[/latex] with a constant force exerted by the muscle?
  9. To develop muscle tone, a woman lifts a 2.00-kg weight held in her hand. She uses her biceps muscle to flex the lower arm through an angle of [latex]\text{60.0º}[/latex]. (a) What is the angular acceleration if the weight is 24.0 cm from the elbow joint, her forearm has a moment of inertia of [latex]\text{0.250 kg}\cdot {\text{m}}^{2}[/latex], and the net force she exerts is 750 N at an effective perpendicular lever arm of 2.00 cm? (b) How much work does she do?
  10. Consider two cylinders that start down identical inclines from rest except that one is frictionless. Thus one cylinder rolls without slipping, while the other slides frictionlessly without rolling. They both travel a short distance at the bottom and then start up another incline. (a) Show that they both reach the same height on the other incline, and that this height is equal to their original height. (b) Find the ratio of the time the rolling cylinder takes to reach the height on the second incline to the time the sliding cylinder takes to reach the height on the second incline. (c) Explain why the time for the rolling motion is greater than that for the sliding motion.
  11. What is the moment of inertia of an object that rolls without slipping down a 2.00-m-high incline starting from rest, and has a final velocity of 6.00 m/s? Express the moment of inertia as a multiple of [latex]{\mathit{MR}}^{2}[/latex], where [latex]M[/latex] is the mass of the object and [latex]R[/latex] is its radius.
  12. Suppose a 200-kg motorcycle has two wheels like the one in Figure 69.6 and is heading toward a hill at a speed of 30.0 m/s. (a) How high can it coast up the hill, if you neglect friction? (b) How much energy is lost to friction if the motorcycle only gains an altitude of 35.0 m before coming to rest?
  13. In softball, the pitcher throws with the arm fully extended (straight at the elbow). In a fast pitch the ball leaves the hand with a speed of 139 km/h. (a) Find the rotational kinetic energy of the pitcher’s arm given its moment of inertia is [latex]\text{0.720 kg}\cdot {\text{m}}^{2}[/latex] and the ball leaves the hand at a distance of 0.600 m from the pivot at the shoulder. (b) What force did the muscles exert to cause the arm to rotate if their effective perpendicular lever arm is 4.00 cm and the ball is 0.156 kg?
  14. Construct Your Own Problem Consider the work done by a spinning skater pulling her arms in to increase her rate of spin. Construct a problem in which you calculate the work done with a “force multiplied by distance” calculation and compare it to the skater’s increase in kinetic energy.

Glossary

work-energy theorem
if one or more external forces act upon a rigid object, causing its kinetic energy to change from [latex]{\text{KE}}_{\text{1}}[/latex] to [latex]{\text{KE}}_{\text{2}}[/latex], then the work [latex]W[/latex] done by the net force is equal to the change in kinetic energy
rotational kinetic energy
the kinetic energy due to the rotation of an object. This is part of its total kinetic energy
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book