"

Uniform Circular Motion and Gravitation

35 Rotation Angle and Angular Velocity

Learning Objectives

  • Define arc length, rotation angle, radius of curvature and angular velocity.
  • Calculate the angular velocity of a car wheel spin.

In earlier chapters, we studied Kinematics in straight lines and in two dimensions, like projectile motion. Now we turn to motion along curved paths. Unlike projectiles, which eventually land, we will focus on motion that continues along a curve, such as a CD spinning or a car wheel rotating.

 

Rotation Angle

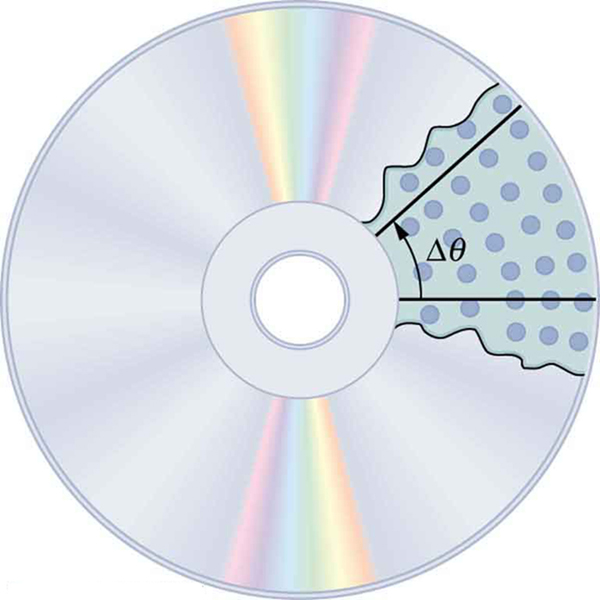
When an object rotates around a fixed axis, every point on it follows a circular path. For example, imagine a compact disc (CD) spinning in a player. Each “pit” on a line from the center to the edge of the disc moves through the same angle at the same time (Figure 35.1). The amount of rotation is called the rotation angle and is similar to measuring a distance traveled but along a curve.

We define the rotation angle [latex]\Delta \theta[/latex] as the ratio of the arc length [latex]\Delta s[/latex] to the radius of curvature [latex]r[/latex]:

[latex]\Delta \theta = \frac{\Delta s}{r}[/latex]

  • [latex]\Delta \theta[/latex] is in radians (rad)

  • [latex]\Delta s[/latex] is the arc length (in meters)

  • [latex]r[/latex] is the radius from the axis of rotation (in meters)

The figure shows the back side of a compact disc. There is a scratched part on the upper right side of the C D, about one-fifth size of the whole area, with inner circular dots clearly visible. Two line segments are drawn enclosing the scratched area from the border of the C D to the middle plastic portion. A curved arrow is drawn between the two line segments near this middle portion and angle delta theta written alongside it.
Figure 35.1: All points on a CD travel in circular arcs. The pits along a line from the center to the edge all move through the same angle [latex]\Delta \theta[/latex] in a time [latex]\Delta t[/latex].

Arc Length and Radians

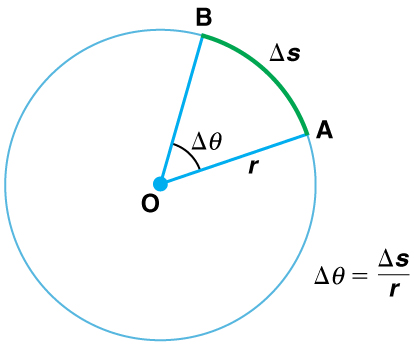
A radian is a unit based on the arc of a circle. One full circle has an arc length of:

[latex]\Delta s = 2\pi r[/latex]

So the total rotation angle for one complete revolution as shown in Figure 35.2 is:

[latex]\Delta \theta = \frac{2\pi r}{r} = 2\pi \text{ radians}[/latex]

This is why:

[latex]2\pi \ \text{rad} = 1 \ \text{revolution} = 360^\circ[/latex]

Thus, we can convert between radians and degrees:

[latex]1 \ \text{rad} = \frac{360^\circ}{2\pi} \approx 57.3^\circ[/latex]

A circle of radius r and center O is shown. A radius O-A of the circle is rotated through angle delta theta about the center O to terminate as radius O-B. The arc length A-B is marked as delta s.
Figure 35.2: A radius of a circle is rotated through an angle [latex]\Delta \theta[/latex]. The arc length [latex]\Delta s[/latex] is the curved path on the circumference. The radius [latex]r[/latex] stays constant.

A comparison of some useful angles expressed in both degrees and radians is shown in Table 35.1

Table 35.1 Comparison of Angular Units
Degree Measures Radian Measure
[latex]\text{30º}[/latex] [latex]\frac{\pi }{6}[/latex]
[latex]\text{60º}[/latex] [latex]\frac{\pi }{3}[/latex]
[latex]\text{90º}[/latex] [latex]\frac{\pi }{2}[/latex]
[latex]\text{120º}[/latex] [latex]\frac{2\pi }{3}[/latex]
[latex]\text{135º}[/latex] [latex]\frac{3\pi }{4}[/latex]
[latex]\text{180º}[/latex] [latex]\pi[/latex]
A circle is shown. Two radii of the circle, inclined at an acute angle delta theta, are shown. On one of the radii, two points, one and two are marked. The point one is inside the circle through which an arc between the two radii is shown. The point two is on the cirumfenrence of the circle. The two arc lengths are delta s one and delta s two respectively for the two points.
Figure 35.3: Points 1 and 2 rotate through the same angle ([latex]\text{Δ}\theta [/latex]), but point 2 moves through a greater arc length [latex]\left(\text{Δ}s\right)[/latex] because it is at a greater distance from the center of rotation [latex]\left(r\right)[/latex].

If [latex]\text{Δ}\theta =2\pi[/latex] rad, then the CD has made one complete revolution, and every point on the CD is back at its original position. Because there are [latex]\text{360º}[/latex] in a circle or one revolution, the relationship between radians and degrees is thus

[latex]2\pi \phantom{\rule{0.25em}{0ex}}\text{rad}=\text{360º}[/latex]

so that

[latex]1\phantom{\rule{0.25em}{0ex}}\text{rad}=\frac{\text{360º}}{2\pi }\approx \text{57.}3º\text{.}[/latex]

Angular Velocity

Just like linear velocity describes how fast an object moves in a straight line, angular velocity describes how fast something is rotating.

The average angular velocity [latex]\omega[/latex] is:

[latex]\omega = \frac{\Delta \theta}{\Delta t}[/latex]

  • Units: radians per second (rad/s)

The larger the rotation angle per time, the faster the angular velocity.

Linear and Angular Velocity Connection

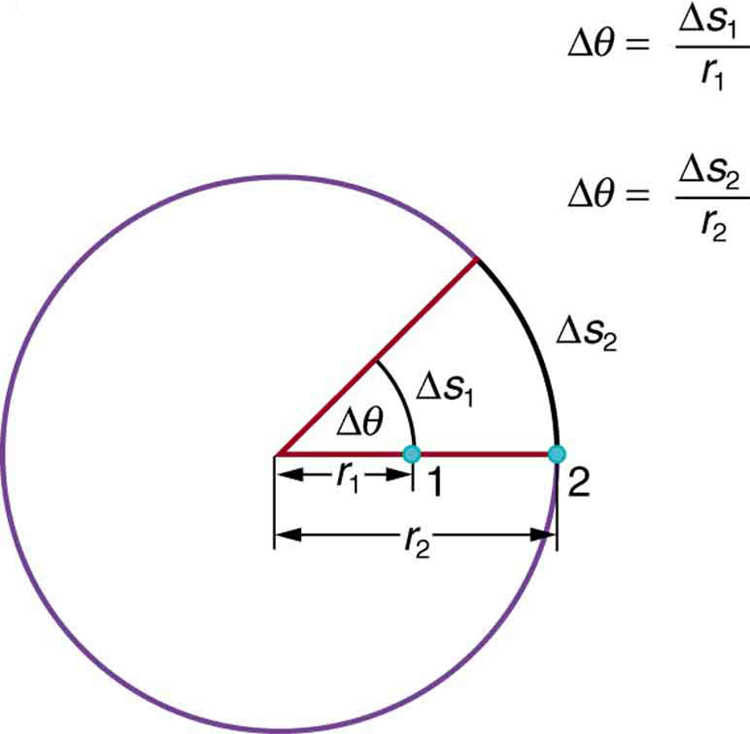
Consider a point on the rim of a spinning CD or the tire of a car. It travels a certain arc length [latex]\Delta s[/latex] in time [latex]\Delta t[/latex], giving it a linear velocity:

[latex]v = \frac{\Delta s}{\Delta t}[/latex]

Since:

[latex]\Delta s = r \Delta \theta[/latex]

Substitute into the formula for linear velocity:

[latex]v = \frac{r \Delta \theta}{\Delta t} = r\omega[/latex]

So we have two equivalent relationships:

[latex]v = r \omega \quad \text{or} \quad \omega = \frac{v}{r}[/latex]

This shows:

  • Tangential (linear) speed [latex]v[/latex] increases with the radius [latex]r[/latex] if [latex]\omega[/latex] is constant.

  • A larger wheel (larger [latex]r[/latex]) spins slower to maintain the same [latex]v[/latex].

  • A faster-spinning wheel (larger [latex]\omega[/latex]) increases linear speed.

The relationship in [latex]v=\mathrm{r\omega }\text{ or }\omega =\frac{v}{r}[/latex] can be illustrated by considering the tire of a moving car. Note that the speed of a point on the rim of the tire is the same as the speed [latex]v[/latex] of the car. See Figure 35.4 So the faster the car moves, the faster the tire spins—large [latex]v[/latex] means a large [latex]\omega[/latex], because [latex]v=\mathrm{r\omega }[/latex]. Similarly, a larger-radius tire rotating at the same angular velocity ([latex]\omega[/latex]) will produce a greater linear speed ([latex]v[/latex]) for the car.

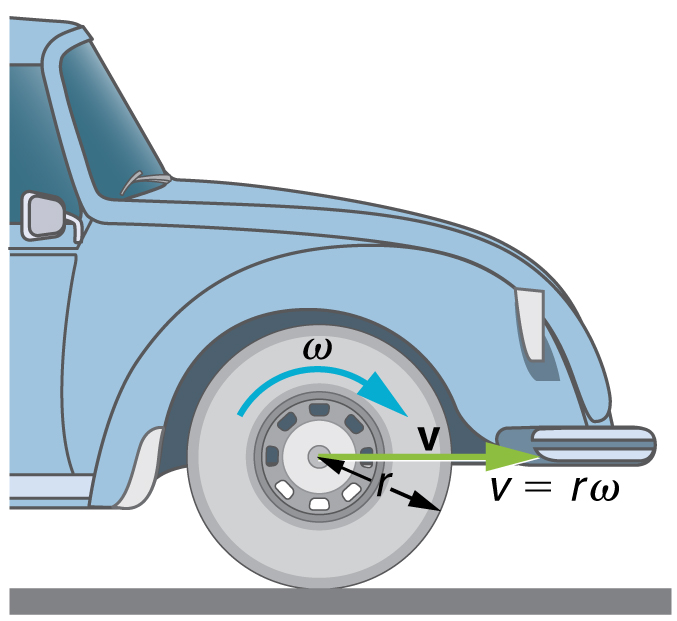
The given figure shows the front wheel of a car. The radius of the car wheel, r, is shown as an arrow and the linear velocity, v, is shown with a green horizontal arrow pointing rightward. The angular velocity, omega, is shown with a clockwise-curved arrow over the wheel.
Figure 35.4: A car moves forward with linear speed [latex]v[/latex] while its wheel rotates with angular velocity [latex]\omega[/latex]. The speed of the wheel’s edge relative to the axle is [latex]v = r\omega[/latex]. A bigger tire at the same spin rate means faster car speed.

Example 35.1: How Fast Does a Car Tire Spin?

Calculate the angular velocity of a 0.300 m radius car tire when the car travels at [latex]\text{15}\text{.}0\phantom{\rule{0.25em}{0ex}}\text{m/s}[/latex] (about [latex]\text{54}\phantom{\rule{0.25em}{0ex}}\text{km/h}[/latex]). See Figure 35.4

Strategy

Because the linear speed of the tire rim is the same as the speed of the car, we have
[latex]v=\text{15.0 m/s}.[/latex]

The radius of the tire is given to be
[latex]r=\text{0.300 m}.[/latex] Knowing

[latex]v[/latex] and [latex]r[/latex], we can use the second relationship in [latex]v=\mathrm{r\omega }\mathrm{, }\omega =\frac{v}{r}[/latex] to calculate the angular velocity.

Solution

To calculate the angular velocity, we will use the following relationship:

[latex]\omega =\frac{v}{r}\text{.}[/latex]

Substituting the knowns,

[latex]\omega =\frac{\text{15}\text{.}0\phantom{\rule{0.25em}{0ex}}\text{m/s}}{0\text{.}\text{300}\phantom{\rule{0.25em}{0ex}}\text{m}}=\text{50}\text{.}0\phantom{\rule{0.25em}{0ex}}\text{rad/s.}[/latex]

Discussion

When we cancel units in the above calculation, we get 50.0/s. But the angular velocity must have units of rad/s. Because radians are actually unitless (radians are defined as a ratio of distance), we can simply insert them into the answer for the angular velocity. Also note that if an earth mover with much larger tires, say 1.20 m in radius, were moving at the same speed of 15.0 m/s, its tires would rotate more slowly. They would have an angular velocity

[latex]\omega =\left(\text{15}\text{.}0\phantom{\rule{0.25em}{0ex}}\text{m/s}\right)/\left(1\text{.}\text{20}\phantom{\rule{0.25em}{0ex}}\text{m}\right)=\text{12}\text{.}5\phantom{\rule{0.25em}{0ex}}\text{rad/s.}[/latex]

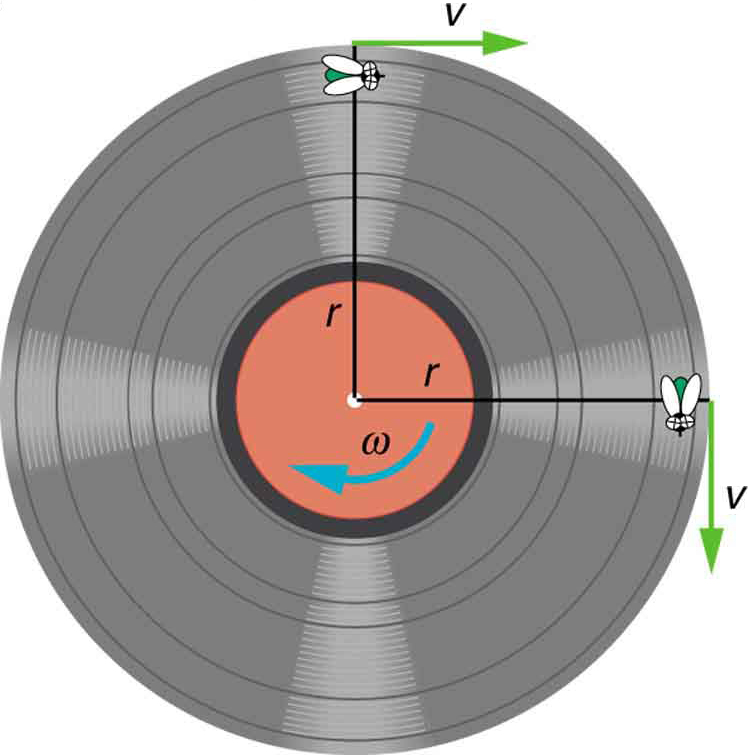
Direction of Angular and Linear Velocity

Just like straight-line motion has direction, rotational motion does too. Both angular velocity [latex]\omega[/latex] and linear velocity [latex]v[/latex] are vector quantities—they have both magnitude and direction.

  • Angular velocity [latex]\omega[/latex] has only two possible directions with respect to the axis of rotation:

    • Clockwise (CW)

    • Counterclockwise (CCW)

  • Linear velocity [latex]v[/latex] is always tangent to the circular path at any point on the rotating object. That’s why it’s also called tangential velocity.

This idea is illustrated in Figure 35.5

The given figure shows the top view of an old fashioned vinyl record. Two perpendicular line segments are drawn through the center of the circular record, one vertically upward and one horizontal to the right side. Two flies are shown at the end points of the vertical lines near the borders of the record. Two arrows are also drawn perpendicularly rightward through the end points of these vertical lines depicting linear velocities. A curved arrow is also drawn at the center circular part of the record which shows the angular velocity.
Figure 35.5: As an object moves in a circular path—like a fly sitting on the edge of an old vinyl record—its instantaneous velocity is always tangent to the circle. The angular velocity vector points clockwise in this example, since the record spins in that direction.

🧪 Take-Home Experiment: Measuring Angular and Linear Speed

Try this hands-on activity to connect theory with real-world motion:

  1. Materials Needed:

    • A small object (e.g., a key or small ball)

    • A string about 1 meter long

    • A stopwatch or timer

  2. What to Do:

    • Tie the object to one end of the string.

    • Swing it in a horizontal circle above your head by rotating your wrist.

    • Try to maintain a steady (uniform) speed as it spins.

  3. Measure Angular Velocity:

    • Count how many full revolutions the object makes in, say, 10 seconds.

    • Angular velocity is:
      [latex]\omega = \frac{2\pi \times \text{(number of revolutions)}}{\text{time}} \ (\text{rad/s})[/latex]

  4. Estimate Linear Speed:

    • Measure the length of the string (this is [latex]r[/latex]).

    • Use the formula:
      [latex]v = r\omega[/latex]

  5. Try Measuring Closer In:

    • Choose a point closer to your hand (shorter radius) and repeat.

    • Notice that even with the same [latex]\omega[/latex], the linear speed [latex]v[/latex] is smaller.

  6. Explore More:

    • Look around for other rotating objects—fans, wheels, turntables.

    • Estimate or measure their angular velocities using this same method!

This experiment is a simple way to see the difference between angular and linear velocity and how they relate. It also connects to biological applications like joint motion in limbs or the motion of circular cellular structures like cilia and flagella.

PhET Explorations: Ladybug Revolution

Explore the fascinating world of rotational motion with the interactive PhET simulation Ladybug Revolution. In this simulation, a ladybug sits on a merry-go-round, and you control the motion!

What You Can Do:

  • Manually rotate the merry-go-round to observe how angular position changes.

  • Set a constant angular velocity or apply an angular acceleration.

  • Visualize how circular motion relates to:

    • The ladybug’s x and y position

    • Velocity and acceleration vectors

    • Graphical representations of motion

Key Concepts Explored:

  • Angular position, velocity, and acceleration

  • Relationship between rotational and linear quantities

  • Motion in two dimensions on a rotating frame

This tool helps reinforce concepts like [latex]\omega[/latex], [latex]\alpha[/latex], and tangential versus radial acceleration. It’s a great way to build intuition for rotational motion through direct manipulation and real-time feedback.

 

Section Summary

  • Uniform circular motion refers to motion along a circular path with constant speed.

  • The rotation angle [latex]\Delta\theta[/latex] quantifies how much an object rotates and is defined as the ratio of arc length to the radius of curvature:

    [latex]\Delta\theta = \frac{\Delta s}{r}[/latex]

    where:

    • [latex]\Delta s[/latex] is the arc length (the linear distance traveled along the circular path),

    • [latex]r[/latex] is the radius of the circular path.

  • The rotation angle [latex]\Delta\theta[/latex] is measured in radians (rad), where:

    [latex]2\pi\ \text{rad} = 360^\circ = 1\ \text{revolution}[/latex]

    Thus, the conversion between radians and degrees is:

    [latex]1\ \text{rad} \approx 57.3^\circ[/latex]

  • Angular velocity [latex]\omega[/latex] is the rate of change of the rotation angle over time:

    [latex]\omega = \frac{\Delta\theta}{\Delta t}[/latex]

    where [latex]\Delta t[/latex] is the elapsed time. Angular velocity is measured in radians per second (rad/s).

  • The linear velocity [latex]v[/latex] of an object in circular motion is directly related to its angular velocity [latex]\omega[/latex] and the radius [latex]r[/latex] of the circular path:

    [latex]v = r\omega \quad \text{or} \quad \omega = \frac{v}{r}[/latex]

    This means that for a given angular velocity, points farther from the axis of rotation move faster in a straight line.

Conceptual Questions

  1. There is an analogy between rotational and linear physical quantities. What rotational quantities are analogous to distance and velocity?

Problem Exercises

  1. Semi-trailer trucks have an odometer on one hub of a trailer wheel. The hub is weighted so that it does not rotate, but it contains gears to count the number of wheel revolutions—it then calculates the distance traveled. If the wheel has a 1.15 m diameter and goes through 200,000 rotations, how many kilometers should the odometer read?
  2. Microwave ovens rotate at a rate of about 6 rev/min. What is this in revolutions per second? What is the angular velocity in radians per second?
  3. An automobile with 0.260 m radius tires travels 80,000 km before wearing them out. How many revolutions do the tires make, neglecting any backing up and any change in radius due to wear?
  4. (a) What is the period of rotation of Earth in seconds? (b) What is the angular velocity of Earth? (c) Given that Earth has a radius of [latex]6\text{.}4×{\text{10}}^{6}\phantom{\rule{0.25em}{0ex}}\text{m}[/latex] at its equator, what is the linear velocity at Earth’s surface?
  5. A baseball pitcher brings his arm forward during a pitch, rotating the forearm about the elbow. If the velocity of the ball in the pitcher’s hand is 35.0 m/s and the ball is 0.300 m from the elbow joint, what is the angular velocity of the forearm?
  6. In lacrosse, a ball is thrown from a net on the end of a stick by rotating the stick and forearm about the elbow. If the angular velocity of the ball about the elbow joint is 30.0 rad/s and the ball is 1.30 m from the elbow joint, what is the velocity of the ball?
  7. A truck with 0.420-m-radius tires travels at 32.0 m/s. What is the angular velocity of the rotating tires in radians per second? What is this in rev/min?
  8. Integrated Concepts When kicking a football, the kicker rotates his leg about the hip joint.
    1. If the velocity of the tip of the kicker’s shoe is 35.0 m/s and the hip joint is 1.05 m from the tip of the shoe, what is the shoe tip’s angular velocity?
    2. The shoe is in contact with the initially stationary 0.500 kg football for 20.0 ms. What average force is exerted on the football to give it a velocity of 20.0 m/s?
    3. Find the maximum range of the football, neglecting air resistance.
  9. Construct Your Own Problem Consider an amusement park ride in which participants are rotated about a vertical axis in a cylinder with vertical walls. Once the angular velocity reaches its full value, the floor drops away and friction between the walls and the riders prevents them from sliding down. Construct a problem in which you calculate the necessary angular velocity that assures the riders will not slide down the wall. Include a free body diagram of a single rider. Among the variables to consider are the radius of the cylinder and the coefficients of friction between the riders’ clothing and the wall.

Glossary

arc length
[latex]\text{Δ}s[/latex], the distance traveled by an object along a circular path
pit
a tiny indentation on the spiral track moulded into the top of the polycarbonate layer of CD
rotation angle
the ratio of the arc length to the radius of curvature on a circular path:

[latex]\text{Δ}\theta =\frac{\text{Δ}s}{r}[/latex]

radius of curvature
radius of a circular path
radians
a unit of angle measurement
angular velocity
[latex]\omega[/latex], the rate of change of the angle with which an object moves on a circular path
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book