"

Fluid Statics

83 Pressures in the Body

Learning Objectives

  • Explain the concept of pressure in the human body.
  • Define systolic and diastolic blood pressure.
  • Describe fluid pressures in the eye, lungs, spinal column, bladder, and skeletal system, and explain their medical significance.

Pressure in the Body

Aside from measuring temperature and weight, assessing a patient’s blood pressure is one of the most routine diagnostic practices in medicine. Hypertension (chronic high blood pressure) is a major risk factor for stroke, heart failure, and kidney disease. Monitoring pressure in various body systems provides essential information about health status and helps guide treatment decisions.

Table 83.1 summarizes typical gauge pressures measured in different regions of the human body, expressed in millimeters of mercury (mm Hg).

Table 83.1 Typical Pressures in Humans
Body system Gauge pressure in mm Hg
Blood pressures in large arteries (resting)
Maximum (systolic) 100–140
Minimum (diastolic) 60–90
Blood pressure in large veins 4–15
Eye 12–24
Brain and spinal fluid (lying down) 5–12
Bladder
While filling 0–25
When full 100–150
Chest cavity between lungs and ribs −8 to −4
Inside lungs −2 to +3
Digestive tract
Esophagus −2
Stomach 0–20
Intestines 10–20
Middle ear <1

Blood Pressure and Circulatory Physiology

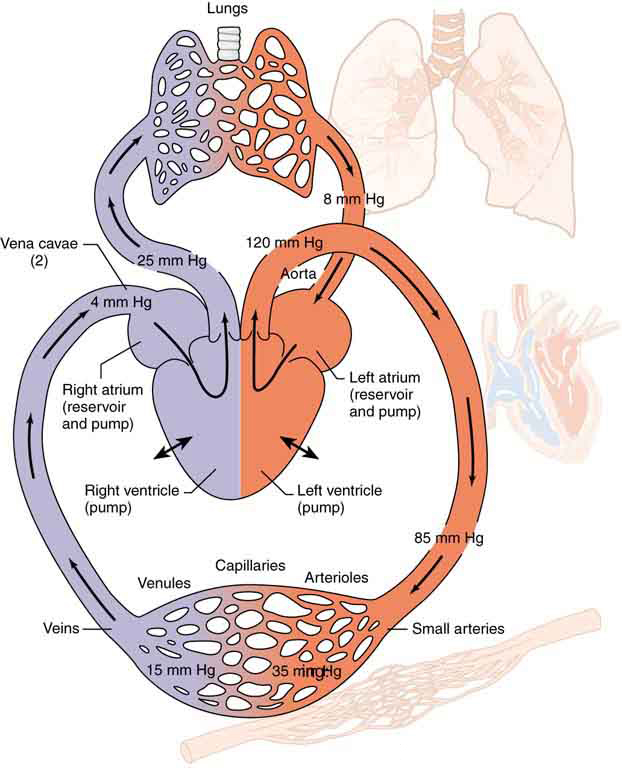
The standard blood pressure reading—typically 120/80 mm Hg—represents the systolic and diastolic pressures. Systolic pressure reflects the force exerted by the heart during contraction, while diastolic pressure reflects the residual pressure when the heart relaxes. Both values are crucial for assessing cardiovascular health. High systolic pressure can damage arteries and increase stroke risk; elevated diastolic pressure may indicate inadequate vessel relaxation or excess fluid volume.

During vigorous exercise, systolic pressure can rise significantly to support increased perfusion, returning to normal afterward. In contrast, diastolic pressure remains relatively stable; deviations may indicate underlying pathology such as hemorrhage or fluid overload.

Pressure in the circulatory system decreases progressively as blood travels from the aorta through arterioles, capillaries, venules, and veins. This is due to both resistance and vertical positioning. For example, in a standing person, gravity increases the blood pressure in the feet relative to the heart. Using the hydrostatic pressure formula:

[latex]\Delta P = \rho g h = (1050 \, \text{kg/m}^3)(9.80 \, \text{m/s}^2)(1.4 \, \text{m}) = 1.4 \times 10^4 \, \text{Pa} \approx 108 \, \text{mm Hg}[/latex]

This explains why standing for prolonged periods can lead to blood pooling and edema in the lower limbs. Compression garments, such as compression stockings, help counteract this by exerting external pressure to assist venous return.

More invasive blood pressure measurements—such as within heart chambers or pulmonary arteries—require catheterization and are typically performed in critical care or surgical settings.

Right vs. Left Heart Failure

The heart acts as a dual pump (Figure 83.1). The right heart circulates blood through the pulmonary system; the left heart propels blood into systemic circulation. In right-heart failure, blood backs up in the vena cavae, increasing venous pressure. In left-heart failure, pressure builds upstream in the pulmonary veins, potentially causing pulmonary edema.

The figure shows the circulatory system in the human body. The figure shows the right atrium and the left atrium, right ventricle and the left ventricle of the heart. The heart consists of two pumps—the right side forcing blood through the lungs and the left causing blood to flow through the rest of the body.
Figure 83.1 Pressures in the human circulatory system. The heart’s two pumps generate the pressure required to circulate blood through both pulmonary and systemic circuits. Long-term deviations can indicate pathological conditions.

Pressure in the Eye

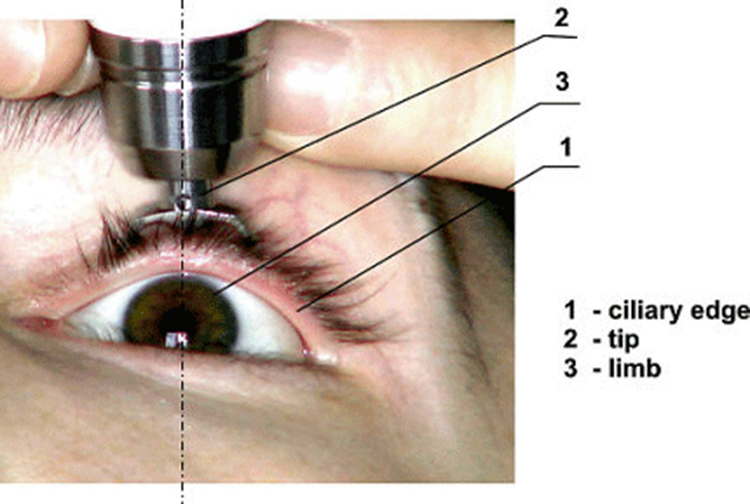
The spherical shape of the eye is maintained by intraocular pressure—fluid pressure exerted by the aqueous humor. Normal values range from 12 to 24 mm Hg. A blockage in fluid drainage leads to increased pressure, a condition known as glaucoma, which can damage the optic nerve and result in vision loss.

Suppose intraocular pressure rises to 85 mm Hg and acts over an area of [latex]6.0 \, \text{cm}^2[/latex] on the back of the eye. Converting to SI units:

[latex]F = \rho g h A = (13.6 \times 10^3 \, \text{kg/m}^3)(9.80 \, \text{m/s}^2)(85.0 \times 10^{-3} \, \text{m})(6.0 \times 10^{-4} \, \text{m}^2) = 6.8 \, \text{N}[/latex]

This is roughly equivalent to the force exerted by a 680-g mass—enough to cause structural damage if persistent.

Tonometry is the standard method to assess intraocular pressure. Non-contact tonometers use a puff of air to measure how much the cornea deforms. Higher pressures result in smaller deformations and quicker rebounds (Figure 83.2).

The tonometer being used by an eye care professional to determine the fluid pressure inside the eye.
Figure 83.2 A tonometer measures intraocular pressure by gauging the eye’s resistance to deformation from a small air puff. This is a noninvasive and commonly used test to detect glaucoma risk. (Credit: DevelopAll, Wikipedia Project)

Example 83.1 Calculating Gauge Pressure and Depth: Damage to the Eardrum

Suppose a 3.00-N force can rupture an eardrum. (a) If the eardrum has an area of [latex]1\text{.}\text{00}\phantom{\rule{0.25em}{0ex}}{\text{cm}}^{2}[/latex], calculate the maximum tolerable gauge pressure on the eardrum in newtons per meter squared and convert it to millimeters of mercury. (b) At what depth in freshwater would this person’s eardrum rupture, assuming the gauge pressure in the middle ear is zero?

Strategy for (a)

The pressure can be found directly from its definition since we know the force and area. We are looking for the gauge pressure.

Solution for (a)

[latex]{P}_{\text{g}}=F/A=3\text{.}\text{00}\phantom{\rule{0.25em}{0ex}}\text{N}/\left(1\text{.}\text{00}×{\text{10}}^{-4}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{2}\right)=3\text{.}\text{00}×{\text{10}}^{4}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}.[/latex]

We now need to convert this to units of mm Hg:

[latex]{P}_{\text{g}}=3\text{.}0×{\text{10}}^{4}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}\left(\frac{1.0 mm Hg}{\text{133}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}}\right)=\text{226 mm Hg.}[/latex]

Strategy for (b)

Here we will use the fact that the water pressure varies linearly with depth [latex]h[/latex] below the surface.

Solution for (b)

[latex]P=\mathrm{h\rho g}[/latex] and therefore [latex]h=P/\mathrm{\rho g}[/latex]. Using the value above for [latex]P[/latex], we have

[latex]h=\frac{3.0×{\text{10}}^{4}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}}{\left(1.00×{\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}{\text{kg/m}}^{3}\right)\left(9.80 m{\text{/s}}^{2}\right)}=3.06 m.[/latex]

Discussion

Similarly, increased pressure exerted upon the eardrum from the middle ear can arise when an infection causes a fluid buildup.

Pressure Associated with the Lungs

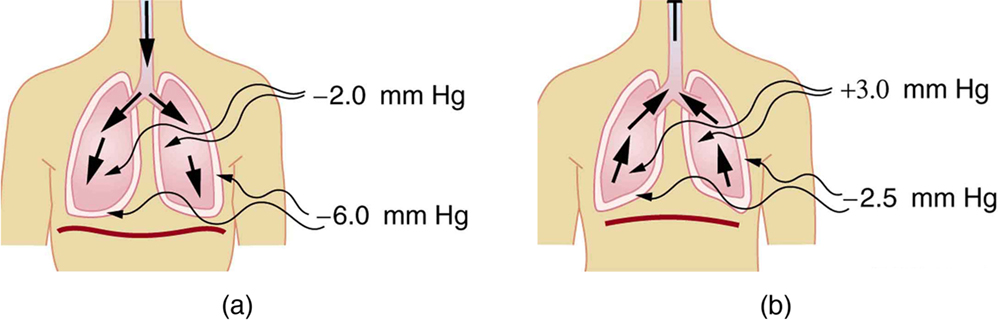
The pressure in the lungs varies with the breathing cycle. During inhalation, expansion of the chest cavity by the diaphragm and intercostal muscles increases lung volume, which decreases pressure below atmospheric levels (a negative gauge pressure). This causes air to flow into the lungs. During exhalation, the lung volume decreases, and pressure increases above atmospheric, forcing air out.

The ability to breathe depends on both muscular effort and the physical properties of lung tissue. Inhalation requires active muscle contraction, which increases the thoracic cavity volume and reduces pressure inside the lungs (Figure 83.3). Exhalation is normally passive, driven by the surface tension in the alveoli, which creates positive pressure that expels air. Forced exhalation—such as during coughing or blowing—requires muscular effort to further increase pressure.

Without mechanical attachment to the chest wall, the lungs would collapse due to alveolar surface tension. This attachment is maintained by a thin layer of pleural fluid, which adheres the lungs to the thoracic cavity through adhesive forces. The pressure in this pleural space is negative, typically ranging from:

[latex]-8 \, \text{mm Hg (inhalation)} \quad \text{to} \quad -4 \, \text{mm Hg (exhalation)}[/latex]

If air enters this space (e.g., due to trauma or surgery), it disrupts the adhesive bond and can cause the lung to collapse—a condition known as pneumothorax. Restoration of negative pressure via suction helps re-inflate the lung.

The figures represent the inhalation and expiration process in the human body. It shows the working of the various muscles and the movement of the diaphragm that causes the variation in the pressure inside the lungs.
Figure 83.3 (a) Inhalation: Muscles expand the chest, diaphragm moves downward, and lung pressure falls below atmospheric. (b) Exhalation: Muscles relax, and alveolar surface tension creates positive pressure to expel air. In both cases, pleural pressure remains negative, anchoring the lungs to the chest wall.

Other Pressures in the Body

Spinal Column and Skull

The brain and spinal cord are surrounded by cerebrospinal fluid (CSF), which exerts a pressure between 5 and 12 mm Hg in a healthy individual. CSF serves multiple purposes—one of the most critical being to provide buoyant support to the brain. Because the brain and CSF have similar densities, the upward force nearly cancels the weight of the brain, preventing it from compressing against the skull.

Loss of CSF—for example, after a lumbar puncture or due to leakage—can cause severe headaches and neurological complications. CSF pressure is typically measured by inserting a needle between lumbar vertebrae (a procedure known as a spinal tap) and reading the pressure via a manometer.

Bladder Pressure

The pressure in the bladder increases gradually as it fills, typically reaching 25 mm Hg at a volume of around [latex]500 \, \text{cm}^3[/latex]. This activates the micturition reflex, which produces the sensation of needing to urinate. Once triggered, muscular contraction raises pressure further—often over 100 mm Hg—to assist urination.

Various external stimuli (e.g., cold, tight clothing, nervousness) and physiological conditions (e.g., pregnancy) can increase bladder pressure and trigger urination urgency. Elevated bladder pressure, especially due to blockage or neurological dysfunction, can result in urine reflux into the kidneys, potentially causing damage. Measurement can be performed via catheterization or direct needle insertion.

Pressures in the Skeletal System

The highest pressures in the body occur in joints and the spinal column, due to large forces acting over small areas. For example, lifting an object improperly may generate a compressive force of 5000 N between two vertebrae. If this force is distributed over an area of only [latex]10 \, \text{cm}^2 = 10^{-3} \, \text{m}^2[/latex], the resulting pressure is:

[latex]P = \frac{F}{A} = \frac{5000 \, \text{N}}{1.0 \times 10^{-3} \, \text{m}^2} = 5.0 \times 10^6 \, \text{N/m}^2 = 50 \, \text{atm}[/latex]

This enormous pressure can damage both intervertebral discs and bone tissue. Even normal activities generate several atmospheres of pressure in the spine. Proper lifting techniques and avoidance of excessive loads are essential to prevent injury. (See Forces and Torques in Muscles and Joints for details.)

Other Physiological Pressures

Additional pressures in the body serve critical biological functions:

  • Digestive tract: Pressure gradients help propel food and waste. The stomach builds up positive pressure as it fills, while the esophagus maintains slightly negative pressure due to the chest cavity’s negative pressure.
  • Heartburn: If gastric pressure exceeds esophageal pressure, acid reflux into the esophagus can occur.
  • Middle ear: Differences between internal and external pressure (such as during flights or diving) exert force on the eardrum, causing discomfort or damage. The Eustachian tubes allow pressure equalization with the throat.

Many of these pressures are intimately related to fluid movement. This topic is explored in greater detail in Fluid Dynamics and Its Biological and Medical Applications.

Section Summary

  • Blood pressure is routinely monitored and is vital to assessing cardiovascular health.
  • Fluid pressures throughout the body—including in the lungs, eye, bladder, and spinal column—are critical for proper function and can indicate pathology.
  • The highest bodily pressures occur in the skeletal system due to force concentration in joints and vertebrae.
  • Glaucoma, pneumothorax, acid reflux, and spinal injuries are all conditions related to abnormal pressures in body compartments.

Problems & Exercises

  1. During forced exhalation, such as when blowing up a balloon, the diaphragm and chest muscles create a pressure of 60.0 mm Hg between the lungs and chest wall. What force in newtons does this pressure create on the [latex]\text{600}\phantom{\rule{0.25em}{0ex}}{\text{cm}}^{2}[/latex] surface area of the diaphragm?
  2. You can chew through very tough objects with your incisors because they exert a large force on the small area of a pointed tooth. What pressure in pascals can you create by exerting a force of [latex]\text{500 N}[/latex] with your tooth on an area of [latex]1.00\phantom{\rule{0.25em}{0ex}}{\text{mm}}^{2}[/latex]?
  3. One way to force air into an unconscious person’s lungs is to squeeze on a balloon appropriately connected to the subject. What force must you exert on the balloon with your hands to create a gauge pressure of 4.00 cm water, assuming you squeeze on an effective area of [latex]\text{50}\text{.}0\phantom{\rule{0.25em}{0ex}}{\text{cm}}^{2}[/latex]?
  4. Heroes in movies hide beneath water and breathe through a hollow reed (villains never catch on to this trick). In practice, you cannot inhale in this manner if your lungs are more than 60.0 cm below the surface. What is the maximum negative gauge pressure you can create in your lungs on dry land, assuming you can achieve [latex]-3.00 cm[/latex] water pressure with your lungs 60.0 cm below the surface?
  5. Gauge pressure in the fluid surrounding an infant’s brain may rise as high as 85.0 mm Hg (5 to 12 mm Hg is normal), creating an outward force large enough to make the skull grow abnormally large. (a) Calculate this outward force in newtons on each side of an infant’s skull if the effective area of each side is [latex]\text{70}\text{.}0\phantom{\rule{0.25em}{0ex}}{\text{cm}}^{2}[/latex]. (b) What is the net force acting on the skull?
  6. A full-term fetus typically has a mass of 3.50 kg. (a) What pressure does the weight of such a fetus create if it rests on the mother’s bladder, supported on an area of [latex]\text{90}\text{.}0\phantom{\rule{0.25em}{0ex}}{\text{cm}}^{2}[/latex]? (b) Convert this pressure to millimeters of mercury and determine if it alone is great enough to trigger the micturition reflex (it will add to any pressure already existing in the bladder).
  7. If the pressure in the esophagus is [latex]-2.00 mm Hg[/latex] while that in the stomach is [latex]+\text{20.0 mm Hg}[/latex], to what height could stomach fluid rise in the esophagus, assuming a density of 1.10 g/mL? (This movement will not occur if the muscle closing the lower end of the esophagus is working properly.)
  8. Pressure in the spinal fluid is measured as shown in Figure 83.4. If the pressure in the spinal fluid is 10.0 mm Hg: (a) What is the reading of the water manometer in cm water? (b) What is the reading if the person sits up, placing the top of the fluid 60 cm above the tap? The fluid density is 1.05 g/mL.
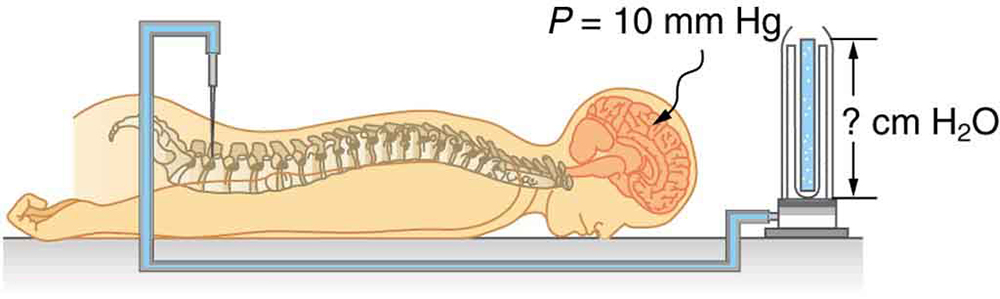
    Diagram of a person lying face-down on a table hooked up to a medical apparatus. A needle attached to a tube is inserted between the patient’s vertebrae in the lower back area. The tube, which appears to be filled with fluid, is connected to an upright tube containing an unknown amount of water. The height of the water in the tube is labeled question-mark centimeters H 2 O. A label pointing to the patient’s head reads P equals ten millimeters H g.
    Figure 83.4 A water manometer used to measure pressure in the spinal fluid. The height of the fluid in the manometer is measured relative to the spinal column, and the manometer is open to the atmosphere. The measured pressure will be considerably greater if the person sits up.
  9. Calculate the maximum force in newtons exerted by the blood on an aneurysm, or ballooning, in a major artery, given the maximum blood pressure for this person is 150 mm Hg and the effective area of the aneurysm is [latex]\text{20}\text{.}0\phantom{\rule{0.25em}{0ex}}{\text{cm}}^{2}[/latex]. Note that this force is great enough to cause further enlargement and subsequently greater force on the ever-thinner vessel wall.
  10. During heavy lifting, a disk between spinal vertebrae is subjected to a 5000-N compressional force. (a) What pressure is created, assuming that the disk has a uniform circular cross section 2.00 cm in radius? (b) What deformation is produced if the disk is 0.800 cm thick and has a Young’s modulus of [latex]1\text{.}5×{\text{10}}^{9}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}[/latex]?
  11. When a person sits erect, increasing the vertical position of their brain by 36.0 cm, the heart must continue to pump blood to the brain at the same rate. (a) What is the gain in gravitational potential energy for 100 mL of blood raised 36.0 cm? (b) What is the drop in pressure, neglecting any losses due to friction? (c) Discuss how the gain in gravitational potential energy and the decrease in pressure are related.
  12. (a) How high will water rise in a glass capillary tube with a 0.500-mm radius? (b) How much gravitational potential energy does the water gain? (c) Discuss possible sources of this energy.
  13. A negative pressure of 25.0 atm can sometimes be achieved with the device in Figure 83.5 before the water separates. (a) To what height could such a negative gauge pressure raise water? (b) How much would a steel wire of the same diameter and length as this capillary stretch if suspended from above?
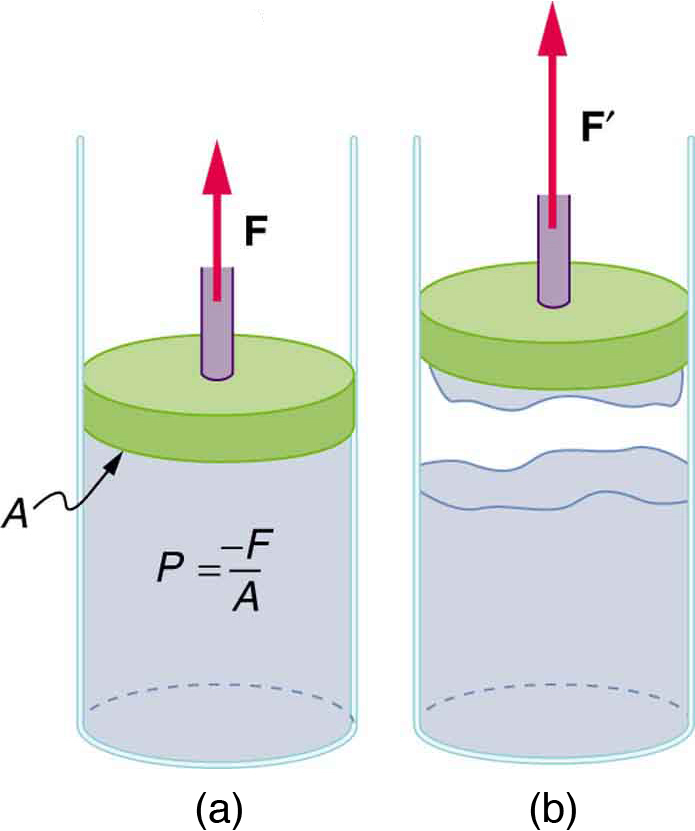
    When the piston is raised the liquid separates and results in negative pressure.
    Figure 83.5 (a) When the piston is raised, it stretches the liquid slightly, putting it under tension and creating a negative absolute pressure [latex]P=-F/A[/latex] (b) The liquid eventually separates, giving an experimental limit to negative pressure in this liquid.
  14. Suppose you hit a steel nail with a 0.500-kg hammer, initially moving at [latex]\text{15.0 m/s}[/latex] and brought to rest in 2.80 mm. (a) What average force is exerted on the nail? (b) How much is the nail compressed if it is 2.50 mm in diameter and 6.00-cm long? (c) What pressure is created on the 1.00-mm-diameter tip of the nail?
  15. Calculate the pressure due to the ocean at the bottom of the Marianas Trench near the Philippines, given its depth is [latex]\text{11.0 km}[/latex] and assuming the density of sea water is constant all the way down. (b) Calculate the percent decrease in volume of sea water due to such a pressure, assuming its bulk modulus is the same as water and is constant. (c) What would be the percent increase in its density? Is the assumption of constant density valid? Will the actual pressure be greater or smaller than that calculated under this assumption?
  16. The hydraulic system of a backhoe is used to lift a load as shown in Figure 83.6. (a) Calculate the force [latex]F[/latex] the slave cylinder must exert to support the 400-kg load and the 150-kg brace and shovel. (b) What is the pressure in the hydraulic fluid if the slave cylinder is 2.50 cm in diameter? (c) What force would you have to exert on a lever with a mechanical advantage of 5.00 acting on a master cylinder 0.800 cm in diameter to create this pressure?
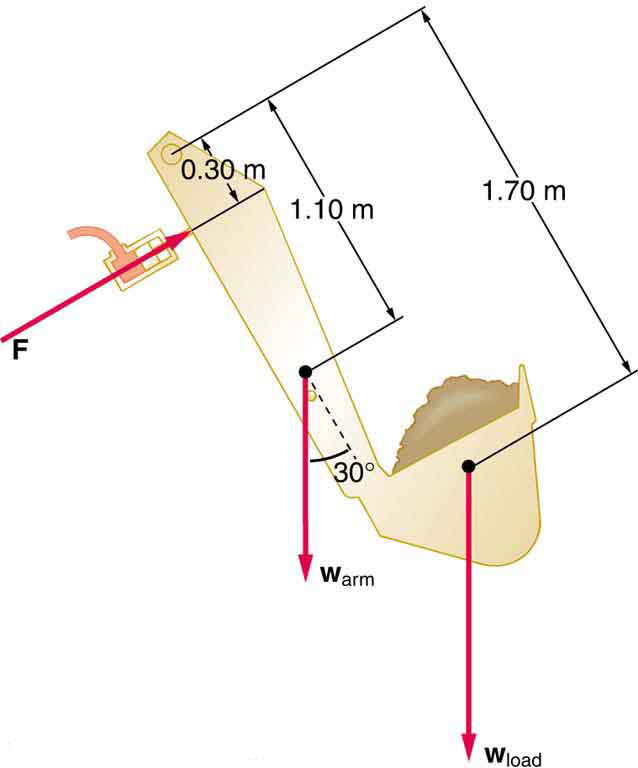
    Diagram of the arm and shovel of a backhoe lifting a load of dirt. The weight of the arm, w sub arm, is depicted as a vector extending vertically downward from the arm one point one zero meters from the top of the arm; w sub arm forms a thirty degree angle with the arm of the shovel. The weight of the load, w sub load, is depicted as a vector extending downward from the middle of the shovel one point seven zero meters from the top of the arm. Force F is a vector pushing the arm of the shovel zero point three zero meters from the top of the arm and perpendicular to the arm.
    Figure 83.6 Hydraulic and mechanical lever systems are used in heavy machinery such as this back hoe.
  17. Some miners wish to remove water from a mine shaft. A pipe is lowered to the water 90 m below, and a negative pressure is applied to raise the water. (a) Calculate the pressure needed to raise the water. (b) What is unreasonable about this pressure? (c) What is unreasonable about the premise?
  18. You are pumping up a bicycle tire with a hand pump, the piston of which has a 2.00-cm radius. (a) What force in newtons must you exert to create a pressure of [latex]6\text{.}\text{90}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{Pa}[/latex] (b) What is unreasonable about this (a) result? (c) Which premises are unreasonable or inconsistent?
  19. Consider a group of people trying to stay afloat after their boat strikes a log in a lake. Construct a problem in which you calculate the number of people that can cling to the log and keep their heads out of the water. Among the variables to be considered are the size and density of the log, and what is needed to keep a person’s head and arms above water without swimming or treading water.
  20. The alveoli in emphysema victims are damaged and effectively form larger sacs. Construct a problem in which you calculate the loss of pressure due to surface tension in the alveoli because of their larger average diameters. (Part of the lung’s ability to expel air results from pressure created by surface tension in the alveoli.) Among the things to consider are the normal surface tension of the fluid lining the alveoli, the average alveolar radius in normal individuals and its average in emphysema sufferers.

Glossary

diastolic pressure
minimum arterial blood pressure; indicator for the fluid balance
glaucoma
condition caused by the buildup of fluid pressure in the eye
intraocular pressure
fluid pressure in the eye
micturition reflex
stimulates the feeling of needing to urinate, triggered by bladder pressure
systolic pressure
maximum arterial blood pressure; indicator for the blood flow
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book