In fluid mechanics, pressure is defined as force per unit area. This definition explains how pressure can be increased by applying a force directly to a fluid—especially when the fluid is enclosed. For example, when the heart contracts, it increases blood pressure by pushing against the blood within the closed circulatory system. In contrast, fluids in open systems, like rivers, escape when compressed. But in enclosed systems—like blood vessels or hydraulic machines—the pressure cannot escape, making it easier to transmit or amplify forces.

In a closed fluid system, pressure is transmitted throughout the entire fluid. Because fluids are composed of freely moving molecules, any change in pressure is instantly communicated in all directions. This phenomenon is known as Pascal’s principle, named after Blaise Pascal:

Pascal’s principle is a foundational idea in fluid mechanics and plays an important role in both engineering and biological systems. It explains, for example, how hydraulic lifts in hospitals raise patient beds and how pressure cuffs measure blood pressure. Most importantly, it allows us to understand that total pressure in a fluid is the sum of the pressures from multiple sources—including both fluid weight and any external forces.

Blaise Pascal (1623–1662), the principle’s namesake, was a self-taught mathematician who made major contributions to number theory and probability. He also invented one of the first mechanical calculators and studied how fluids behave under pressure, laying the groundwork for many medical technologies used today.

Applications in Hydraulic Systems

One of the most practical applications of Pascal’s principle is the hydraulic system, which uses an enclosed fluid to transmit force. In medicine, hydraulics appear in devices like patient lifts, surgical tables, and even some dental chairs. In engineering, they are found in car brakes and heavy machinery. The basic concept of a hydraulic system is illustrated in Figure 79.1.

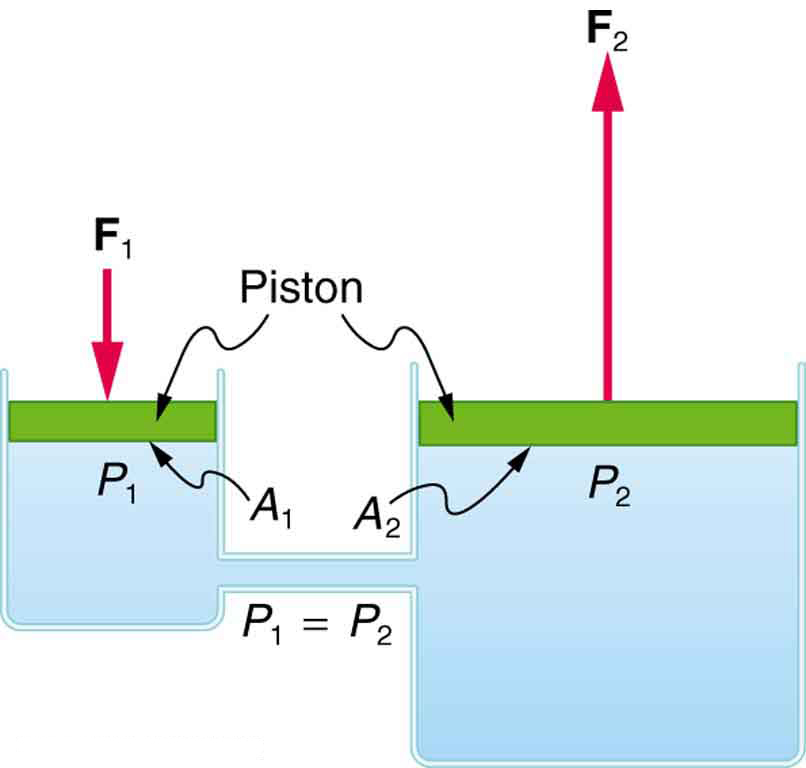
Deriving the Force Relationship in a Hydraulic System

We can derive the relationship between forces in a hydraulic system using Pascal’s principle. Consider two connected cylinders filled with an incompressible fluid. Suppose a force [latex]F_1[/latex] is applied to a small piston of area [latex]A_1[/latex], generating pressure:

According to Pascal’s principle, this pressure is transmitted throughout the fluid, so the pressure at a second piston is also:

Since pressure is force per area, the force at the second piston is:

Equating the two expressions gives:

This equation shows that a small force applied to a small area can be transformed into a much larger force if applied over a larger area. For instance, if [latex]A_2[/latex] is five times greater than [latex]A_1[/latex], the output force [latex]F_2[/latex] will be five times larger than [latex]F_1[/latex].

This mechanical advantage is similar to that of a lever. However, a hydraulic system has the added benefit of being able to transmit force through flexible tubing and around obstacles—allowing for compact and efficient design in both industrial and medical equipment.

Example 79.1 Calculating Force of Slave Cylinders: Pascal Puts on the Brakes

Consider the automobile hydraulic system shown in Figure 79.2.

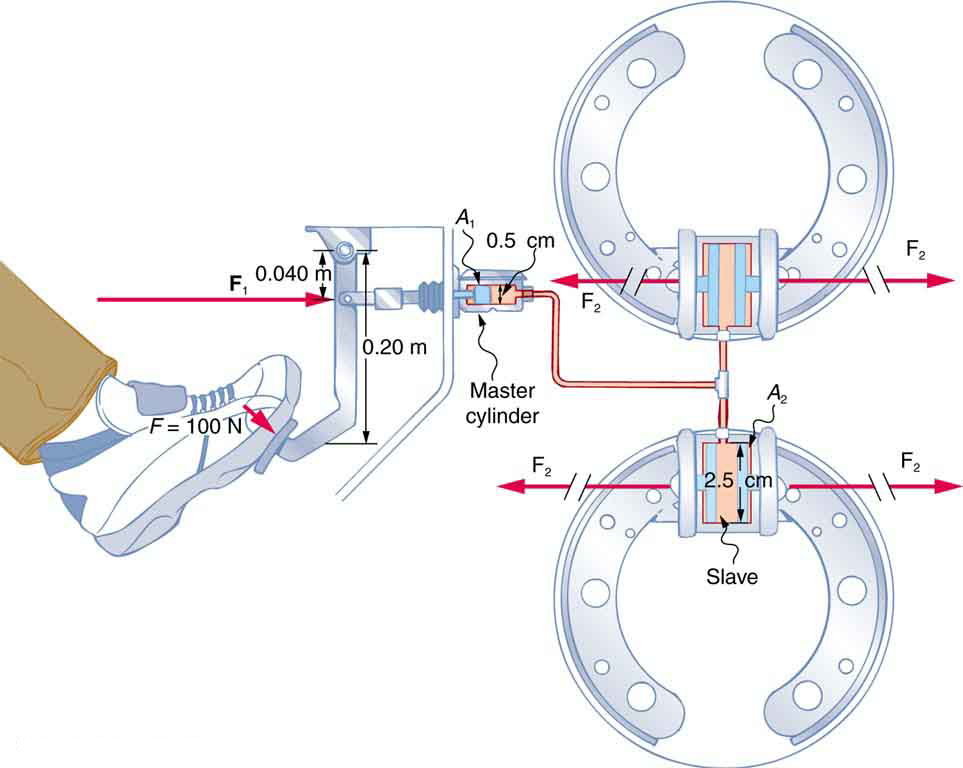
A force of 100 N is applied to the brake pedal, which acts on the cylinder—called the master—through a lever. A force of 500 N is exerted on the master cylinder. (The reader can verify that the force is 500 N using techniques of statics from Applications of Statics, Including Problem-Solving Strategies.) Pressure created in the master cylinder is transmitted to four so-called slave cylinders. The master cylinder has a diameter of 0.500 cm, and each slave cylinder has a diameter of 2.50 cm. Calculate the force [latex]{F}_{2}[/latex] created at each of the slave cylinders.

Strategy

We are given the force [latex]{F}_{1}[/latex] that is applied to the master cylinder. The cross-sectional areas [latex]{A}_{1}[/latex] and [latex]{A}_{2}[/latex] can be calculated from their given diameters. Then [latex]\frac{{F}_{1}}{{A}_{1}}=\frac{{F}_{2}}{{A}_{2}}[/latex] can be used to find the force [latex]{F}_{2}[/latex]. Manipulate this algebraically to get [latex]{F}_{2}[/latex] on one side and substitute known values:

Solution

Pascal’s principle applied to hydraulic systems is given by [latex]\frac{{F}_{1}}{{A}_{1}}=\frac{{F}_{2}}{{A}_{2}}[/latex]:

[latex]{F}_{2}=\frac{{A}_{2}}{{A}_{1}}{F}_{1}=\frac{{\mathrm{\pi r}}_{2}^{2}}{{\mathrm{\pi r}}_{1}^{2}}{F}_{1}=\frac{{\left(1.25 cm\right)}^{2}}{{\left(0.250 cm\right)}^{2}}×\text{500 N}=1\text{.}\text{25}×{\text{10}}^{4}\phantom{\rule{0.25em}{0ex}}\text{N}.[/latex]

Discussion

This value is the force exerted by each of the four slave cylinders. Note that we can add as many slave cylinders as we wish. If each has a 2.50-cm diameter, each will exert [latex]1\text{.}\text{25}×{\text{10}}^{4}\phantom{\rule{0.25em}{0ex}}\text{N}\text{.}[/latex]

A simple hydraulic system—much like a simple machine—can increase the applied force, but it cannot perform more work than the work put into it. Recall that work is the product of force and the distance over which the force acts: [latex]W = Fd[/latex]. In hydraulic systems, a force applied to the smaller, master piston causes a larger force to act on the slave piston. However, the slave piston moves a shorter distance. The more slave pistons added, the smaller the distance each one travels.

This concept underlies many real-world technologies, including power brakes and construction machinery such as bulldozers, which often incorporate motorized pumps to do most of the work. Interestingly, some organisms also rely on hydraulic principles. For instance, spiders use hydraulic pressure to extend their legs. The jumping spider, in particular, can leap up to 25 times its body length using hydraulically generated forces!

Making Connections: Conservation of Energy

The conservation of energy principle tells us that no system, including a hydraulic one, can output more energy than it receives. Since energy is transferred via work, this means that the work output from a hydraulic system can never exceed the work input:

[latex]W_{\text{out}} \leq W_{\text{in}}[/latex]

In practical systems like power brakes, motorized pumps supply the additional energy needed. Without external energy input, hydraulic systems simply redistribute force and distance according to the constraints of pressure and volume conservation.

Section Summary

• Pressure is defined as force per unit area:
  [latex]P = \frac{F}{A}[/latex]
• A change in pressure applied to an enclosed fluid is transmitted undiminished to all parts of the fluid and its container walls (Pascal’s Principle).
• Hydraulic systems use enclosed fluids to apply and transmit forces, often multiplying force while trading off distance moved.

Conceptual Questions

24. Suppose the master cylinder in a hydraulic system is at a greater height than the slave cylinder. Explain how this will affect the force produced at the slave cylinder.

Problems & Exercises

24. How much pressure is transmitted in the hydraulic system considered in Example 79.1? Express your answer in pascals and in atmospheres.
25. What force must be exerted on the master cylinder of a hydraulic lift to support the weight of a 2000-kg car (a large car) resting on the slave cylinder? The master cylinder has a 2.00-cm diameter and the slave has a 24.0-cm diameter.
26. A crass host pours the remnants of several bottles of wine into a jug after a party. He then inserts a cork with a 2.00-cm diameter into the bottle, placing it in direct contact with the wine. He is amazed when he pounds the cork into place and the bottom of the jug (with a 14.0-cm diameter) breaks away. Calculate the extra force exerted against the bottom if he pounded the cork with a 120-N force.
27. A certain hydraulic system is designed to exert a force 100 times as large as the one put into it. (a) What must be the ratio of the area of the slave cylinder to the area of the master cylinder? (b) What must be the ratio of their diameters? (c) By what factor is the distance through which the output force moves reduced relative to the distance through which the input force moves? Assume no losses to friction.
28. (a) Verify that work input equals work output for a hydraulic system assuming no losses to friction. Do this by showing that the distance the output force moves is reduced by the same factor that the output force is increased. Assume the volume of the fluid is constant. (b) What effect would friction within the fluid and between components in the system have on the output force? How would this depend on whether or not the fluid is moving?

Glossary

Pascal’s Principle

a change in pressure applied to an enclosed fluid is transmitted undiminished to all portions of the fluid and to the walls of its container