"

Dynamics: Force and Newton’s Laws of Motion and Applications: Friction, Drag and Elasticity

26 Newton’s Third Law of Motion: Symmetry in Forces

Learning Objectives

  • Understand Newton’s third law of motion.

  • Apply Newton’s third law to define systems and solve motion-related problems in biological contexts.

Forces Always Come in Pairs

In every interaction between two objects, forces always come in pairs. This principle is captured by Newton’s third law of motion:

Newton’s Third Law of Motion


Whenever one body exerts a force on a second body, the second body exerts a force equal in magnitude and opposite in direction on the first.

Mathematically, this is written as:

[latex]\mathbf{F}{\text{A on B}} = -\mathbf{F}{\text{B on A}}[/latex]

This law reveals a deep symmetry in nature: forces never occur alone. If a hand pushes on a syringe plunger, the plunger pushes back on the hand with an equal and opposite force. If a fish pushes against water to swim, the water pushes back on the fish, propelling it forward.

Applying the Law: Systems and Interactions

When analyzing motion, it’s essential to define the system of interest. Newton’s third law helps us sort which forces are internal (within the system) and which are external (acting from outside). Only external forces can change the motion of a system.

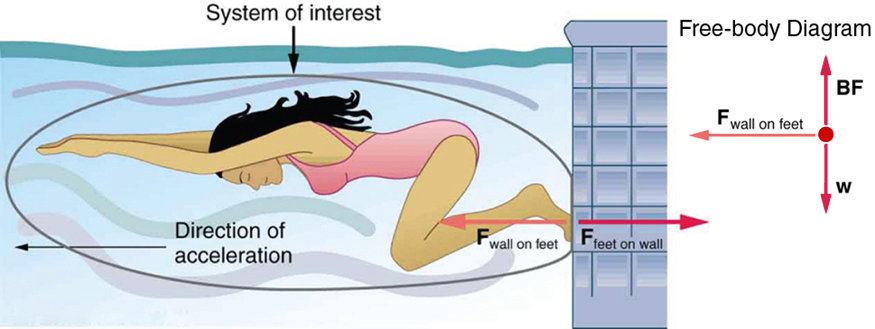
Example: Swimming and Reaction Forces

Imagine a swimmer pushing off a pool wall as illustrated in Figure 26.1. As she pushes back on the wall with her feet, the wall pushes her forward:

  • [latex]\mathbf{F}_{\text{feet on wall}}[/latex]: The action force (exerted by the swimmer on the wall).

  • [latex]\mathbf{F}_{\text{wall on feet}}[/latex]: The reaction force (exerted by the wall on the swimmer).

These forces are equal in magnitude and opposite in direction. They do not cancel because they act on different systems. Only [latex]\mathbf{F}_{\text{wall on feet}}[/latex] affects the swimmer’s motion.

A swimmer is exerting a force with her feet on a wall inside a swimming pool represented by an arrow labeled as vector F sub Feet on wall, pointing toward the right, and the wall is also exerting an equal force on her feet, represented by an arrow labeled as vector F sub Wall on feet, having the same length but pointing toward the left. The direction of acceleration of the swimmer is toward the left, shown by an arrow toward the left.
Figure 26.1: A swimmer pushes against the pool wall, and the wall pushes her in the opposite direction. The system of interest is the swimmer. The external force [latex]\mathbf{F}_{\text{wall on feet}}[/latex] causes her acceleration.

Everyday and Biological Examples of Newton’s Third Law

  • Walking and running: You push backward on the ground with your foot. The ground pushes forward on you, propelling you ahead.

  • Bird flight: Birds flap wings downward and backward, and the air pushes them upward and forward.

  • Cardiovascular applications: The heart pushes blood through arteries. The blood pushes back on the heart with equal force.

  • Muscle and bone interaction: When a muscle contracts and pulls on a bone, the bone pulls back on the muscle with equal force. This interaction is crucial in maintaining joint stability.

  • Octopus propulsion: An octopus expels water backward and moves forward due to the reaction force — a principle also used in jet propulsion.

Common Misconception: Why Forces Don’t Cancel

People often ask: “If every action has an equal and opposite reaction, why doesn’t everything stay still?” The answer lies in understanding which system is being considered. The equal and opposite forces act on different objects. For example:

  • In a rocket, the force of the gas pushing backward is on the gas, while the reaction (thrust) is on the rocket.

  • In CPR chest compressions, the rescuer exerts a downward force on the patient’s sternum, and the sternum exerts an equal upward force on the rescuer’s hands.

Only the force on the object within your defined system affects its acceleration.

Biological Context Spotlight: Breathing Mechanics

When you inhale, your diaphragm contracts downward, expanding your lungs. The lungs respond with an equal and opposite internal force as they resist this expansion. This is Newton’s third law in action: the diaphragm pulls down on the lungs, and the lungs pull up on the diaphragm. These opposing forces are vital in generating the pressure changes that drive air in and out of the body.

Example 26.1: Getting Up To Speed: Choosing the Correct System

A physics professor pushes a cart of demonstration equipment to a lecture hall, as seen in Figure 26.2. Her mass is 65.0 kg, the cart’s is 12.0 kg, and the equipment’s is 7.0 kg. Calculate the acceleration produced when the professor exerts a backward force of 150 N on the floor. All forces opposing the motion, such as friction on the cart’s wheels and air resistance, total 24.0 N.

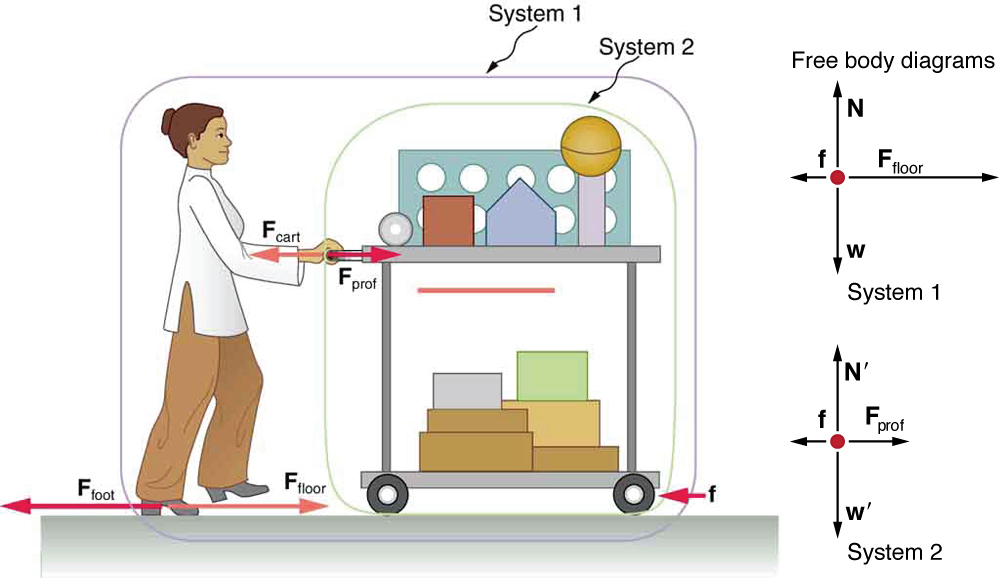
A professor is pushing a cart of demonstration equipment. Two systems are labeled in the figure. System one includes both the professor and cart, and system two only has the cart. She is exerting some force F sub prof toward the right, shown by a vector arrow, and the cart is also pushing her with the same magnitude of force directed toward the left, shown by a vector F sub cart, having same length as F sub prof. The friction force small f is shown by a vector arrow pointing left acting between the wheels of the cart and the floor. The professor is pushing the floor with her feet with a force F sub foot toward the left, shown by a vector arrow. The floor is pushing her feet with a force that has the same magnitude, F sub floor, shown by a vector arrow pointing right that has the same length as the vector F sub foot. A free-body diagram is also shown. For system one, friction force acting toward the left is shown by a vector arrow having a small length, and the force F sub floor is acting toward the right, shown by a vector arrow larger than the length of vector f. In system two, friction force represented by a short vector small f acts toward the left and another vector F sub prof is represented by a vector arrow toward the right. F sub prof is longer than small f.
Figure 26.2: A professor pushes a cart of demonstration equipment. The lengths of the arrows are proportional to the magnitudes of the forces (except for [latex]\mathbf{\text{f}}[/latex], since it is too small to draw to scale). Different questions are asked in each example; thus, the system of interest must be defined differently for each. System 1 is appropriate for Example 26.2, since it asks for the acceleration of the entire group of objects. Only [latex]{\mathbf{\text{F}}}_{\text{floor}}[/latex] and [latex]\mathbf{\text{f}}[/latex] are external forces acting on System 1 along the line of motion. All other forces either cancel or act on the outside world. System 2 is chosen for this example so that [latex]{\mathbf{\text{F}}}_{\text{prof}}[/latex] will be an external force and enter into Newton’s second law. Note that the free-body diagrams, which allow us to apply Newton’s second law, vary with the system chosen.

Strategy

Since they accelerate as a unit, we define the system to be the professor, cart, and equipment. This is System 1 in Figure 26.2. The professor pushes backward with a force [latex]{\mathbf{\text{F}}}_{\text{foot}}[/latex] of 150 N. According to Newton’s third law, the floor exerts a forward reaction force [latex]{\mathbf{\text{F}}}_{\text{floor}}[/latex] of 150 N on System 1. Because all motion is horizontal, we can assume there is no net force in the vertical direction. The problem is therefore one-dimensional along the horizontal direction. As noted, [latex]\mathbf{\text{f}}[/latex] opposes the motion and is thus in the opposite direction of [latex]{\mathbf{\text{F}}}_{\text{floor}}[/latex]. Note that we do not include the forces [latex]{\mathbf{\text{F}}}_{\text{prof}}[/latex] or [latex]{\mathbf{\text{F}}}_{\text{cart}}[/latex] because these are internal forces, and we do not include [latex]{\mathbf{\text{F}}}_{\text{foot}}[/latex] because it acts on the floor, not on the system. There are no other significant forces acting on System 1. If the net external force can be found from all this information, we can use Newton’s second law to find the acceleration as requested. See the free-body diagram in the figure.

Solution

Newton’s second law is given by

[latex]a=\frac{{F}_{\text{net}}}{m}.[/latex]

The net external force on System 1 is deduced from Figure 26.2 and the discussion above to be

[latex]{F}_{\text{net}}={F}_{\text{floor}}-f=\text{150 N}-\text{24}\text{.}\text{0 N}=\text{126 N}.[/latex]

The mass of System 1 is

[latex]m=\left(\text{65}\text{.}\text{0}+\text{12}\text{.}\text{0}+\text{7}\text{.}0\right)\phantom{\rule{0.25em}{0ex}}\text{kg}=\text{84 kg}.[/latex]

These values of [latex]{F}_{\text{net}}[/latex] and [latex]m[/latex] produce an acceleration of

[latex]\begin{array}{}a=\frac{{F}_{\text{net}}}{m},\\ a=\frac{1\text{26 N}}{\text{84 kg}}=\text{1}\text{.}{\text{5 m/s}}^{2}\text{.}\end{array}[/latex]

Discussion

None of the forces between components of System 1, such as between the professor’s hands and the cart, contribute to the net external force because they are internal to System 1. Another way to look at this is to note that forces between components of a system cancel because they are equal in magnitude and opposite in direction. For example, the force exerted by the professor on the cart results in an equal and opposite force back on her. In this case both forces act on the same system and, therefore, cancel. Thus internal forces (between components of a system) cancel. Choosing System 1 was crucial to solving this problem.

Example 26.2: Force on the Cart—Choosing a New System

Calculate the force the professor exerts on the cart in Figure 26.2 using data from the previous example if needed.

Strategy

If we now define the system of interest to be the cart plus equipment (System 2 in (Figure 26.2), then the net external force on System 2 is the force the professor exerts on the cart minus friction. The force she exerts on the cart, [latex]{\mathbf{\text{F}}}_{\text{prof}}[/latex], is an external force acting on System 2. [latex]{\mathbf{\text{F}}}_{\text{prof}}[/latex] was internal to System 1, but it is external to System 2 and will enter Newton’s second law for System 2.

Solution

Newton’s second law can be used to find [latex]{\mathbf{\text{F}}}_{\text{prof}}[/latex]. Starting with

[latex]a=\frac{{F}_{\text{net}}}{m}[/latex]

and noting that the magnitude of the net external force on System 2 is

[latex]{F}_{\text{net}}={F}_{\text{prof}}-f,[/latex]

we solve for [latex]{F}_{\text{prof}}[/latex], the desired quantity:

[latex]{F}_{\text{prof}}={F}_{\text{net}}+f.[/latex]

The value of [latex]f[/latex] is given, so we must calculate net [latex]{F}_{\text{net}}[/latex]. That can be done since both the acceleration and mass of System 2 are known. Using Newton’s second law we see that

[latex]{F}_{\text{net}}=\text{ma},[/latex]

where the mass of System 2 is 19.0 kg ([latex]m[/latex]= 12.0 kg + 7.0 kg) and its acceleration was found to be [latex]a=1.5\phantom{\rule{0.25em}{0ex}}{\text{m/s}}^{2}[/latex] in the previous example. Thus,

[latex]{F}_{\text{net}}=\text{ma},[/latex]
[latex]{F}_{\text{net}}=\left(\text{19}\text{.}\text{0 kg}\right)\left(1.5\phantom{\rule{0.25em}{0ex}}{\text{m/s}}^{2}\right)=\text{29 N}.[/latex]

Now we can find the desired force:

[latex]{F}_{\text{prof}}={F}_{\text{net}}+f,[/latex]
[latex]{F}_{\text{prof}}=\text{29 N}+\text{24.0 N}=\text{53 N}.[/latex]

Discussion

It is interesting that this force is significantly less than the 150-N force the professor exerted backward on the floor. Not all of that 150-N force is transmitted to the cart; some of it accelerates the professor.

The choice of a system is an important analytical step both in solving problems and in thoroughly understanding the physics of the situation (which is not necessarily the same thing).

PhET Explorations: Gravity Force Lab

Visualize the gravitational force that two objects exert on each other. Change properties of the objects in order to see how it changes the gravity force.

Section Summary

  • Newton’s third law of motion represents a basic symmetry in nature. It states: Whenever one body exerts a force on a second body, the first body experiences a force that is equal in magnitude and opposite in direction to the force that the first body exerts.
  • A thrust is a reaction force that pushes a body forward in response to a backward force. Rockets, airplanes, and cars are pushed forward by a thrust reaction force.

Conceptual Questions

  1. When you take off in a jet aircraft, there is a sensation of being pushed back into the seat. Explain why you move backward in the seat—is there really a force backward on you? (The same reasoning explains whiplash injuries, in which the head is apparently thrown backward.)
  2. A device used since the 1940s to measure the kick or recoil of the body due to heart beats is the “ballistocardiograph.” What physics principle(s) are involved here to measure the force of cardiac contraction? How might we construct such a device?
  3. Describe a situation in which one system exerts a force on another and, as a consequence, experiences a force that is equal in magnitude and opposite in direction. Which of Newton’s laws of motion apply?
  4. Why does an ordinary rifle recoil (kick backward) when fired? The barrel of a recoilless rifle is open at both ends. Describe how Newton’s third law applies when one is fired. Can you safely stand close behind one when it is fired?
  5. An American football lineman reasons that it is senseless to try to out-push the opposing player, since no matter how hard he pushes he will experience an equal and opposite force from the other player. Use Newton’s laws and draw a free-body diagram of an appropriate system to explain how he can still out-push the opposition if he is strong enough.
  6. Newton’s third law of motion tells us that forces always occur in pairs of equal and opposite magnitude. Explain how the choice of the “system of interest” affects whether one such pair of forces cancels.

Problem Exercises

  1. What net external force is exerted on a 1100-kg artillery shell fired from a battleship if the shell is accelerated at [latex]2\text{.}\text{40}×{\text{10}}^{4}\phantom{\rule{0.25em}{0ex}}{\text{m/s}}^{2}[/latex]? What is the magnitude of the force exerted on the ship by the artillery shell?
    Force on shell: [latex]2\text{.}\text{64}×{\text{10}}^{7}\phantom{\rule{0.25em}{0ex}}\text{N}[/latex]
    Force exerted on ship = [latex]-2\text{.}\text{64}×{\text{10}}^{7}\phantom{\rule{0.25em}{0ex}}\text{N}[/latex], by Newton’s third law
  2. A brave but inadequate rugby player is being pushed backward by an opposing player who is exerting a force of 800 N on him. The mass of the losing player plus equipment is 90.0 kg, and he is accelerating at [latex]1\text{.}\text{20}\phantom{\rule{0.25em}{0ex}}{\text{m/s}}^{2}[/latex] backward.
    1. What is the force of friction between the losing player’s feet and the grass?
    2. What force does the winning player exert on the ground to move forward if his mass plus equipment is 110 kg?
    3. Draw a sketch of the situation showing the system of interest used to solve each part. For this situation, draw a free-body diagram and write the net force equation.

Glossary

Newton’s third law of motion
whenever one body exerts a force on a second body, the first body experiences a force that is equal in magnitude and opposite in direction to the force that the first body exerts
thrust
a reaction force that pushes a body forward in response to a backward force; rockets, airplanes, and cars are pushed forward by a thrust reaction force
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book