Fluid Dynamics and Its Biological and Medical Applications
91 Molecular Transport Phenomena: Diffusion, Osmosis, and Related Processes
Learning Objectives
Diffusion
Why does an ice cube from your freezer sometimes smell like fish or leftovers? How does soaking an inflamed ankle in an Epsom salt solution help reduce swelling? Both of these questions involve the microscopic transport of molecules known as diffusion, a type of passive transport critical to many biological processes.
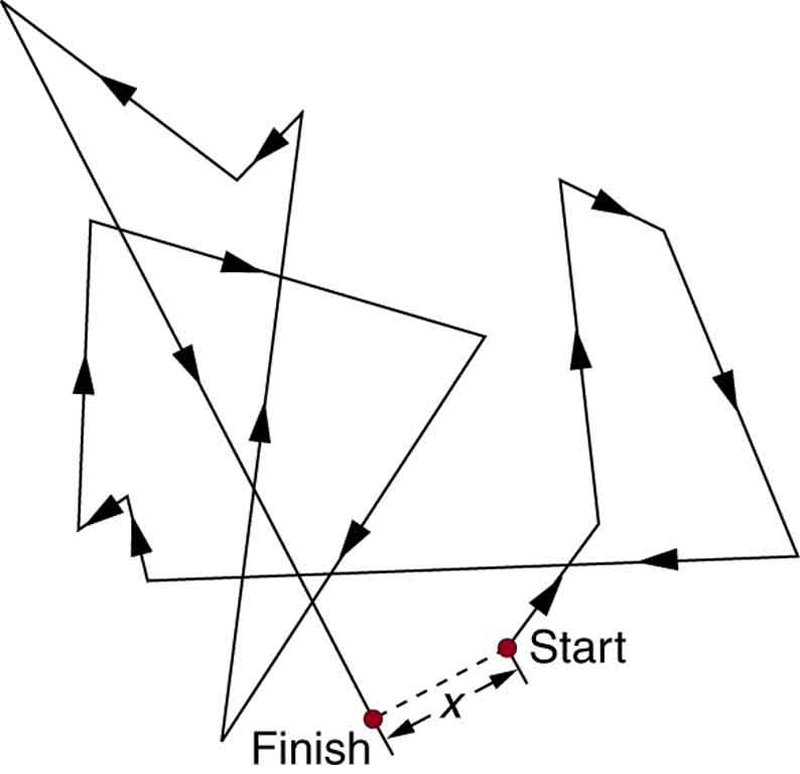
Atoms and molecules are constantly in motion due to thermal energy, even when no large-scale flow occurs. This motion is known as a random walk and results in diffusion, the spread of substances from areas of higher concentration to lower concentration due to random molecular motion. As shown in Figure 91.1, this motion is unpredictable at the individual level, but collectively, it leads to the even mixing of molecules.
Diffusion plays a vital role in biological systems—for example, in how oxygen crosses from alveoli into capillaries or how nutrients move into cells. However, it is relatively slow over large distances because molecules undergo frequent collisions that randomize their paths. The average distance a molecule diffuses in time [latex]t[/latex] is described by:
This equation gives the root-mean-square distance [latex]{x}_{\text{rms}}[/latex], the statistical average distance traveled. The constant [latex]D[/latex] is the diffusion coefficient, which varies depending on the molecule and the medium. Smaller molecules and gases generally have larger [latex]D[/latex] values than larger or more complex molecules, especially in liquids like water.
The values of [latex]D[/latex] for various molecules are shown in Table 91.1. Notice that lighter, smaller molecules such as hydrogen and oxygen diffuse more rapidly than heavier molecules such as glucose, hemoglobin, or DNA.
| Diffusing molecule | Medium | D (m2/s) |
|---|---|---|
| Hydrogen [latex]\left({\text{H}}_{2}\right)[/latex] | Air | [latex]6.4×{10}^{–5}[/latex] |
| Oxygen [latex]\left({\text{O}}_{2}\right)[/latex] | Air | [latex]1.8×{10}^{–5}[/latex] |
| Oxygen [latex]\left({\text{O}}_{2}\right)[/latex] | Water | [latex]1.0×{10}^{–9}[/latex] |
| Glucose [latex]\left({\text{C}}_{6}{\text{H}}_{12}{\text{O}}_{6}\right)[/latex] | Water | [latex]6.7×{10}^{–10}[/latex] |
| Hemoglobin | Water | [latex]6.9×{10}^{–11}[/latex] |
| DNA | Water | [latex]1.3×{10}^{–12}[/latex] |
As the data show, the diffusion constant [latex]D[/latex] decreases with increasing molecular size. This occurs because larger molecules move more slowly due to their greater mass and increased likelihood of collisions. For instance, oxygen diffuses about 64,000 times faster in air than in water because collisions occur much more frequently in the denser liquid medium. In water, an oxygen molecule travels only about [latex]40\ \mu \text{m}[/latex] in 1 second—barely enough to span the width of a human hair!
Finally, diffusion is strongly temperature-dependent. As temperature increases, molecular kinetic energy increases, which leads to faster diffusion. This is consistent with the relationship:
where [latex]m[/latex] is mass, [latex]v[/latex] is speed, and [latex]T[/latex] is absolute temperature. As a result, diffusion processes occur more rapidly in warm conditions—something that has important implications in physiology and medical treatments.
Example 91.1 Calculating Diffusion: How Long Does Glucose Diffusion Take?
Calculate the average time it takes a glucose molecule to move 1.0 cm in water.
Strategy
We can use [latex]{x}_{\text{rms}}=\sqrt{2D\text{t}}[/latex], the expression for the average distance moved in time [latex]t[/latex], and solve it for [latex]t[/latex]. All other quantities are known.
Solution
Solving for [latex]t[/latex] and substituting known values yields
Discussion
This is a remarkably long time for glucose to move a mere centimeter! For this reason, we stir sugar into water rather than waiting for it to diffuse.
Diffusion at Small Scales
Because diffusion is typically very slow over long distances, its most significant effects occur on small scales. For example, the cornea of the eye—devoid of blood vessels—receives most of its oxygen via diffusion through the thin tear layer that covers its surface.
The Rate and Direction of Diffusion
If you gently place a drop of food coloring into still water, you will observe it slowly spread out until the color becomes uniform. This process is known as free diffusion—a form of diffusion unhindered by physical barriers. At the molecular level, particles move randomly in all directions due to thermal energy. However, because more molecules start in regions of higher concentration, there is a net movement from high to low concentration. Over time, this net flow diminishes as concentrations become more equal. (See Figure 91.2.)
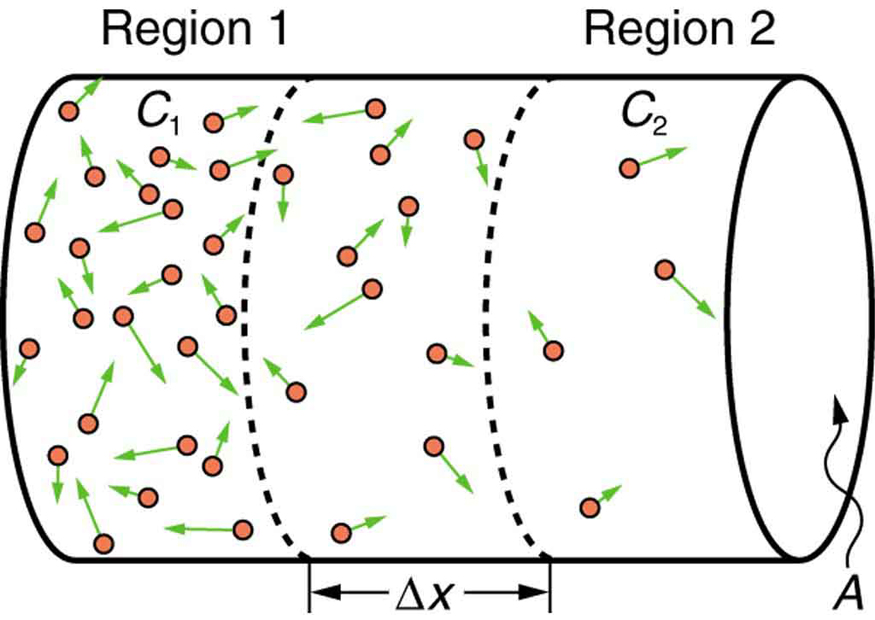
The rate of diffusion is directly proportional to the difference in concentration and the diffusion constant [latex]D[/latex]. More molecules leave a region of high concentration than enter it from a region of lower concentration. If concentrations are equal, the net movement is zero, even though individual molecules continue to move randomly.
Many biological processes rely heavily on diffusion. For instance, diffusion enables the exchange of oxygen, carbon dioxide, nutrients, and waste between blood and tissues, and between alveoli and capillaries in the lungs. However, as organisms evolved and increased in size, diffusion alone became insufficient for internal transport—leading to the development of circulatory systems. In contrast, single-celled organisms still depend entirely on diffusion.
Osmosis and Dialysis—Diffusion across Membranes
Some of the most biologically relevant diffusion processes occur across membranes, which can influence the rate and selectivity of transport. For example, soaking a swollen ankle in an Epsom salt solution draws water out of the tissues via diffusion through the skin. In cells, numerous substances—including oxygen, carbon dioxide, glucose, and waste products—routinely diffuse through the cell membrane.
Membranes are typically semipermeable, allowing certain substances to pass while restricting others. This can occur through small pores that let only small molecules through or via chemical interactions that enable diffusion. (See Figure 91.3.)
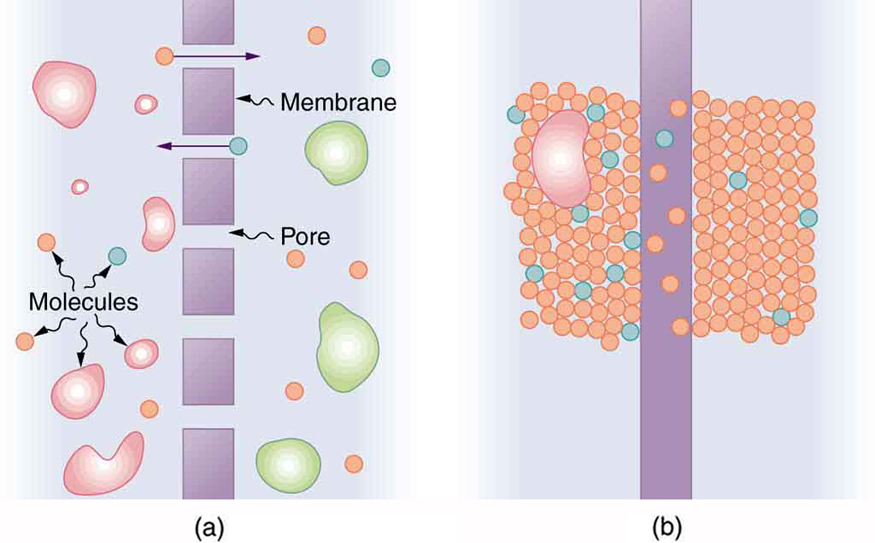
Osmosis is the diffusion of water through a semipermeable membrane from a region of higher water concentration to lower water concentration. For example, when soaking in Epsom salt, water exits the body into the salt solution because the water concentration is higher in your tissues than in the surrounding fluid. Similarly, dialysis refers to the diffusion of solutes (other than water) across a semipermeable membrane due to a concentration difference.
Osmosis can create substantial pressure. If allowed to proceed without restraint, the accumulation of water on one side of a membrane generates a hydrostatic pressure that eventually halts further net flow. This back pressure is quantified by:
where [latex]\rho[/latex] is the fluid density, [latex]g[/latex] is the acceleration due to gravity, and [latex]h[/latex] is the height difference created by osmosis. If one of the solutions is pure water, this pressure is called the osmotic pressure. (See Figure 91.4.)
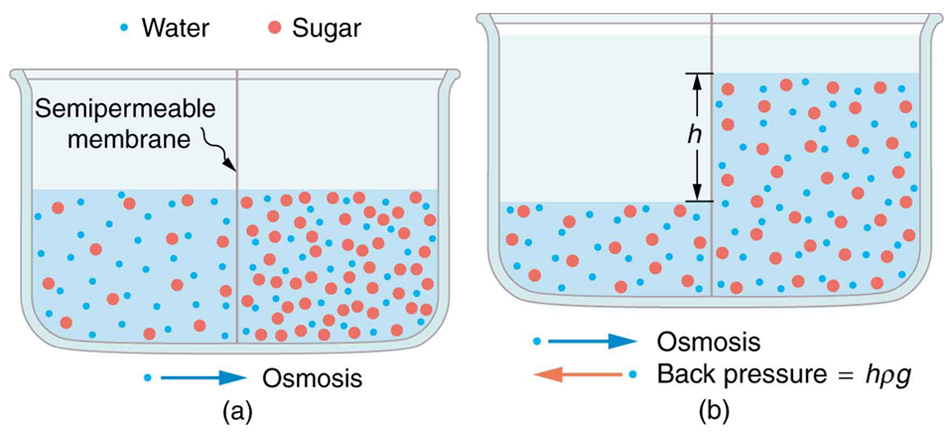
Osmotic pressures can be very large. For example, separating seawater and pure water with a membrane that blocks salt can generate an osmotic pressure of nearly 26 atmospheres. In plants, osmotic pressure contributes to turgor—the outward pressure of cell fluid against the wall, providing structural support.
Processes like reverse osmosis and reverse dialysis (or filtration) occur when a large enough back pressure forces water or solutes to move against their concentration gradients. These methods are used to purify water or filter substances in clinical and industrial settings.
Occasionally, substances move across membranes in the “wrong” direction—not due to pressure but due to energy-driven processes called active transport. For example, cypress tree roots absorb fresh water from salt water—a feat that requires cellular energy rather than relying on passive osmosis. Active transport is essential in kidney function, nerve signaling, and nutrient uptake, and it accounts for a significant portion of our body’s energy use—about 25% at the cellular level.
Section Summary
- Diffusion is the passive movement of particles due to thermal motion, leading to net movement from regions of high to low concentration.
- The average distance a molecule diffuses over time is given by:
[latex]{x}_{\text{rms}} = \sqrt{2Dt}[/latex]
where [latex]D[/latex] is the diffusion constant, values of which are listed in Table 91.1.
- Osmosis is the diffusion of water across a semipermeable membrane from high to low water concentration.
- Dialysis is the diffusion of solutes across a semipermeable membrane due to concentration gradients.
- Both processes can be reversed using sufficient back pressure.
- Active transport uses energy to move substances against their natural gradients and is essential for many cellular functions.
Conceptual Questions
- Why would you expect the rate of diffusion to increase with temperature? Can you give an example, such as the fact that you can dissolve sugar more rapidly in hot water?
- How are osmosis and dialysis similar? How do they differ?
Problem Exercises
- You can smell perfume very shortly after opening the bottle. To show that it is not reaching your nose by diffusion, calculate the average distance a perfume molecule moves in one second in air, given its diffusion constant [latex]D[/latex] to be [latex]1.00×{\text{10}}^{–6}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{2}\text{/s}[/latex].
- What is the ratio of the average distances that oxygen will diffuse in a given time in air and water? Why is this distance less in water (equivalently, why is [latex]D[/latex] less in water)?
- Oxygen reaches the veinless cornea of the eye by diffusing through its tear layer, which is 0.500-mm thick. How long does it take the average oxygen molecule to do this?
- (a) Find the average time required for an oxygen molecule to diffuse through a 0.200-mm-thick tear layer on the cornea. (b) How much time is required to diffuse [latex]0\text{.500}\phantom{\rule{0.25em}{0ex}}{\text{cm}}^{3}[/latex] of oxygen to the cornea if its surface area is [latex]1\text{.}\text{00}\phantom{\rule{0.25em}{0ex}}{\text{cm}}^{2}[/latex]?
- Suppose hydrogen and oxygen are diffusing through air. A small amount of each is released simultaneously. How much time passes before the hydrogen is 1.00 s ahead of the oxygen? Such differences in arrival times are used as an analytical tool in gas chromatography.
Footnotes
- At 20°C and 1 atm.↵
Glossary
- diffusion
- the movement of substances due to random thermal molecular motion
- semipermeable
- a type of membrane that allows only certain small molecules to pass through
- osmosis
- the transport of water through a semipermeable membrane from a region of high concentration to one of low concentration
- dialysis
- the transport of any molecule other than water through a semipermeable membrane from a region of high concentration to one of low concentration
- relative osmotic pressure
- the back pressure which stops the osmotic process if neither solution is pure water
- osmotic pressure
- the back pressure which stops the osmotic process if one solution is pure water
- reverse osmosis
- the process that occurs when back pressure is sufficient to reverse the normal direction of osmosis through membranes
- active transport
- the process in which a living membrane expends energy to move substances across
the movement of substances due to random thermal molecular motion
the transport of water through a semipermeable membrane from a region of high concentration to one of low concentration
the transport of any molecule other than water through a semipermeable membrane from a region of high concentration to one of low concentration
the process that occurs when back pressure is sufficient to reverse the normal direction of osmosis through membranes
the process in which a living membrane expends energy to move substances across
a type of membrane that allows only certain small molecules to pass through
the back pressure which stops the osmotic process if neither solution is pure water
the back pressure which stops the osmotic process if one solution is pure water

