"

Rotational motion and angular momentum

72 Kinematics of Rotational Motion

Learning Objectives

  • Describe the basic concepts of rotational motion, including angular displacement, velocity, and acceleration.
  • Apply rotational kinematic equations to solve problems involving angular motion with constant acceleration.
  • Compare and contrast rotational kinematics with translational kinematics.

The study of helps us understand how objects spin, turn, or rotate. Just as we use position, velocity, and acceleration to describe straight-line motion, we can define angular displacement [latex]\theta[/latex], angular velocity [latex]\omega[/latex], and angular acceleration [latex]\alpha[/latex] to describe rotational motion.

Imagine a motorcycle tire accelerating as the rider opens the throttle. The wheel spins faster and faster, rotating through many revolutions. If the angular acceleration [latex]\alpha[/latex] is large and sustained over time [latex]t[/latex], the tire’s angular velocity [latex]\omega[/latex] and angle of rotation [latex]\theta[/latex] increase significantly. This relationship mirrors linear motion, where a constant acceleration leads to increasing velocity and greater displacement.

focuses on describing motion without considering the forces that cause it. For rotational motion, we can derive equations that link [latex]\theta[/latex], [latex]\omega[/latex], [latex]\alpha[/latex], and time [latex]t[/latex]—in much the same way we did for translational motion.

We begin with the linear kinematic equation:

[latex]v = v_0 + at \quad \text{(constant } a)[/latex]

For circular motion, the tangential velocity is related to angular velocity via [latex]v = r\omega[/latex], and tangential acceleration is [latex]a = r\alpha[/latex]. Substituting these into the equation and dividing both sides by [latex]r[/latex] gives:

[latex]\omega = \omega_0 + \alpha t \quad \text{(constant } \alpha)[/latex]

This is the first rotational kinematic equation, and it is directly analogous to its linear counterpart.

Making Connections

Just as displacement, velocity, and acceleration describe linear motion, angular displacement, angular velocity, and angular acceleration describe rotational motion. These quantities are connected through kinematic equations, as first explored in One-Dimensional Kinematics.

From our earlier work, we can write the full set of kinematic equations for rotational motion, assuming constant angular acceleration. These are summarized in comparison to the translational versions in the following table:

Table 72.1 Rotational Kinematic Equations
Rotational Translational
[latex]\theta =\overline{\omega }t[/latex] [latex]x=\stackrel{-}{v}t[/latex]
[latex]\omega ={\omega }_{0}+\mathrm{\alpha t}[/latex] [latex]v={v}_{0}+\text{at}[/latex] (constant [latex]\alpha[/latex], [latex]a[/latex])
[latex]\theta ={\omega }_{0}t+\frac{1}{2}{\mathrm{\alpha t}}^{2}[/latex] [latex]x={v}_{0}t+\frac{1}{2}{\text{at}}^{2}[/latex] (constant [latex]\alpha[/latex], [latex]a[/latex])
[latex]{\omega }^{2}={{\omega }_{0}}^{2}+2\text{αθ}[/latex] [latex]{v}^{2}={{v}_{0}}^{2}+2\text{ax}[/latex] (constant [latex]\alpha[/latex], [latex]a[/latex])

In these equations in Table 72.1:

  • [latex]\omega_0[/latex] and [latex]v_0[/latex] are the initial angular and linear velocities
  • [latex]\theta[/latex] and [latex]x[/latex] are angular and linear displacements
  • [latex]\bar{\omega} = \frac{\omega_0 + \omega}{2}[/latex] is average angular velocity
  • [latex]\bar{v} = \frac{v_0 + v}{2}[/latex] is average linear velocity

Problem-Solving Strategy for Rotational Kinematics

  1. Confirm the motion is rotational, and constant angular acceleration applies.
  2. Identify what is being asked for. Is it [latex]\theta[/latex], [latex]\omega[/latex], or [latex]\alpha[/latex]?
  3. List known quantities. Include any given values or initial conditions.
  4. Select the appropriate equation. Use one of the four kinematic relationships.
  5. Solve algebraically first, then substitute in numbers and units.
  6. Check the result. Does the value and unit make physical sense?

Example 72.1 Calculating the Acceleration of a Fishing Reel

A deep-sea fisherman hooks a big fish that swims away from the boat pulling the fishing line from his fishing reel. The whole system is initially at rest and the fishing line unwinds from the reel at a radius of 4.50 cm from its axis of rotation. The reel is given an angular acceleration of [latex]\text{110}\phantom{\rule{0.25em}{0ex}}{\text{rad/s}}^{2}[/latex] for 2.00 s as seen in Figure 72.1.

  1. What is the final angular velocity of the reel?
  2. At what speed is fishing line leaving the reel after 2.00 s elapses?
  3. How many revolutions does the reel make?
  4. How many meters of fishing line come off the reel in this time?
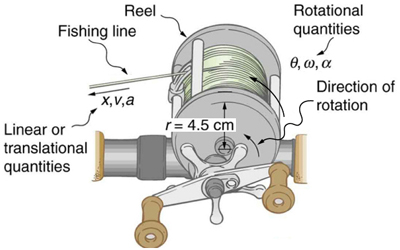
The figure shows a fishing reel, with radius equal to 4.5 centimeters. The direction of rotation of the reel is counterclockwise. The rotational quantities are theta, omega and alpha, and x, v, a are linear or translational quantities. The reel, fishing line, and the direction of motion have been separately indicated by curved arrows pointing toward those parts.
Figure 72.1 Fishing line coming off a rotating reel moves linearly. Example 72.1 and Example 72.2 consider relationships between rotational and linear quantities associated with a fishing reel.

Strategy

In each part of this example, the strategy is the same as it was for solving problems in linear kinematics. In particular, known values are identified and a relationship is then sought that can be used to solve for the unknown.

Solution for (a)

Here [latex]\alpha[/latex] and [latex]t[/latex] are given and [latex]\omega[/latex] needs to be determined. The most straightforward equation to use is [latex]\omega ={\omega }_{0}+\mathrm{\alpha t}[/latex] because the unknown is already on one side and all other terms are known. That equation states that [latex]\omega ={\omega }_{0}+\mathrm{\alpha t}\text{.}[/latex]

We are also given that [latex]{\omega }_{0}=0[/latex] (it starts from rest), so that [latex]\omega =0+\left(\text{110}\phantom{\rule{0.25em}{0ex}}{\text{rad/s}}^{2}\right)\left(2\text{.}\text{00}\text{s}\right)=\text{220}\phantom{\rule{0.25em}{0ex}}\text{rad/s}\text{.}[/latex]

Solution for (b)

Now that [latex]\omega[/latex] is known, the speed [latex]v[/latex] can most easily be found using the relationship

[latex]v=\mathrm{r\omega }\text{,}[/latex]

where the radius [latex]r[/latex] of the reel is given to be 4.50 cm; thus,

[latex]v=\left(0\text{.}\text{0450 m}\right)\left(\text{220 rad/s}\right)=9\text{.}\text{90 m/s.}[/latex]

Note again that radians must always be used in any calculation relating linear and angular quantities. Also, because radians are dimensionless, we have [latex]\text{m}×\text{rad}=\text{m}[/latex].

Solution for (c)

Here, we are asked to find the number of revolutions. Because [latex]\text{1 rev}=\text{2π rad}[/latex], we can find the number of revolutions by finding [latex]\theta[/latex] in radians. We are given [latex]\alpha[/latex] and [latex]t[/latex], and we know [latex]{\omega }_{{}_{0}}[/latex] is zero, so that [latex]\theta[/latex] can be obtained using [latex]\theta ={\omega }_{0}t+\frac{1}{2}{\mathrm{\alpha t}}^{2}[/latex].

[latex]\begin{array}{lll}\theta & =& {\omega }_{0}t+\frac{1}{2}{\mathrm{\alpha t}}^{2}\\ & =& 0+\left(\text{0.500}\right)\left(\text{110}\phantom{\rule{0.25em}{0ex}}{\text{rad/s}}^{2}\right){\left(\text{2.00 s}\right)}^{2}=\text{220 rad}.\end{array}[/latex]

Converting radians to revolutions gives

[latex]\theta =\left(\text{220 rad}\right)\frac{\text{1 rev}}{\text{2π rad}}=\text{35.0 rev.}[/latex]

Solution for (d)

The number of meters of fishing line is [latex]x[/latex], which can be obtained through its relationship with [latex]\theta[/latex]:

[latex]x=\mathrm{r\theta }=\left(\text{0.0450 m}\right)\left(\text{220 rad}\right)=\text{9.90 m}.[/latex]

Discussion

This example illustrates that relationships among rotational quantities are highly analogous to those among linear quantities. We also see in this example how linear and rotational quantities are connected. The answers to the questions are realistic. After unwinding for two seconds, the reel is found to spin at 220 rad/s, which is 2100 rpm. (No wonder reels sometimes make high-pitched sounds.) The amount of fishing line played out is 9.90 m, about right for when the big fish bites.

Example 72.2 Calculating the Duration When the Fishing Reel Slows Down and Stops

Now let us consider what happens if the fisherman applies a brake to the spinning reel, achieving an angular acceleration of [latex]–\text{300}\phantom{\rule{0.25em}{0ex}}{\text{rad/s}}^{2}[/latex]. How long does it take the reel to come to a stop?

Strategy

We are asked to find the time [latex]t[/latex] for the reel to come to a stop. The initial and final conditions are different from those in the previous problem, which involved the same fishing reel. Now we see that the initial angular velocity is [latex]{\omega }_{0}=\text{220 rad/s}[/latex] and the final angular velocity [latex]\omega[/latex] is zero. The angular acceleration is given to be [latex]\alpha =-\text{300}\phantom{\rule{0.25em}{0ex}}{\text{rad/s}}^{2}[/latex]. Examining the available equations, we see all quantities but t are known in [latex]\omega ={\omega }_{0}+\mathrm{\alpha t},[/latex] making it easiest to use this equation.

Solution

The equation states

[latex]\omega ={\omega }_{0}+\mathrm{\alpha t}\text{.}[/latex]

We solve the equation algebraically for t, and then substitute the known values as usual, yielding

[latex]t=\frac{\omega -{\omega }_{0}}{\alpha }=\frac{0-\text{220 rad/s}}{-\text{300}\phantom{\rule{0.25em}{0ex}}{\text{rad/s}}^{2}}=0\text{.}\text{733 s.}[/latex]

Discussion

Note that care must be taken with the signs that indicate the directions of various quantities. Also, note that the time to stop the reel is fairly small because the acceleration is rather large. Fishing lines sometimes snap because of the accelerations involved, and fishermen often let the fish swim for a while before applying brakes on the reel. A tired fish will be slower, requiring a smaller acceleration.

Example 72.3: Calculating the Slow Acceleration of Trains and Their Wheels

Large freight trains accelerate very slowly. Suppose one such train accelerates from rest, giving its 0.350-m-radius wheels an angular acceleration of [latex]0\text{.}\text{250}\phantom{\rule{0.25em}{0ex}}{\text{rad/s}}^{2}[/latex]. After the wheels have made 200 revolutions (assume no slippage): (a) How far has the train moved down the track? (b) What are the final angular velocity of the wheels and the linear velocity of the train?

Strategy

In part (a), we are asked to find [latex]x[/latex], and in (b) we are asked to find [latex]\omega[/latex] and [latex]v[/latex]. We are given the number of revolutions [latex]\theta[/latex], the radius of the wheels [latex]r[/latex], and the angular acceleration [latex]\alpha[/latex].

Solution for (a)

The distance [latex]x[/latex] is very easily found from the relationship between distance and rotation angle:

[latex]\theta =\frac{x}{r}.[/latex]

Solving this equation for [latex]x[/latex] yields

[latex]x=\mathrm{r\theta .}[/latex]

Before using this equation, we must convert the number of revolutions into radians, because we are dealing with a relationship between linear and rotational quantities:

[latex]\theta =\left(\text{200}\phantom{\rule{0.25em}{0ex}}\text{rev}\right)\frac{2\pi \phantom{\rule{0.25em}{0ex}}\text{rad}}{\text{1 rev}}=\text{1257}\phantom{\rule{0.25em}{0ex}}\text{rad}.[/latex]

Now we can substitute the known values into [latex]x=\mathrm{r\theta }[/latex] to find the distance the train moved down the track:

[latex]x=\mathrm{r\theta }=\left(0.350 m\right)\left(\text{1257 rad}\right)=\text{440}\phantom{\rule{0.25em}{0ex}}\text{m}.[/latex]

Solution for (b)

We cannot use any equation that incorporates [latex]t[/latex] to find [latex]\omega[/latex], because the equation would have at least two unknown values. The equation [latex]{\omega }^{2}={{\omega }_{0}}^{2}+2\text{αθ}[/latex] will work, because we know the values for all variables except [latex]\omega[/latex]:

[latex]{\omega }^{2}={{\omega }_{0}}^{2}+2\text{αθ}[/latex]

Taking the square root of this equation and entering the known values gives

[latex]\begin{array}{lll}\omega & =& {\left[0+2\left(0\text{.}\text{250}{\text{ rad/s}}^{2}\right)\left(\text{1257}\text{ rad}\right)\right]}^{1/2}\\ & =& \text{25.1 rad/s.}\end{array}[/latex]

We can find the linear velocity of the train, [latex]v[/latex], through its relationship to [latex]\omega[/latex]:

[latex]v=\mathrm{r\omega }=\left(0.350 m\right)\left(\text{25.1 rad/s}\right)=\text{8.77 m/s}.[/latex]

Discussion

The distance traveled is fairly large and the final velocity is fairly slow (just under 32 km/h).

There is translational motion even for something spinning in place, as the following example illustrates. Figure 72.2 shows a fly on the edge of a rotating microwave oven plate. The example below calculates the total distance it travels.

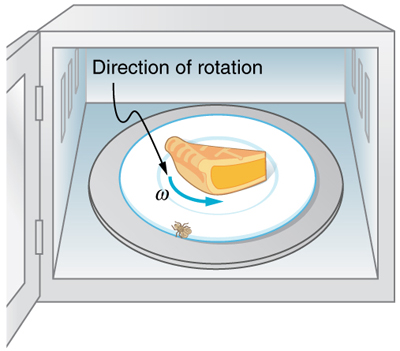
The figure shows a fly that has landed on the rotating plate of the microwave. The direction of rotation of the plate, omega, is counterclockwise and is shown with an arrow.
Figure 72.2 The image shows a microwave plate. The fly makes revolutions while the food is heated (along with the fly).

Example 72.4: Calculating the Distance Traveled by a Fly on the Edge of a Microwave Oven Plate

A person decides to use a microwave oven to reheat some lunch. In the process, a fly accidentally flies into the microwave and lands on the outer edge of the rotating plate and remains there. If the plate has a radius of 0.15 m and rotates at 6.0 rpm, calculate the total distance traveled by the fly during a 2.0-min cooking period. (Ignore the start-up and slow-down times.)

Strategy

First, find the total number of revolutions [latex]\theta[/latex], and then the linear distance [latex]x[/latex] traveled. [latex]\theta =\overline{\omega }t[/latex] can be used to find [latex]\theta[/latex] because [latex]\stackrel{-}{\omega }[/latex]
is given to be 6.0 rpm.

Solution

Entering known values into [latex]\theta =\overline{\omega }t[/latex] gives

[latex]\theta =\stackrel{-}{\omega }t=\left(\text{6.0 rpm}\right)\left(\text{2.0 min}\right)=\text{12 rev}.[/latex]

As always, it is necessary to convert revolutions to radians before calculating a linear quantity like [latex]x[/latex] from an angular quantity like [latex]\theta[/latex]:

[latex]\theta =\left(\text{12 rev}\right)\left(\frac{2\pi \phantom{\rule{0.25em}{0ex}}\text{rad}}{\text{1 rev}}\right)=\text{75}\text{.4 rad.}[/latex]

Now, using the relationship between [latex]x[/latex] and [latex]\theta[/latex], we can determine the distance traveled:

[latex]x=\mathrm{r\theta }=\left(0\text{.}\text{15}\text{ m}\right)\left(\text{75}\text{.}4\text{ rad}\right)=\text{11}\text{ m}.[/latex]

Discussion

Quite a trip (if it survives)! Note that this distance is the total distance traveled by the fly. Displacement is actually zero for complete revolutions because they bring the fly back to its original position. The distinction between total distance traveled and displacement was first noted in One-Dimensional Kinematics.

Check Your Understanding

Question: Rotational kinematics provides many useful mathematical relationships, such as [latex]\omega = \omega_0 + \alpha t[/latex]. Are these relationships considered laws of physics, or are they simply descriptive tools? (Hint: Consider the same question for linear kinematics.)

Answer: The equations of rotational kinematics, like those of linear kinematics, are descriptive—not fundamental laws of nature. They allow us to precisely describe motion under the assumption of constant acceleration but do not explain the causes of that motion. For instance, a large angular acceleration tells us that the object’s angular velocity is changing rapidly, but it says nothing about what is producing that acceleration. That cause is addressed in dynamics, through Newton’s laws and torque.

Section Summary

  • Kinematics is the branch of physics that describes motion without considering its causes. It applies to both linear and rotational motion.
  • The kinematics of rotational motion involves the relationships among rotation angle (θ), angular velocity (ω), angular acceleration (α), and time (t).
  • The four equations of rotational kinematics are direct analogs to the four linear (translational) kinematic equations introduced in One-Dimensional Kinematics. These are summarized side-by-side in Table 72.1.
  • In these equations, the subscript 0 indicates initial values, such as [latex]{x}_{0}[/latex] and [latex]{\omega}_{0}[/latex], and average quantities are defined as follows:
    [latex]\overline{\omega} = \frac{{\omega}_{0} + \omega}{2} \quad \text{and} \quad \overline{v} = \frac{{v}_{0} + v}{2}[/latex]

Problems & Exercises

  1. With the aid of a string, a gyroscope is accelerated from rest to 32 rad/s in 0.40 s. (a) What is its angular acceleration in rad/s2? (b) How many revolutions does it go through in the process?
  2. Suppose a piece of dust finds itself on a CD. If the spin rate of the CD is 500 rpm, and the piece of dust is 4.3 cm from the center, what is the total distance traveled by the dust in 3 minutes? (Ignore accelerations due to getting the CD rotating.)
  3. A gyroscope slows from an initial rate of 32.0 rad/s at a rate of [latex]0\text{.}\text{700}{\text{ rad/s}}^{2}[/latex]. (a) How long does it take to come to rest? (b) How many revolutions does it make before stopping?
  4. During a very quick stop, a car decelerates at [latex]7\text{.}\text{00}{\text{ m/s}}^{2}[/latex]. (a) What is the angular acceleration of its 0.280-m-radius tires, assuming they do not slip on the pavement? (b) How many revolutions do the tires make before coming to rest, given their initial angular velocity is [latex]\text{95}\text{.}0\text{ rad/s}[/latex]? (c) How long does the car take to stop completely? (d) What distance does the car travel in this time? (e) What was the car’s initial velocity? (f) Do the values obtained seem reasonable, considering that this stop happens very quickly?
    The figure shows the left arm of a man with tattoo imprints and wearing a glove. He is circulating a yo-yo toy, which is in mid air and connected by the string to his hand. Some people are standing in the background watching the yo-yo trick.
    Figure 72.3 Yo-yos are amusing toys that display significant physics and are engineered to enhance performance based on physical laws. (credit: Beyond Neon, Flickr)
  5. Everyday application: Suppose a yo-yo has a center shaft that has a 0.250 cm radius and that its string is being pulled. (a) If the string is stationary and the yo-yo accelerates away from it at a rate of [latex]1\text{.}\text{50}{\text{ m/s}}^{2}[/latex], what is the angular acceleration of the yo-yo? (b) What is the angular velocity after 0.750 s if it starts from rest? (c) The outside radius of the yo-yo is 3.50 cm. What is the tangential acceleration of a point on its edge?

Glossary

kinematics of rotational motion
describes the relationships among rotation angle, angular velocity, angular acceleration, and time
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book