"

Kinematics

17 Kinematics in Two Dimensions: An Introduction

Learning Objectives

  • Observe that motion in two dimensions consists of horizontal and vertical components.

  • Understand the independence of horizontal and vertical vectors in two-dimensional motion.

 

A busy traffic intersection in New York showing vehicles moving on the road.
Figure 17.1: Walkers and drivers in a city like New York are rarely able to travel in straight lines to reach their destinations. Instead, they must follow roads and sidewalks, making two-dimensional, zigzagged paths. (credit: Margaret W. Carruthers)

Two-Dimensional Motion: Walking in a City

Suppose you want to walk from one point to another in a city with uniform square blocks, as pictured in Figure 17.2.

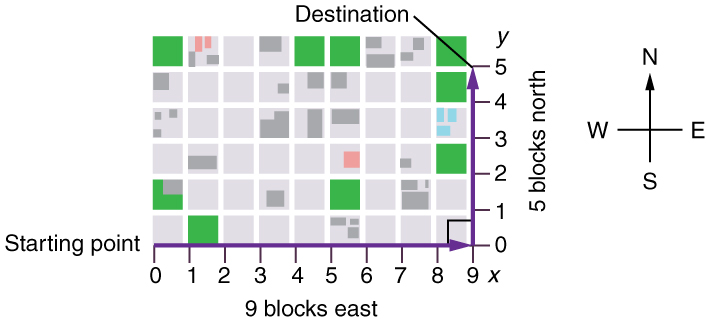
An X Y graph with origin at zero zero with x axis labeled nine blocks east and y axis labeled five blocks north. Starting point at the origin and destination at point nine on the x axis and point five on the y axis.
Figure 17.2: A pedestrian walks a two-dimensional path between two points in a city. In this scene, all blocks are square and are the same size.

The straight-line path a helicopter might fly is blocked to you as a pedestrian, so you must take a two-dimensional path, such as the one shown: 9 blocks east followed by 5 blocks north, totaling 14 blocks walked.

What is the straight-line distance between your start and end points?

An old adage states that the shortest distance between two points is a straight line. Because the two legs of the trip and the straight-line path form a right triangle, the Pythagorean theorem applies:

[latex]{a}^{2} + {b}^{2} = {c}^{2}[/latex]

where [latex]a[/latex] and [latex]b[/latex] are the legs of the triangle, and [latex]c[/latex] is the hypotenuse (the straight-line distance).

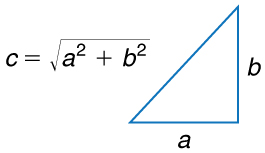
A right-angled triangle with base labeled a height labeled b and hypotenuse labeled c is shown. Using Pythagorean theorem c is calculated as square root of a squared plus b squared.
Figure 17.3: The Pythagorean theorem relates the length of the legs of a right triangle, labeled [latex]a[/latex] and [latex]b[/latex], with the hypotenuse, labeled [latex]c[/latex]. The relationship is given by: [latex]{a}^{2}\text{+ }{b}^{2}\text{= }{c}^{2}[/latex]. This can be rewritten, solving for [latex]c[/latex] : [latex]c\text{ = }\sqrt{{a}^{2}\text{+ }{b}^{2}}[/latex].

Calculating the straight-line distance:

[latex]c = \sqrt{(9\ \text{blocks})^{2} + (5\ \text{blocks})^{2}} = \sqrt{81 + 25} = \sqrt{106} = 10.3\ \text{blocks}[/latex]

This distance is considerably shorter than the 14 blocks you walked.

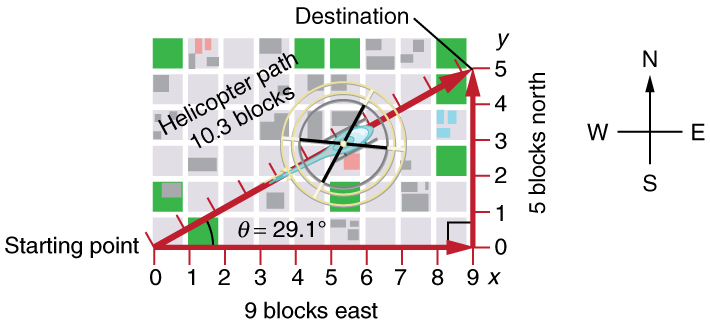
An X Y graph with origin at zero zero with x-axis labeled nine blocks east and y axis labeled five blocks north. A diagonal vector arrow joining starting point at point zero on x axis and destination at point five on y axis with its direction northeast is shown. A helicopter is flying along the diagonal vector arrow with helicopter path of ten point three blocks. The angle formed by diagonal vector arrow and the x-axis is equal to twenty-nine point one degrees.
Figure 17.4: The straight-line path followed by a helicopter between the two points is shorter than the 14 blocks walked by the pedestrian. All blocks are square and the same size.

Vectors and Components

The straight-line distance (magnitude of displacement) being less than the total distance walked exemplifies a general property of vectors—quantities with both magnitude and direction.

In two-dimensional motion, vectors are represented by arrows whose lengths correspond to their magnitudes and point in their directions.

The path of the pedestrian in Figure 17.4 can be represented by three vectors:

  • A 9-block displacement east (horizontal component)

  • A 5-block displacement north (vertical component)

  • The straight-line displacement (resultant vector, 10.3 blocks)

These perpendicular components add vectorially to produce the resultant displacement. The Pythagorean theorem applies only because the components are perpendicular.

The Independence of Perpendicular Motions

The pedestrian’s motion east and north are independent: motion in one direction does not affect motion in the other.

This principle extends to motions where horizontal and vertical components occur simultaneously.

For example, two identical baseballs:

  • One dropped from rest

  • One thrown horizontally from the same height

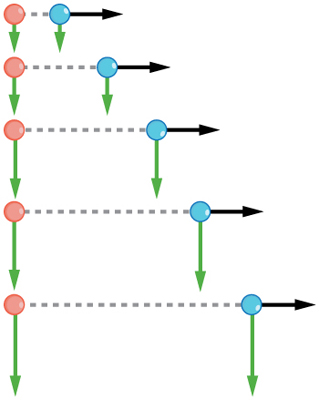
Two identical balls one red and another blue are falling. Five positions of the balls during fall are shown. The horizontal velocity vectors for blue ball towards right are of same magnitude for all the positions. The vertical velocity vectors shown downwards for red ball are increasing with each position.
Figure 17.5:This shows the motions of two identical balls—one falls from rest, the other has an initial horizontal velocity. Each subsequent position is an equal time interval. Arrows represent horizontal and vertical velocities at each position. The ball on the right has an initial horizontal velocity, while the ball on the left has no horizontal velocity. Despite the difference in horizontal velocities, the vertical velocities and positions are identical for both balls. This shows that the vertical and horizontal motions are independent.

The balls’ vertical positions at equal time intervals are the same, proving vertical motion depends only on gravity (ignoring air resistance). The ball thrown horizontally has constant horizontal velocity, unaffected by vertical motion.

PhET Explorations: Ladybug Motion 2D

Learn about position, velocity and acceleration vectors. Move the ladybug by setting the position, velocity or acceleration, and see how the vectors change. Choose linear, circular or elliptical motion, and record and playback the motion to analyze the behavior.

Figure 17.6: Ladybug Motion 2D

Summary

  • Two-dimensional motion can be broken into independent horizontal and vertical components.

  • The Pythagorean theorem applies to find resultant displacement when components are perpendicular.

  • Independence of perpendicular motions allows analyzing complex trajectories like projectile motion by considering each component separately.

Glossary

vector
a quantity that has both magnitude and direction; an arrow used to represent quantities with both magnitude and direction
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book