Rockets come in a wide range of sizes—from small fireworks to the massive Saturn V that carried astronauts toward the Moon. Despite their differences, all rocket engines, including jet engines, balloon propulsion, and even biological examples like squids or octopuses, operate on the same fundamental principle: Newton’s third law of motion. When mass is expelled from a system, the remaining part of the system experiences a force in the opposite direction. A common example of this principle is the recoil of a gun: when a bullet is fired forward, the gun experiences a backward kick.

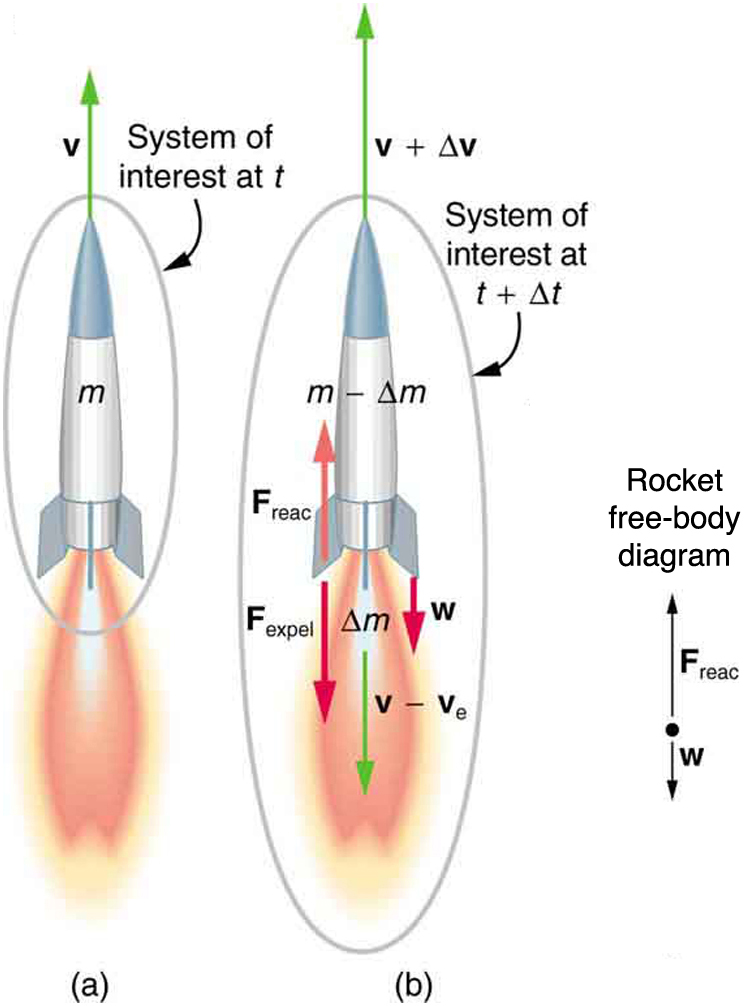
Figure 58.1 shows a rocket accelerating vertically. Initially, the rocket has mass [latex]m[/latex] and moves upward with velocity [latex]v[/latex], giving it momentum [latex]mv[/latex]. After a short time interval [latex]\Delta t[/latex], the rocket ejects a small mass of hot gases [latex]\Delta m[/latex] with exhaust velocity [latex]v_e[/latex] relative to the rocket. The remaining mass [latex]m - \Delta m[/latex] now moves faster, with velocity [latex]v + \Delta v[/latex].

While momentum is approximately conserved in the rocket-gas system, the force of gravity acts during this interval, giving the system a net impulse:

This impulse accounts for a decrease in total momentum, since the center of mass is in free fall. However, the part of the system that remains (the rocket) can still accelerate upward due to the thrust created by ejecting mass.

Contrary to popular belief, a rocket does not require contact with the ground or atmosphere to generate thrust. In fact, rockets are more efficient in space because gases are expelled more freely in a vacuum.

Rocket Acceleration Equation

By analyzing the change in momentum and equating it to impulse, we obtain the rocket’s acceleration as:

Here, [latex]v_e[/latex] is the exhaust velocity of the gas, [latex]m[/latex] is the rocket’s mass at the moment of analysis, [latex]\Delta m[/latex] is the ejected mass, [latex]\Delta t[/latex] is the time interval over which the mass is expelled, and [latex]g[/latex] is the acceleration due to gravity.

Factors Affecting Rocket Acceleration

From the acceleration equation, we can identify three main factors that influence rocket performance:

• Exhaust velocity [latex]v_e[/latex]: A higher exhaust velocity results in greater acceleration.
• Rate of fuel burn [latex]\Delta m / \Delta t[/latex]: Burning fuel faster increases thrust and thus acceleration.
• Rocket mass [latex]m[/latex]: Lower mass increases acceleration. Since rockets lose mass rapidly as they burn fuel, acceleration increases throughout the launch.

To reach the extremely high speeds needed to travel between continents, reach Earth orbit, or escape Earth’s gravity entirely, a rocket must minimize its mass apart from fuel. In other words, the payload, engines, tanks, and structure must weigh as little as possible relative to the fuel. Under idealized conditions (ignoring air resistance and gravity), the final velocity of a single-stage rocket launched from rest can be expressed by the following equation:

Here, [latex]v[/latex] is the final speed (or change in speed), [latex]v_e[/latex] is the exhaust velocity of the ejected gases relative to the rocket, [latex]m_0[/latex] is the initial mass of the rocket (including fuel), and [latex]m_r[/latex] is the remaining mass after the fuel is spent. The term [latex]\ln(m_0/m_r)[/latex] is the natural logarithm of the mass ratio.

Let’s apply this equation to estimate how much fuel is needed to escape Earth’s gravitational pull. Suppose the escape velocity from Earth is [latex]v = 11.2 \times 10^3\ \text{m/s}[/latex], and the exhaust velocity of the rocket is [latex]v_e = 2.5 \times 10^3\ \text{m/s}[/latex]. Then:

Solving for the mass ratio:

So, the remaining mass [latex]m_r[/latex] is:

This result tells us that only 1/88 of the rocket’s initial mass remains after fuel is exhausted. In other words, 87/88 of the initial mass—about 98.9%—was fuel, leaving just 1.1% for the payload, structure, engines, and tanks. When air resistance and gravity are included in the analysis, the required ratio is even more extreme. A realistic estimate suggests the rocket must have a final mass of about [latex]m_0 / 180[/latex] to escape Earth’s gravity. Designing rockets with fuel masses 180 times greater than the payload and hardware is extremely difficult.

The engineering solution to this challenge is the use of multistage rockets. In these designs, each stage contributes to part of the velocity gain and is discarded when empty. The next stage then ignites, carrying less mass and allowing a better fuel-to-payload ratio. Once the rocket reaches space, air resistance becomes negligible, and the efficiency improves dramatically.

The space shuttle was a partially reusable space vehicle that attempted to lower launch costs by incorporating reusable components such as the solid fuel boosters and the orbiter (Figure 58.2). However, because the shuttle was designed for human operation and required complex support systems, it remained expensive compared to unmanned, single-use rockets for satellite launches. Ideally, the shuttle was intended for missions that required human presence, such as satellite repairs or assembling the International Space Station.

Another approach to improving rocket efficiency is launching from airplanes. Doing so provides two major benefits: it avoids most atmospheric drag and gives the rocket an initial boost in velocity, both of which reduce the required fuel.

Section Summary

• According to Newton’s third law of motion, for every action there is an equal and opposite reaction. This principle explains how rockets, jet engines, and even biological systems like squids and octopuses generate propulsion by expelling mass in one direction to move in the opposite direction.
• The acceleration of a rocket under idealized conditions (neglecting air resistance and assuming vertical motion) is given by:
  [latex]a = \frac{v_e}{m} \cdot \frac{\Delta m}{\Delta t} - g[/latex]

  where:

  • [latex]a[/latex] is the rocket’s acceleration
  • [latex]v_e[/latex] is the exhaust velocity of the gases
  • [latex]m[/latex] is the instantaneous mass of the rocket
  • [latex]\Delta m / \Delta t[/latex] is the rate of fuel consumption
  • [latex]g[/latex] is the acceleration due to gravity
• A rocket’s acceleration depends on three primary factors:
  1. Exhaust velocity: Higher exhaust velocity [latex]v_e[/latex] leads to greater thrust and acceleration.
  2. Fuel burn rate: A higher rate of fuel consumption [latex]\Delta m / \Delta t[/latex] increases acceleration.
  3. Rocket mass: Lower total mass [latex]m[/latex] results in greater acceleration for the same thrust.