Linear Momentum and Collisions
56 Inelastic Collisions in One Dimension
Learning Objectives
- Define an inelastic collision and how it differs from an elastic collision.
- Explain the characteristics of a perfectly inelastic collision.
- Apply concepts of momentum conservation to understand collisions in sports and biological systems.
- Calculate recoil velocity and kinetic energy loss given mass and initial velocities.
In previous sections, we saw that an elastic collision is one where both momentum and internal kinetic energy are conserved. However, not all collisions behave this way. An inelastic collision is one in which internal kinetic energy is not conserved. This means some of the system’s kinetic energy is transformed into other forms of energy, such as heat, deformation, or sound.
Inelastic Collision
An inelastic collision is one in which internal kinetic energy changes—it is not conserved. Momentum, however, is still conserved as long as the system is isolated.
In inelastic collisions, internal forces during the impact may do work, converting energy into forms that remain within the system but are no longer associated with bulk motion. For example, when two colliding objects stick together or deform, mechanical energy is transformed into heat or internal vibrations. This process occurs in biological systems as well—for instance, in soft tissue deformation during sports impacts.
Perfectly inelastic collisions (see Figure 56.1) are a special category where the colliding objects stick together after impact. In this case, the system loses the maximum possible amount of internal kinetic energy while still conserving momentum. These types of collisions are useful in modeling events like tackles in football, car crashes, or organ motion against boundaries during blunt force trauma.
Perfectly Inelastic Collision
A perfectly inelastic collision is one in which the objects stick together after the collision. It results in the greatest possible loss of internal kinetic energy while still conserving momentum.
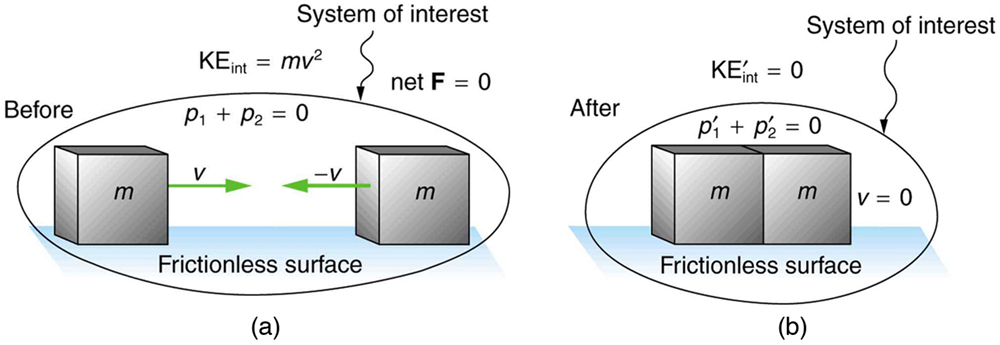
Example 56.1: Calculating Velocity and Change in Kinetic Energy: Inelastic Collision of a Puck and a Goalie
(a) Find the recoil velocity of a 70.0-kg ice hockey goalie, originally at rest, who catches a 0.150-kg hockey puck slapped at him at a velocity of 35.0 m/s. (b) How much kinetic energy is lost during the collision? Assume friction between the ice and the puck-goalie system is negligible. (See Figure 56.2)
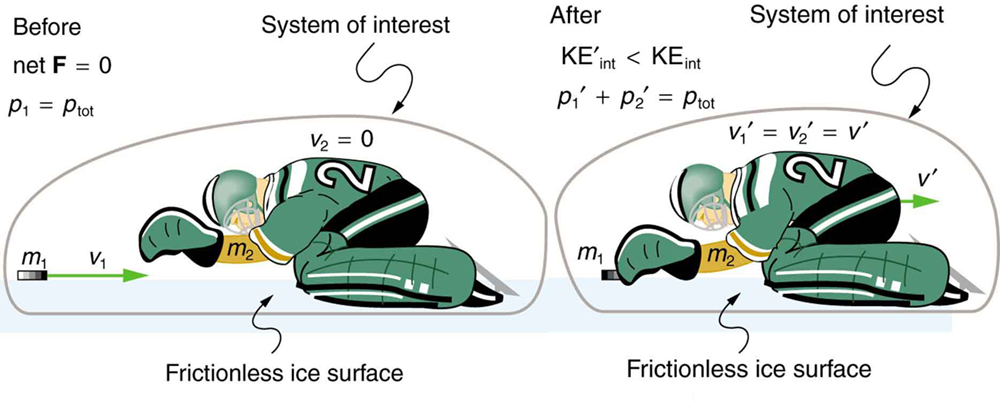
Strategy
Momentum is conserved because the net external force on the puck-goalie system is zero. We can thus use conservation of momentum to find the final velocity of the puck and goalie system. Note that the initial velocity of the goalie is zero and that the final velocity of the puck and goalie are the same. Once the final velocity is found, the kinetic energies can be calculated before and after the collision and compared as requested.
Solution for (a)
Momentum is conserved because the net external force on the puck-goalie system is zero.
Conservation of momentum is
or
Because the goalie is initially at rest, we know [latex]{v}_{2}=0[/latex]. Because the goalie catches the puck, the final velocities are equal, or [latex]{v\prime }_{1}={v\prime }_{2}=v\prime[/latex]. Thus, the conservation of momentum equation simplifies to
Solving for [latex]v\prime[/latex] yields
Entering known values in this equation, we get
Discussion for (a)
This recoil velocity is small and in the same direction as the puck’s original velocity, as we might expect.
Solution for (b)
Before the collision, the internal kinetic energy [latex]{\text{KE}}_{\text{int}}[/latex] of the system is that of the hockey puck, because the goalie is initially at rest. Therefore, [latex]{\text{KE}}_{\text{int}}[/latex] is initially
After the collision, the internal kinetic energy is
The change in internal kinetic energy is thus
where the minus sign indicates that the energy was lost.
Discussion for (b)
Nearly all of the initial internal kinetic energy is lost in this perfectly inelastic collision. [latex]{\text{KE}}_{\text{int}}[/latex] is mostly converted to thermal energy and sound.
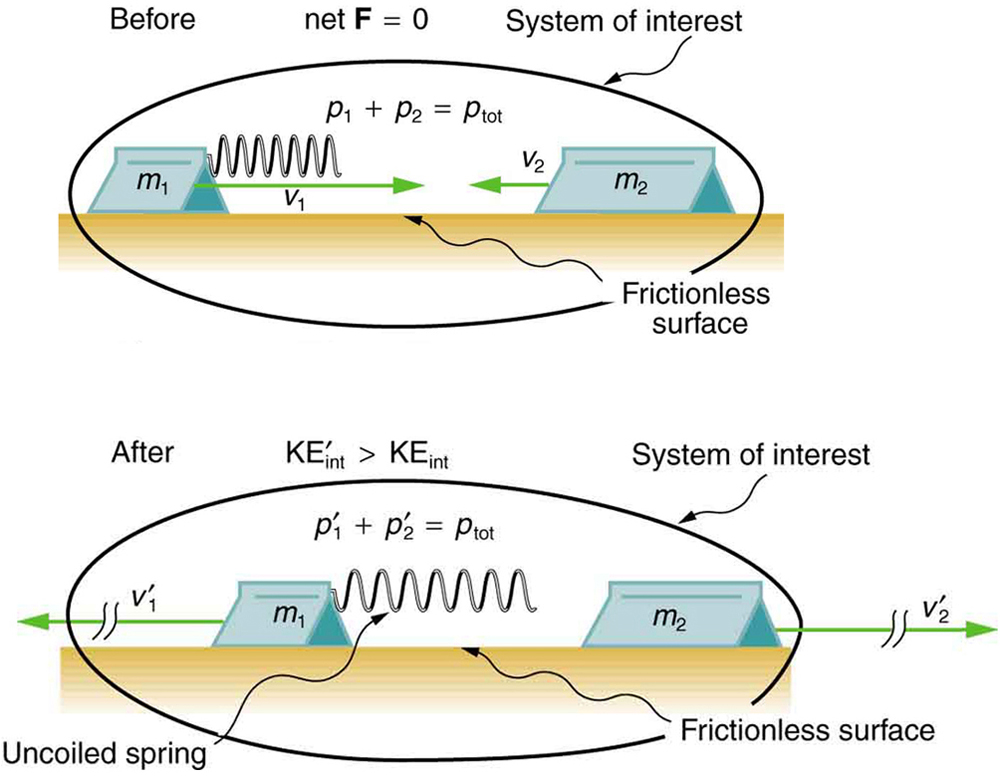
During some collisions, the objects do not stick together and less of the internal kinetic energy is removed—such as happens in most automobile accidents. Alternatively, stored energy may be converted into internal kinetic energy during a collision. Figure 56.3 shows a one-dimensional example in which two carts on an air track collide, releasing potential energy from a compressed spring.
Collisions are particularly important in sports and the sporting and leisure industry utilizes elastic and inelastic collisions. Let us look briefly at tennis. Recall that in a collision, it is momentum and not force that is important. So, a heavier tennis racquet will have the advantage over a lighter one. This conclusion also holds true for other sports—a lightweight bat (such as a softball bat) cannot hit a hardball very far.
The location of the impact of the tennis ball on the racquet is also important, as is the part of the stroke during which the impact occurs. A smooth motion results in the maximizing of the velocity of the ball after impact and reduces sports injuries such as tennis elbow. A tennis player tries to hit the ball on the “sweet spot” on the racquet, where the vibration and impact are minimized and the ball is able to be given more velocity. Sports science and technologies also use physics concepts such as momentum and rotational motion and vibrations.
Take-Home Experiment — Bouncing of a Tennis Ball
This experiment explores how the nature of a surface affects the elasticity of a collision, using a tennis ball and a racquet. You’ll investigate the concept of the coefficient of restitution, a measure of how much kinetic energy remains after a collision.
Materials:
- A tennis ball (or similar rubber ball)
- A racquet (tennis, badminton, or squash racquet)
- A measuring tape or ruler
- A helper (for Part 2)
Part 1: Racquet on the Floor
- Place the racquet flat on the floor with the handle pointing outward.
- Stand on the handle to keep the racquet stationary.
- Hold the tennis ball at a measured height [latex]H[/latex] above the racquet’s strings and drop it.
- Observe and measure the height [latex]h[/latex] to which the ball bounces after impact.
Part 2: Racquet Held in the Hand
- Have a friend hold the racquet firmly by the handle in the air.
- Drop the tennis ball from the same height [latex]H[/latex] as before.
- Again, observe and measure the bounce height [latex]h[/latex].
- Watch what happens to your friend’s hand during the impact. Does it recoil or absorb some of the impact energy?
Analysis: The coefficient of restitution [latex]c[/latex] is a ratio that compares the speed after a collision to the speed before it. For vertical bounces, this can be expressed as:
Where:
- [latex]H[/latex] is the original drop height
- [latex]h[/latex] is the rebound height
Calculate [latex]c[/latex] for both scenarios. Compare your result to the expected coefficient of restitution for a new tennis ball on a hard surface, which is typically:
What differences did you observe between the two setups? How did holding the racquet affect energy transfer and rebound height? Did your friend’s hand absorb part of the momentum? This activity helps connect energy conservation and momentum transfer to real-world collisions seen in sports and biomechanics.
Example 56.2: Calculating Final Velocity and Energy Release: Two Carts Collide
In the collision pictured in Figure 56.3, two carts collide inelastically. Cart 1 (denoted [latex]{m}_{1}[/latex] carries a spring which is initially compressed. During the collision, the spring releases its potential energy and converts it to internal kinetic energy. The mass of cart 1 and the spring is 0.350 kg, and the cart and the spring together have an initial velocity of [latex]2\text{.}\text{00 m/s}[/latex]. Cart 2 (denoted [latex]{m}_{2}[/latex] in Figure 56.3) has a mass of 0.500 kg and an initial velocity of [latex]-0\text{.}\text{500 m/s}[/latex]. After the collision, cart 1 is observed to recoil with a velocity of [latex]-4\text{.}\text{00 m/s}[/latex]. (a) What is the final velocity of cart 2? (b) How much energy was released by the spring (assuming all of it was converted into internal kinetic energy)?
Strategy
We can use conservation of momentum to find the final velocity of cart 2, because [latex]{F}_{\text{net}}=0[/latex] (the track is frictionless and the force of the spring is internal). Once this velocity is determined, we can compare the internal kinetic energy before and after the collision to see how much energy was released by the spring.
Solution for (a)
As before, the equation for conservation of momentum in a two-object system is
The only unknown in this equation is [latex]{v\prime }_{2}[/latex]. Solving for [latex]{v\prime }_{2}[/latex] and substituting known values into the previous equation yields
Solution for (b)
The internal kinetic energy before the collision is
After the collision, the internal kinetic energy is
The change in internal kinetic energy is thus
Discussion
The final velocity of cart 2 is large and positive, meaning that it is moving to the right after the collision. The internal kinetic energy in this collision increases by 5.46 J. That energy was released by the spring.
Section Summary
- An inelastic collision is a type of collision in which internal kinetic energy is not conserved. Some of the energy is transformed into other forms such as heat, sound, or deformation of the objects involved.
- A perfectly inelastic collision occurs when two colliding objects stick together after the collision, resulting in the maximum possible loss of internal kinetic energy while still conserving momentum.
- These principles are not just abstract physics—they have direct applications in health and life sciences. For example, concepts such as momentum, rotational motion, and energy dissipation are critical in sports science, physical therapy, and the design of protective equipment like helmets or joint braces.
Conceptual Questions
- What is an inelastic collision? What is a perfectly inelastic collision?
- Mixed-pair ice skaters performing in a show are standing motionless at arms length just before starting a routine. They reach out, clasp hands, and pull themselves together by only using their arms. Assuming there is no friction between the blades of their skates and the ice, what is their velocity after their bodies meet?
- A small pickup truck that has a camper shell slowly coasts toward a red light with negligible friction. Two dogs in the back of the truck are moving and making various inelastic collisions with each other and the walls. What is the effect of the dogs on the motion of the center of mass of the system (truck plus entire load)? What is their effect on the motion of the truck?
Problems & Exercises
- A 0.240-kg billiard ball that is moving at 3.00 m/s strikes the bumper of a pool table and bounces straight back at 2.40 m/s (80% of its original speed). The collision lasts 0.0150 s. (a) Calculate the average force exerted on the ball by the bumper. (b) How much kinetic energy in joules is lost during the collision? (c) What percent of the original energy is left?
- During an ice show, a 60.0-kg skater leaps into the air and is caught by an initially stationary 75.0-kg skater. (a) What is their final velocity assuming negligible friction and that the 60.0-kg skater’s original horizontal velocity is 4.00 m/s? (b) How much kinetic energy is lost?
- A battleship that is [latex]6\text{.}\text{00}×{\text{10}}^{7}\phantom{\rule{0.25em}{0ex}}\text{kg}[/latex] and is originally at rest fires a 1100-kg artillery shell horizontally with a velocity of 575 m/s. (a) If the shell is fired straight aft (toward the rear of the ship), there will be negligible friction opposing the ship’s recoil. Calculate its recoil velocity. (b) Calculate the increase in internal kinetic energy (that is, for the ship and the shell). This energy is less than the energy released by the gun powder—significant heat transfer occurs.
- Professional Application Two manned satellites approaching one another, at a relative speed of 0.250 m/s, intending to dock. The first has a mass of [latex]4\text{.}\text{00}×{\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}\text{kg}[/latex], and the second a mass of [latex]\text{7.50}×{\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}\text{kg}[/latex]. (a) Calculate the final velocity (after docking) by using the frame of reference in which the first satellite was originally at rest. (b) What is the loss of kinetic energy in this inelastic collision? (c) Repeat both parts by using the frame of reference in which the second satellite was originally at rest. Explain why the change in velocity is different in the two frames, whereas the change in kinetic energy is the same in both.
- Professional Application A 30,000-kg freight car is coasting at 0.850 m/s with negligible friction under a hopper that dumps 110,000 kg of scrap metal into it. (a) What is the final velocity of the loaded freight car? (b) How much kinetic energy is lost?
- Professional Application Space probes may be separated from their launchers by exploding bolts. (They bolt away from one another.) Suppose a 4800-kg satellite uses this method to separate from the 1500-kg remains of its launcher, and that 5000 J of kinetic energy is supplied to the two parts. What are their subsequent velocities using the frame of reference in which they were at rest before separation?
- A 0.0250-kg bullet is accelerated from rest to a speed of 550 m/s in a 3.00-kg rifle. The pain of the rifle’s kick is much worse if you hold the gun loosely a few centimeters from your shoulder rather than holding it tightly against your shoulder. (a) Calculate the recoil velocity of the rifle if it is held loosely away from the shoulder. (b) How much kinetic energy does the rifle gain? (c) What is the recoil velocity if the rifle is held tightly against the shoulder, making the effective mass 28.0 kg? (d) How much kinetic energy is transferred to the rifle-shoulder combination? The pain is related to the amount of kinetic energy, which is significantly less in this latter situation. (e) Calculate the momentum of a 110-kg football player running at 8.00 m/s. Compare the player’s momentum with the momentum of a hard-thrown 0.410-kg football that has a speed of 25.0 m/s. Discuss its relationship to this problem.
- Professional Application One of the waste products of a nuclear reactor is plutonium-239 [latex]\left({}^{\text{239}}\text{Pu}\right)[/latex]. This nucleus is radioactive and decays by splitting into a helium-4 nucleus and a uranium-235 nucleus [latex]\left({}^{4}{\text{He}}^{}+{}^{\text{235}}U\right)[/latex], the latter of which is also radioactive and will itself decay some time later. The energy emitted in the plutonium decay is [latex]\text{8.40}×{\text{10}}^{–\text{13}}\phantom{\rule{0.25em}{0ex}}J[/latex] and is entirely converted to kinetic energy of the helium and uranium nuclei. The mass of the helium nucleus is [latex]\text{6.68}×{\text{10}}^{–\text{27}}\phantom{\rule{0.25em}{0ex}}\text{kg}[/latex], while that of the uranium is [latex]3\text{.}\text{92}×{\text{10}}^{–\text{25}}\phantom{\rule{0.25em}{0ex}}\text{kg}[/latex] (note that the ratio of the masses is 4 to 235). (a) Calculate the velocities of the two nuclei, assuming the plutonium nucleus is originally at rest. (b) How much kinetic energy does each nucleus carry away? Note that the data given here are accurate to three digits only.
- Professional Application The Moon’s craters are remnants of meteorite collisions. Suppose a fairly large asteroid that has a mass of [latex]5\text{.}\text{00}×{10}^{\text{12}}\phantom{\rule{0.25em}{0ex}}\text{kg}[/latex] (about a kilometer across) strikes the Moon at a speed of 15.0 km/s. (a) At what speed does the Moon recoil after the perfectly inelastic collision (the mass of the Moon is [latex]7\text{.}\text{36}×{10}^{\text{22}}\phantom{\rule{0.25em}{0ex}}\text{kg}[/latex]) ? (b) How much kinetic energy is lost in the collision? Such an event may have been observed by medieval English monks who reported observing a red glow and subsequent haze about the Moon. (c) In October 2009, NASA crashed a rocket into the Moon, and analyzed the plume produced by the impact. (Significant amounts of water were detected.) Answer part (a) and (b) for this real-life experiment. The mass of the rocket was 2000 kg and its speed upon impact was 9000 km/h. How does the plume produced alter these results?
- Professional Application Two football players collide head-on in midair while trying to catch a thrown football. The first player is 95.0 kg and has an initial velocity of 6.00 m/s, while the second player is 115 kg and has an initial velocity of –3.50 m/s. What is their velocity just after impact if they cling together?
- What is the speed of a garbage truck that is [latex]1\text{.}\text{20}×{\text{10}}^{4}\phantom{\rule{0.25em}{0ex}}\text{kg}[/latex] and is initially moving at 25.0 m/s just after it hits and adheres to a trash can that is 80.0 kg and is initially at rest?
- During a circus act, an elderly performer thrills the crowd by catching a cannon ball shot at him. The cannon ball has a mass of 10.0 kg and the horizontal component of its velocity is 8.00 m/s when the 65.0-kg performer catches it. If the performer is on nearly frictionless roller skates, what is his recoil velocity?
- (a) During an ice skating performance, an initially motionless 80.0-kg clown throws a fake barbell away. The clown’s ice skates allow her to recoil frictionlessly. If the clown recoils with a velocity of 0.500 m/s and the barbell is thrown with a velocity of 10.0 m/s, what is the mass of the barbell? (b) How much kinetic energy is gained by this maneuver? (c) Where does the kinetic energy come from?
Glossary
- inelastic collision
- a collision in which internal kinetic energy is not conserved
- perfectly inelastic collision
- a collision in which the colliding objects stick together
Learning Objectives
- Define linear momentum.
- Explain the relationship between momentum and force.
- State Newton’s second law of motion in terms of momentum.
- Calculate momentum given mass and velocity.
Linear Momentum
The scientific definition of linear momentum is consistent with most people’s intuitive understanding of momentum: a large, fast-moving object has greater momentum than a smaller, slower object. Linear momentum is defined as the product of a system’s mass multiplied by its velocity. In symbols, linear momentum is expressed as
Momentum is directly proportional to the object’s mass and also its velocity. Thus the greater an object’s mass or the greater its velocity, the greater its momentum. Momentum [latex]\mathbf{p}[/latex] is a vector having the same direction as the velocity [latex]\mathbf{\text{v}}[/latex]. The SI unit for momentum is [latex]\text{kg}·\text{m/s}[/latex].
Linear Momentum
Linear momentum is defined as the product of a system’s mass multiplied by its velocity:
Example 51.1 Calculating Momentum: A Football Player and a Football
(a) Calculate the momentum of a 110-kg football player running at 8.00 m/s. (b) Compare the player’s momentum with the momentum of a hard-thrown 0.410-kg football that has a speed of 25.0 m/s.
Strategy
No information is given regarding direction, and so we can calculate only the magnitude of the momentum, [latex]p[/latex]. (As usual, a symbol that is in italics is a magnitude, whereas one that is italicized, boldfaced, and has an arrow is a vector.) In both parts of this example, the magnitude of momentum can be calculated directly from the definition of momentum given in the equation, which becomes
when only magnitudes are considered.
Solution for (a)
To determine the momentum of the player, substitute the known values for the player’s mass and speed into the equation.
Solution for (b)
To determine the momentum of the ball, substitute the known values for the ball’s mass and speed into the equation.
The ratio of the player’s momentum to that of the ball is
Discussion
Although the ball has greater velocity, the player has a much greater mass. Thus the momentum of the player is much greater than the momentum of the football, as you might guess. As a result, the player’s motion is only slightly affected if he catches the ball. We shall quantify what happens in such collisions in terms of momentum in later sections.
Momentum and Newton’s Second Law
The importance of momentum, unlike the importance of energy, was recognized early in the development of classical physics. Momentum was deemed so important that it was called the “quantity of motion.” Newton actually stated his second law of motion in terms of momentum: The net external force equals the change in momentum of a system divided by the time over which it changes. Using symbols, this law is
where [latex]{\mathbf{F}}_{\text{net}}[/latex] is the net external force, [latex]\Delta \mathbf{p}[/latex] is the change in momentum, and [latex]\Delta t[/latex] is the change in time.
Newton’s Second Law of Motion in Terms of Momentum
The net external force equals the change in momentum of a system divided by the time over which it changes.
Making Connections: Force and Momentum
Force and momentum are intimately related. Force acting over time can change momentum, and Newton’s second law of motion, can be stated in its most broadly applicable form in terms of momentum. Momentum continues to be a key concept in the study of atomic and subatomic particles in quantum mechanics.
This statement of Newton’s second law of motion includes the more familiar [latex]{\mathbf{F}}_{\text{net}}\text{=}m\mathbf{a}[/latex] as a special case. We can derive this form as follows. First, note that the change in momentum [latex]\Delta \mathbf{p}[/latex] is given by
If the mass of the system is constant, then
So that for constant mass, Newton’s second law of motion becomes
Because [latex]\frac{\Delta \mathbf{v}}{\Delta t}=\mathbf{a}[/latex], we get the familiar equation
when the mass of the system is constant.
Newton’s second law of motion stated in terms of momentum is more generally applicable because it can be applied to systems where the mass is changing, such as rockets, as well as to systems of constant mass. We will consider systems with varying mass in some detail; however, the relationship between momentum and force remains useful when mass is constant, such as in the following example.
Example 51.2 Calculating Force: Venus Williams’ Racquet
During the 2007 French Open, Venus Williams hit the fastest recorded serve in a premier women’s match, reaching a speed of 58 m/s (209 km/h). What is the average force exerted on the 0.057-kg tennis ball by Venus Williams’ racquet, assuming that the ball’s speed just after impact is 58 m/s, that the initial horizontal component of the velocity before impact is negligible, and that the ball remained in contact with the racquet for 5.0 ms (milliseconds)?
Strategy
This problem involves only one dimension because the ball starts from having no horizontal velocity component before impact. Newton’s second law stated in terms of momentum is then written as
As noted above, when mass is constant, the change in momentum is given by
In this example, the velocity just after impact and the change in time are given; thus, once [latex]\Delta p[/latex] is calculated, [latex]{F}_{\text{net}}=\frac{\Delta p}{\Delta t}[/latex] can be used to find the force.
Solution
To determine the change in momentum, substitute the values for the initial and final velocities into the equation above.
Now the magnitude of the net external force can determined by using [latex]{F}_{\text{net}}=\frac{\Delta p}{\Delta t}[/latex]:
where we have retained only two significant figures in the final step.
Discussion
This quantity was the average force exerted by Venus Williams’ racquet on the tennis ball during its brief impact (note that the ball also experienced the 0.56-N force of gravity, but that force was not due to the racquet). This problem could also be solved by first finding the acceleration and then using [latex]{F}_{\text{net}}\phantom{\rule{0.15em}{0ex}}\text{=}\phantom{\rule{0.15em}{0ex}}\text{ma}[/latex], but one additional step would be required compared with the strategy used in this example.
Section Summary
- Linear momentum (momentum for brevity) is defined as the product of a system’s mass multiplied by its velocity.
- In symbols, linear momentum [latex]\mathbf{p}[/latex] is defined to be
[latex]\mathbf{p}=m\mathbf{v},[/latex]
where [latex]m[/latex] is the mass of the system and [latex]\mathbf{v}[/latex] is its velocity.
- The SI unit for momentum is [latex]\text{kg}·\text{m/s}[/latex].
- Newton’s second law of motion in terms of momentum states that the net external force equals the change in momentum of a system divided by the time over which it changes.
- In symbols, Newton’s second law of motion is defined to be
[latex]{\mathbf{F}}_{\text{net}}=\frac{\Delta \mathbf{p}}{\Delta t}\text{,}[/latex]
[latex]{\mathbf{F}}_{\text{net}}[/latex] is the net external force, [latex]\Delta \mathbf{p}[/latex] is the change in momentum, and [latex]\Delta t[/latex] is the change time.
Conceptual Questions
- An object that has a small mass and an object that has a large mass have the same momentum. Which object has the largest kinetic energy?
- An object that has a small mass and an object that has a large mass have the same kinetic energy. Which mass has the largest momentum?
- Professional Application Football coaches advise players to block, hit, and tackle with their feet on the ground rather than by leaping through the air. Using the concepts of momentum, work, and energy, explain how a football player can be more effective with his feet on the ground.
- How can a small force impart the same momentum to an object as a large force?
Problems & Exercises
- (a) Calculate the momentum of a 2000-kg elephant charging a hunter at a speed of [latex]7\text{.}\text{50 m/s}[/latex]. (b) Compare the elephant’s momentum with the momentum of a 0.0400-kg tranquilizer dart fired at a speed of [latex]\text{600 m/s}[/latex]. (c) What is the momentum of the 90.0-kg hunter running at [latex]7\text{.}\text{40 m/s}[/latex] after missing the elephant?
- (a) What is the mass of a large ship that has a momentum of [latex]1\text{.}\text{60}×{\text{10}}^{9}\phantom{\rule{0.25em}{0ex}}\text{kg}·\text{m/s}[/latex], when the ship is moving at a speed of [latex]\text{48.0 km/h?}[/latex] (b) Compare the ship’s momentum to the momentum of a 1100-kg artillery shell fired at a speed of [latex]\text{1200 m/s}[/latex].
- (a) At what speed would a [latex]2\text{.}\text{00}×{\text{10}}^{4}\text{-kg}[/latex] airplane have to fly to have a momentum of [latex]1\text{.}\text{60}×{\text{10}}^{9}\phantom{\rule{0.25em}{0ex}}\text{kg}·\text{m/s}[/latex] (the same as the ship’s momentum in the problem above)? (b) What is the plane’s momentum when it is taking off at a speed of [latex]\text{60.0 m/s}[/latex]? (c) If the ship is an aircraft carrier that launches these airplanes with a catapult, discuss the implications of your answer to (b) as it relates to recoil effects of the catapult on the ship.
- (a) What is the momentum of a garbage truck that is [latex]1\text{.}\text{20}×{\text{10}}^{4}\phantom{\rule{0.25em}{0ex}}\text{kg}[/latex] and is moving at [latex]10\text{.}\text{0 m/s}[/latex]? (b) At what speed would an 8.00-kg trash can have the same momentum as the truck?
- A runaway train car that has a mass of 15,000 kg travels at a speed of [latex]5\text{.4 m/s}[/latex] down a track. Compute the time required for a force of 1500 N to bring the car to rest.
- The mass of Earth is [latex]5\text{.}\text{972}×{10}^{\text{24}}\phantom{\rule{0.25em}{0ex}}\text{kg}[/latex] and its orbital radius is an average of [latex]1\text{.}\text{496}×{10}^{\text{11}}\phantom{\rule{0.25em}{0ex}}\text{m}[/latex]. Calculate its linear momentum.
Glossary
- linear momentum
- the product of mass and velocity
- second law of motion
- physical law that states that the net external force equals the change in momentum of a system divided by the time over which it changes
Learning Objectives
- Describe the principle of conservation of momentum.
- Derive an expression for the conservation of momentum.
- Explain conservation of momentum with examples.
- Explain the principle of conservation of momentum as it relates to atomic and subatomic particles.
Momentum is an important quantity because it is conserved. Yet it was not conserved in the examples in Impulse and Linear Momentum and Force, where large changes in momentum were produced by forces acting on the system of interest. Under what circumstances is momentum conserved?
The answer to this question entails considering a sufficiently large system. It is always possible to find a larger system in which total momentum is constant, even if momentum changes for components of the system. If a football player runs into the goalpost in the end zone, there will be a force on him that causes him to bounce backward. However, the Earth also recoils —conserving momentum—because of the force applied to it through the goalpost. Because Earth is many orders of magnitude more massive than the player, its recoil is immeasurably small and can be neglected in any practical sense, but it is real nevertheless.
Consider what happens if the masses of two colliding objects are more similar than the masses of a football player and Earth—for example, one car bumping into another, as shown in Figure 53.1. Both cars are coasting in the same direction when the lead car (labeled [latex]{m}_{2}[/latex]) is bumped by the trailing car (labeled [latex]{m}_{1}[/latex]). The only unbalanced force on each car is the force of the collision. (Assume that the effects due to friction are negligible.) Car 1 slows down as a result of the collision, losing some momentum, while car 2 speeds up and gains some momentum. We shall now show that the total momentum of the two-car system remains constant.
Using the definition of impulse, the change in momentum of car 1 is given by
where [latex]{F}_{1}[/latex] is the force on car 1 due to car 2, and [latex]\Delta t[/latex] is the time the force acts (the duration of the collision). Intuitively, it seems obvious that the collision time is the same for both cars, but it is only true for objects traveling at ordinary speeds. This assumption must be modified for objects travelling near the speed of light, without affecting the result that momentum is conserved.
Similarly, the change in momentum of car 2 is
where [latex]{F}_{2}[/latex] is the force on car 2 due to car 1, and we assume the duration of the collision [latex]\Delta t[/latex] is the same for both cars. We know from Newton’s third law that [latex]{F}_{2}=\phantom{\rule{0.25em}{0ex}}–{F}_{1}[/latex], and so
Thus, the changes in momentum are equal and opposite, and
Because the changes in momentum add to zero, the total momentum of the two-car system is constant. That is,
where [latex]{p\prime }_{1}[/latex] and [latex]{p\prime }_{2}[/latex] are the momenta of cars 1 and 2 after the collision. (We often use primes to denote the final state.)
This result—that momentum is conserved—has validity far beyond the preceding one-dimensional case. It can be similarly shown that total momentum is conserved for any isolated system, with any number of objects in it. In equation form, the conservation of momentum principle for an isolated system is written
or
where [latex]{\mathbf{p}}_{\text{tot}}[/latex] is the total momentum (the sum of the momenta of the individual objects in the system) and [latex]{\mathbf{\text{p}}\prime }_{\text{tot}}[/latex] is the total momentum some time later. (The total momentum can be shown to be the momentum of the center of mass of the system.) An isolated system is defined to be one for which the net external force is zero [latex]({\mathbf{\text{F}}}_{\text{net}}=0)\text{.}[/latex]
Conservation of Momentum Principle
Isolated System
An isolated system is defined to be one for which the net external force is zero [latex]({\mathbf{\text{F}}}_{\text{net}}=0)\text{.}[/latex]
Perhaps an easier way to see that momentum is conserved for an isolated system is to consider Newton’s second law in terms of momentum, [latex]{\mathbf{F}}_{\text{net}}=\frac{{\Delta \mathbf{p}}_{\text{tot}}}{\Delta t}[/latex]. For an isolated system,
[latex]({\mathbf{\text{F}}}_{\text{net}}=0)[/latex]; thus, [latex]\Delta {\mathbf{p}}_{\text{tot}}=0[/latex], and
[latex]{\mathbf{p}}_{\text{tot}}[/latex] is constant.
We have noted that the three length dimensions in nature—[latex]x[/latex], [latex]y[/latex], and [latex]z[/latex]—are independent, and it is interesting to note that momentum can be conserved in different ways along each dimension. For example, during projectile motion and where air resistance is negligible, momentum is conserved in the horizontal direction because horizontal forces are zero and momentum is unchanged. But along the vertical direction, the net vertical force is not zero and the momentum of the projectile is not conserved. (See Figure 53.2.) However, if the momentum of the projectile-Earth system is considered in the vertical direction, we find that the total momentum is conserved.
The conservation of momentum principle can be applied to systems as different as a comet striking Earth and a gas containing huge numbers of atoms and molecules. Conservation of momentum is violated only when the net external force is not zero. But another larger system can always be considered in which momentum is conserved by simply including the source of the external force. For example, in the collision of two cars considered above, the two-car system conserves momentum while each one-car system does not.
Making Connections: Take-Home Investigation—Drop of Tennis Ball and a Basketball
Hold a tennis ball side by side and in contact with a basketball. Drop the balls together. (Be careful!) What happens? Explain your observations. Now hold the tennis ball above and in contact with the basketball. What happened? Explain your observations. What do you think will happen if the basketball ball is held above and in contact with the tennis ball?
Making Connections: Take-Home Investigation—Two Tennis Balls in a Ballistic Trajectory
Tie two tennis balls together with a string about a foot long. Hold one ball and let the other hang down and throw it in a ballistic trajectory. Explain your observations. Now mark the center of the string with bright ink or attach a brightly colored sticker to it and throw again. What happened? Explain your observations.
Some aquatic animals such as jellyfish move around based on the principles of conservation of momentum. A jellyfish fills its umbrella section with water and then pushes the water out resulting in motion in the opposite direction to that of the jet of water. Squids propel themselves in a similar manner but, in contrast with jellyfish, are able to control the direction in which they move by aiming their nozzle forward or backward. Typical squids can move at speeds of 8 to 12 km/h.
The ballistocardiograph (BCG) was a diagnostic tool used in the second half of the 20th century to study the strength of the heart. About once a second, your heart beats, forcing blood into the aorta. A force in the opposite direction is exerted on the rest of your body (recall Newton’s third law). A ballistocardiograph is a device that can measure this reaction force. This measurement is done by using a sensor (resting on the person) or by using a moving table suspended from the ceiling. This technique can gather information on the strength of the heart beat and the volume of blood passing from the heart. However, the electrocardiogram (ECG or EKG) and the echocardiogram (cardiac ECHO or ECHO; a technique that uses ultrasound to see an image of the heart) are more widely used in the practice of cardiology.
Making Connections: Conservation of Momentum and Collision
Conservation of momentum is quite useful in describing collisions. Momentum is crucial to our understanding of atomic and subatomic particles because much of what we know about these particles comes from collision experiments.
Subatomic Collisions and Momentum
The conservation of momentum principle not only applies to the macroscopic objects, it is also essential to our explorations of atomic and subatomic particles. Giant machines hurl subatomic particles at one another, and researchers evaluate the results by assuming conservation of momentum (among other things).
On the small scale, we find that particles and their properties are invisible to the naked eye but can be measured with our instruments, and models of these subatomic particles can be constructed to describe the results. Momentum is found to be a property of all subatomic particles including massless particles such as photons that compose light. Momentum being a property of particles hints that momentum may have an identity beyond the description of an object’s mass multiplied by the object’s velocity. Indeed, momentum relates to wave properties and plays a fundamental role in what measurements are taken and how we take these measurements. Furthermore, we find that the conservation of momentum principle is valid when considering systems of particles. We use this principle to analyze the masses and other properties of previously undetected particles, such as the nucleus of an atom and the existence of quarks that make up particles of nuclei. (Figure) below illustrates how a particle scattering backward from another implies that its target is massive and dense. Experiments seeking evidence that quarks make up protons (one type of particle that makes up nuclei) scattered high-energy electrons off of protons (nuclei of hydrogen atoms). Electrons occasionally scattered straight backward in a manner that implied a very small and very dense particle makes up the proton—this observation is considered nearly direct evidence of quarks. The analysis was based partly on the same conservation of momentum principle that works so well on the large scale.
Section Summary
- The conservation of momentum principle is written
[latex]{\mathbf{p}}_{\text{tot}}=\text{constant}[/latex]
or
[latex]{\mathbf{\text{p}}}_{\text{tot}}={\mathbf{\text{p}}\prime }_{\text{tot}}\phantom{\rule{0.25em}{0ex}}\phantom{\rule{0.25em}{0ex}}(\text{isolated system}),[/latex][latex]{\mathbf{p}}_{\text{tot}}[/latex] is the initial total momentum and [latex]{\mathbf{\text{p}}\prime }_{\text{tot}}[/latex] is the total momentum some time later.
- An isolated system is defined to be one for which the net external force is zero [latex]({\mathbf{\text{F}}}_{\text{net}}=0)\text{.}[/latex]
- During projectile motion and where air resistance is negligible, momentum is conserved in the horizontal direction because horizontal forces are zero.
- Conservation of momentum applies only when the net external force is zero.
- The conservation of momentum principle is valid when considering systems of particles.
Conceptual Questions
- Professional Application If you dive into water, you reach greater depths than if you do a belly flop. Explain this difference in depth using the concept of conservation of energy. Explain this difference in depth using what you have learned in this chapter.
- Under what circumstances is momentum conserved?
- Can momentum be conserved for a system if there are external forces acting on the system? If so, under what conditions? If not, why not?
- Momentum for a system can be conserved in one direction while not being conserved in another. What is the angle between the directions? Give an example.
- Professional Application Explain in terms of momentum and Newton’s laws how a car’s air resistance is due in part to the fact that it pushes air in its direction of motion.
- Can objects in a system have momentum while the momentum of the system is zero? Explain your answer.
- Must the total energy of a system be conserved whenever its momentum is conserved? Explain why or why not.
Problems & Exercises
- Professional Application Train cars are coupled together by being bumped into one another. Suppose two loaded train cars are moving toward one another, the first having a mass of 150,000 kg and a velocity of 0.300 m/s, and the second having a mass of 110,000 kg and a velocity of [latex]-0\text{.}\text{120 m/s}[/latex]. (The minus indicates direction of motion.) What is their final velocity?
- Suppose a clay model of a koala bear has a mass of 0.200 kg and slides on ice at a speed of 0.750 m/s. It runs into another clay model, which is initially motionless and has a mass of 0.350 kg. Both being soft clay, they naturally stick together. What is their final velocity
- Professional Application Consider the following question: A car moving at 10 m/s crashes into a tree and stops in 0.26 s. Calculate the force the seatbelt exerts on a passenger in the car to bring him to a halt. The mass of the passenger is 70 kg. Would the answer to this question be different if the car with the 70-kg passenger had collided with a car that has a mass equal to and is traveling in the opposite direction and at the same speed? Explain your answer.
- In a collision with an identical car, momentum is conserved. Afterwards [latex]{v}_{\text{f}}=0[/latex] for both cars. The change in momentum will be the same as in the crash with the tree. However, the force on the body is not determined since the time is not known. A padded stop will reduce injurious force on body.
- What is the velocity of a 900-kg car initially moving at 30.0 m/s, just after it hits a 150-kg deer initially running at 12.0 m/s in the same direction? Assume the deer remains on the car.
- A 1.80-kg falcon catches a 0.650-kg dove from behind in midair. What is their velocity after impact if the falcon’s velocity is initially 28.0 m/s and the dove’s velocity is 7.00 m/s in the same direction?
Glossary
- conservation of momentum principle
- when the net external force is zero, the total momentum of the system is conserved or constant
- isolated system
- a system in which the net external force is zero
- quark
- fundamental constituent of matter and an elementary particle
a collision in which internal kinetic energy is not conserved
a collision in which the colliding objects stick together
