Linear Momentum and Collisions
53 Impulse
Learning Objectives
- Define impulse.
- Describe the role of impulse in real-life scenarios including injury prevention.
- Interpret impulse from force-time graphs.
- Calculate impulse and average force given mass, velocity, and contact time.
When a force is applied to an object, its effect depends not only on the size of the force but also on the duration of time it acts. In biological and medical contexts—such as sports injuries or vehicle collisions—the duration of impact is just as critical as the force itself. A powerful force acting over a short time can cause just as much change in momentum as a smaller force acting over a longer period.
In Example 52.2 a very large force acting for a short time had a great effect on the momentum of the tennis ball. For example, when a tennis racket strikes a ball, the force is large but brief. That same change in the ball’s momentum could be achieved by gently tossing the ball upward and letting gravity slowly reverse its direction. What matters is the product of force and time—this product is called impulse, and it equals the change in momentum:
This equation is a rearranged form of Newton’s second law expressed in terms of momentum:
Example 53.1: Calculating Magnitudes of Impulses: Two Billiard Balls Striking a Rigid Wall
Two identical billiard balls strike a rigid wall with the same speed, and are reflected without any change of speed. The first ball strikes perpendicular to the wall. The second ball strikes the wall at an angle of [latex]\text{30º}[/latex] from the perpendicular, and bounces off at an angle of [latex]\text{30º}[/latex] from perpendicular to the wall.
(a) Determine the direction of the force on the wall due to each ball.
(b) Calculate the ratio of the magnitudes of impulses on the two balls by the wall.
Strategy for (a)
In order to determine the force on the wall, consider the force on the ball due to the wall using Newton’s second law and then apply Newton’s third law to determine the direction. Assume the [latex]x[/latex]-axis to be normal to the wall and to be positive in the initial direction of motion. Choose the [latex]y[/latex]-axis to be along the wall in the plane of the second ball’s motion. The momentum direction and the velocity direction are the same.
Solution for (a)
The first ball bounces directly into the wall and exerts a force on it in the [latex]+x[/latex] direction. Therefore the wall exerts a force on the ball in the [latex]-x[/latex] direction. The second ball continues with the same momentum component in the [latex]y[/latex] direction, but reverses its [latex]x[/latex]-component of momentum, as seen by sketching a diagram of the angles involved and keeping in mind the proportionality between velocity and momentum.
These changes mean the change in momentum for both balls is in the [latex]-x[/latex] direction, so the force of the wall on each ball is along the [latex]-x[/latex] direction.
Strategy for (b)
Calculate the change in momentum for each ball, which is equal to the impulse imparted to the ball.
Solution for (b)
Let [latex]u[/latex] be the speed of each ball before and after collision with the wall, and [latex]m[/latex] the mass of each ball. Choose the [latex]x[/latex]-axis and [latex]y[/latex]-axis as previously described, and consider the change in momentum of the first ball which strikes perpendicular to the wall.
Impulse is the change in momentum vector. Therefore the [latex]x[/latex]-component of impulse is equal to [latex]-2\text{mu}[/latex] and the [latex]y[/latex]-component of impulse is equal to zero.
Now consider the change in momentum of the second ball.
It should be noted here that while [latex]{p}_{x}[/latex] changes sign after the collision, [latex]{p}_{y}[/latex] does not. Therefore the [latex]x[/latex]-component of impulse is equal to [latex]-2\text{mu}\phantom{\rule{0.25em}{0ex}}\text{cos 30º}[/latex] and the [latex]y[/latex]-component of impulse is equal to zero.
The ratio of the magnitudes of the impulse imparted to the balls is
Discussion
The direction of impulse and force is the same as in the case of (a); it is normal to the wall and along the negative [latex]x[/latex]–direction. Making use of Newton’s third law, the force on the wall due to each ball is normal to the wall along the positive [latex]x[/latex] -direction.
Our definition of impulse assumes that the applied force remains constant over the interval [latex]\Delta t[/latex]. However, in real-world scenarios—especially in biomechanics and human motion—forces are rarely constant. Instead, they often vary rapidly over short durations, such as when your foot strikes the ground while running, or when a bat hits a baseball.
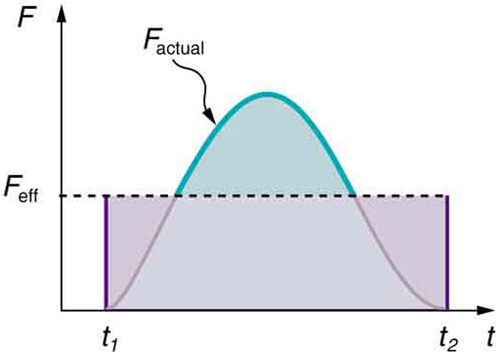
To account for these situations, we introduce an effective average force, denoted [latex]F_{\text{eff}}[/latex], that would produce the same impulse as the actual time-varying force. Figure 53.1 illustrates this concept. The curved line represents the actual varying force exerted over time during an event (such as a ball bouncing). The area under this curve—representing impulse—is equivalent to the area of a rectangle under the constant effective force [latex]F_{\text{eff}}[/latex] over the same time interval [latex]t_2 - t_1[/latex].
Making Connections: Take-Home Investigation—Hand Movement and Impulse
Try this experiment at home to explore how impulse works in your own body. First, catch a soft ball while moving your hands backward as you receive it (sometimes called “giving” with the ball). Then, repeat but keep your hands rigid. Next, hit water in a tub flat-handed and observe the splash. After the water settles, dive your hand in fingers-first. (The flat palm represents a belly flop; fingers-first resembles a proper dive.)
What differences do you notice in force and discomfort? Which motions reduce peak force, and why? These observations show how spreading force over time reduces its damaging effects—critical for athletes, caregivers, and engineers alike.
Making Connections: Constant Force and Constant Acceleration
Using an average or effective force in impulse calculations is conceptually similar to how we often use constant acceleration in kinematics—even though real-world acceleration often changes. In both cases, we apply simplified models that allow us to analyze motion and forces without needing calculus.
For example, in biomechanics or clinical gait analysis, acceleration may vary slightly with each stride. However, treating acceleration as constant can still yield useful insights into speed, stride length, or joint forces—just as average effective force can help us estimate changes in momentum in a collision.
This kind of approximation is both practical and powerful. It enables us to understand complex biological motion and mechanical processes while keeping the math manageable and the concepts clear.
Section Summary
- Impulse—or change in momentum—is equal to the average net external force times the time interval over which the force acts:
[latex]\Delta \mathbf{p} = \mathbf{F}_{\text{net}} \Delta t[/latex]
- In real-world interactions, forces are usually not constant over time.
- An average effective force can be used to simplify calculations while still yielding the correct impulse.
Conceptual Questions
- Professional Application Explain in terms of impulse how padding reduces forces in a collision. State this in terms of a real example, such as the advantages of a carpeted vs. tile floor for a day care center.
- While jumping on a trampoline, sometimes you land on your back and other times on your feet. In which case can you reach a greater height and why?
- Professional Application Tennis racquets have “sweet spots.” If the ball hits a sweet spot then the player’s arm is not jarred as much as it would be otherwise. Explain why this is the case.
Problems & Exercises
- A bullet is accelerated down the barrel of a gun by hot gases produced in the combustion of gun powder. What is the average force exerted on a 0.0300-kg bullet to accelerate it to a speed of 600 m/s in a time of 2.00 ms (milliseconds)?
- Professional Application A car moving at 10 m/s crashes into a tree and stops in 0.26 s. Calculate the force the seat belt exerts on a passenger in the car to bring him to a halt. The mass of the passenger is 70 kg.
- A person slaps her leg with her hand, bringing her hand to rest in 2.50 milliseconds from an initial speed of 4.00 m/s. (a) What is the average force exerted on the leg, taking the effective mass of the hand and forearm to be 1.50 kg? (b) Would the force be any different if the woman clapped her hands together at the same speed and brought them to rest in the same time? Explain why or why not.
- Professional Application A professional boxer hits his opponent with a 1000-N horizontal blow that lasts for 0.150 s. (a) Calculate the impulse imparted by this blow. (b) What is the opponent’s final velocity, if his mass is 105 kg and he is motionless in midair when struck near his center of mass? (c) Calculate the recoil velocity of the opponent’s 10.0-kg head if hit in this manner, assuming the head does not initially transfer significant momentum to the boxer’s body. (d) Discuss the implications of your answers for parts (b) and (c).
- Professional Application Suppose a child drives a bumper car head on into the side rail, which exerts a force of 4000 N on the car for 0.200 s. (a) What impulse is imparted by this force? (b) Find the final velocity of the bumper car if its initial velocity was 2.80 m/s and the car plus driver have a mass of 200 kg. You may neglect friction between the car and floor.
- Professional Application One hazard of space travel is debris left by previous missions. There are several thousand objects orbiting Earth that are large enough to be detected by radar, but there are far greater numbers of very small objects, such as flakes of paint. Calculate the force exerted by a 0.100-mg chip of paint that strikes a spacecraft window at a relative speed of [latex]4\text{.}\text{00}×{\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}\text{m/s}[/latex], given the collision lasts [latex]6\text{.}\text{00}×{\text{10}}^{–8}\phantom{\rule{0.25em}{0ex}}s[/latex].
- Professional Application A 75.0-kg person is riding in a car moving at 20.0 m/s when the car runs into a bridge abutment. (a) Calculate the average force on the person if he is stopped by a padded dashboard that compresses an average of 1.00 cm. (b) Calculate the average force on the person if he is stopped by an air bag that compresses an average of 15.0 cm.
- Professional Application Military rifles have a mechanism for reducing the recoil forces of the gun on the person firing it. An internal part recoils over a relatively large distance and is stopped by damping mechanisms in the gun. The larger distance reduces the average force needed to stop the internal part. (a) Calculate the recoil velocity of a 1.00-kg plunger that directly interacts with a 0.0200-kg bullet fired at 600 m/s from the gun. (b) If this part is stopped over a distance of 20.0 cm, what average force is exerted upon it by the gun? (c) Compare this to the force exerted on the gun if the bullet is accelerated to its velocity in 10.0 ms (milliseconds).
- A cruise ship with a mass of [latex]1\text{.}\text{00}×{\text{10}}^{7}\phantom{\rule{0.25em}{0ex}}\text{kg}[/latex] strikes a pier at a speed of 0.750 m/s. It comes to rest 6.00 m later, damaging the ship, the pier, and the tugboat captain’s finances. Calculate the average force exerted on the pier using the concept of impulse. (Hint: First calculate the time it took to bring the ship to rest.)
- Calculate the final speed of a 110-kg rugby player who is initially running at 8.00 m/s but collides head-on with a padded goalpost and experiences a backward force of [latex]1\text{.}\text{76}×{\text{10}}^{4}\phantom{\rule{0.25em}{0ex}}\text{N}[/latex] for [latex]5\text{.}\text{50}×{\text{10}}^{\text{–2}}\phantom{\rule{0.25em}{0ex}}\text{s}[/latex].
- Water from a fire hose is directed horizontally against a wall at a rate of 50.0 kg/s and a speed of 42.0 m/s. Calculate the magnitude of the force exerted on the wall, assuming the water’s horizontal momentum is reduced to zero.
- A 0.450-kg hammer is moving horizontally at 7.00 m/s when it strikes a nail and comes to rest after driving the nail 1.00 cm into a board. (a) Calculate the duration of the impact. (b) What was the average force exerted on the nail?
- Starting with the definitions of momentum and kinetic energy, derive an equation for the kinetic energy of a particle expressed as a function of its momentum.
- A ball with an initial velocity of 10 m/s moves at an angle [latex]\text{60º}[/latex] above the [latex]+x[/latex]-direction. The ball hits a vertical wall and bounces off so that it is moving [latex]\text{60º}[/latex] above the [latex]-x[/latex]-direction with the same speed. What is the impulse delivered by the wall?
- When serving a tennis ball, a player hits the ball when its velocity is zero (at the highest point of a vertical toss). The racquet exerts a force of 540 N on the ball for 5.00 ms, giving it a final velocity of 45.0 m/s. Using these data, find the mass of the ball.
- A punter drops a ball from rest vertically 1 meter down onto his foot. The ball leaves the foot with a speed of 18 m/s at an angle [latex]\text{55º}[/latex] above the horizontal. What is the impulse delivered by the foot (magnitude and direction)?
Glossary
- change in momentum
- the difference between the final and initial momentum; the mass times the change in velocity
- impulse
- the average net external force times the time it acts; equal to the change in momentum
the difference between the final and initial momentum; the mass times the change in velocity
the average net external force times the time it acts; equal to the change in momentum

