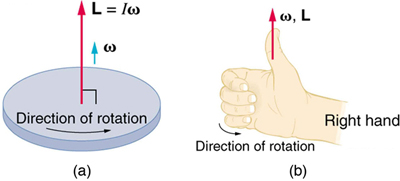
Angular momentum is a vector and, therefore, has direction as well as magnitude. Torque affects both the direction and the magnitude of angular momentum. What is the direction of the angular momentum of a rotating object like the disk in Figure 68.1? The figure shows the right-hand rule used to find the direction of both angular momentum and angular velocity. Both [latex]\mathbf{L}[/latex] and [latex]\mathbf{\omega}[/latex] are vectors—each has direction and magnitude. Both can be represented by arrows. The right-hand rule defines both to be perpendicular to the plane of rotation in the direction shown. Because angular momentum is related to angular velocity by

the direction of [latex]\mathbf{L}[/latex] is the same as the direction of [latex]\mathbf{\omega}[/latex]. Notice in the figure that both point along the axis of rotation.

Now, recall that torque changes angular momentum as expressed by:

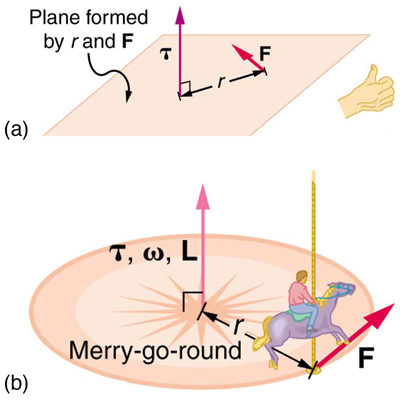
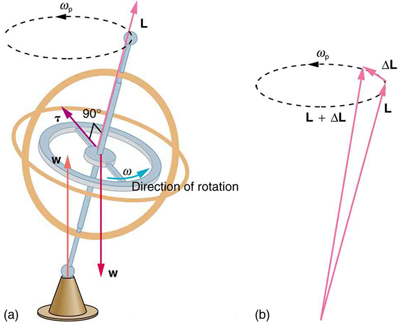
This equation means that the direction of [latex]\Delta \mathbf{L}[/latex] is the same as the direction of the torque [latex]\mathbf{\tau}[/latex] that creates it. This result is illustrated in Figure 68.2, which shows the direction of torque and the angular momentum it creates.

Let us now consider a bicycle wheel with a couple of handles attached to it, as shown in Figure 68.3. This device is popular in physics demos because it does unexpected things. With the wheel rotating as shown, its angular momentum is to the woman’s left. If she tries to rotate the wheel by applying forces, those forces create a torque that is horizontal toward her. This torque changes [latex]\mathbf{L}[/latex] in the same direction, perpendicular to the original [latex]\mathbf{L}[/latex], thus altering the direction of [latex]\mathbf{L}[/latex] but not its magnitude. The axis of the wheel moves perpendicular to the applied forces, not in the expected direction.

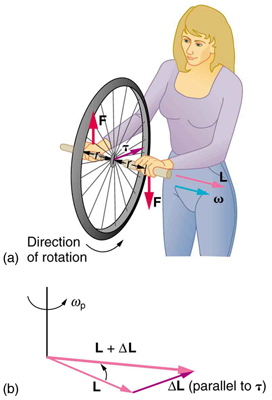
This same logic explains the behavior of gyroscopes. Figure 68.4 shows the two forces acting on a spinning gyroscope. The torque produced is perpendicular to [latex]\mathbf{L}[/latex], changing its direction but not magnitude. The gyroscope precesses around a vertical axis due to the horizontal torque. If the gyroscope is not spinning, it gains angular momentum in the direction of the torque and falls over.

Earth acts like a gigantic gyroscope. Its angular momentum vector points along its rotation axis toward Polaris, the North Star. However, due to torque from the Sun and Moon acting on its oblate shape, Earth precesses slowly—once every ~26,000 years.

Problem Exercises

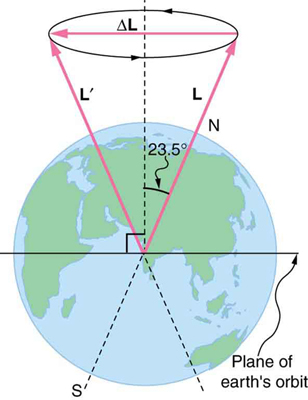
5. Integrated Concepts The axis of Earth makes a 23.5° angle with a direction perpendicular to the plane of Earth’s orbit. As shown in Figure 68.5, this axis precesses, making one complete rotation in 25,780 y. (a) Calculate the change in angular momentum in half this time. (b) What is the average torque producing this change in angular momentum? (c) If this torque were created by a single force (it is not) acting at the most effective point on the equator, what would its magnitude be?