Gravitational Potential Energy

Saul Beceiro-Novo

Work, Energy, and Energy Resources

44 Gravitational Potential Energy

Learning Objectives

Explain gravitational potential energy in terms of work done against gravity.
Show that the gravitational potential energy of an object of mass $m$ at height $h$ is given by ${PE}_{g} = mgh$ .
Use gravitational potential energy as a function of position to simplify physical calculations.

Work Done Against Gravity

Lifting an object—whether it’s a textbook, a patient in a hospital bed, or a box of medical supplies—requires work. In physics, work is done when a force is applied to move an object over a distance, and this includes work done against gravity. When we lift an object, we increase its gravitational potential energy, a form of energy associated with the position of an object relative to Earth.

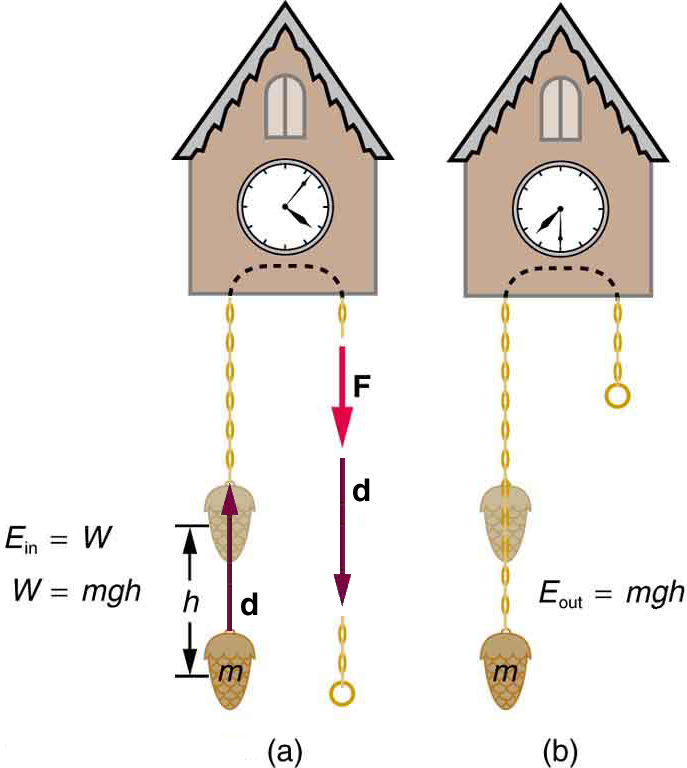
Consider lifting an object of mass $m$ vertically through a height $h$ , as shown in Figure 43.1(a). If the object moves at constant speed, the upward force must equal the object’s weight, $F = m g$ . The work done is:

$W = F d = m g h .$

This work becomes stored energy—gravitational potential energy, or ${PE}_{g}$ . We define this energy as:

${PE}_{g} = m g h .$

It’s important to note that gravitational potential energy is a property of a system, specifically the Earth-object system. It depends on the object’s position relative to a chosen reference level—typically the ground or floor level. This reference point is arbitrary, but consistent use allows us to focus on changes in gravitational potential energy, which correspond directly to the work done.

(a) The weight attached to the cuckoo clock is raised by a height h shown by a displacement vector d pointing upward. The weight is attached to a winding chain labeled with a force F vector pointing downward. Vector d is also shown in the same direction as force F. E in is equal to W and W is equal to m g h. (b) The weight attached to the cuckoo clock moves downward. E out is equal to m g h. — Figure 43.1: The work done to lift the mass increases the gravitational potential energy of the system (a). As the mass moves downward (b), that potential energy is transformed into kinetic energy or transferred into mechanical motion such as powering a clock.

Converting Between Potential Energy and Kinetic Energy

If the object is allowed to fall, gravity accelerates it, transforming its gravitational potential energy into kinetic energy. The amount of energy converted is equal to $m g h$ . Thanks to the work-energy theorem, we know this corresponds exactly to the increase in kinetic energy as the object speeds up.

Let’s calculate a simple example. Suppose a 0.500-kg weight is lifted 1.00 m. The gravitational potential energy gained is:

${PE}_{g} = m g h = (0.500 kg) (9.80 {m/s}^{2}) (1.00 m) = 4.90 J .$

If the weight falls, that energy becomes 4.90 J of kinetic energy—no need to reanalyze the forces or acceleration.

Using Potential Energy to Simplify Calculations

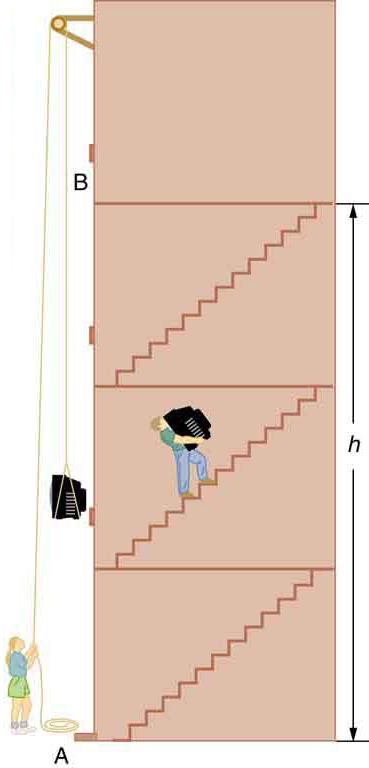
One major advantage of using potential energy is that it depends only on vertical displacement, not on the path taken. Whether you lift the object straight up, along a ramp, or over a curved staircase, the change in ${PE}_{g}$ is the same, as long as the vertical height change is the same. This concept is demonstrated in Figure 43.2, which shows different paths from point A to B. In all cases, the vertical height change is $h$ , so:

$Δ {PE}_{g} = m g h .$

This property makes gravity a conservative force—one for which the work done depends only on initial and final positions, not on the path taken. That’s why gravitational potential energy is such a useful concept in biology, health science, and engineering applications: it allows us to solve problems without tracking forces along every point of a complex path.

There is a four-story building. A person is carrying a television up the stairs of the building. The height of third story is h from the ground. A girl is standing outside the building and is lifting a similar television with the help of a pulley. — Figure 43.2: Regardless of the path taken, the change in gravitational potential energy ${PE}_{g} = m g h$ is the same, because it depends only on vertical height.

Example 43.1: The Force to Stop Falling

A 60.0-kg person jumps onto the floor from a height of 3.00 m. If he lands stiffly (with his knee joints compressing by 0.500 cm), calculate the force on the knee joints.

Strategy

This person’s energy is brought to zero in this situation by the work done on him by the floor as he stops. The initial ${PE}_{g}$ is transformed into $KE$ as he falls. The work done by the floor reduces this kinetic energy to zero.

Solution

The work done on the person by the floor as he stops is given by

W = Fd cos θ = - Fd,

with a minus sign because the displacement while stopping and the force from floor are in opposite directions $(cos θ = cos 180º = - 1)$ . The floor removes energy from the system, so it does negative work.

The kinetic energy the person has upon reaching the floor is the amount of potential energy lost by falling through height $h$ :

KE = - Δ {PE}_{g} = - mgh,

The distance $d$ that the person’s knees bend is much smaller than the height $h$ of the fall, so the additional change in gravitational potential energy during the knee bend is ignored.

The work $W$ done by the floor on the person stops the person and brings the person’s kinetic energy to zero:

W = - KE = mgh .

Combining this equation with the expression for $W$ gives

- Fd = mgh .

Recalling that $h$ is negative because the person fell down, the force on the knee joints is given by

F = - \frac{mgh}{d} = - \frac{(60.0 kg) (9.80 m {/s}^{2}) (- 3 . 00 m)}{5.00 \times 10^{- 3} m} = 3.53 \times 10^{5} N .

Discussion

Such a large force (500 times more than the person’s weight) over the short impact time is enough to break bones. A much better way to cushion the shock is by bending the legs or rolling on the ground, increasing the time over which the force acts. A bending motion of 0.5 m this way yields a force 100 times smaller than in the example. A kangaroo’s hopping shows this method in action. The kangaroo is the only large animal to use hopping for locomotion, but the shock in hopping is cushioned by the bending of its hind legs in each jump.(See Figure 43.3)

A hopping kangaroo is shown landing on the ground in one photograph and in the air just after taking another jump in the second photograph. — Figure 43.3: The work done by the ground upon the kangaroo reduces its kinetic energy to zero as it lands. However, by applying the force of the ground on the hind legs over a longer distance, the impact on the bones is reduced. (credit: Chris Samuel, Flickr)

Example 43.2: Finding the Speed of a Roller Coaster from its Height

(a) What is the final speed of the roller coaster shown in Figure 43.4 if it starts from rest at the top of the 20.0 m hill and work done by frictional forces is negligible? (b) What is its final speed (again assuming negligible friction) if its initial speed is 5.00 m/s?

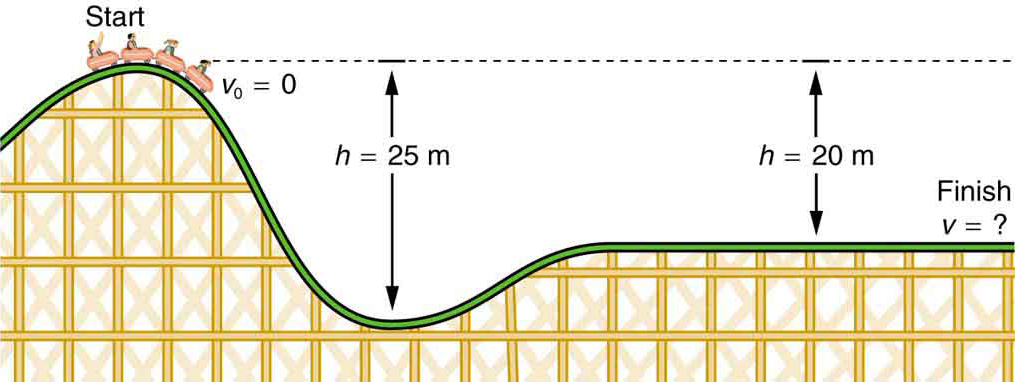
A roller coaster track is shown with a car about to go downhill. The initial height of the roller coaster car on the track is twenty-five meters from the lowest part of the track and its speed v sub zero is equal to zero. The roller coaster’s height from the level part of the track is twenty meters. The finish point of the car is on the level part of the track and the speed at that point is unknown. — Figure 43.4: The speed of a roller coaster increases as gravity pulls it downhill and is greatest at its lowest point. Viewed in terms of energy, the roller-coaster-Earth system’s gravitational potential energy is converted to kinetic energy. If work done by friction is negligible, all $Δ {PE}_{g}$ is converted to $KE$ .

Strategy

The roller coaster loses potential energy as it goes downhill. We neglect friction, so that the remaining force exerted by the track is the normal force, which is perpendicular to the direction of motion and does no work. The net work on the roller coaster is then done by gravity alone. The loss of gravitational potential energy from moving downward through a distance $h$ equals the gain in kinetic energy. This can be written in equation form as $- Δ {PE}_{g} = Δ KE$ . Using the equations for ${PE}_{g}$ and $KE$ , we can solve for the final speed $v$ , which is the desired quantity.

Solution for (a)

Here the initial kinetic energy is zero, so that $ΔKE = \frac{1}{2} {mv}^{2}$ . The equation for change in potential energy states that ${ΔPE}_{g} = mgh$ . Since $h$ is negative in this case, we will rewrite this as ${ΔPE}_{g} = - mg ∣ h ∣$ to show the minus sign clearly. Thus,

- Δ {PE}_{g} = Δ KE

becomes

mg ∣ h ∣= \frac{1}{2} {mv}^{2} .

Solving for $v$ , we find that mass cancels and that

v = \sqrt{2 g ∣ h ∣} .

Substituting known values,

\begin{array}{lll} v & = & \sqrt{2 (9 . 80 m {/s}^{2}) (20.0 m)} \\ = & 19 .8 m/s. \end{array}

Solution for (b)

Again $- {ΔPE}_{g} = ΔKE$ . In this case there is initial kinetic energy, so $ΔKE = \frac{1}{2} m v^{2} - \frac{1}{2} m {v_{0}}^{2}$ . Thus,

mg ∣ h ∣= \frac{1}{2} {mv}^{2} - \frac{1}{2} m {v_{0}}^{2} .

Rearranging gives

\frac{1}{2} {mv}^{2} = mg ∣ h ∣ + \frac{1}{2} m {v_{0}}^{2} .

This means that the final kinetic energy is the sum of the initial kinetic energy and the gravitational potential energy. Mass again cancels, and

v = \sqrt{2 g ∣ h ∣ + {v_{0}}^{2}} .

This equation is very similar to the kinematics equation $v = \sqrt{{v_{0}}^{2} + 2 ad}$ , but it is more general—the kinematics equation is valid only for constant acceleration, whereas our equation above is valid for any path regardless of whether the object moves with a constant acceleration. Now, substituting known values gives

\begin{array}{lll} v & = & \sqrt{2 (9.80 {m/s}^{2}) (20 .0 m) + {(5 .00 m/s)}^{2}} \\ = & 20.4 m/s. \end{array}

Discussion and Implications

First, note that mass cancels. This is quite consistent with observations made in Falling Objects that all objects fall at the same rate if friction is negligible. Second, only the speed of the roller coaster is considered; there is no information about its direction at any point. This reveals another general truth. When friction is negligible, the speed of a falling body depends only on its initial speed and height, and not on its mass or the path taken. For example, the roller coaster will have the same final speed whether it falls 20.0 m straight down or takes a more complicated path like the one in the figure. Third, and perhaps unexpectedly, the final speed in part (b) is greater than in part (a), but by far less than 5.00 m/s. Finally, note that speed can be found at any height along the way by simply using the appropriate value of $h$ at the point of interest.

We have seen that the work done by or against gravity depends solely on the initial and final positions of an object, and not on the path taken between those positions. This path independence allowed us to define the concept of gravitational potential energy, a powerful simplification in solving real-world problems.

Interestingly, gravity is not unique in this regard. Other forces also exhibit this path-independent behavior, and for such forces, we can define corresponding potential energies. This broader insight leads us naturally to a foundational concept in physics: the law of conservation of energy. By examining how energy transforms between different forms—such as from kinetic to potential or vice versa—we will develop a more complete understanding of how energy behaves in a wide variety of physical systems, from falling objects to biological motion and beyond.

Making Connections: Take-Home Investigation—Converting Potential to Kinetic Energy

You can explore the relationship between gravitational potential energy and kinetic energy using this simple at-home experiment.

Materials:

A marble
A ruler with a groove along its length (or a small ramp)
A hardcover book
A stopwatch
A measuring tape or meter stick

Instructions:

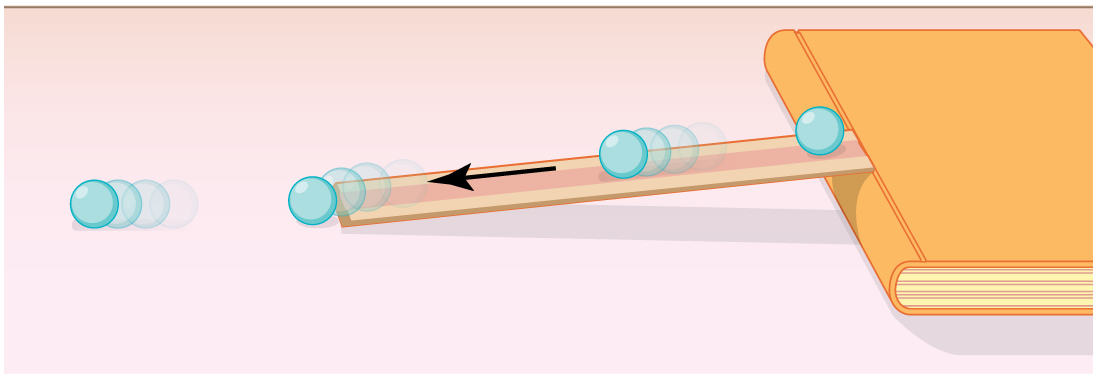
Create an incline by resting one end of the ruler on the book like the one illustrated in Figure 43.5.
Place the marble at the 10-cm mark on the ruler. Release the marble from rest and allow it to roll down the ramp.
When the marble reaches the flat surface, use a stopwatch to time how long it takes to travel a distance of 1 meter.
Repeat the measurement from the 20-cm and 30-cm release points.
For each case, calculate the speed using:

$v = \frac{1, m}{time}$
Then calculate:

$v^{2}$
Plot $v^{2}$ versus the vertical height of release.

Interpretation:
If the graph of $v^{2}$ versus height is a straight line, it confirms the proportionality between kinetic energy and gravitational potential energy:

$\frac{1}{2} m v^{2} \propto m g h$

This relationship demonstrates the conservation of mechanical energy: gravitational potential energy is transformed into kinetic energy as the marble descends.

A book is lying on the table and one end of a ruler rests on the edge of this book while the other end rests on the table, making it an incline. A marble is shown rolling down the ruler. — Figure 43.5: A marble rolls down a ruler, and its speed on the level surface is measured.

Section Summary

Work done against gravity in lifting an object becomes potential energy stored in the object–Earth system.
The change in gravitational potential energy is given by:

$Δ {PE}_{g} = m g h$

where:
- $m$ is mass,
- $g$ is the acceleration due to gravity,
- $h$ is the change in vertical height.
Gravitational potential energy is relative—only differences in energy matter:

$Δ {PE}_{g}$
As an object descends without friction, gravitational potential energy is converted into kinetic energy:

$Δ KE = - Δ {PE}_{g}$
This illustrates a special case of the conservation of mechanical energy:

$\frac{1}{2} m v^{2} + m g h = constant$

Conceptual Questions

In Example 43.2, we calculated the final speed of a roller coaster that descended 20 m in height and had an initial speed of 5 m/s downhill. Suppose the roller coaster had had an initial speed of 5 m/s uphill instead, and it coasted uphill, stopped, and then rolled back down to a final point 20 m below the start. We would find in that case that it had the same final speed. Explain in terms of conservation of energy.
Does the work you do on a book when you lift it onto a shelf depend on the path taken? On the time taken? On the height of the shelf? On the mass of the book?

Problems & Exercises

A hydroelectric power facility (see Figure 43.6) converts the gravitational potential energy of water behind a dam to electric energy. (a) What is the gravitational potential energy relative to the generators of a lake of volume $50.0 k m^{3}$ ( $mass = 5.00 \times 10^{13} kg)$ , given that the lake has an average height of 40.0 m above the generators? (b) Compare this with the energy stored in a 9-megaton fusion bomb.

Figure 43.6: Hydroelectric facility (credit: Denis Belevich, Wikimedia Commons)
(a) How much gravitational potential energy (relative to the ground on which it is built) is stored in the Great Pyramid of Cheops, given that its mass is about $7 \times 10^{9} kg$ and its center of mass is 36.5 m above the surrounding ground? (b) How does this energy compare with the daily food intake of a person?
Suppose a 350-g kookaburra (a large kingfisher bird) picks up a 75-g snake and raises it 2.5 m from the ground to a branch. (a) How much work did the bird do on the snake? (b) How much work did it do to raise its own center of mass to the branch?
In Example 43.2 we found that the speed of a roller coaster that had descended 20.0 m was only slightly greater when it had an initial speed of 5.00 m/s than when it started from rest. This implies that $Δ {PE >> KE}_{i}$ . Confirm this statement by taking the ratio of $Δ PE$ to ${KE}_{i}$ . (Note that mass cancels.)
A 100-g toy car is propelled by a compressed spring that starts it moving. The car follows the curved track in Figure 43.7. Show that the final speed of the toy car is 0.687 m/s if its initial speed is 2.00 m/s and it coasts up the frictionless slope, gaining 0.180 m in altitude.

Figure 43.7: A toy car moves up a sloped track. (credit: Leszek Leszczynski, Flickr)
In a downhill ski race, surprisingly, little advantage is gained by getting a running start. (This is because the initial kinetic energy is small compared with the gain in gravitational potential energy on even small hills.) To demonstrate this, find the final speed and the time taken for a skier who skies 70.0 m along a $30º$ slope neglecting friction: (a) Starting from rest. (b) Starting with an initial speed of 2.50 m/s. (c) Does the answer surprise you? Discuss why it is still advantageous to get a running start in very competitive events.

Glossary

gravitational potential energy: the energy an object has due to its position in a gravitational field

License

Icon for the Creative Commons Attribution 4.0 International License

Work Done Against Gravity

Converting Between Potential Energy and Kinetic Energy

Using Potential Energy to Simplify Calculations

Example 43.1: The Force to Stop Falling

Strategy

Solution

Discussion

Example 43.2: Finding the Speed of a Roller Coaster from its Height

Strategy

Solution for (a)

Solution for (b)

Discussion and Implications

Making Connections: Take-Home Investigation—Converting Potential to Kinetic Energy

Section Summary

Conceptual Questions

Problems & Exercises

Glossary

License

Share This Book