In many healthcare and biological settings, measuring pressure is essential. From checking blood pressure to inflating medical devices, understanding how we measure and interpret pressure is key. For example, when you arrive at a gas station with a flat tire, the pressure gauge might read zero. But why? Even though the atmosphere pushes on the tire, the gauge shows no pressure. This is because most pressure gauges are calibrated to read zero at atmospheric pressure.

The same concept applies to medical pressure readings. Blood pressure gauges do not measure the total (absolute) pressure in your arteries, but rather how much greater that pressure is than atmospheric pressure. This difference is what we call gauge pressure.

In biological systems, atmospheric pressure contributes to the total pressure in fluids unless they are enclosed in rigid structures. Based on Pascal’s Principle, pressure applied to an enclosed fluid is transmitted equally in all directions. Thus, the total or absolute pressure is given by:

Here, [latex]{P}_{\text{abs}}[/latex] is absolute pressure, [latex]{P}_{\text{g}}[/latex] is gauge pressure, and [latex]{P}_{\text{atm}}[/latex] is atmospheric pressure. For example, if a tire gauge reads 34 psi, the actual pressure inside the tire is:

Fluids can only push; they cannot pull. This means the lowest possible absolute pressure is zero, which corresponds to a vacuum. Therefore, the lowest gauge pressure is:

This value gives an absolute pressure of zero, the physical limit for fluids. There is no limit to how high gauge pressure can be.

Measuring Pressure in Practice

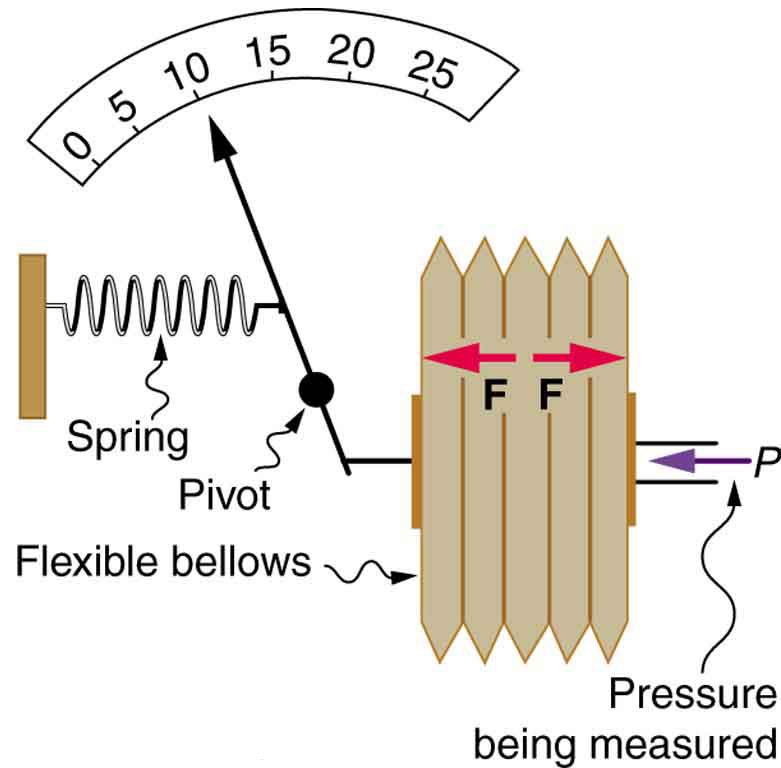
Pascal’s Principle allows pressure to be transmitted through fluids without loss. This property is exploited in pressure measurement tools such as tire gauges, blood pressure cuffs, and medical devices. These tools translate pressure into mechanical motion or electronic signals to give a reading. Figure 80.1 shows one of the many types of mechanical pressure gauges in use today. In all mechanical pressure gauges, pressure results in a force that is converted (or transduced) into some type of readout.

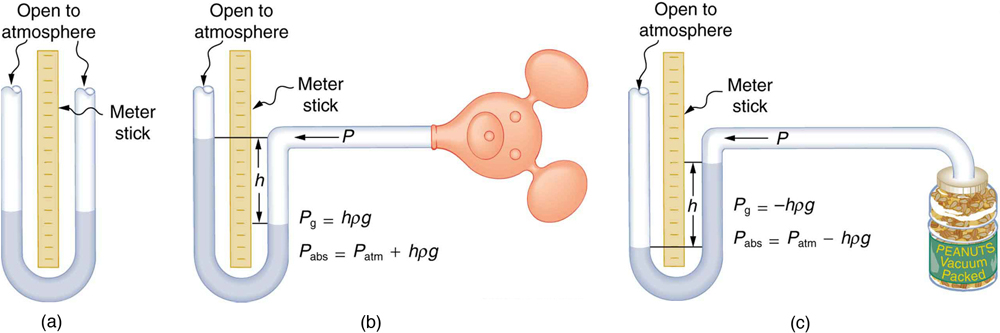
Another common pressure measuring device is the open-tube manometer like the one shown in Figure 80.2, which uses the height difference in a fluid column to determine pressure based on the equation:

Here, [latex]h[/latex] is the height difference of the fluid, [latex]\rho[/latex] is the fluid’s density, and [latex]g[/latex] is the acceleration due to gravity.

Blood Pressure and Mercury Manometers

Mercury manometers are commonly used in clinical settings to measure arterial blood pressure. An inflatable cuff is wrapped around the upper arm at heart level as shown in Figure 80.3. Pressure is applied through the cuff and is transmitted through the arm’s arteries and to the mercury column. When cuff pressure exceeds blood pressure, arterial flow stops. As cuff pressure is slowly released, blood flow resumes, allowing measurement of both systolic and diastolic pressures.

Normal blood pressure is around 120/80 mm Hg. Because mercury is 13.6 times denser than water, it allows compact and precise pressure measurement. Converting mm Hg to Pascals:

A barometer is a device that measures atmospheric pressure. A mercury barometer is shown in Figure 80.4. This device measures atmospheric pressure, rather than gauge pressure, because there is a nearly pure vacuum above the mercury in the tube. The height of the mercury is such that [latex]\mathrm{h\rho g}={P}_{\text{atm}}[/latex]. When atmospheric pressure varies, the mercury rises or falls, giving important clues to weather forecasters. The barometer can also be used as an altimeter, since average atmospheric pressure varies with altitude. Mercury barometers and manometers are so common that units of mm Hg are often quoted for atmospheric pressure and blood pressures. Table 80.1 gives conversion factors for some of the more commonly used units of pressure.