"

Dynamics: Force and Newton’s Laws of Motion and Applications: Friction, Drag and Elasticity

30 Friction

Learning Objectives

  • Discuss the general characteristics of friction.
  • Describe the various types of friction.
  • Calculate the magnitude of static and kinetic friction.

Friction

Friction is a force that opposes relative motion between two surfaces in contact. It allows humans and animals to walk, grasp, and manipulate objects effectively, yet it also resists motion when trying to move heavy loads. Despite its importance, friction remains a complex force that we primarily understand through experimentation and observation.

Friction acts parallel to the surface of contact and always in the direction that opposes the relative motion or the attempt to move. It is categorized into two main types:

  • Static friction: Acts when there is no relative motion.
  • Kinetic friction: Acts when objects are sliding past each other.

Static vs. Kinetic Friction

Static Friction prevents motion. It adjusts up to a maximum value depending on the applied force. You can feel this when trying to push a heavy hospital bed or a patient lift—it resists motion until enough force is applied.

Kinetic Friction acts once motion begins. It is generally smaller than static friction, which is why it’s easier to keep an object moving than to start its motion.

Real-World Example: Moving a Patient Bed

When attempting to push a stationary patient bed:

  • You first encounter static friction.
  • Once the bed begins to roll, you experience kinetic friction, which is less than the force required to initially move it.

Frictional force is also affected by the normal force, which increases with the weight of the object. For example, placing more equipment on a gurney increases the normal force and therefore the friction.

Microscopic View of Friction

Even surfaces that appear smooth are rough at the microscopic level like in Figure 30.1. The peaks and valleys at the interface cause resistance. Adhesion between molecules adds further resistance, which is dependent on the nature of the materials in contact.

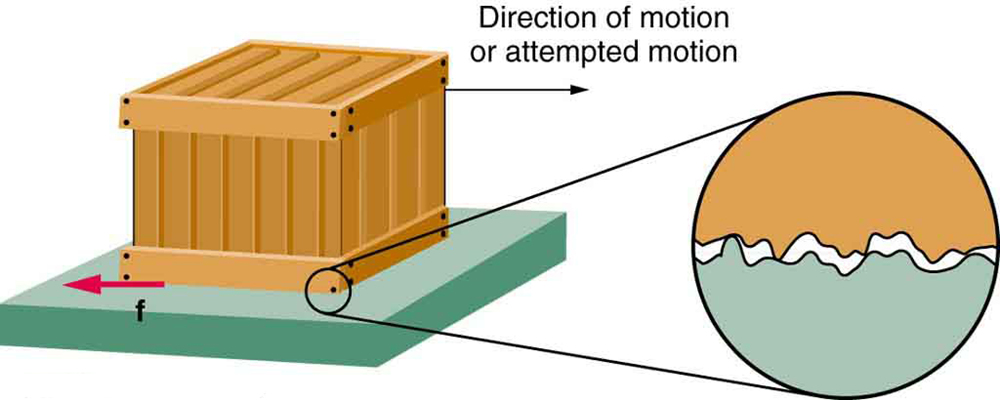
The figure shows a crate on a flat surface, and a magnified view of a bottom corner of the crate and the supporting surface. The magnified view shows that there is roughness in the two surfaces in contact with each other. A black arrow points toward the right, away from the crate, and it is labeled as the direction of motion or attempted motion. A red arrow pointing toward the left is located near the bottom left corner of the crate, at the interface between that corner and the supporting surface. The red arrow is labeled as f, representing friction between the two surfaces in contact with each other.
Figure 30.1: Frictional forces, such as [latex]f[/latex], oppose motion due to microscopic roughness and molecular adhesion. As the object attempts to slide, it must climb over surface irregularities or break adhesive bonds. Smoother materials or lubricated surfaces reduce these effects.

Equations for Friction

Static Friction:

[latex]f_{s} \leq \mu_{s} N[/latex]

  • [latex]\mu_s[/latex] = coefficient of static friction
  • [latex]N[/latex] = normal force

Maximum static friction: [latex]f_{s,(\text{max})} = \mu_s N[/latex]

Kinetic Friction:

[latex]f_k = \mu_k N[/latex]

  • [latex]\mu_k[/latex] = coefficient of kinetic friction

As seen in Table 30.1, the coefficients of kinetic friction are less than their static counterparts. That values of [latex]\mu[/latex] in Table 30.1 are stated to only one or, at most, two digits is an indication of the approximate description of friction given by the above two equations.

Table 30.1: Coefficients of Static and Kinetic Friction
System Static friction[latex]{\mu }_{\text{s}}[/latex] Kinetic friction[latex]{\mu }_{\text{k}}[/latex]
Rubber on dry concrete 1.0 0.7
Rubber on wet concrete 0.7 0.5
Wood on wood 0.5 0.3
Waxed wood on wet snow 0.14 0.1
Metal on wood 0.5 0.3
Steel on steel (dry) 0.6 0.3
Steel on steel (oiled) 0.05 0.03
Teflon on steel 0.04 0.04
Bone lubricated by synovial fluid 0.016 0.015
Shoes on wood 0.9 0.7
Shoes on ice 0.1 0.05
Ice on ice 0.1 0.03
Steel on ice 0.4 0.02

These coefficients show how friction varies with materials and surface conditions. For instance, synovial fluid in joints allows for extremely low friction, enabling smooth motion between bones.

Worked Example: Hospital Gurney

A gurney has a mass of 100 kg. What force is required to:

  1. Start moving it across a hospital floor (static friction [latex]\mu_s = 0.45[/latex])?
  2. Keep it moving at constant speed (kinetic friction [latex]\mu_k = 0.30[/latex])?

Solution:

  • Weight: [latex]W = mg = 100 \text{ kg} \times 9.8 \text{ m/s}^2 = 980 \text{ N}[/latex]
  • Max static friction: [latex]f_{s,(\text{max})} = 0.45 \times 980 = 441 \text{ N}[/latex]
  • Kinetic friction: [latex]f_k = 0.30 \times 980 = 294 \text{ N}[/latex]

Thus, a minimum of 441 N is required to start motion, and 294 N to maintain motion.

Friction in Biology and Medicine

  • Joints: Cartilage and synovial fluid reduce friction to levels even lower than ice.
  • Arthritis: Increased joint friction from damaged cartilage impairs movement.
  • Artificial Joints: Made of materials with low [latex]\mu[/latex], like titanium and polyethylene.
  • Ultrasound Gel: Reduces skin friction for smooth probe movement.
  • Saliva & Mucus: Act as natural lubricants for swallowing and organ motion

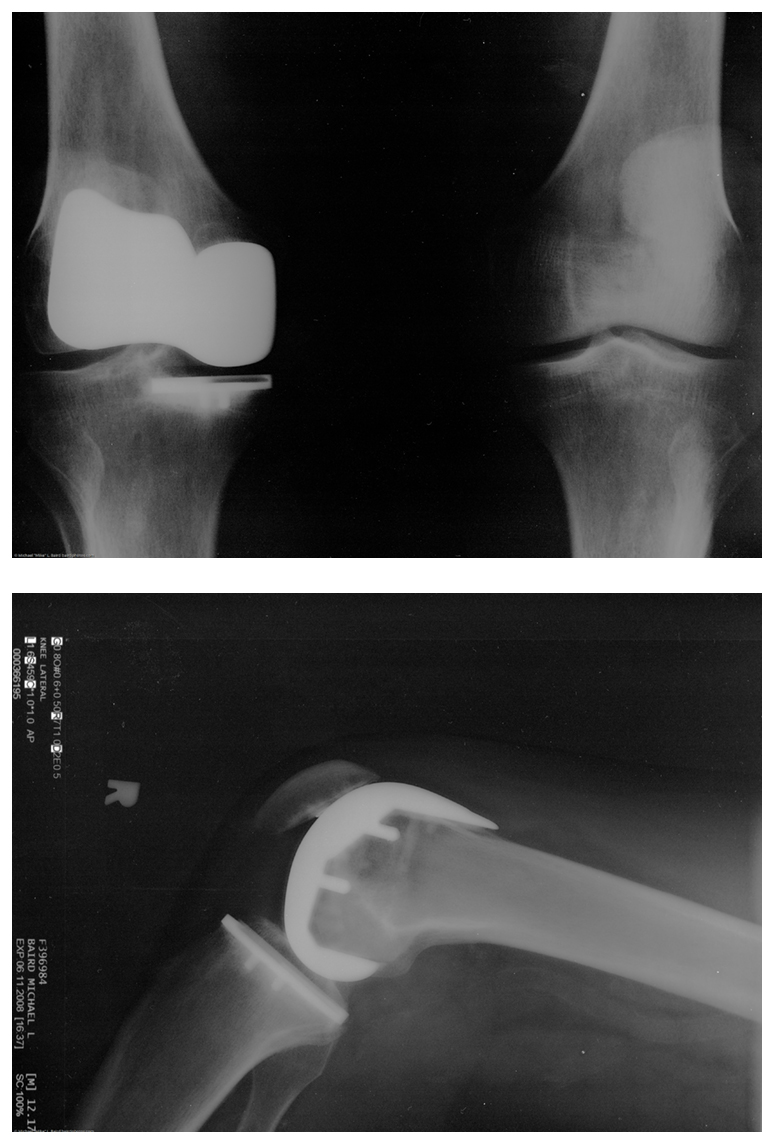
Figure 30.2 shows an X-ray of a post-operative artificial knee. These implants are engineered for ultra-low friction to mimic the smooth gliding action of a natural joint. This principle mirrors the function of biological joints, as discussed earlier in the section on synovial fluid and cartilage.

Take-Home Experiment

Find a small plastic object (such as a food container) and slide it on a kitchen table by giving it a gentle tap. Now spray water on the table, simulating a light shower of rain. What happens now when you give the object the same-sized tap? Now add a few drops of (vegetable or olive) oil on the surface of the water and give the same tap. What happens now? This latter situation is particularly important for drivers to note, especially after a light rain shower. Why?

Many people have experienced the slipperiness of walking on ice. However, many parts of the body, especially the joints, have much smaller coefficients of friction—often three or four times less than ice. A joint is formed by the ends of two bones, which are connected by thick tissues. The knee joint is formed by the lower leg bone (the tibia) and the thighbone (the femur). The hip is a ball (at the end of the femur) and socket (part of the pelvis) joint. The ends of the bones in the joint are covered by cartilage, which provides a smooth, almost glassy surface. The joints also produce a fluid (synovial fluid) that reduces friction and wear. A damaged or arthritic joint can be replaced by an artificial joint (Figure 30.2). These replacements can be made of metals (stainless steel or titanium) or plastic (polyethylene), also with very small coefficients of friction.

Two X-x rays of an artificial knee replacement are shown.
Figure 30.2: Artificial knee replacement is a procedure that has been performed for more than 20 years. In this figure, we see the post-op x rays of the right knee joint replacement. (credit: Mike Baird, Flickr)

Other natural lubricants include saliva produced in our mouths to aid in the swallowing process, and the slippery mucus found between organs in the body, allowing them to move freely past each other during heartbeats, during breathing, and when a person moves. Artificial lubricants are also common in hospitals and doctor’s clinics. For example, when ultrasonic imaging is carried out, the gel that couples the transducer to the skin also serves to to lubricate the surface between the transducer and the skin—thereby reducing the coefficient of friction between the two surfaces. This allows the transducer to mover freely over the skin.

Example 30.1: Skiing Exercise

A skier with a mass of 62 kg is sliding down a snowy slope. Find the coefficient of kinetic friction for the skier if friction is known to be 45.0 N.

Strategy

The magnitude of kinetic friction was given in to be 45.0 N. Kinetic friction is related to the normal force
[latex]N[/latex] as [latex]{f}_{\text{k}}={\mu }_{\text{k}}N[/latex]; thus, the coefficient of kinetic friction can be found if we can find the normal force of the skier on a slope. The normal force is always perpendicular to the surface, and since there is no motion perpendicular to the surface, the normal force should equal the component of the skier’s weight perpendicular to the slope. (See the skier and free-body diagram in Figure 30.3.)

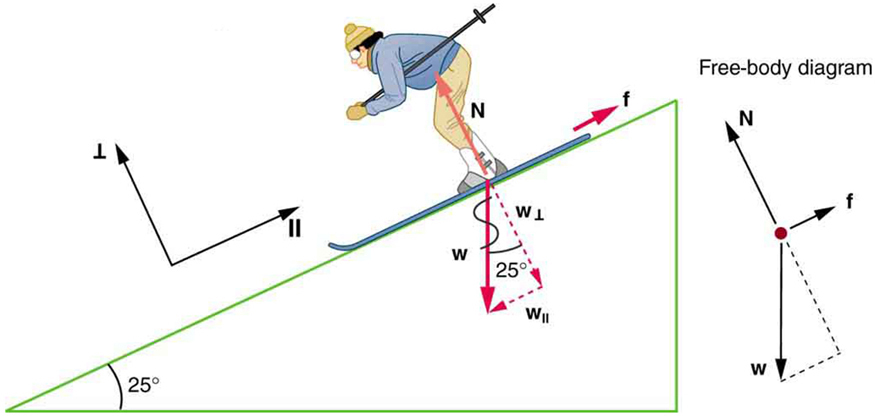
The figure shows a skier going down a slope that forms an angle of 25 degrees with the horizontal. The weight of the skier, labeled w, is represented by a red arrow pointing vertically downward. This weight is divided into two components, w perpendicular is perpendicular to the slope, and w parallel is parallel to the slope. The normal force, labeled N, is also perpendicular to the slope, equal in magnitude but opposite in direction to w perpendicular. The friction, f, is represented by a red arrow pointing upslope. In addition, the figure shows a free body diagram that shows the relative magnitudes and directions of w, f, and N.
Figure 30.3: The motion of the skier and friction are parallel to the slope and so it is most convenient to project all forces onto a coordinate system where one axis is parallel to the slope and the other is perpendicular (axes shown to left of skier). [latex]\mathbf{\text{N}}[/latex] (the normal force) is perpendicular to the slope, and [latex]\mathbf{\text{f}}[/latex] (the friction) is parallel to the slope, but [latex]\mathbf{\text{w}}[/latex] (the skier’s weight) has components along both axes, namely [latex]{\mathbf{\text{w}}}_{\text{⊥}}[/latex] and [latex]{\mathbf{\text{W}}}_{//}[/latex]. [latex]\mathbf{N}[/latex] is equal in magnitude to [latex]{\mathbf{w}}_{\perp }[/latex], so there is no motion perpendicular to the slope. However, [latex]\mathbf{f}[/latex] is less than [latex]{\mathbf{W}}_{\text{//}}[/latex] in magnitude, so there is acceleration down the slope (along the x-axis).

That is,

[latex]N={w}_{\perp }=w\phantom{\rule{0.25em}{0ex}}\text{cos}\phantom{\rule{0.15em}{0ex}}\text{25º}=\text{mg}\phantom{\rule{0.25em}{0ex}}\text{cos}\phantom{\rule{0.15em}{0ex}}\text{25º}.[/latex]

Substituting this into our expression for kinetic friction, we get

[latex]{f}_{\text{k}}={\mu }_{\text{k}}\text{mg}\phantom{\rule{0.25em}{0ex}}\text{cos}\phantom{\rule{0.15em}{0ex}}\text{25º},[/latex]

which can now be solved for the coefficient of kinetic friction [latex]{\mu }_{\text{k}}[/latex].

Solution

Solving for [latex]{\mu }_{k}[/latex] gives

[latex]{\mu }_{\text{k}}=\frac{{f}_{\text{k}}}{N}=\frac{{f}_{\text{k}}}{w\phantom{\rule{0.15em}{0ex}}\text{cos}\phantom{\rule{0.15em}{0ex}}\text{25º}}=\frac{{f}_{\text{k}}}{\text{mg}\phantom{\rule{0.15em}{0ex}}\text{cos}\phantom{\rule{0.15em}{0ex}}\text{25º}.}[/latex]

Substituting known values on the right-hand side of the equation,

[latex]{\mu }_{\text{k}}=\frac{\text{45.0 N}}{\left(\text{62 kg}\right)\left(9\text{.}\text{80 m}{\text{/s}}^{2}\right)\left(0\text{.}\text{906}\right)}=0\text{.}\text{082}.[/latex]

Discussion

This result is a little smaller than the coefficient listed in Table 30.1 for waxed wood on snow, but it is still reasonable since values of the coefficients of friction can vary greatly. In situations like this, where an object of mass [latex]m[/latex] slides down a slope that makes an angle [latex]\theta[/latex]
with the horizontal, friction is given by [latex]{f}_{\text{k}}={\mu }_{\text{k}}\text{mg}\phantom{\rule{0.15em}{0ex}}\text{cos}\phantom{\rule{0.15em}{0ex}}\theta[/latex]. All objects will slide down a slope with constant acceleration under these circumstances. Proof of this is left for this chapter’s Problems and Exercises.

Take-Home Experiment

An object will slide down an inclined plane at a constant velocity if the net force on the object is zero. We can use this fact to measure the coefficient of kinetic friction between two objects. As shown in Example 30.1, the kinetic friction on a slope [latex]{f}_{\text{k}}={\mu }_{\text{k}}\text{mg}\phantom{\rule{0.25em}{0ex}}\text{cos}\phantom{\rule{0.15em}{0ex}}\theta[/latex]. The component of the weight down the slope is equal to [latex]\text{mg}\phantom{\rule{0.25em}{0ex}}\text{sin}\phantom{\rule{0.15em}{0ex}}\theta[/latex] (see the free-body diagram in Figure 30.3). These forces act in opposite directions, so when they have equal magnitude, the acceleration is zero. Writing these out:

[latex]{f}_{\text{k}}={\text{Fg}}_{\text{x}}[/latex]
[latex]{\mu }_{\text{k}}\text{mg}\phantom{\rule{0.25em}{0ex}}\text{cos}\phantom{\rule{0.25em}{0ex}}\theta =\text{mg}\phantom{\rule{0.25em}{0ex}}\text{sin}\phantom{\rule{0.25em}{0ex}}\theta .[/latex]

Solving for [latex]{\mu }_{\text{k}}[/latex], we find that

[latex]{\mu }_{\text{k}}=\frac{\text{mg}\phantom{\rule{0.25em}{0ex}}\text{sin}\phantom{\rule{0.25em}{0ex}}\theta }{\text{mg}\phantom{\rule{0.25em}{0ex}}\text{cos}\phantom{\rule{0.25em}{0ex}}\theta }=\text{tan}\phantom{\rule{0.25em}{0ex}}\theta .[/latex]

Put a coin on a book and tilt it until the coin slides at a constant velocity down the book. You might need to tap the book lightly to get the coin to move. Measure the angle of tilt relative to the horizontal and find [latex]{\mu }_{\text{k}}[/latex]. Note that the coin will not start to slide at all until an angle greater than [latex]\theta[/latex] is attained, since the coefficient of static friction is larger than the coefficient of kinetic friction. Discuss how this may affect the value for [latex]{\mu }_{\text{k}}[/latex] and its uncertainty.

We have discussed that when an object rests on a horizontal surface, there is a normal force supporting it equal in magnitude to its weight. Furthermore, simple friction is always proportional to the normal force.

Making Connections: Submicroscopic Explanations of Friction

Until now, we’ve described friction based on what we observe at the macroscopic level—the everyday resistance we feel when dragging a hospital bed or sliding a foot across a floor. But friction originates at the atomic and molecular level, and recent advances in nanotechnology and surface science are helping explain its underlying mechanisms.

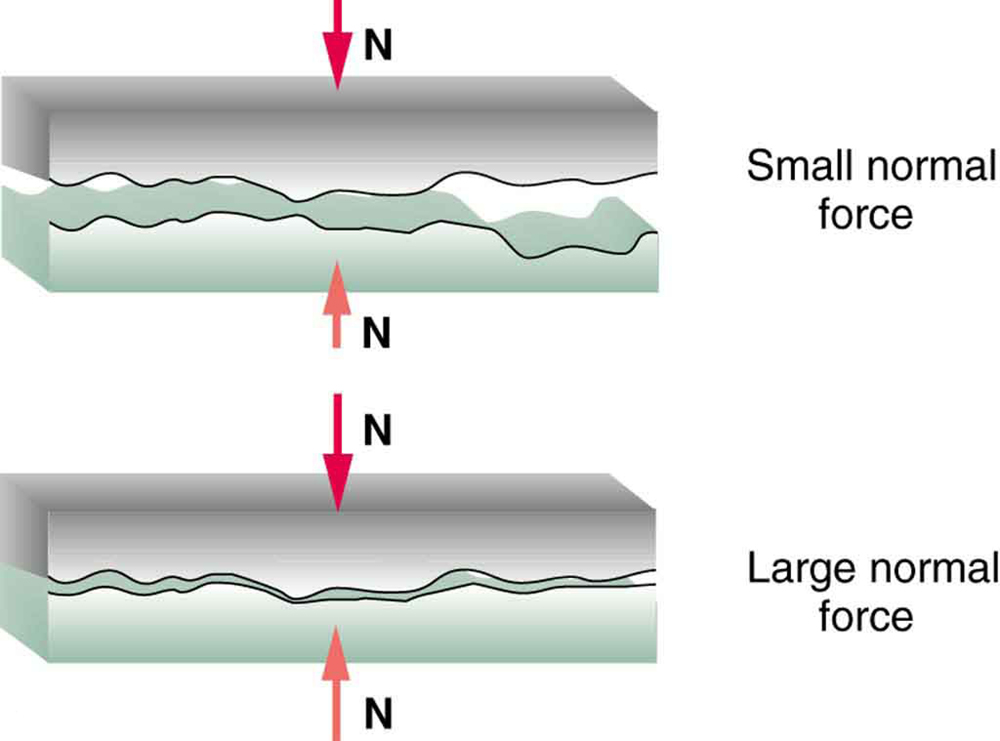
Why Isn’t Friction Proportional to Contact Area?

One puzzling feature of friction is that it is proportional to the normal force but not to the contact area. This seems counterintuitive—shouldn’t a larger contact area create more friction? However, microscopic studies reveal that only the highest points (asperities) of rough surfaces actually touch. The true contact area is a small fraction of the apparent area. When the normal force increases—say, by placing equipment on a gurney—it causes more of these high points to press into contact, which increases friction. This relationship is illustrated in Figure 30.4 

This figure has two parts, each of which shows two rough surfaces in close proximity to each other. In the first part, the normal force is small, so that the area of contact between the two surfaces is much smaller than their total area. In the second part, the normal force is large, so that the area of contact between the two surfaces has increased. As a result, the friction between the two surfaces in the second part is also greater than the friction in the first part.
Figure 30.4: Two rough surfaces in contact have a much smaller area of actual contact than their total area. When there is a greater normal force as a result of a greater applied force, the area of actual contact increases as does friction.

From Vibrations to Heat: Atomic Lattices in Motion

When two surfaces slide against one another—such as in a joint or between medical devices and skin—surface atoms stick momentarily and then break apart, causing vibrations in atomic lattices. These vibrations behave like sound waves that lose energy as they travel, converting that energy into heat. This helps explain why friction produces warmth.

This process is particularly relevant in prosthetic joint design, where controlling frictional heat can improve comfort and reduce tissue damage.

Atomic Deformation and Shear Stress

In laboratory settings, researchers use microscopic probes to drag across material surfaces and measure resistance forces. As shown in Figure 30.5, these probes deform slightly due to atomic-scale shear stress. The amount of force needed to overcome this resistance varies enormously across different materials—sometimes by a factor of [latex]10^{12}[/latex]! These findings help refine biomaterials used in implants and coatings, aiming to create ultra-low-friction surfaces in the body.

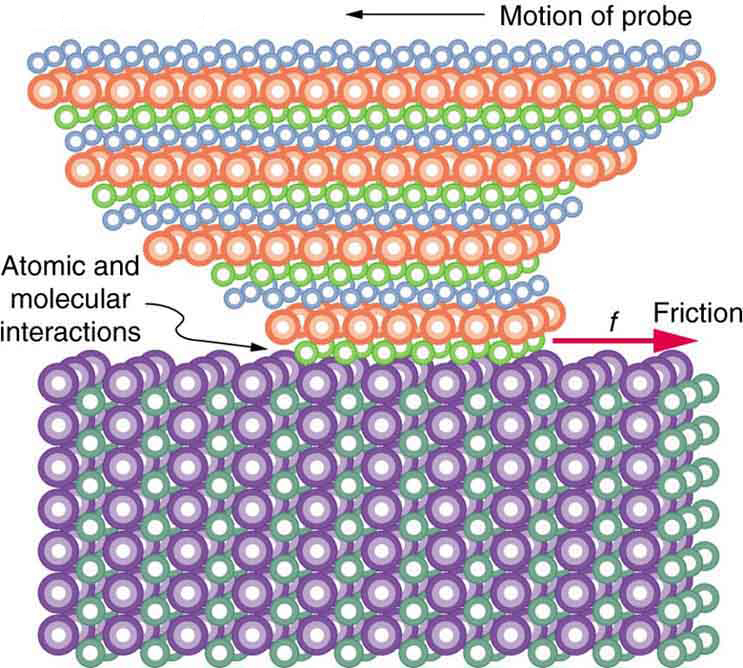
This figure shows a molecular model of a probe that is dragged over the surface of a substrate. The substrate is represented by a rectangular prism, made up of a grid of small spheres, each sphere representing an atom. The probe, made up of a different grid of small spheres, is in the form of an inverted pyramid with a flattened peak. The pyramid is somewhat distorted because of friction.
Figure 30.5: The tip of a probe is deformed sideways by frictional force as the probe is dragged across a surface. Measurements of how the force varies for different materials are yielding fundamental insights into the atomic nature of friction.

These microscopic insights allow us to develop better medical devices, artificial joints, and diagnostic tools—all optimized to minimize friction where needed or enhance grip where necessary. Advances in this field may eventually lead to nearly frictionless biomedical surfaces, saving energy and reducing wear in everything from robotic surgical tools to wheelchairs.

PhET Explorations: Forces and Motion

Explore the forces at work when you try to push a filing cabinet. Create an applied force and see the resulting friction force and total force acting on the cabinet. Charts show the forces, position, velocity, and acceleration vs. time. Draw a free-body diagram of all the forces (including gravitational and normal forces).

Figure 30.6: Forces and Motion

Section Summary

  • Friction is a contact force between systems that opposes the motion or attempted motion between them. Simple friction is proportional to the normal force [latex]N[/latex] pushing the systems together. (A normal force is always perpendicular to the contact surface between systems.) Friction depends on both of the materials involved. The magnitude of static friction[latex]{f}_{\text{s}}[/latex] between systems stationary relative to one another is given by
    [latex]{f}_{\text{s}}\le {\mu }_{\text{s}}N,[/latex]

    where [latex]{\mu }_{\text{s}}[/latex] is the coefficient of static friction, which depends on both of the materials.

  • The kinetic friction force [latex]{f}_{\text{k}}[/latex] between systems moving relative to one another is given by
    [latex]{f}_{\text{k}}={\mu }_{\text{k}}N,[/latex]

    where [latex]{\mu }_{\text{k}}[/latex] is the coefficient of kinetic friction, which also depends on both materials.

Conceptual Questions

  1. Define normal force. What is its relationship to friction when friction behaves simply?
  2. The glue on a piece of tape can exert forces. Can these forces be a type of simple friction? Explain, considering especially that tape can stick to vertical walls and even to ceilings.
  3. When you learn to drive, you discover that you need to let up slightly on the brake pedal as you come to a stop or the car will stop with a jerk. Explain this in terms of the relationship between static and kinetic friction.
  4. When you push a piece of chalk across a chalkboard, it sometimes screeches because it rapidly alternates between slipping and sticking to the board. Describe this process in more detail, in particular explaining how it is related to the fact that kinetic friction is less than static friction. (The same slip-grab process occurs when tires screech on pavement.)

Problems & Exercises

  1. A physics major is cooking breakfast when he notices that the frictional force between his steel spatula and his Teflon frying pan is only 0.200 N. Knowing the coefficient of kinetic friction between the two materials, he quickly calculates the normal force. What is it?
  2. (a) When rebuilding her car’s engine, a physics major must exert 300 N of force to insert a dry steel piston into a steel cylinder. What is the magnitude of the normal force between the piston and cylinder? (b) What is the magnitude of the force would she have to exert if the steel parts were oiled?
  3. (a) What is the maximum frictional force in the knee joint of a person who supports 66.0 kg of her mass on that knee? (b) During strenuous exercise it is possible to exert forces to the joints that are easily ten times greater than the weight being supported. What is the maximum force of friction under such conditions? The frictional forces in joints are relatively small in all circumstances except when the joints deteriorate, such as from injury or arthritis. Increased frictional forces can cause further damage and pain
  4. Suppose you have a 120-kg wooden crate resting on a wood floor. (a) What maximum force can you exert horizontally on the crate without moving it? (b) If you continue to exert this force once the crate starts to slip, what will the magnitude of its acceleration then be?
  5. (a) If half of the weight of a small [latex]1\text{.}\text{00}×{\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}\text{kg}\phantom{\rule{0.25em}{0ex}}[/latex]utility truck is supported by its two drive wheels, what is the magnitude of the maximum acceleration it can achieve on dry concrete? (b) Will a metal cabinet lying on the wooden bed of the truck slip if it accelerates at this rate? (c) Solve both problems assuming the truck has four-wheel drive.
  6. A team of eight dogs pulls a sled with waxed wood runners on wet snow (mush!). The dogs have average masses of 19.0 kg, and the loaded sled with its rider has a mass of 210 kg. (a) Calculate the magnitude of the acceleration starting from rest if each dog exerts an average force of 185 N backward on the snow. (b) What is the magnitude of the acceleration once the sled starts to move? (c) For both situations, calculate the magnitude of the force in the coupling between the dogs and the sled.
  7. Consider the 65.0-kg ice skater being pushed by two others shown in Figure 30.7. (a) Find the direction and magnitude of [latex]{\mathbf{F}}_{\text{tot}}[/latex], the total force exerted on her by the others, given that the magnitudes [latex]{F}_{1}[/latex] and [latex]{F}_{2}[/latex] are 26.4 N and 18.6 N, respectively. (b) What is her initial acceleration if she is initially stationary and wearing steel-bladed skates that point in the direction of [latex]{\mathbf{F}}_{\text{tot}}[/latex]? (c) What is her acceleration assuming she is already moving in the direction of [latex]{\mathbf{F}}_{\text{tot}}[/latex]? (Remember that friction always acts in the direction opposite that of motion or attempted motion between surfaces in contact.)
    (a) Overhead view of two ice skaters pushing on a third. One skater pushes with a force F two, represented by an arrow pointing up, and a second skater pushes with a force F one, represented by an arrow pointing from left to right. Vector F one and vector F two are along the arms of the two skaters acting on the third skater. A vector diagram is shown in the form of a right triangle in which the base is vector F one pointing east, and perpendicular to F one is vector F two pointing north. The resultant vector is shown by the hypotenuse pointing northeast. (b) Free-body diagram showing only the forces acting on the skater.
    Figure 30.7

  8. Show that the acceleration of any object down a frictionless incline that makes an angle [latex]\theta[/latex] with the horizontal is [latex]a=g\phantom{\rule{0.25em}{0ex}}\text{sin}\phantom{\rule{0.25em}{0ex}}\theta[/latex]. (Note that this acceleration is independent of mass.)
  9. Show that the acceleration of any object down an incline where friction behaves simply (that is, where [latex]{f}_{\text{k}}={\mu }_{\text{k}}N[/latex]) is [latex]a=g\left(\phantom{\rule{0.25em}{0ex}}\text{sin}\phantom{\rule{0.25em}{0ex}}\theta -{\mu }_{\text{k}}\text{cos}\phantom{\rule{0.25em}{0ex}}\theta \right).[/latex] Note that the acceleration is independent of mass and reduces to the expression found in the previous problem when friction becomes negligibly small [latex]\left({\mu }_{\text{k}}=0\right).[/latex]
  10. Calculate the deceleration of a snow boarder going up a [latex]5.0º[/latex], slope assuming the coefficient of friction for waxed wood on wet snow. The result of Exercise 9 may be useful, but be careful to consider the fact that the snow boarder is going uphill. Explicitly show how you follow the steps in Problem-Solving Strategies.
  11. (a) Calculate the acceleration of a skier heading down a [latex]\text{10}\text{.}0º[/latex] slope, assuming the coefficient of friction for waxed wood on wet snow. (b) Find the angle of the slope down which this skier could coast at a constant velocity. You can neglect air resistance in both parts, and you will find the result of Exercise 9 to be useful. Explicitly show how you follow the steps in the Problem-Solving Strategies.
  12. If an object is to rest on an incline without slipping, then friction must equal the component of the weight of the object parallel to the incline. This requires greater and greater friction for steeper slopes. Show that the maximum angle of an incline above the horizontal for which an object will not slide down is
  13. Calculate the maximum deceleration of a car that is heading down a [latex]6º[/latex] slope (one that makes an angle of [latex]6º[/latex] with the horizontal) under the following road conditions. You may assume that the weight of the car is evenly distributed on all four tires and that the coefficient of static friction is involved—that is, the tires are not allowed to slip during the deceleration. (Ignore rolling.) Calculate for a car: (a) On dry concrete. (b) On wet concrete. (c) On ice, assuming that [latex]{\mu }_{s}=0\text{.}\text{100}[/latex], the same as for shoes on ice.
  14. Calculate the maximum acceleration of a car that is heading up a
    [latex]\text{4º}[/latex] slope (one that makes an angle of
    [latex]\text{4º}[/latex] with the horizontal) under the following road conditions. Assume that only half the weight of the car is supported by the two drive wheels and that the coefficient of static friction is involved—that is, the tires are not allowed to slip during the acceleration. (Ignore rolling.) (a) On dry concrete. (b) On wet concrete. (c) On ice, assuming that
    [latex]{\text{μ}}_{\text{s}}=\phantom{\rule{0.25em}{0ex}}\text{0.100}[/latex], the same as for shoes on ice.
  15. Repeat Exercise 14 for a car with four-wheel drive.
  16. A freight train consists of two [latex]8\text{.}\text{00}×{\text{10}}^{5}\text{-kg}[/latex] engines and 45 cars with average masses of [latex]5\text{.}\text{50}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{kg}[/latex]. (a) What force must each engine exert backward on the track to accelerate the train at a rate of [latex]5\text{.}\text{00}×{\text{10}}^{-2}\phantom{\rule{0.25em}{0ex}}m/{s}^{2}[/latex] if the force of friction is [latex]7\text{.}\text{50}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}N[/latex], assuming the engines exert identical forces? This is not a large frictional force for such a massive system. Rolling friction for trains is small, and consequently trains are very energy-efficient transportation systems. (b) What is the magnitude of the force in the coupling between the 37th and 38th cars (this is the force each exerts on the other), assuming all cars have the same mass and that friction is evenly distributed among all of the cars and engines?
  17. Consider the 52.0-kg mountain climber in Figure 30.8. (a) Find the tension in the rope and the force that the mountain climber must exert with her feet on the vertical rock face to remain stationary. Assume that the force is exerted parallel to her legs. Also, assume negligible force exerted by her arms. (b) What is the minimum coefficient of friction between her shoes and the cliff?
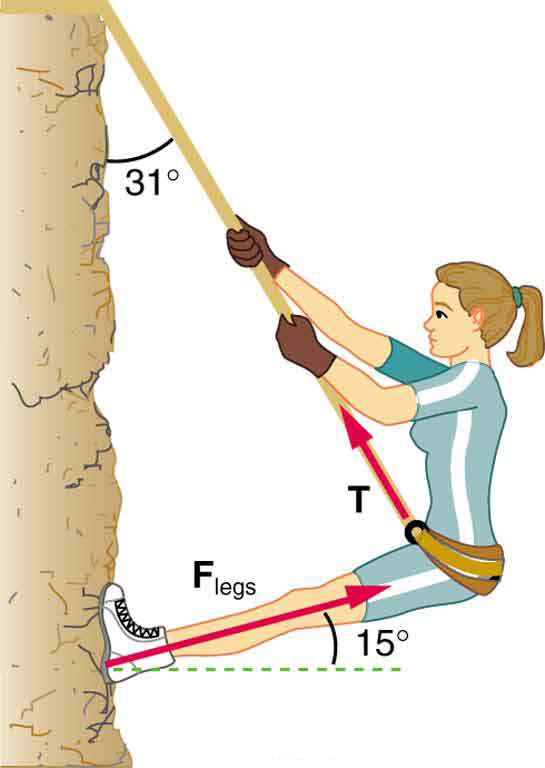
    A mountain climber with a mass of fifty two kilograms exerts force with her feet parallel to her legs on a vertical rock face to remain stationary. The angle between her legs and the rock face is fifteen degrees, whereas the angle between the rope and the cliff is thirty one degrees.
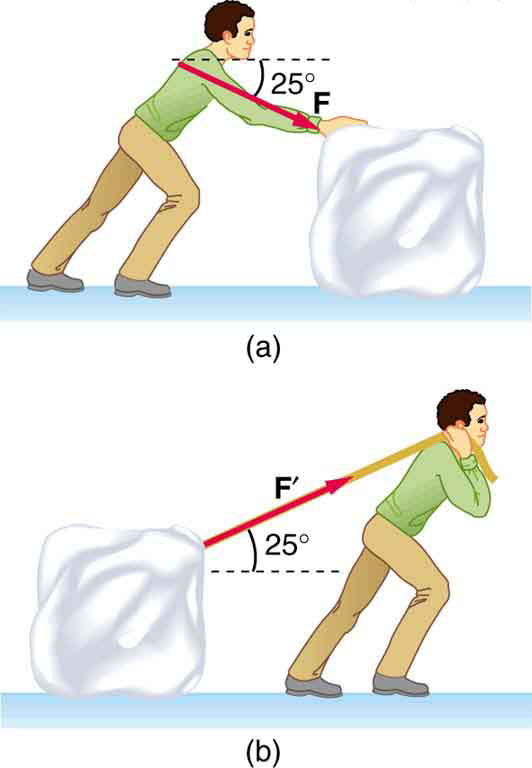
    Figure 30.8: Part of the climber’s weight is supported by her rope and part by friction between her feet and the rock face.
  18. A contestant in a winter sporting event pushes a 45.0-kg block of ice across a frozen lake as shown in Figure 30.9(a). (a) Calculate the minimum force [latex]F[/latex] he must exert to get the block moving. (b) What is the magnitude of its acceleration once it starts to move, if that force is maintained?
  19. Repeat Exercise 18 with the contestant pulling the block of ice with a rope over his shoulder at the same angle above the horizontal as shown in Figure 30.9(b).
(a) A block of ice is being pushed by a contestant in a winter sporting event across a frozen lake at an angle of twenty five degrees. (b) A block of ice is being pulled by a contestant in a winter sporting event across a frozen lake at an angle of twenty five degrees.
Figure 30.9: Which method of sliding a block of ice requires less force—(a) pushing or (b) pulling at the same angle above the horizontal?

Glossary

friction
a force that opposes relative motion or attempts at motion between systems in contact
kinetic friction
a force that opposes the motion of two systems that are in contact and moving relative to one another
static friction
a force that opposes the motion of two systems that are in contact and are not moving relative to one another
magnitude of static friction
[latex]{f}_{s}\le {\mu }_{s}\phantom{\rule{0.25em}{0ex}}N[/latex], where [latex]{\mu }_{s}[/latex] is the coefficient of static friction and [latex]N[/latex] is the magnitude of the normal force
magnitude of kinetic friction
[latex]{f}_{k}={\mu }_{k}N[/latex], where [latex]{\mu }_{k}[/latex] is the coefficient of kinetic friction
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book