"

Fluid Dynamics and Its Biological and Medical Applications

85 Flow Rate and Its Relation to Velocity

Learning Objectives

Flow Rate and Volume

In many biological systems, fluids must move efficiently and in a controlled way—blood must circulate through arteries and veins, air must flow in and out of the lungs, and nutrients must travel through the digestive system. A key quantity that describes how much fluid moves is the flow rate [latex]Q[/latex], defined as the volume of fluid passing through a specific location in a given amount of time (see Figure 85.1). Mathematically, we write:

[latex]Q = \frac{V}{t}[/latex]

where:

  • [latex]Q[/latex] is the flow rate,
  • [latex]V[/latex] is the volume of fluid, and
  • [latex]t[/latex] is the elapsed time.

The SI unit of flow rate is cubic meters per second ([latex]\text{m}^3/\text{s}[/latex]), but in medical and biological settings, liters per minute (L/min) or milliliters per second (mL/s) are more commonly used. For example, the heart of a healthy adult at rest typically pumps about 5.00 liters of blood per minute.

Remember that:

  • 1 liter (L) = [latex]10^{-3} \, \text{m}^3[/latex] = [latex]10^3 \, \text{cm}^3[/latex]

We will use whichever units are most convenient depending on the biological or medical context.

Visualizing Flow Rate

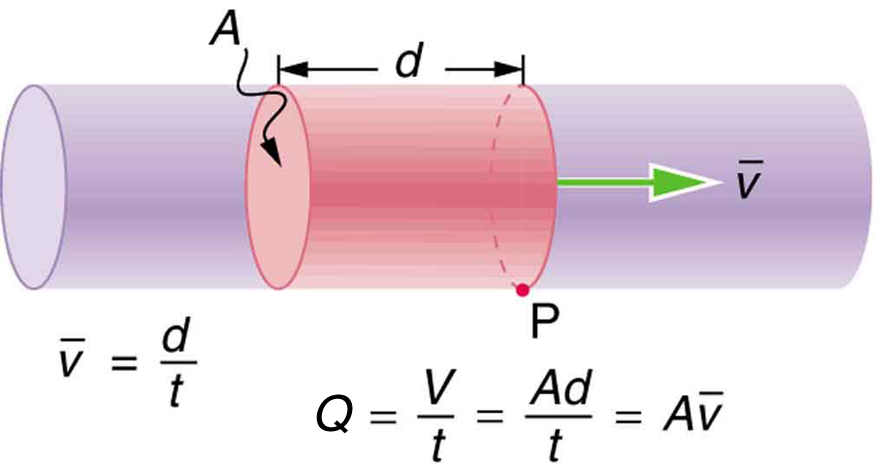
The figure shows a fluid flowing through a cylindrical pipe open at both ends. A portion of the cylindrical pipe with the fluid is shaded for a length d. The velocity of the fluid in the shaded region is shown by v toward the right. The cross sections of the shaded cylinder are marked as A. This cylinder of fluid flows past a point P on the cylindrical pipe. The velocity v is equal to d over t.
Figure 85.1Flow rate is the volume of fluid that passes through a point per unit time. In this diagram, the shaded volume of fluid moves past point [latex]P[/latex] in time [latex]t[/latex]. The volume is [latex]Ad[/latex], and the average velocity is [latex]\bar{v} = d/t[/latex], so the flow rate is:[latex]Q = \frac{Ad}{t} = A\bar{v}[/latex].

This formula is particularly useful in systems like blood vessels, airways, IV lines, and other tubular structures. It shows that the flow rate depends on both the cross-sectional area [latex]A[/latex] and the average velocity [latex]\bar{v}[/latex] of the fluid. If the vessel narrows (decreasing [latex]A[/latex]), the velocity must increase to keep the flow rate constant—an idea we’ll explore more deeply when we examine the equation of continuity.

Example 85.1 Calculating Volume from Flow Rate: The Heart Pumps a Lot of Blood in a Lifetime

How many cubic meters of blood does the heart pump in a 75-year lifetime, assuming the average flow rate is 5.00 L/min?

Strategy

Time and flow rate [latex]Q[/latex] are given, and so the volume [latex]V[/latex] can be calculated from the definition of flow rate.

Solution

Solving [latex]Q=V/t[/latex] for volume gives

[latex]V=\text{Qt}\text{.}[/latex]

Substituting known values yields

[latex]\begin{array}{lll}V& =& (\frac{5\text{.}\text{00}\phantom{\rule{0.25em}{0ex}}\text{L}}{\text{1 min}})(\text{75}\phantom{\rule{0.25em}{0ex}}\text{y})(\frac{1\phantom{\rule{0.25em}{0ex}}{\text{m}}^{3}}{{\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}\text{L}})(5\text{.}\text{26}×{\text{10}}^{5}\frac{\text{min}}{\text{y}})\\ \text{}& =& 2\text{.}0×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{3}\text{.}\end{array}[/latex]

Discussion

This amount is about 200,000 tons of blood. For comparison, this value is equivalent to about 200 times the volume of water contained in a 6-lane 50-m lap pool.

Flow Rate and Velocity: Not the Same Thing

Although flow rate and velocity are closely related, they are not the same physical quantity. To illustrate this, consider two rivers: one is narrow but flows quickly, and the other is wide but flows slowly. Which one moves more water per second? It depends not just on the speed of the water but also on how wide and deep the river is—that is, its cross-sectional area [latex]A[/latex]. The total volume of water moving per second (the flow rate) depends on both the speed [latex]\overline{v}[/latex] and the area through which the water flows (see Figure 85.1):

[latex]Q = A \overline{v}[/latex]

This relationship shows that the flow rate is directly proportional to both:

  • the cross-sectional area [latex]A[/latex] of the tube, vessel, or airway, and
  • the average velocity [latex]\overline{v}[/latex] of the fluid.

In biological systems, this equation has many applications. For example, if a blood vessel narrows due to plaque (as in atherosclerosis), the cross-sectional area decreases. If the body needs to maintain the same flow rate to supply tissues with oxygen, the velocity of the blood must increase. This can create higher pressure, contributing to cardiovascular strain.

The volume of fluid flowing through a segment of pipe or vessel can be visualized as a moving cylinder of fluid. If this cylinder has cross-sectional area [latex]A[/latex] and length [latex]d[/latex], then its volume is:

[latex]V = A d[/latex]

If it takes time [latex]t[/latex] for that volume to pass a point, then the average velocity is [latex]\overline{v} = d/t[/latex], and the flow rate becomes:

[latex]Q = \frac{V}{t} = \frac{Ad}{t} = A \overline{v}[/latex]

The Equation of Continuity

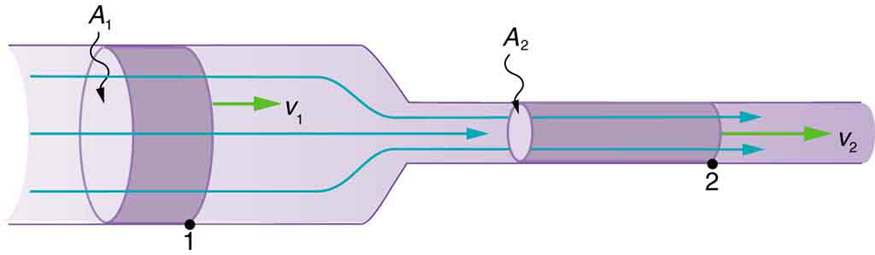
The figure shows a cylindrical tube broad at the left and narrow at the right. The fluid is shown to flow through the cylindrical tube toward right along the axis of the tube. A shaded area is marked on the broader cylinder on the left. A cross section is marked on it as A one. A point one is marked on this cross section. The velocity of the fluid through the shaded area on narrow tube is marked by v one as an arrow toward right. Another shaded area is marked on the narrow cylindrical on the right. The shaded area on narrow tube is longer than the one on broader tube to show that when a tube narrows, the same volume occupies a greater length. A cross section is marked on the narrow cylindrical tube as A two. A point two is marked on this cross section. The velocity of fluid through the shaded area on narrow tube is marked v two toward right. The arrow depicting v two is longer than for v one showing v two to be greater in value than v one.
Figure 85.2 A narrowing tube causes the fluid speed to increase. For the same volume to pass points 1 and 2 in the same amount of time, the fluid must move faster where the pipe is narrower. This illustrates the equation of continuity.. (Note that the relative volumes of the two cylinders and the corresponding velocity vector arrows are not drawn to scale.)

Figure 85.2 shows an incompressible fluid flowing along a pipe of decreasing radius. Because liquids are incompressible fluids, the same amount of fluid must pass every point in a closed system over time. This requirement leads to the equation of continuity, which states that:

[latex]Q_1 = Q_2[/latex]
[latex]A_1 \overline{v}_1 = A_2 \overline{v}_2[/latex]

Here:

  • [latex]A_1[/latex] and [latex]A_2[/latex] are the cross-sectional areas at two different points in the system,
  • [latex]\overline{v}_1[/latex] and [latex]\overline{v}_2[/latex] are the average fluid velocities at those points.

This equation explains why water exits a narrow nozzle faster than it does from a wide hose: the fluid accelerates to maintain the same flow rate. Similarly, in medicine, blood accelerates through narrowed arteries, a condition that can be detected with Doppler ultrasound by measuring flow velocities.

Important Notes About Gases

The equation of continuity works well for liquids, which are nearly incompressible. For gases, which are compressible, the equation must be used with care. If the gas density remains constant (as in low-speed respiratory airflow), the equation still holds. But in high-speed jets or ventilators, where pressure changes significantly, the gas compressibility must be taken into account.

Example 85.2 Calculating Fluid Speed: Speed Increases When a Tube Narrows

A nozzle with a radius of 0.250 cm is attached to a garden hose with a radius of 0.900 cm. The flow rate through hose and nozzle is 0.500 L/s. Calculate the speed of the water (a) in the hose and (b) in the nozzle.

Strategy

We can use the relationship between flow rate and speed to find both velocities. We will use the subscript 1 for the hose and 2 for the nozzle.

Solution for (a)

First, we solve [latex]Q=A\overline{v}[/latex] for [latex]{v}_{1}[/latex] and note that the cross-sectional area is [latex]A={\mathrm{\pi r}}^{2}[/latex], yielding

[latex]{\overline{v}}_{1}=\frac{Q}{{A}_{1}}=\frac{Q}{{\mathrm{\pi r}}_{1}^{2}}\text{.}[/latex]

Substituting known values and making appropriate unit conversions yields

[latex]{\overline{v}}_{1}=\frac{(0\text{.}\text{500}\phantom{\rule{0.25em}{0ex}}\text{L/s})({\text{10}}^{-3}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{3}/\text{L})}{\pi (9\text{.}\text{00}×{\text{10}}^{-3}\phantom{\rule{0.25em}{0ex}}\text{m}{)}^{2}}=1\text{.}\text{96}\phantom{\rule{0.25em}{0ex}}\text{m/s}\text{.}[/latex]

Solution for (b)

We could repeat this calculation to find the speed in the nozzle [latex]{\overline{v}}_{2}[/latex], but we will use the equation of continuity to give a somewhat different insight. Using the equation which states

[latex]{A}_{1}{\overline{v}}_{1}={A}_{2}{\overline{v}}_{2}\text{,}[/latex]

solving for [latex]{\overline{v}}_{2}[/latex] and substituting [latex]{\mathrm{\pi r}}^{2}[/latex] for the cross-sectional area yields

[latex]{\overline{v}}_{2}=\frac{{A}_{1}}{{A}_{2}}{\overline{v}}_{1}=\frac{{\mathrm{\pi r}}_{1}^{2}}{{\mathrm{\pi r}}_{2}^{2}}{\overline{v}}_{1}=\frac{{r}_{{1}^{2}}}{{r}_{{2}^{2}}}{\overline{v}}_{1}\text{.}[/latex]

Substituting known values,

[latex]{\overline{v}}_{2}=\frac{(0\text{.}\text{900}\phantom{\rule{0.25em}{0ex}}\text{cm}{)}^{2}}{(0\text{.}\text{250}\phantom{\rule{0.25em}{0ex}}\text{cm}{)}^{2}}1\text{.}\text{96}\phantom{\rule{0.25em}{0ex}}\text{m/s}=\text{25}\text{.}\text{5 m/s}\text{.}[/latex]

Discussion

A speed of 1.96 m/s is about right for water emerging from a nozzleless hose. The nozzle produces a considerably faster stream merely by constricting the flow to a narrower tube.

Flow Speed and Tube Radius

The equation of continuity shows that as the cross-sectional area of a tube decreases, the speed of the fluid increases. Since the area [latex]A[/latex] of a circular tube depends on the square of its radius ([latex]A = \pi r^2[/latex]), we find that:

[latex]v \propto \frac{1}{r^2}[/latex]

This relationship means that a small change in radius can have a large effect on flow speed. A familiar example is blowing out a candle: when you purse your lips, you reduce the radius of your mouth opening, dramatically increasing the velocity of the air. In contrast, blowing with an open mouth distributes the air more widely and reduces its speed, making it much less effective at extinguishing the flame.

Branching Flow in the Cardiovascular System

In many biological systems, including the cardiovascular system, fluid flow doesn’t just pass through a single pipe—it branches. Blood is pumped from the heart into large arteries, which split into smaller arteries, then into even finer vessels called capillaries. Although the individual vessels become smaller, the total cross-sectional area increases dramatically due to the sheer number of capillaries.

To conserve flow rate across such branches, the equation of continuity is extended. Instead of just comparing flow at two points, we consider the total number of branches [latex]n[/latex] in each section:

[latex]n_1 A_1 \overline{v}_1 = n_2 A_2 \overline{v}_2[/latex]

Here:

  • [latex]n_1[/latex] and [latex]n_2[/latex] are the number of vessels in two regions,
  • [latex]A_1[/latex] and [latex]A_2[/latex] are the cross-sectional areas of each vessel in those regions, and
  • [latex]\overline{v}_1[/latex] and [latex]\overline{v}_2[/latex] are the average flow velocities.

This form of the continuity equation shows that while individual capillaries are narrow and flow within them is slow, their sheer number ensures that the total flow rate remains constant throughout the circulatory system. This slower speed in capillaries is essential for efficient gas and nutrient exchange with surrounding tissues.

In medical diagnostics, these principles are critical. For instance, in conditions like arteriosclerosis, where vessel radii narrow significantly, flow speed and pressure can change dramatically. Understanding how flow velocity scales with radius and how branching affects total flow is fundamental for interpreting circulatory health.

Example 85.3 Calculating Flow Speed and Vessel Diameter: Branching in the Cardiovascular System

The aorta is the principal blood vessel through which blood leaves the heart in order to circulate around the body. (a) Calculate the average speed of the blood in the aorta if the flow rate is 5.0 L/min. The aorta has a radius of 10 mm. (b) Blood also flows through smaller blood vessels known as capillaries. When the rate of blood flow in the aorta is 5.0 L/min, the speed of blood in the capillaries is about 0.33 mm/s. Given that the average diameter of a capillary is [latex]8.0\phantom{\rule{0.25em}{0ex}}\mu \text{m}[/latex], calculate the number of capillaries in the blood circulatory system.

Strategy

We can use [latex]Q=A\overline{v}[/latex] to calculate the speed of flow in the aorta and then use the general form of the equation of continuity to calculate the number of capillaries as all of the other variables are known.

Solution for (a)

The flow rate is given by [latex]Q=A\overline{v}[/latex] or [latex]\overline{v}=\frac{Q}{{\mathrm{\pi r}}^{2}}[/latex] for a cylindrical vessel.

Substituting the known values (converted to units of meters and seconds) gives

[latex]\overline{v}=\frac{(5.0\phantom{\rule{0.25em}{0ex}}\text{L/min})({\text{10}}^{-3}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{3}\text{/L})(1\phantom{\rule{0.25em}{0ex}}\text{min/}\text{60}\phantom{\rule{0.25em}{0ex}}\text{s})}{\pi {(0\text{.}\text{010 m})}^{2}}=0\text{.}\text{27}\phantom{\rule{0.25em}{0ex}}\text{m/s}.[/latex]

Solution for (b)

Using [latex]{n}_{1}{A}_{1}{\overline{v}}_{1}={n}_{2}{A}_{2}{\overline{v}}_{1}[/latex], assigning the subscript 1 to the aorta and 2 to the capillaries, and solving for [latex]{n}_{2}[/latex] (the number of capillaries) gives [latex]{n}_{2}=\frac{{n}_{1}{A}_{1}{\overline{v}}_{1}}{{A}_{2}{\overline{v}}_{2}}[/latex]. Converting all quantities to units of meters and seconds and substituting into the equation above gives

[latex]{n}_{2}=\frac{\left(1\right)\left(\pi \right){\left(\text{10}×{\text{10}}^{-3}\phantom{\rule{0.25em}{0ex}}\text{m}\right)}^{2}\left(0.27 m/s\right)}{\left(\pi \right){\left(4.0×{\text{10}}^{-6}\phantom{\rule{0.25em}{0ex}}\text{m}\right)}^{2}\left(0.33×{\text{10}}^{-3}\phantom{\rule{0.25em}{0ex}}\text{m/s}\right)}=5.0×{\text{10}}^{9}\phantom{\rule{0.25em}{0ex}}\text{capillaries}.[/latex]

Discussion

Note that the speed of flow in the capillaries is considerably reduced relative to the speed in the aorta due to the significant increase in the total cross-sectional area at the capillaries. This low speed is to allow sufficient time for effective exchange to occur although it is equally important for the flow not to become stationary in order to avoid the possibility of clotting. Does this large number of capillaries in the body seem reasonable? In active muscle, one finds about 200 capillaries per [latex]{\text{mm}}^{3}[/latex], or about [latex]\text{200}×{\text{10}}^{6}[/latex] per 1 kg of muscle. For 20 kg of muscle, this amounts to about [latex]4×{\text{10}}^{9}[/latex] capillaries.

Section Summary

  • Flow rate [latex]Q[/latex] is the volume [latex]V[/latex] of fluid that passes a given point in a time interval [latex]t[/latex], defined by:
    [latex]Q = \frac{V}{t}[/latex]
  • The SI unit of volume is cubic meters: [latex]\text{m}^3[/latex].
  • A common alternative unit for fluid volume is the liter (L), where:
    [latex]1 \, \text{L} = 10^{-3} \, \text{m}^3[/latex]
  • Flow rate is related to average velocity [latex]\overline{v}[/latex] and cross-sectional area [latex]A[/latex] of the tube by:
    [latex]Q = A \overline{v}[/latex]
  • For incompressible fluids, flow rate is conserved across any two points in a system. This is the equation of continuity:
    [latex]\begin{array}{c} Q_1 = Q_2 \\ A_1 \overline{v}_1 = A_2 \overline{v}_2 \\ n_1 A_1 \overline{v}_1 = n_2 A_2 \overline{v}_2 \end{array}[/latex]

    where [latex]n_1[/latex] and [latex]n_2[/latex] are the number of branches in each section (as seen in capillary and arterial systems).

Conceptual Questions

  1. What is the difference between flow rate and fluid velocity? How are they related?
  2. Many figures in the text show streamlines. Explain why fluid velocity is greatest where streamlines are closest together. (Hint: Consider the relationship between fluid velocity and the cross-sectional area through which it flows.)
  3. Identify some substances that are incompressible and some that are not.

Problems & Exercises

  1. What is the average flow rate in [latex]{\text{cm}}^{3}\text{/s}[/latex] of gasoline to the engine of a car traveling at 100 km/h if it averages 10.0 km/L?
  2. The heart of a resting adult pumps blood at a rate of 5.00 L/min. (a) Convert this to [latex]{\text{cm}}^{3}\text{/s}[/latex]. (b) What is this rate in [latex]{\text{m}}^{3}\text{/s}[/latex]?
  3. Blood is pumped from the heart at a rate of 5.0 L/min into the aorta (of radius 1.0 cm). Determine the speed of blood through the aorta.
  4. Blood is flowing through an artery of radius 2 mm at a rate of 40 cm/s. Determine the flow rate and the volume that passes through the artery in a period of 30 s.
  5. The Huka Falls on the Waikato River is one of New Zealand’s most visited natural tourist attractions (see Figure 85.3). On average the river has a flow rate of about 300,000 L/s. At the gorge, the river narrows to 20 m wide and averages 20 m deep. (a) What is the average speed of the river in the gorge? (b) What is the average speed of the water in the river downstream of the falls when it widens to 60 m and its depth increases to an average of 40 m?
    Water rushes over a fall.
    Figure 85.3 The Huka Falls in Taupo, New Zealand, demonstrate flow rate. (credit: RaviGogna, Flickr)
  6. A major artery with a cross-sectional area of [latex]1\text{.}\text{00}\phantom{\rule{0.25em}{0ex}}{\text{cm}}^{2}[/latex] branches into 18 smaller arteries, each with an average cross-sectional area of [latex]0\text{.}\text{400}\phantom{\rule{0.25em}{0ex}}{\text{cm}}^{2}[/latex]. By what factor is the average velocity of the blood reduced when it passes into these branches?
  7. (a) As blood passes through the capillary bed in an organ, the capillaries join to form venules (small veins). If the blood speed increases by a factor of 4.00 and the total cross-sectional area of the venules is [latex]\text{10}\text{.}0\phantom{\rule{0.25em}{0ex}}{\text{cm}}^{2}[/latex], what is the total cross-sectional area of the capillaries feeding these venules? (b) How many capillaries are involved if their average diameter is [latex]10.0\phantom{\rule{0.25em}{0ex}}\mu \text{m}[/latex]?
  8. The human circulation system has approximately [latex]1×{\text{10}}^{9}[/latex] capillary vessels. Each vessel has a diameter of about [latex]8\phantom{\rule{0.25em}{0ex}}\mu \text{m}[/latex]. Assuming cardiac output is 5 L/min, determine the average velocity of blood flow through each capillary vessel.
  9. (a) Estimate the time it would take to fill a private swimming pool with a capacity of 80,000 L using a garden hose delivering 60 L/min. (b) How long would it take to fill if you could divert a moderate size river, flowing at [latex]\text{5000}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{3}\text{/s}[/latex], into it?
  10. The flow rate of blood through a [latex]2\text{.}\text{00}×{\text{10}}^{\text{–6}}\text{-m}[/latex] -radius capillary is [latex]3\text{.}\text{80}×{\text{10}}^{9}\phantom{\rule{0.25em}{0ex}}{\text{cm}}^{3}\text{/s}[/latex]. (a) What is the speed of the blood flow? (This small speed allows time for diffusion of materials to and from the blood.) (b) Assuming all the blood in the body passes through capillaries, how many of them must there be to carry a total flow of [latex]90\text{.}0\phantom{\rule{0.25em}{0ex}}{\text{cm}}^{3}\text{/s}[/latex]? (The large number obtained is an overestimate, but it is still reasonable.)
  11. (a) What is the fluid speed in a fire hose with a 9.00-cm diameter carrying 80.0 L of water per second? (b) What is the flow rate in cubic meters per second? (c) Would your answers be different if salt water replaced the fresh water in the fire hose?
  12. The main uptake air duct of a forced air gas heater is 0.300 m in diameter. What is the average speed of air in the duct if it carries a volume equal to that of the house’s interior every 15 min? The inside volume of the house is equivalent to a rectangular solid 13.0 m wide by 20.0 m long by 2.75 m high.
  13. Water is moving at a velocity of 2.00 m/s through a hose with an internal diameter of 1.60 cm. (a) What is the flow rate in liters per second? (b) The fluid velocity in this hose’s nozzle is 15.0 m/s. What is the nozzle’s inside diameter?
  14. Prove that the speed of an incompressible fluid through a constriction, such as in a Venturi tube, increases by a factor equal to the square of the factor by which the diameter decreases. (The converse applies for flow out of a constriction into a larger-diameter region.)
  15. Water emerges straight down from a faucet with a 1.80-cm diameter at a speed of 0.500 m/s. (Because of the construction of the faucet, there is no variation in speed across the stream.) (a) What is the flow rate in [latex]{\text{cm}}^{3}\text{/s}[/latex]? (b) What is the diameter of the stream 0.200 m below the faucet? Neglect any effects due to surface tension.
  16. Unreasonable Results A mountain stream is 10.0 m wide and averages 2.00 m in depth. During the spring runoff, the flow in the stream reaches [latex]\text{100,000}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{3}\text{/s}[/latex]. (a) What is the average velocity of the stream under these conditions? (b) What is unreasonable about this velocity? (c) What is unreasonable or inconsistent about the premises?

Glossary

flow rate
abbreviated Q, it is the volume V that flows past a particular point during a time t, or Q = V/t
liter
a unit of volume, equal to 10−3 m3
incomprensible fluids
fluids whose density does not change significantly when pressure is applied. In many physics problems, liquids such as water are treated as incompressible to simplify calculations, meaning their volume remains essentially constant under pressure. This approximation is useful in analyzing fluid dynamics, such as flow through pipes or the cardiovascular system.
equation of continuity
a fundamental principle of fluid dynamics that states the mass flow rate of an incompressible fluid remains constant from one cross-section of a pipe to another. It is mathematically expressed as:
[latex]A_1v_1 = A_2v_2[/latex]
where [latex]A[/latex] is the cross-sectional area and [latex]v[/latex] is the fluid velocity. This equation shows that if the area of a pipe narrows, the fluid speed increases, and vice versa, assuming the fluid is incompressible and there is no accumulation of fluid.
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book