"

Uniform Circular Motion and Gravitation

38 Fictitious Forces and Non-inertial Frames: The Coriolis Force

Learning Objectives

  • Distinguish between inertial and non-inertial frames of reference.

  • Understand the origin and effects of fictitious forces, including the centrifugal and Coriolis forces.

  • Describe how the Coriolis force influences large-scale natural phenomena like hurricanes.

Fictitious Forces and Accelerated Frames

Experiences such as taking off in a jet, making a sharp turn in a car, or riding a merry-go-round all involve fictitious forces—forces that seem real but arise solely from observing motion in an accelerating or rotating frame of reference.

Inertial vs. Non-Inertial Frames

An inertial frame of reference is one in which Newton’s laws hold in their simplest form, and all forces have identifiable physical origins. For example, Earth is typically considered an approximately inertial frame, especially for most terrestrial motion.

In contrast, a non-inertial frame of reference is one that is accelerating. Observers in such frames perceive fictitious forces to explain observed motion. These forces do not arise from any physical interaction, but instead from the acceleration of the observer’s frame.

🚗 Turning in a Car

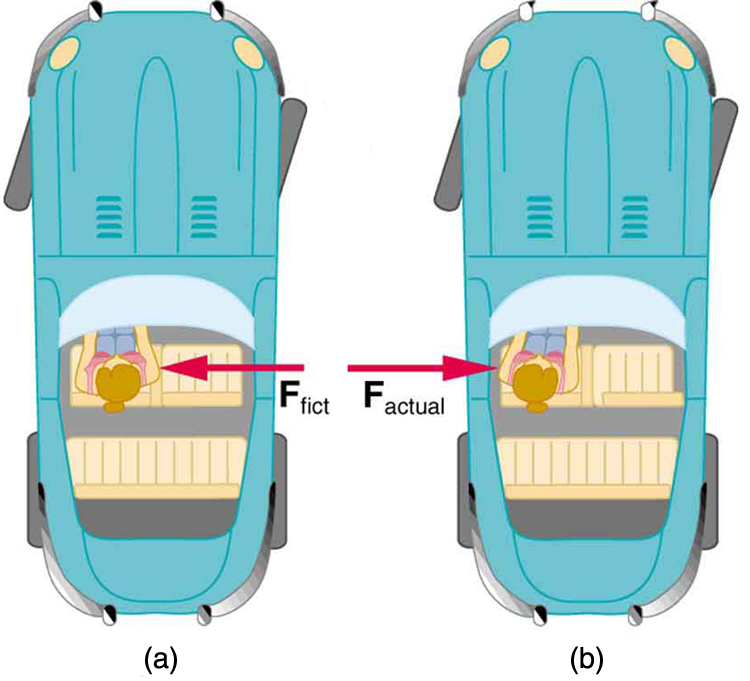
When a car makes a right turn, passengers feel as if they’re being pushed to the left. In the car’s frame (non-inertial), this appears to be a real force. However, in Earth’s frame (Figure 38.1), the car is simply accelerating rightward beneath the passengers, and no leftward force actually exists.

In figure a, there is a girl driving a car turning toward right. A fictitious force vector is acting on her body toward left. In figure b, the actual force vector acting on the girl’s body is shown toward right.
Figure 38.1: (a) The car driver feels herself forced to the left relative to the car when she makes a right turn. This is a fictitious force arising from the use of the car as a frame of reference. (b) In the Earth’s frame of reference, the driver moves in a straight line, obeying Newton’s first law, and the car moves to the right. There is no real force to the left on the driver relative to Earth. There is a real force to the right on the car to make it turn.

🎠 Riding a Merry-Go-Round

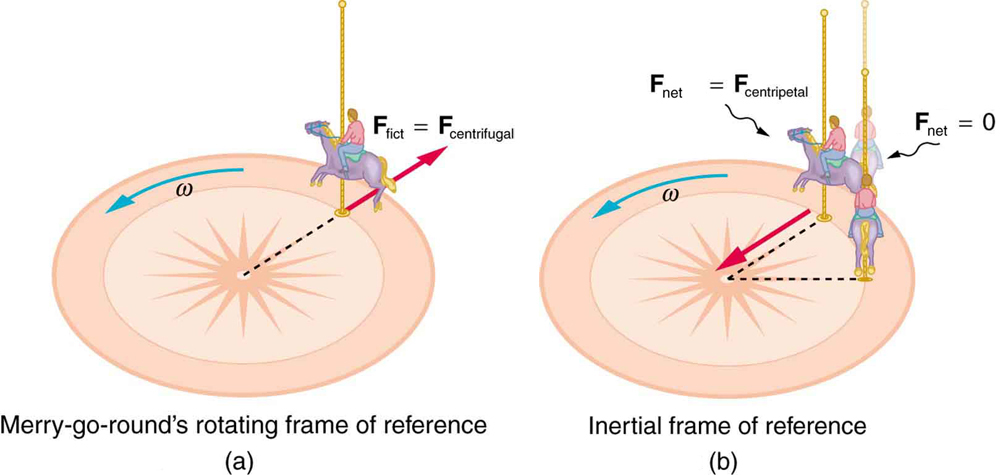
On a rotating merry-go-round (Figure 38.2), riders feel a force trying to fling them outward. This is called centrifugal force, a fictitious force that explains the rider’s motion within the rotating frame. In the inertial (Earth) frame, the rider’s inertia causes them to move in a straight line, and it is the centripetal force (e.g., from the handrail) that keeps them moving in a circle.

In figure a, looking down on the counterclockwise rotation of a merry-go-round, we see a child sitting on a horse rotating in counterclockwise direction with angular velocity omega. The fictious force is equal to the centrifugal force at the point of contact between the pole carrying horse and the merry-go-round surface, which is from the center of the round base toward outside. This is the merry-go-round’s rotating frame of reference. In figure b, the merry-go-round’s inertial frame of reference is given, where two horses carrying children are seen rotating with angular velocity omega in the counterclockwise direction. The net force of first horse is equal to the centripetal force, shown here with an arrow from the first horse toward the center of the circular base. A shadow of the second horse is shown going past the right side of the first horse in straight direction, whose net force is equal to zero. A dotted line from second as well as first horse are shown meeting at the center point making an angle.
Figure 38.2: (a) A rider on a merry-go-round feels as if he is being thrown off. This fictitious force is called the centrifugal force—it explains the rider’s motion in the rotating frame of reference. (b) In an inertial frame of reference and according to Newton’s laws, it is his inertia that carries him off and not a real force (the unshaded rider has [latex]{F}_{\text{net}}=0[/latex] and heads in a straight line). A real force, [latex]{F}_{\text{centripetal}}[/latex], is needed to cause a circular path.

The Centrifuge: Inertia in Action

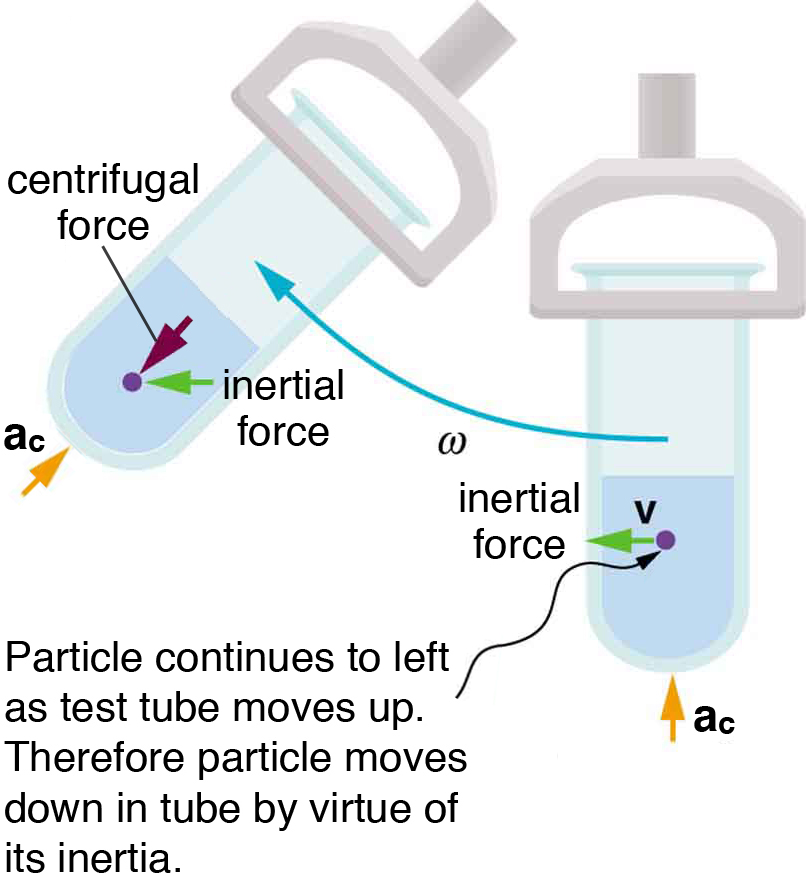
A centrifuge (Figure 38.3) spins rapidly to accelerate particles radially outward due to their inertia. In the centrifuge’s rotating frame, this is explained using a fictitious centrifugal force. In an inertial frame, the test tube provides the centripetal force that keeps particles in circular motion, while inertia causes sedimentation toward the walls.

A test tube is fitted in a centrifuge. The centrifuge is rotating toward the left. The inertial force vector on a particle inside the liquid is directed toward the left. The centrifugal force is directed toward the bottom of the test tube. The angular velocity is marked as omega.
Figure 38.3: Centrifuges use inertia to perform their task. Particles in the fluid sediment come out because their inertia carries them away from the center of rotation. The large angular velocity of the centrifuge quickens the sedimentation. Ultimately, the particles will come into contact with the test tube walls, which will then supply the centripetal force needed to make them move in a circle of constant radius.

The Coriolis Force

Now consider what happens when an object moves within a rotating frame.

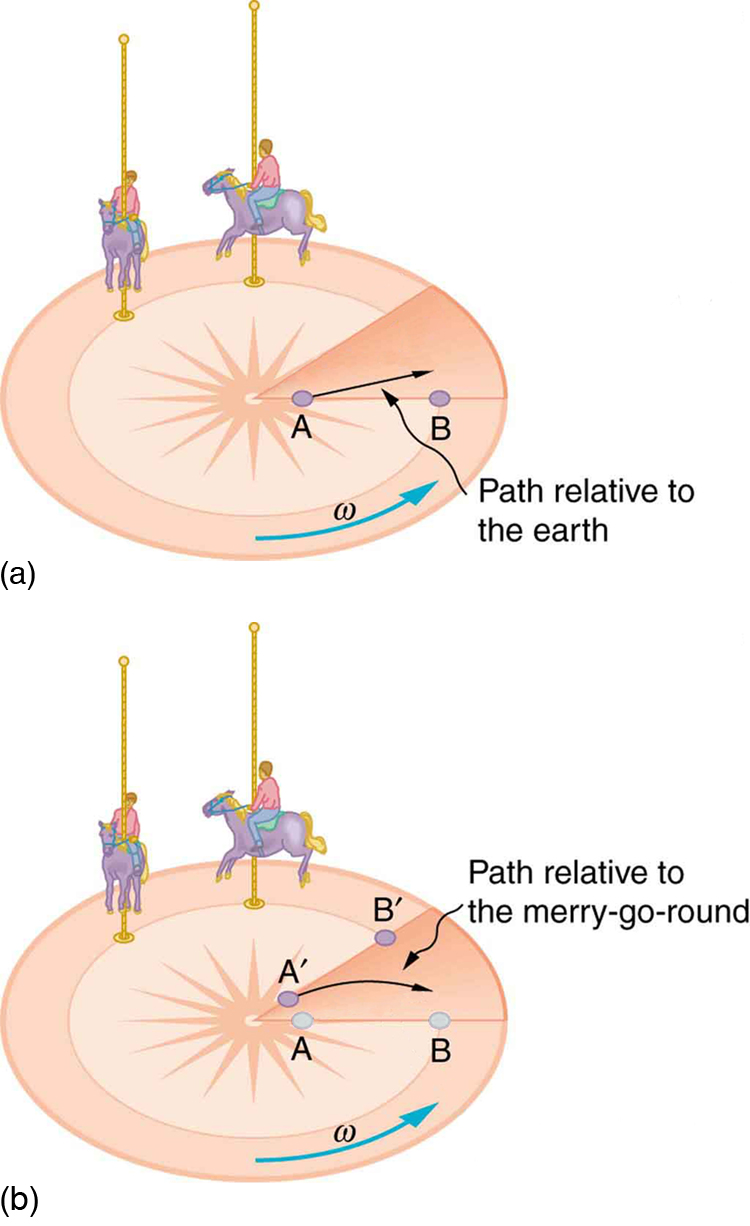
Imagine sliding a ball straight outward from the center of a spinning merry-go-round. In the Earth frame, the ball travels in a straight path. However, observers on the rotating platform (Figure 38.4?) see the ball curve to the right. This apparent curvature is explained by a fictitious force called the Coriolis force.

In the figure, a child on a merry-go-round is shown. A person slides a ball from the center from the point A toward the point B. The path covered by the ball on the merry-go-round is shown, which is a curved path. The ball reaches a point away from the point B.
Figure 38.4: Looking down on the counterclockwise rotation of a merry-go-round, we see that a ball slid straight toward the edge follows a path curved to the right. The person slides the ball toward point B, starting at point A. Both points rotate to the shaded positions (A’ and B’) shown in the time that the ball follows the curved path in the rotating frame and a straight path in Earth’s frame.

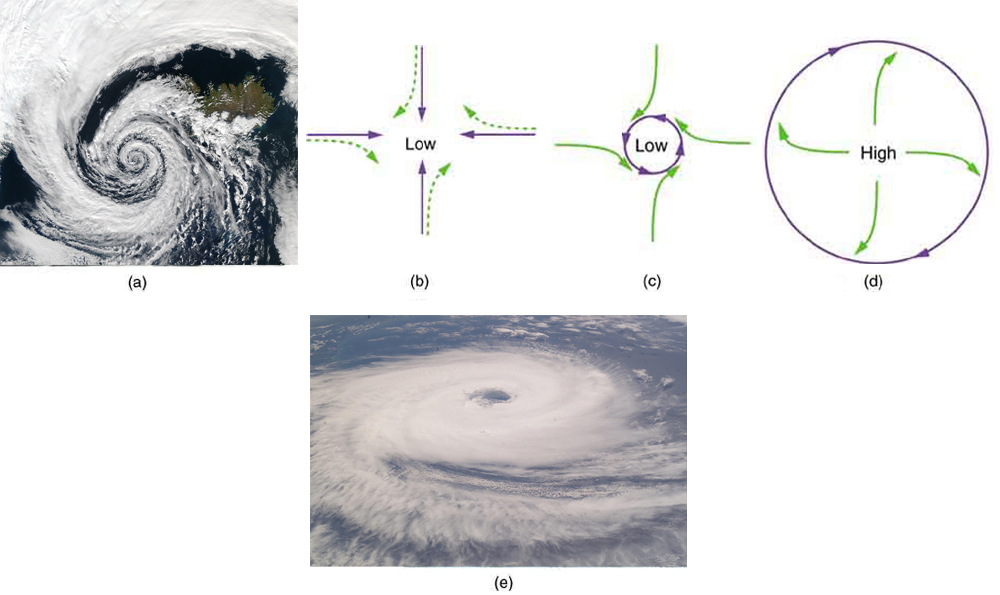
🌀 Coriolis Force in Earth Systems

Earth itself is a slowly rotating frame. While often negligible, its rotation does produce observable effects over large distances and timescales. For example:

  • In the Northern Hemisphere, the Coriolis force deflects moving air to the right.

  • In the Southern Hemisphere, it deflects air to the left.

This deflection leads to the counterclockwise rotation of hurricanes in the north and clockwise rotation in the south (Figure 38.5).

Figure a is a satellite photo of a hurricane rotating in counterclockwise direction. Figures b, c, and d are diagrams. In figure b, there are four arrows directed toward a low pressure zone at a point from North, East, West and South. Near each arrow there is a green dotted vector turned toward right at its arrow head which shows the direction of Coriolis force. In figure c, there is a small circle directed counter clockwise over the low pressure zone, which shows that the winds are deflected by Coriolis force. In figure d, a high-pressure zone is shown. Around it there are four green vectors directed toward their right near the arrow head. Figure e is a satellite photo of a tropical cyclone in the southern hemisphere. The direction of this cyclone is clockwise.
Figure 38.5: (a) The counterclockwise rotation of this northern hemisphere hurricane is a major consequence of the Coriolis force. (credit: NASA) (b) Without the Coriolis force, air would flow straight into a low-pressure zone, such as that found in tropical cyclones. (c) The Coriolis force deflects the winds to the right, producing a counterclockwise rotation. (d) Wind flowing away from a high-pressure zone is also deflected to the right, producing a clockwise rotation. (e) The opposite direction of rotation is produced by the Coriolis force in the southern hemisphere, leading to tropical cyclones. (credit: NASA)

Section Summary

  • Fictitious forces (centrifugal, Coriolis) arise only in non-inertial frames.

  • In an inertial frame, Newton’s laws explain motion without invoking fictitious forces.

  • The centrifugal force explains outward motion in a rotating frame.

  • The Coriolis force explains the deflection of moving objects in a rotating frame.

Despite being “fictitious,” these forces are useful for making sense of motion within accelerating frames, and they are mathematically necessary for applying Newton’s laws in such contexts.

Conceptual Questions

  1. When a toilet is flushed or a sink is drained, the water (and other material) begins to rotate about the drain on the way down. Assuming no initial rotation and a flow initially directly straight toward the drain, explain what causes the rotation and which direction it has in the northern hemisphere. (Note that this is a small effect and in most toilets the rotation is caused by directional water jets.) Would the direction of rotation reverse if water were forced up the drain?
  2. Is there a real force that throws water from clothes during the spin cycle of a washing machine? Explain how the water is removed.
  3. In one amusement park ride, riders enter a large vertical barrel and stand against the wall on its horizontal floor. The barrel is spun up and the floor drops away. Riders feel as if they are pinned to the wall by a force something like the gravitational force. This is a fictitious force sensed and used by the riders to explain events in the rotating frame of reference of the barrel. Explain in an inertial frame of reference (Earth is nearly one) what pins the riders to the wall, and identify all of the real forces acting on them.
  4. Action at a distance, such as is the case for gravity, was once thought to be illogical and therefore untrue. What is the ultimate determinant of the truth in physics, and why was this action ultimately accepted?
  5. Two friends are having a conversation. Anna says a satellite in orbit is in freefall because the satellite keeps falling toward Earth. Tom says a satellite in orbit is not in freefall because the acceleration due to gravity is not 9.80 [latex]{\text{m/s}}^{2}[/latex]. Who do you agree with and why?
  6. A non-rotating frame of reference placed at the center of the Sun is very nearly an inertial one. Why is it not exactly an inertial frame?

Glossary

fictitious force
a force having no physical origin
centrifugal force
a fictitious force that tends to throw an object off when the object is rotating in a non-inertial frame of reference
Coriolis force
the fictitious force causing the apparent deflection of moving objects when viewed in a rotating frame of reference
non-inertial frame of reference
an accelerated frame of reference
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book