There is another way to express the second law of thermodynamics, using the concept of entropy. This approach highlights how energy spreads out in a system and becomes less available to do useful work. The direction of natural processes—such as heat flowing from hot to cold—is consistent with a general trend toward increasing disorder. In thermodynamics, this disorder is captured by the concept of entropy, a state function that quantifies the unavailability of energy for work.

The definition of entropy becomes clearer when we revisit the Carnot engine. In a reversible cycle, the heat input and output are related to their respective temperatures by the equation:

Rearranging gives:

This ratio of heat transfer to temperature defines the change in entropy [latex]\Delta S[/latex] for a reversible process:

Here, [latex]Q[/latex] is positive when heat is added to the system and negative when heat is removed. [latex]T[/latex] is the absolute temperature (in kelvin) at which the process occurs. Entropy has SI units of joules per kelvin (J/K). If the temperature changes gradually during a process, you can often approximate [latex]T[/latex] as the average temperature over the interval. For precise calculations, especially with large temperature changes, you would need to integrate over the process.

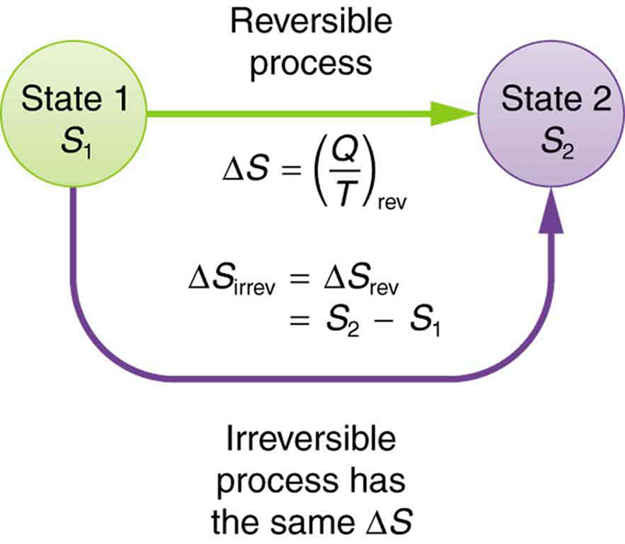
This definition applies strictly to reversible processes. However, it’s also useful for real, irreversible processes because entropy, like internal energy, is a state function—it depends only on the initial and final states of the system, not the path taken. So to find [latex]\Delta S[/latex] for an irreversible process, we can imagine a reversible path between the same two states and calculate the change that way.

Let’s examine the change in entropy for a complete Carnot cycle, including the hot and cold reservoirs. The hot reservoir loses entropy:

because heat leaves it. The cold reservoir gains entropy:

since heat is added to it. The total entropy change for the system is:

Substituting the previous expressions and using the relation between [latex]Q_{\text{h}}[/latex] and [latex]Q_{\text{c}}[/latex] gives:

This confirms a general result: for any reversible process, the total change in entropy is zero.

While individual parts of a system may gain or lose entropy, the total entropy change of the system and surroundings is zero during a reversible transformation. This is often summarized by stating that reversible processes do not affect the total entropy of the universe.

However, real processes are irreversible and do increase the entropy of the universe. Still, we can use a hypothetical reversible path to calculate entropy changes for real processes, which is helpful for understanding energy flow in biological systems, environmental processes, and thermodynamic machines like engines and refrigerators.

Example 113.1 Entropy Increases in an Irreversible (Real) Process

Spontaneous heat transfer from hot to cold is an irreversible process. Calculate the total change in entropy if 4000 J of heat transfer occurs from a hot reservoir at [latex]{T}_{\text{h}}=\text{600 K}\left(\text{327º C}\right)[/latex] to a cold reservoir at [latex]{T}_{\text{c}}=\text{250 K}\left(-\text{23º C}\right)[/latex], assuming there is no temperature change in either reservoir. (See Figure 113.3.)

Strategy

How can we calculate the change in entropy for an irreversible process when [latex]\Delta {S}_{\text{tot}}=\Delta {S}_{\text{h}}+\Delta {S}_{\text{c}}[/latex] is valid only for reversible processes? Remember that the total change in entropy of the hot and cold reservoirs will be the same whether a reversible or irreversible process is involved in heat transfer from hot to cold. So we can calculate the change in entropy of the hot reservoir for a hypothetical reversible process in which 4000 J of heat transfer occurs from it; then we do the same for a hypothetical reversible process in which 4000 J of heat transfer occurs to the cold reservoir. This produces the same changes in the hot and cold reservoirs that would occur if the heat transfer were allowed to occur irreversibly between them, and so it also produces the same changes in entropy.

Solution

We now calculate the two changes in entropy using [latex]\Delta {S}_{\text{tot}}=\Delta {S}_{\text{h}}+\Delta {S}_{\text{c}}[/latex]. First, for the heat transfer from the hot reservoir,

[latex]\Delta {S}_{\text{h}}=\frac{-{Q}_{\text{h}}}{{T}_{\text{h}}}=\frac{-\text{4000 J}}{\text{600 K}}=–6\text{.}\text{67 J/K}\text{.}[/latex]

And for the cold reservoir,

[latex]\Delta {S}_{\text{c}}=\frac{{Q}_{\text{c}}}{{T}_{\text{c}}}=\frac{\text{4000 J}}{\text{250 K}}=\text{16}\text{.}0 J/K\text{.}[/latex]

Thus the total is

[latex]\begin{array}{ccc}\Delta {S}_{\text{tot}}& =& \Delta {S}_{\text{h}}+\Delta {S}_{\text{c}}\\ & =& \left(–6\text{.}\text{67 +16}\text{.}0\right)\phantom{\rule{0.25em}{0ex}}\text{J/K}\\ & =& \text{9.33 J/K.}\end{array}[/latex]

Discussion

There is an increase in entropy for the system of two heat reservoirs undergoing this irreversible heat transfer. We will see that this means there is a loss of ability to do work with this transferred energy. Entropy has increased, and energy has become unavailable to do work.

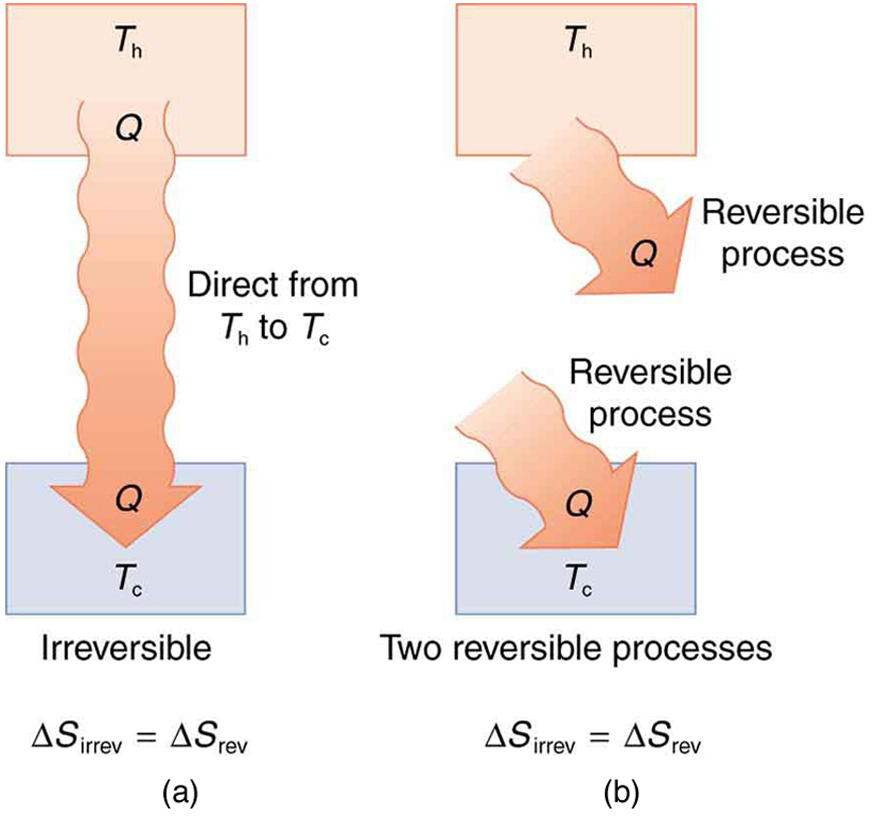
It is intuitive that entropy increases when heat flows from a hotter object to a colder one. Because entropy change is proportional to [latex]Q/T[/latex], the increase in entropy on the colder side (at lower temperature) is greater than the decrease in entropy on the hotter side. This results in a net increase in total entropy. This idea aligns with what we saw earlier and is broadly true across all physical systems:

In any real (irreversible) process, the total entropy of the system increases.

There are only two possible outcomes when considering entropy during a thermodynamic process:

• Entropy remains constant for an idealized reversible process.
• Entropy increases during a real-world irreversible process.

We can now express a fourth version of the second law of thermodynamics in terms of entropy:

The total entropy of a system and its surroundings can only increase or remain constant—it can never decrease.

For example, if heat were to transfer spontaneously from a cold object to a hot one, it would cause a decrease in total entropy, violating this version of the second law. Such a process is therefore not physically possible.

It’s important to recognize that entropy behaves very differently from energy. Energy is conserved; entropy is not. Entropy always increases in real processes. Reversible processes—like those in a theoretical Carnot engine—do not increase entropy, and are therefore the most efficient at converting heat into work. This leads us to a crucial insight:

Entropy is closely linked to the availability of energy to perform useful work.

Entropy and the Unavailability of Energy to Do Work

Why should we care about entropy in the first place? One major reason is that entropy helps explain why no real process can convert 100% of heat into useful work. An increase in entropy represents energy that becomes less organized—less usable. The next example illustrates how this increase in entropy reduces the efficiency of heat-based energy conversions.

Example 113.2 Less Work is Produced by a Given Heat Transfer When Entropy Change is Greater

(a) Calculate the work output of a Carnot engine operating between temperatures of 600 K and 100 K for 4000 J of heat transfer to the engine. (b) Now suppose that the 4000 J of heat transfer occurs first from the 600 K reservoir to a 250 K reservoir (without doing any work, and this produces the increase in entropy calculated above) before transferring into a Carnot engine operating between 250 K and 100 K. What work output is produced? (See Figure 113.4.)

Strategy

In both parts, we must first calculate the Carnot efficiency and then the work output.

Solution (a)

The Carnot efficiency is given by

[latex]{\text{Eff}}_{\text{C}}=1-\frac{{T}_{\text{c}}}{{T}_{\text{h}}}\text{.}[/latex]

Substituting the given temperatures yields

[latex]{\text{Eff}}_{\text{C}}=1-\frac{\text{100 K}}{\text{600 K}}=0\text{.}\text{833}\text{.}[/latex]

Now the work output can be calculated using the definition of efficiency for any heat engine as given by

[latex]\text{Eff}=\frac{W}{{Q}_{\text{h}}}\text{.}[/latex]

Solving for [latex]W[/latex] and substituting known terms gives

[latex]\begin{array}{lll}W& =& {\text{Eff}}_{\text{C}}{Q}_{\text{h}}\\ & =& \left(0.833\right)\left(\text{4000}\phantom{\rule{0.25em}{0ex}}\text{J}\right)=\text{3333 J.}\end{array}[/latex]

Solution (b)

Similarly,

[latex]{\text{Eff}\prime }_{\text{C}}=1-\frac{{T}_{\text{c}}}{{\text{T′}}_{\text{c}}}=\text{1}-\frac{\text{100 K}}{\text{250 K}}=0.600,[/latex]

so that

[latex]\begin{array}{lll}W& =& {\text{Eff}\prime }_{\text{C}}{Q}_{h}\\ & =& \left(0.600\right)\left(\text{4000 J}\right)=\text{2400 J.}\end{array}[/latex]

Discussion

There is 933 J less work from the same heat transfer in the second process. This result is important. The same heat transfer into two perfect engines produces different work outputs, because the entropy change differs in the two cases. In the second case, entropy is greater and less work is produced. Entropy is associated with the unavailability of energy to do work.

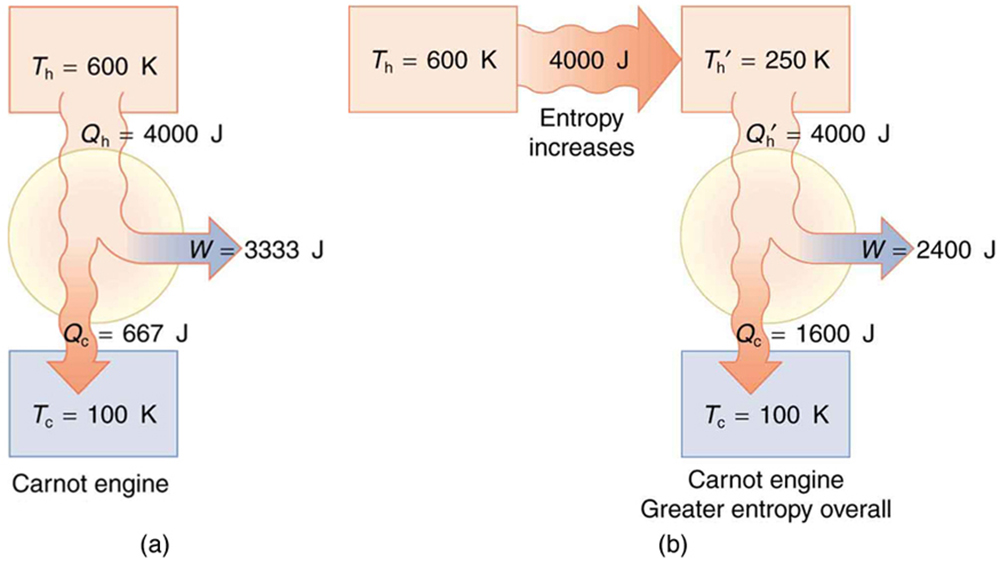
When entropy increases, a portion of energy becomes permanently unavailable to do useful work. This energy isn’t destroyed—total energy is still conserved—but it becomes so disordered that it can no longer be harnessed to perform organized tasks, such as moving a piston or powering a turbine. This unavailable energy represents the lost potential for doing work due to increasing disorder.

For example, in the scenario we considered earlier, a [latex]4000 \ \text{J}[/latex] heat transfer from a [latex]600 \ \text{K}[/latex] reservoir to a [latex]250 \ \text{K}[/latex] reservoir resulted in an entropy increase of [latex]9.33 \ \text{J/K}[/latex]. The amount of energy that became unavailable for work is calculated using the formula:

Here, [latex]T_0[/latex] is the temperature of the coldest reservoir involved (in this case, [latex]100 \ \text{K}[/latex]). Substituting in the values gives:

This 933 J is the portion of energy that cannot be used for work due to the entropy increase.

Heat Death of the Universe: An Overdose of Entropy

In the early universe, matter and energy were densely packed and highly uniform. There were few temperature differences, and everything was in an extremely energetic state. However, as the universe expanded and cooled, entropy began to increase and distinct structures formed—stars, planets, and galaxies.

These temperature differences between hot stars and cooler planets created the potential for work—driving winds, powering ecosystems, and fueling engines. Over time, however, these sources of usable energy are being depleted. Stars will eventually burn through their nuclear fuel, planets will cool, and temperature differences will diminish.

Even here on Earth, we rely on energy sources like fossil fuels, nuclear power, geothermal heat, solar radiation, and tidal forces. But as we use these resources, a portion of the energy becomes disordered and unusable. The entropy of the Earth—and of the entire universe—is always increasing.

The Earth is not an isolated system; energy from the Sun replenishes our usable energy stores. Thanks to the Sun, we continue to have wind, photosynthesis, liquid water, and a stable climate. But the Sun itself has a finite lifespan—approximately five billion more years—and once it exhausts its fuel, Earth’s ability to support work-driven processes will eventually fade.

In the long term, as entropy continues to increase throughout the universe, all usable energy will be transformed into a state of uniform disorder. When that happens, no more work will be possible. No engines, no life, no motion. This ultimate state of equilibrium is called the heat death of the universe. Whether the universe ends in a cold, dark expansion or a fiery contraction, its entropy will reach a maximum, and no further energy transformations will be possible.

Despite how ominous this sounds, the end is not near. Some calculations suggest that the universe could continue evolving for at least [latex]10^{100}[/latex] years—a time scale vastly longer than the age of our current cosmos.

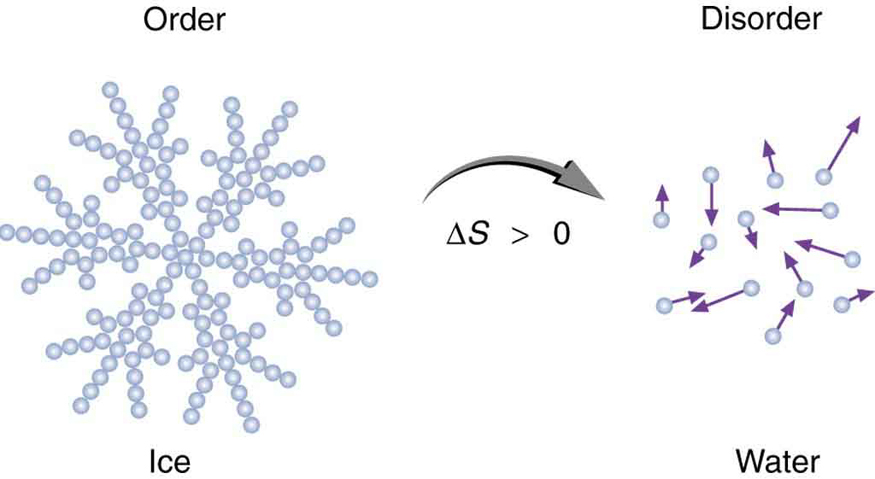
Order to Disorder

Entropy is not only about energy—it also provides a powerful way to measure disorder in a system. This concept, first proposed by physicist Ludwig Boltzmann, helps explain everyday phenomena. For instance, when an ice cube melts, its water molecules go from being tightly arranged in a crystalline structure to moving freely in a liquid. This transition represents a significant increase in disorder—and therefore, a significant increase in entropy.

We’ll explore this idea further in the next example, where the melting of ice is analyzed in terms of entropy change. See Figure 113.5 for a visual comparison of order and disorder during phase transitions.

Example 113.3: Entropy Associated with Disorder

Find the increase in entropy of 1.00 kg of ice originally at [latex]0º C[/latex] that is melted to form water at [latex]0º C[/latex].

Strategy

As before, the change in entropy can be calculated from the definition of [latex]\Delta S[/latex] once we find the energy [latex]Q[/latex] needed to melt the ice.

Solution

The change in entropy is defined as:

[latex]\mathrm{\Delta S}=\frac{Q}{T}\text{.}[/latex]

Here [latex]Q[/latex] is the heat transfer necessary to melt 1.00 kg of ice and is given by

[latex]Q={\text{mL}}_{\text{f}\text{,}}[/latex]

where [latex]m[/latex] is the mass and [latex]{L}_{\text{f}}[/latex] is the latent heat of fusion. [latex]{L}_{\text{f}}=\text{334}\phantom{\rule{0.25em}{0ex}}\text{kJ/kg}[/latex] for water, so that

[latex]Q=\left(1.00 kg\right)\left(334 kJ/kg\right)=3\text{.}\text{34}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{J.}[/latex]

Now the change in entropy is positive, since heat transfer occurs into the ice to cause the phase change; thus,

[latex]\Delta S=\frac{Q}{T}=\frac{3\text{.}\text{34}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{J}}{T}\text{.}[/latex]

[latex]T[/latex] is the melting temperature of ice. That is, [latex]T=0º\text{C=273 K}[/latex]. So the change in entropy is

[latex]\begin{array}{lll}\Delta S& =& \frac{3\text{.}\text{34}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{J}}{\text{273 K}}\\ & =& \text{1.22}×{\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}\text{J/K.}\end{array}[/latex]

Discussion

This is a significant increase in entropy accompanying an increase in disorder.

Let’s consider another relatable example. Suppose you mix equal masses of water at two different temperatures—say, one at [latex]20.0^\circ \text{C}[/latex] and the other at [latex]40.0^\circ \text{C}[/latex]. The result will be water at a uniform intermediate temperature of [latex]30.0^\circ \text{C}[/latex]. This seemingly simple action has several important thermodynamic consequences:

• Entropy increases: Just as with any irreversible heat transfer, the entropy of the hot water decreases, but the cold water’s entropy increases by a greater amount. The total entropy of the system increases.
• Energy becomes unavailable: Once the system reaches equilibrium at a uniform temperature, no more useful work can be extracted using a heat engine. The potential to do work has been lost.
• Increased disorder: The system becomes more disordered. Instead of two distinct thermal reservoirs, we now have one uniform system with less structural or thermal differentiation.

These outcomes—greater entropy, reduced work potential, and increased disorder—are fundamentally connected. In fact, they are different ways of describing the same thermodynamic phenomenon.

Life, Evolution, and the Second Law of Thermodynamics

Some critics mistakenly claim that biological evolution contradicts the second law of thermodynamics, arguing that increasing complexity in life represents a decrease in entropy. However, this argument overlooks a key point: the second law applies to closed systems. Earth is not a closed system—it constantly receives energy from the Sun.

The second law of thermodynamics, when stated in terms of entropy, says that:

[latex]\Delta S_{\text{tot}} = \Delta S_{\text{syst}} + \Delta S_{\text{envir}} > 0[/latex]

This means that while the entropy of a system ([latex]\Delta S_{\text{syst}}[/latex]) can decrease, it must be offset by a greater increase in the entropy of the environment ([latex]\Delta S_{\text{envir}}[/latex]).

How does this apply to life and evolution? Every time a living organism grows, or complex molecules are synthesized from simpler ones, local entropy decreases. But that decrease is fueled by energy input—whether from chemical energy, geothermal sources, or most importantly, from sunlight. This energy transfer increases entropy elsewhere in the universe, more than offsetting the local decrease in entropy.

Think of it this way: when a plant stores solar energy through photosynthesis, it’s creating an organized structure with lower entropy. But the Sun emits vast amounts of thermal radiation into cold outer space during that same process. The net effect is a large increase in universal entropy, even though local structures on Earth are becoming more complex and ordered.

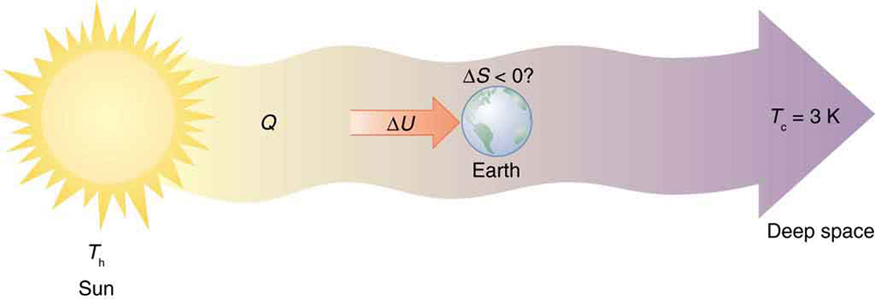
In this way, Earth functions as a kind of heat engine. It absorbs energy from the Sun (a high-temperature reservoir) and radiates waste heat into outer space (a low-temperature reservoir at about 3 K). During this transfer, life emerges and evolves as a form of ordered structure—but without violating the second law.

As shown in Figure 113.6, Earth is just a small node in a much larger thermodynamic system. The entropy of the entire process—Sun to space—still increases, even if entropy on Earth locally decreases.