Dynamics: Force and Newton’s Laws of Motion and Applications: Friction, Drag and Elasticity
32 Elasticity: Stress and Strain
Learning Objectives
- State Hooke’s law.
- Explain Hooke’s law using graphical representation between deformation and applied force.
- Discuss the three types of deformations such as changes in length, sideways shear and changes in volume.
- Describe with examples the young’s modulus, shear modulus and bulk modulus.
- Determine the change in length given mass, length and radius.
Elastic Deformations in Biological Systems
We now shift focus from how forces affect motion to how forces deform objects. For example, when a muscle pulls on a tendon, it stretches. When a person stands, their bones compress slightly. These shape changes—called deformations—are the focus of this chapter.
For small deformations, two key characteristics emerge:
-
The object returns to its original shape when the force is removed (elastic behavior).
-
The deformation is proportional to the applied force—this is Hooke’s Law.
In equation form:
[latex]F = k\Delta L[/latex]
-
[latex]F[/latex] is the applied force.
-
[latex]\Delta L[/latex] is the change in length.
-
[latex]k[/latex] is a constant depending on material and geometry.
Rearranged:
[latex]\Delta L = \frac{F}{k}[/latex]
This shows deformation is directly proportional to the force.
Figure 32.1 illustrates a typical deformation vs. force graph. The straight region is where Hooke’s Law holds. Beyond this, deformation becomes nonlinear and eventually leads to fracture.
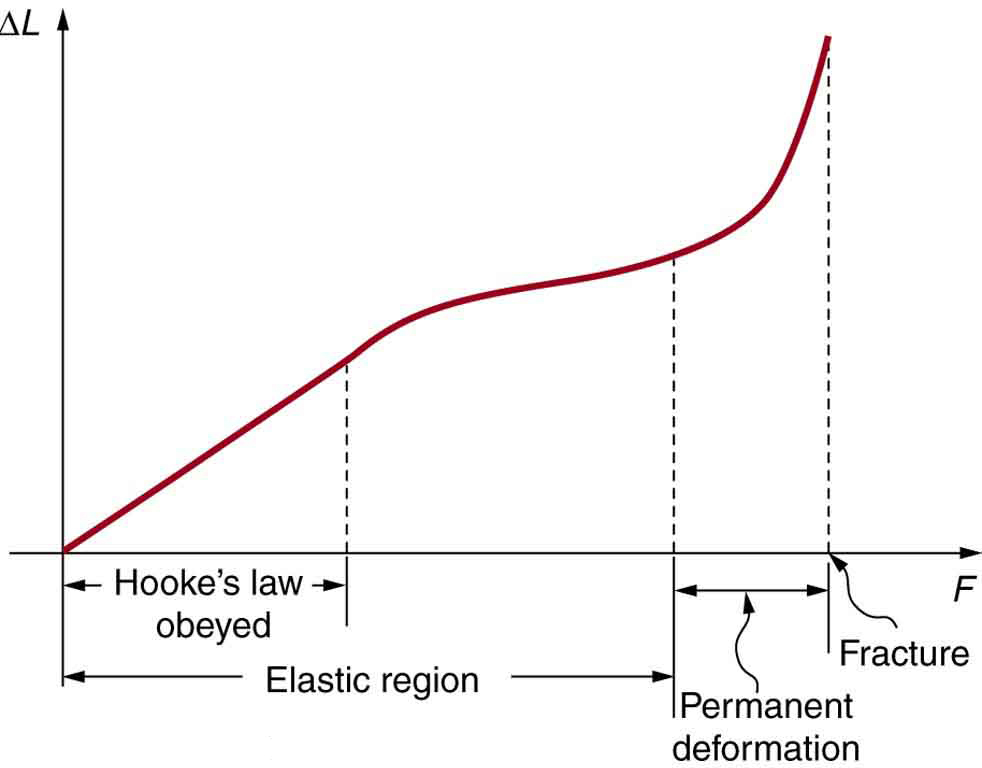
Biological Example: Tendons, Bones, and Elastic Limits
Tendons connect muscle to bone and must stretch when force is applied but return to their original length—perfect candidates for Hookean behavior. Bones also deform, but much less so, and tend to fracture if stressed beyond the elastic region.
Dependence on Material and Geometry
The proportionality constant [latex]k[/latex] (see Figure 32.2) depends on:
-
the material’s intrinsic stiffness
-
the cross-sectional area
-
the original length
We combine these into:
[latex]\Delta L = \frac{1}{Y}\frac{F}{A}L_0[/latex]
-
[latex]Y[/latex] is Young’s modulus, a measure of stiffness.
-
[latex]A[/latex] is the cross-sectional area.
-
[latex]L_0[/latex] is the original length.
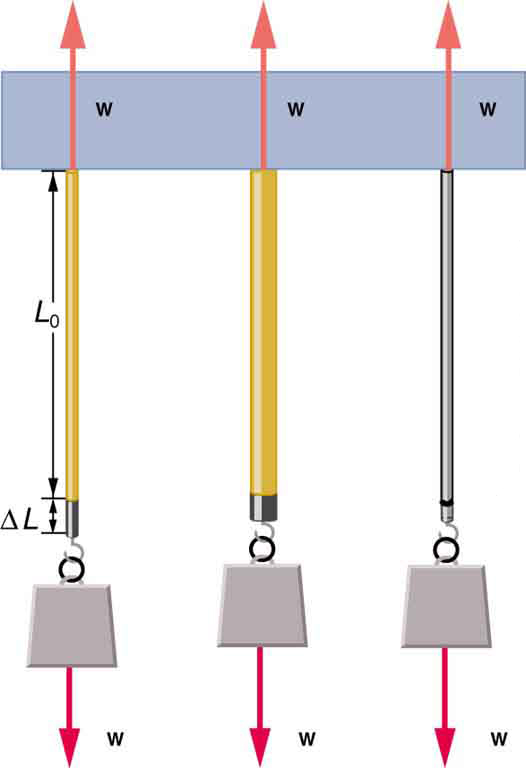
Stretch Yourself a Little
How would you go about measuring the proportionality constant [latex]k[/latex] of a rubber band? If a rubber band stretched 3 cm when a 100-g mass was attached to it, then how much would it stretch if two similar rubber bands were attached to the same mass—even if put together in parallel or alternatively if tied together in series?
We now consider three specific types of deformations: changes in length (tension and compression), sideways shear (stress), and changes in volume. All deformations are assumed to be small unless otherwise stated.
Changes in Length—Tension and Compression: Elastic Modulus
A change in length [latex]\Delta L[/latex] is produced when a force is applied to a wire or rod parallel to its length [latex]{L}_{0}[/latex], either stretching it (a tension) or compressing it. (See Figure 32.3.)
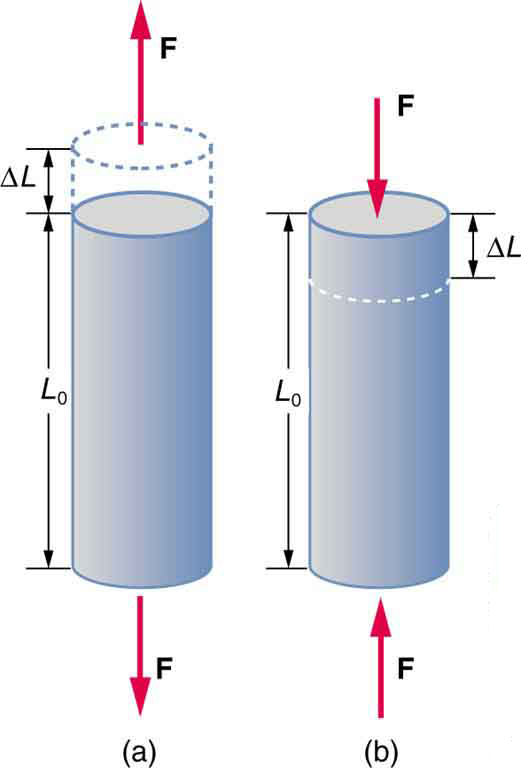
Experiments have shown that the change in length ([latex]\Delta L[/latex]) depends on only a few variables. As already noted, [latex]\Delta L[/latex] is proportional to the force [latex]F[/latex] and depends on the substance from which the object is made. Additionally, the change in length is proportional to the original length [latex]{L}_{0}[/latex] and inversely proportional to the cross-sectional area of the wire or rod. For example, a long guitar string will stretch more than a short one, and a thick string will stretch less than a thin one. We can combine all these factors into one equation for [latex]\Delta L[/latex]:
where [latex]\Delta L[/latex] is the change in length, [latex]F[/latex] the applied force, [latex]Y[/latex] is a factor, called the elastic modulus or Young’s modulus, that depends on the substance, [latex]A[/latex] is the cross-sectional area, and [latex]{L}_{0}[/latex] is the original length. Table 32.1 lists values of [latex]Y[/latex] for several materials—those with a large [latex]Y[/latex] are said to have a large tensile stiffness because they deform less for a given tension or compression.
| Material | Young’s modulus (tension–compression)Y [latex]\left({\text{10}}^{\text{9}}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{\text{2}}\right)[/latex] | Shear modulus S[latex]\left({\text{10}}^{\text{9}}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{\text{2}}\right)[/latex] | Bulk modulus B [latex]\left({\text{10}}^{\text{9}}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{\text{2}}\right)[/latex] |
|---|---|---|---|
| Aluminum | 70 | 25 | 75 |
| Bone – tension | 16 | 80 | 8 |
| Bone – compression | 9 | ||
| Brass | 90 | 35 | 75 |
| Brick | 15 | ||
| Concrete | 20 | ||
| Glass | 70 | 20 | 30 |
| Granite | 45 | 20 | 45 |
| Hair (human) | 10 | ||
| Hardwood | 15 | 10 | |
| Iron, cast | 100 | 40 | 90 |
| Lead | 16 | 5 | 50 |
| Marble | 60 | 20 | 70 |
| Nylon | 5 | ||
| Polystyrene | 3 | ||
| Silk | 6 | ||
| Spider thread | 3 | ||
| Steel | 210 | 80 | 130 |
| Tendon | 1 | ||
| Acetone | 0.7 | ||
| Ethanol | 0.9 | ||
| Glycerin | 4.5 | ||
| Mercury | 25 | ||
| Water | 2.2 |
Young’s moduli are not listed for liquids and gases in Table 32.1 because they cannot be stretched or compressed in only one direction. Note that there is an assumption that the object does not accelerate, so that there are actually two applied forces of magnitude [latex]F[/latex] acting in opposite directions. For example, the strings in Figure 32.3 are being pulled down by a force of magnitude [latex]w[/latex] and held up by the ceiling, which also exerts a force of magnitude [latex]w[/latex].
Example 32.1: The Stretch of a Long Cable
Suspension cables are used to carry gondolas at ski resorts. (See Figure 32.4) Consider a suspension cable that includes an unsupported span of 3 km. Calculate the amount of stretch in the steel cable. Assume that the cable has a diameter of 5.6 cm and the maximum tension it can withstand is [latex]3\text{.}0×{\text{10}}^{6}\phantom{\rule{0.25em}{0ex}}\text{N}[/latex].

Strategy
The force is equal to the maximum tension, or [latex]F=3\text{.}0×{\text{10}}^{6}\phantom{\rule{0.25em}{0ex}}\text{N}[/latex]. The cross-sectional area is [latex]{\mathrm{\pi r}}^{2}=2\text{.}\text{46}×{\text{10}}^{-3}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{2}[/latex]. The equation [latex]\Delta L=\frac{1}{Y}\frac{F}{A}{L}_{0}[/latex] can be used to find the change in length.
Solution
All quantities are known. Thus,
Discussion
This is quite a stretch, but only about 0.6% of the unsupported length. Effects of temperature upon length might be important in these environments.
Biological Applications of Elasticity
Bones Under Load
Bones, while strong under tension and compression, are more likely to fracture under shear or bending forces. When a sideways impact or torsional stress occurs—like during a fall—the bone can snap or shear, rather than compress. Bones serve as weight-bearing columns, like those found in architecture or tree trunks. They are reinforced naturally with fibrous structures, just as buildings use steel rods.
The internal architecture of bones varies depending on their location and function. For instance:
-
Femur head: Made of thin, sheet-like bone separated by marrow to manage compressive stress.
-
Long bones (e.g., tibia, humerus): Cylindrical, solid or marrow-filled, optimized for longitudinal stress.
-
Joint bones: Especially sensitive to sustained compression, which is why overweight individuals are prone to joint and tendon damage.
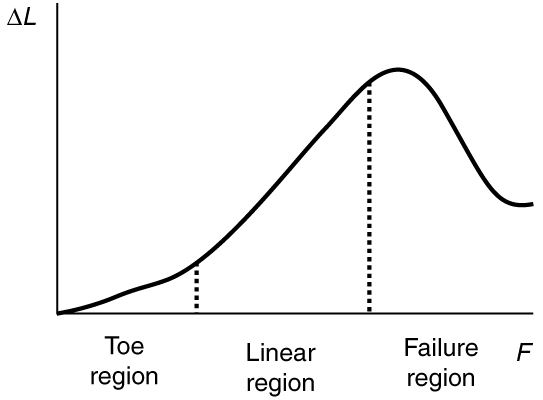
Tendons: Nonlinear Elasticity
Tendons connect muscle to bone and exhibit nonlinear elasticity—a hallmark of complex biological materials. This means that tendons:
-
Stretch easily at first (low stiffness in the toe region).
-
Become significantly stiffer under larger forces (in the linear region).
-
Eventually fail if the force continues (in the failure region).
Figure 32.5 shows the stress-strain curve for mammalian tendon:
This behavior is often modeled by parallel springs, where each spring activates at different lengths of stretch—mimicking how different collagen fibers respond.
Ligaments, Arteries, Lungs, and Skin
-
Ligaments (connecting bone to bone) behave similarly to tendons, though often with lower strain tolerance.
-
Arteries must be highly elastic to accommodate blood pressure pulses. When blood is pumped out of the heart, the arterial walls expand. When the aortic valve closes, elastic recoil helps maintain blood flow.
-
Lungs expand with muscular effort and recoil passively—another beautiful example of elasticity in function.
-
Skin, especially in young individuals, exhibits remarkable elasticity. Youthful skin can accommodate large body size changes (e.g., pregnancy, weight loss) with little sag.
-
Unfortunately, elasticity diminishes with age, beginning subtly in our 20s. This affects not just cosmetic properties, but also organ function.
Example 32.2: Calculating Deformation: How Much Does Your Leg Shorten When You Stand on It?
Calculate the change in length of the upper leg bone (the femur) when a 70.0 kg man supports 62.0 kg of his mass on it, assuming the bone to be equivalent to a uniform rod that is 40.0 cm long and 2.00 cm in radius.
Strategy
The force is equal to the weight supported, or
and the cross-sectional area is [latex]{\mathrm{\pi r}}^{2}=1\text{.}\text{257}×{\text{10}}^{-3}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{2}[/latex]. The equation [latex]\Delta L=\frac{1}{Y}\frac{F}{A}{L}_{0}[/latex] can be used to find the change in length.
Solution
All quantities except [latex]\Delta L[/latex] are known. Note that the compression value for Young’s modulus for bone must be used here. Thus,
Discussion
This small change in length seems reasonable, consistent with our experience that bones are rigid. In fact, even the rather large forces encountered during strenuous physical activity do not compress or bend bones by large amounts. Although bone is rigid compared with fat or muscle, several of the substances listed in Table 32.1 have larger values of Young’s modulus [latex]Y[/latex]. In other words, they are more rigid.
Stress, Strain, and Shear: Extensions of Hooke’s Law
The equation for change in length due to an applied force can be rearranged and written as:
[latex]\frac{F}{A} = Y \frac{\Delta L}{L_0},[/latex]
where:
-
[latex]\frac{F}{A}[/latex] is the stress (in [latex]\text{N/m}^2[/latex]),
-
[latex]\frac{\Delta L}{L_0}[/latex] is the strain (dimensionless), and
-
[latex]Y[/latex] is Young’s modulus (a material-specific constant).
In other words,
[latex]\text{stress} = Y \times \text{strain}.[/latex]
This form mirrors Hooke’s law, treating stress like force and strain like deformation. If we solve for force, we get:
[latex]F = Y A \frac{\Delta L}{L_0},[/latex]
and the proportionality constant resembles a spring constant:
[latex]k = \frac{YA}{L_0}.[/latex]
This general idea—that force and the deformation it causes are proportional for small deformations—applies to changes in length, sideways bending, and changes in volume.
Definitions
Stress
The ratio of force to area:
[latex]\text{stress} = \frac{F}{A}[/latex]
Units: [latex]\text{N/m}^2[/latex]
Strain
The ratio of change in length to the original length:
[latex]\text{strain} = \frac{\Delta L}{L_0}[/latex]
(Strain has no units.)
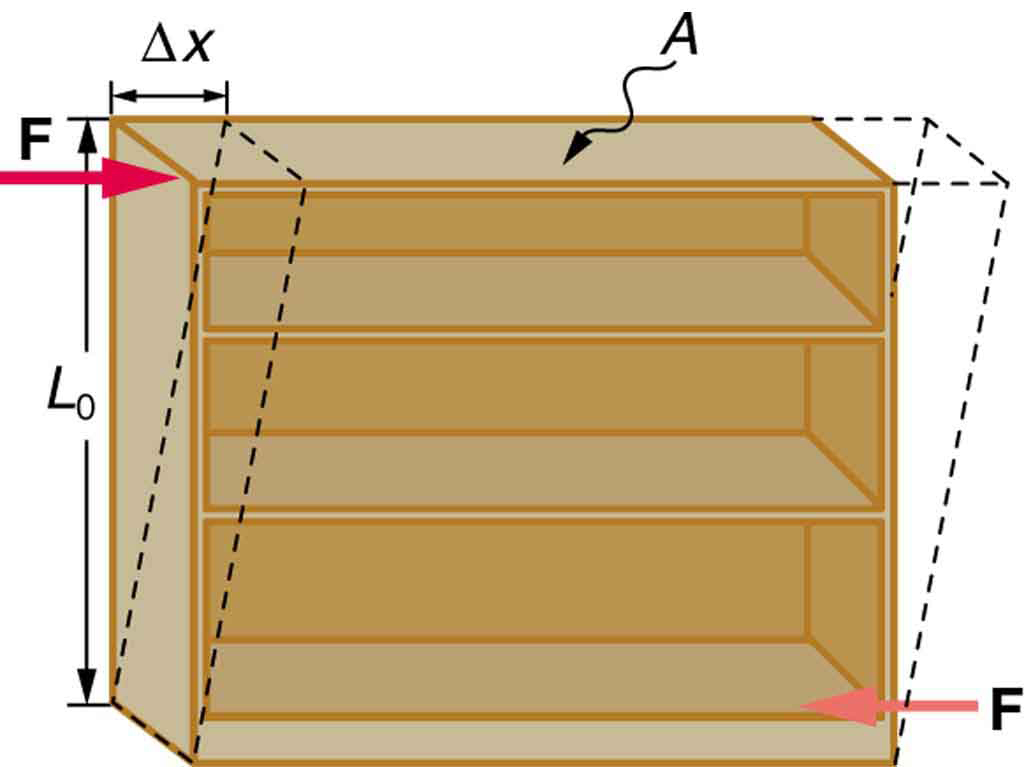
Sideways Stress: Shear Modulus
Sideways stress, or shear, is another important deformation mode. In this case, the deformation [latex]\Delta x[/latex] is perpendicular to the original length [latex]L_0[/latex]. This behavior follows a similar relation:
[latex]\Delta x = \frac{1}{S} \frac{F}{A} L_0,[/latex]
where:
-
[latex]S[/latex] is the shear modulus,
-
[latex]F[/latex] is the force applied parallel to the surface, and
-
[latex]A[/latex] is the cross-sectional area across which the force is applied.
Shear Deformation
[latex]\Delta x = \frac{1}{S} \frac{F}{A} L_0[/latex]
As illustrated in Figure 32.6, two equal and opposite shearing forces [latex]F[/latex] are applied, and the object deforms by [latex]\Delta x[/latex] without rotating.
Shearing is easier in objects with longer lengths, smaller cross-sectional areas, or lower shear modulus—like rubber or soft tissues.
Biological Implications of Shear Stress
-
Bone is a surprising case: its shear modulus exceeds its Young’s modulus and approaches that of steel, which explains its rigidity.
-
The spinal column, comprised of 26 vertebrae separated by discs, is highly affected by shear forces—especially at its curved lower end.
-
Pregnancy or obesity increases curvature, hence increasing shear on the lumbosacral disc, which raises risk for disc rupture.
-
-
Concrete and brick have very low shear moduli and resist compression far better than shear. This is why steel reinforcement is critical in modern buildings.
-
Liquids and gases flow under shear and are considered to have zero shear modulus.
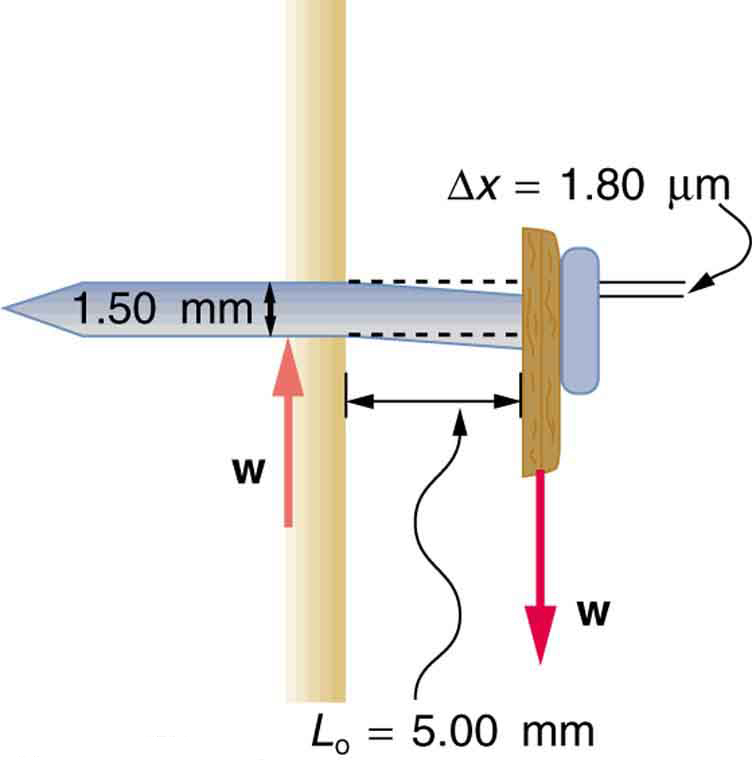
Example 32.3:Calculating Force Required to Deform: That Nail Does Not Bend Much Under a Load
Find the mass of the picture hanging from a steel nail as shown in Figure 32.7, given that the nail bends only [latex]\text{1.80 µm}[/latex]. (Assume the shear modulus is known to two significant figures.)
Strategy
The force [latex]F[/latex] on the nail (neglecting the nail’s own weight) is the weight of the picture [latex]w[/latex]. If we can find [latex]w[/latex], then the mass of the picture is just [latex]\frac{w}{g}[/latex] . The equation [latex]\Delta x=\frac{1}{S}\frac{F}{A}{L}_{0}[/latex] can be solved for [latex]F[/latex].
Solution
Solving the equation [latex]\Delta x=\frac{1}{S}\frac{F}{A}{L}_{0}[/latex] for [latex]F[/latex], we see that all other quantities can be found:
S is found in Table 32.1 and is [latex]S=\text{80}×{\text{10}}^{9}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}[/latex]. The radius [latex]r[/latex] is 0.750 mm (as seen in the figure), so the cross-sectional area is
The value for [latex]{L}_{0}[/latex] is also shown in the figure. Thus,
This 51 N force is the weight [latex]w[/latex] of the picture, so the picture’s mass is
Discussion
This is a fairly massive picture, and it is impressive that the nail flexes only
[latex]\text{1.80 µm}[/latex]—an amount undetectable to the unaided eye.
Changes in Volume: Bulk Modulus
An object will be compressed in all directions if inward forces are applied evenly across all its surfaces, as shown in Figure 32.8. Gases are relatively easy to compress, whereas liquids and solids are extremely difficult to compress. For example, the air in a wine bottle is compressed when corked, but a brim-full bottle of wine cannot be corked unless some liquid is removed—liquids are nearly incompressible.
The reason lies in the structure of matter: gases have atoms and molecules widely spaced, allowing them to be pushed closer together. In contrast, atoms and molecules in liquids and solids are already tightly packed, and further compression means pushing against strong electromagnetic forces between them.
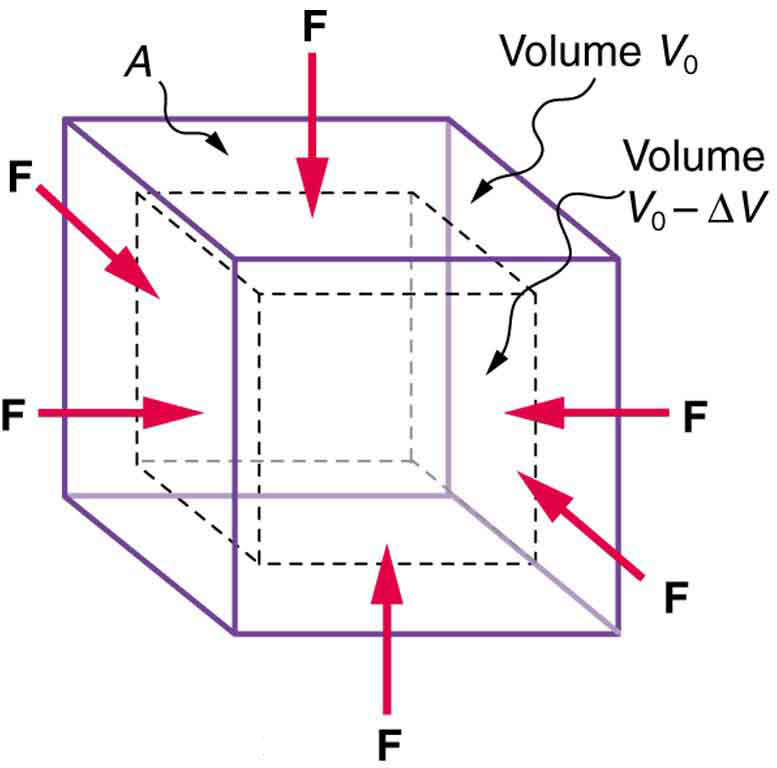
Bulk Modulus Equation
A uniformly applied inward force generates the same stress, defined as force per unit area [latex]\frac{F}{A}[/latex], on all surfaces of an object. This results in a change in volume, [latex]\Delta V[/latex], given by:
[latex]\Delta V = \frac{1}{B} \frac{F}{A} V_0,[/latex]
where:
-
[latex]B[/latex] is the bulk modulus (see Table 32.1),
-
[latex]V_0[/latex] is the original volume,
-
[latex]\frac{F}{A}[/latex] is the inward pressure applied uniformly on all sides.
This expression, like those for shear and tension, shows how deformation (in this case, volume change) depends on both the applied stress and the material’s resistance.
Note: Bulk modulus is typically not defined for gases, since they compress too easily to follow the same relationship.
Real-World Applications of Bulk Modulus
-
Industrial diamonds are created by applying massive pressure to carbon. The atoms are forced into a tightly packed crystal structure, forming diamond.
-
Natural diamond formation occurs under similar conditions, deep beneath Earth’s surface where overlying rock exerts extreme compressive forces.
-
Deep-sea pressure is another example. Water pressure increases with depth and exerts inward forces on submerged objects—and even on the water itself. At sufficient depths, water itself becomes measurably compressed.
Example 32.4: Calculating Change in Volume with Deformation: How Much Is Water Compressed at Great Ocean Depths?
Calculate the fractional decrease in volume ([latex]\frac{\Delta V}{{V}_{0}}[/latex]) for seawater at 5.00 km depth, where the force per unit area is [latex]5\text{.}\text{00}×{\text{10}}^{7}\phantom{\rule{0.25em}{0ex}}N/{m}^{2}[/latex].
Strategy
Equation [latex]\Delta V=\frac{1}{B}\frac{F}{A}{V}_{0}[/latex] is the correct physical relationship. All quantities in the equation except [latex]\frac{\Delta V}{{V}_{0}}[/latex]
are known.
Solution
Solving for the unknown
gives
Substituting known values with the value for the bulk modulus [latex]B[/latex] from Table 32.1,
Discussion
Although measurable, this is not a significant decrease in volume considering that the force per unit area is about 500 atmospheres (1 million pounds per square foot). Liquids and solids are extraordinarily difficult to compress.
Conversely, very large internal forces are generated when liquids or solids attempt to expand but are constrained from doing so. This situation is mechanically equivalent to compressing them below their equilibrium volume. Such conditions frequently arise due to thermal expansion: most materials increase in volume as their temperature rises. When this expansion is restricted, the resulting internal stresses can cause significant deformation or even failure of the surrounding container.
A dramatic and common illustration of this occurs when water freezes. Unlike most substances, water expands upon freezing. This expansion can exert enough force to:
-
Fracture rocks and boulders through freeze-thaw weathering,
-
Rupture biological cells, causing frost damage in plants and tissues,
-
Crack engine blocks or pipes if water inside them freezes without space to expand.
These phenomena emphasize the importance of understanding elastic and plastic deformation across materials under varying physical conditions.
Finally, it is worth noting that other types of deformation—such as torsion (twisting)—follow similar mechanical principles as those described for tension, shear, and bulk compression. These torsional deformations are characterized by their own modulus (the torsion modulus) and will be encountered in further sections or advanced studies.
Section Summary
-
Hooke’s Law describes the linear relationship between force and deformation for small deformations:
[latex]F = k,\Delta L,[/latex]
where:-
[latex]F[/latex] is the applied force,
-
[latex]\Delta L[/latex] is the change in length,
-
[latex]k[/latex] is the stiffness (spring constant), dependent on the object’s geometry and material.
-
-
For uniform materials, this relationship becomes:
[latex]\Delta L = \frac{1}{Y}\frac{F}{A}L_0,[/latex]
where:-
[latex]Y[/latex] is Young’s modulus (tensile stiffness),
-
[latex]A[/latex] is the cross-sectional area,
-
[latex]L_0[/latex] is the original length.
-
-
Stress is the force per unit area:
[latex]\text{stress} = \frac{F}{A} \quad (\text{in } \text{N/m}^2),[/latex]
-
Strain is the relative deformation:
[latex]\text{strain} = \frac{\Delta L}{L_0} \quad (\text{unitless}),[/latex]
-
Combining both gives:
[latex]\text{stress} = Y \times \text{strain}.[/latex]
-
Shear deformation describes sideways distortion:
[latex]\Delta x = \frac{1}{S} \frac{F}{A} L_0,[/latex]
where:-
[latex]S[/latex] is the shear modulus,
-
[latex]F[/latex] is the force applied parallel to the surface area [latex]A[/latex],
-
[latex]L_0[/latex] is the height or length across which shear occurs.
-
-
Bulk deformation (compression of volume) is described by:
[latex]\Delta V = \frac{1}{B} \frac{F}{A} V_0,[/latex]
where:-
[latex]B[/latex] is the bulk modulus,
-
[latex]V_0[/latex] is the original volume,
-
[latex]\frac{F}{A}[/latex] is the inward force per unit area applied uniformly.
-
Conceptual Questions
- The elastic properties of the arteries are essential for blood flow. Explain the importance of this in terms of the characteristics of the flow of blood (pulsating or continuous).
- What are you feeling when you feel your pulse? Measure your pulse rate for 10 s and for 1 min. Is there a factor of 6 difference?
- Examine different types of shoes, including sports shoes and thongs. In terms of physics, why are the bottom surfaces designed as they are? What differences will dry and wet conditions make for these surfaces?
- Would you expect your height to be different depending upon the time of day? Why or why not?
- Why can a squirrel jump from a tree branch to the ground and run away undamaged, while a human could break a bone in such a fall?
- Explain why pregnant women often suffer from back strain late in their pregnancy.
- An old carpenter’s trick to keep nails from bending when they are pounded into hard materials is to grip the center of the nail firmly with pliers. Why does this help?
- When a glass bottle full of vinegar warms up, both the vinegar and the glass expand, but vinegar expands significantly more with temperature than glass. The bottle will break if it was filled to its tightly capped lid. Explain why, and also explain how a pocket of air above the vinegar would prevent the break. (This is the function of the air above liquids in glass containers.)
Problems & Exercises
- During a circus act, one performer swings upside down hanging from a trapeze holding another, also upside-down, performer by the legs. If the upward force on the lower performer is three times her weight, how much do the bones (the femurs) in her upper legs stretch? You may assume each is equivalent to a uniform rod 35.0 cm long and 1.80 cm in radius. Her mass is 60.0 kg.
- During a wrestling match, a 150 kg wrestler briefly stands on one hand during a maneuver designed to perplex his already moribund adversary. By how much does the upper arm bone shorten in length? The bone can be represented by a uniform rod 38.0 cm in length and 2.10 cm in radius.
- (a) The “lead” in pencils is a graphite composition with a Young’s modulus of about [latex]1×{\text{10}}^{9}\phantom{\rule{0.25em}{0ex}}\text{N}/{\text{m}}^{2}[/latex]. Calculate the change in length of the lead in an automatic pencil if you tap it straight into the pencil with a force of 4.0 N. The lead is 0.50 mm in diameter and 60 mm long. (b) Is the answer reasonable? That is, does it seem to be consistent with what you have observed when using pencils?
- TV broadcast antennas are the tallest artificial structures on Earth. In 1987, a 72.0-kg physicist placed himself and 400 kg of equipment at the top of one 610-m high antenna to perform gravity experiments. By how much was the antenna compressed, if we consider it to be equivalent to a steel cylinder 0.150 m in radius?
- (a) By how much does a 65.0-kg mountain climber stretch her 0.800-cm diameter nylon rope when she hangs 35.0 m below a rock outcropping? (b) Does the answer seem to be consistent with what you have observed for nylon ropes? Would it make sense if the rope were actually a bungee cord?
- A 20.0-m tall hollow aluminum flagpole is equivalent in stiffness to a solid cylinder 4.00 cm in diameter. A strong wind bends the pole much as a horizontal force of 900 N exerted at the top would. How far to the side does the top of the pole flex?
- As an oil well is drilled, each new section of drill pipe supports its own weight and that of the pipe and drill bit beneath it. Calculate the stretch in a new 6.00 m length of steel pipe that supports 3.00 km of pipe having a mass of 20.0 kg/m and a 100-kg drill bit. The pipe is equivalent in stiffness to a solid cylinder 5.00 cm in diameter.
- Calculate the force a piano tuner applies to stretch a steel piano wire 8.00 mm, if the wire is originally 0.850 mm in diameter and 1.35 m long.
- A vertebra is subjected to a shearing force of 500 N. Find the shear deformation, taking the vertebra to be a cylinder 3.00 cm high and 4.00 cm in diameter. [latex]1\text{.}\text{49}×{\text{10}}^{-7}\phantom{\rule{0.25em}{0ex}}\text{m}[/latex]
- A disk between vertebrae in the spine is subjected to a shearing force of 600 N. Find its shear deformation, taking it to have the shear modulus of [latex]1×{\text{10}}^{9}\phantom{\rule{0.25em}{0ex}}\text{N}/{\text{m}}^{2}[/latex]. The disk is equivalent to a solid cylinder 0.700 cm high and 4.00 cm in diameter.
- When using a pencil eraser, you exert a vertical force of 6.00 N at a distance of 2.00 cm from the hardwood-eraser joint. The pencil is 6.00 mm in diameter and is held at an angle of [latex]\text{20.0º}[/latex] to the horizontal. (a) By how much does the wood flex perpendicular to its length? (b) How much is it compressed lengthwise?
- To consider the effect of wires hung on poles, we take data from Problem Solving Strategies Example 2, in which tensions in wires supporting a traffic light were calculated. The left wire made an angle [latex]\text{30.0º}[/latex] below the horizontal with the top of its pole and carried a tension of 108 N. The 12.0 m tall hollow aluminum pole is equivalent in stiffness to a 4.50 cm diameter solid cylinder. (a) How far is it bent to the side? (b) By how much is it compressed?
- A farmer making grape juice fills a glass bottle to the brim and caps it tightly. The juice expands more than the glass when it warms up, in such a way that the volume increases by 0.2% (that is, [latex]\Delta V/{V}_{0}=2×{\text{10}}^{-3}[/latex]) relative to the space available. Calculate the magnitude of the normal force exerted by the juice per square centimeter if its bulk modulus is [latex]1\text{.}8×{\text{10}}^{9}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}[/latex], assuming the bottle does not break. In view of your answer, do you think the bottle will survive.
- (a) When water freezes, its volume increases by 9.05% (that is,
[latex]\frac{\Delta V}{V_0} = 9.05 \times 10^{-2}[/latex]
What force per unit area is water capable of exerting on a container when it freezes? (It is acceptable to use the bulk modulus of water in this problem.)
(b) Is it surprising that such forces can fracture engine blocks, boulders, and the like?
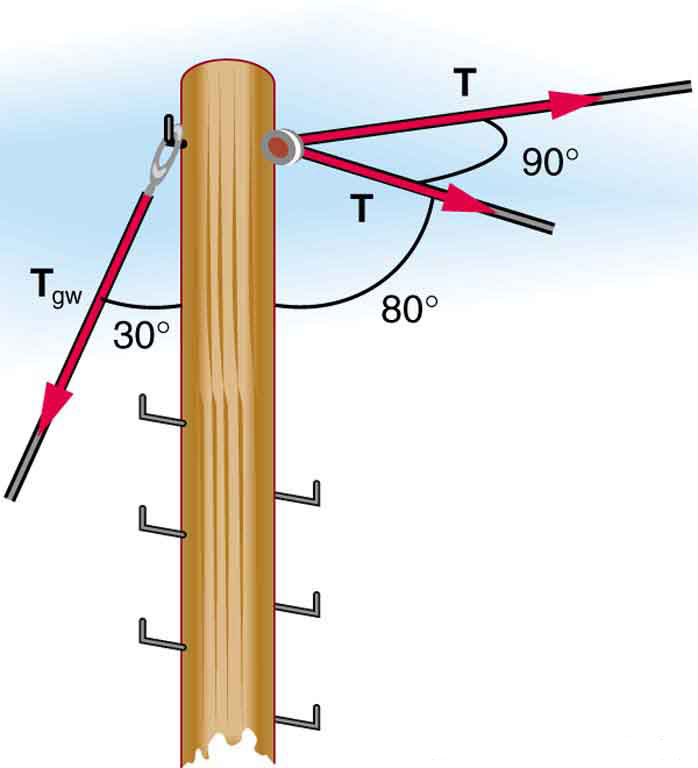
- The pole in Figure 32.9 is at a [latex]\text{90.0º}[/latex] bend in a power line and is therefore subjected to more shear force than poles in straight parts of the line. The tension in each line is [latex]4\text{.}\text{00}×{\text{10}}^{4}\phantom{\rule{0.25em}{0ex}}N[/latex], at the angles shown. The pole is 15.0 m tall, has an 18.0 cm diameter, and can be considered to have half the stiffness of hardwood. (a) Calculate the compression of the pole. (b) Find how much it bends and in what direction. (c) Find the tension in a guy wire used to keep the pole straight if it is attached to the top of the pole at an angle of [latex]\text{30.0º}[/latex] with the vertical. (Clearly, the guy wire must be in the opposite direction of the bend.)
Glossary
- deformation
- change in shape due to the application of force
- Hooke’s law
- proportional relationship between the force [latex]F[/latex] on a material and the deformation [latex]\Delta L[/latex] it causes, tensile strength the breaking stress that will cause permanent deformation or fraction of a material
- stress
- ratio of force to area
- strain
- ratio of change in length to original length
- shear deformation
- deformation perpendicular to the original length of an object
change in shape due to the application of force
proportional relationship between the force [latex]F[/latex] on a material and the deformation [latex]\Delta L[/latex] it causes, tensile strength the breaking stress that will cause permanent deformation or fraction of a material
ratio of force to area
ratio of change in length to original length
deformation perpendicular to the original length of an object

