Linear Momentum and Collisions
55 Elastic Collisions in One Dimension
Learning Objectives
- Describe an elastic collision between two objects in one dimension.
- Define internal kinetic energy and its conservation.
- Derive the condition for conservation of internal kinetic energy.
- Determine final velocities of two objects in an elastic collision given masses and initial velocities.
Collisions occur in many biological and physical systems—from molecules colliding in a gas to cells interacting in a bloodstream. Understanding how momentum and energy are transferred in these events helps us understand many real-world processes. In this section, we begin with the simplest type of collision: a one-dimensional interaction between two objects.
We specifically focus on elastic collisions, which are idealized events in which both momentum and internal kinetic energy are conserved. Internal kinetic energy is the total kinetic energy of all objects within a system. In an elastic collision, this total remains unchanged before and after the event.
Elastic Collision
An elastic collision is one in which both momentum and internal kinetic energy are conserved.
Internal Kinetic Energy
Internal kinetic energy refers to the total kinetic energy of all objects in a system. It does not include potential energy or energy lost to sound, heat, or deformation.
Elastic collisions are common in the microscopic world. For example, electrons colliding with atomic nuclei can be very nearly perfectly elastic. At the macroscopic scale, however, some kinetic energy is usually converted into sound, thermal energy, or deformation. But under carefully controlled conditions, such as when two steel blocks slide on an icy surface or when two carts with spring bumpers collide on a nearly frictionless air track, we can closely approximate elastic behavior.
Figure 55.1 shows a classic one-dimensional elastic collision: two objects interact on a frictionless surface, conserving both momentum and internal kinetic energy.
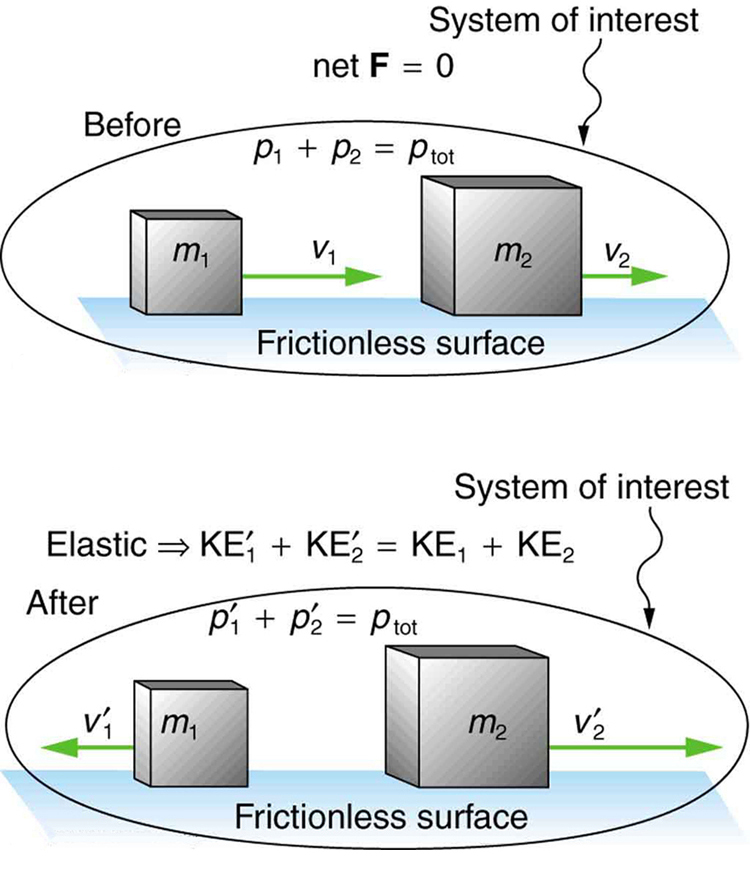
To analyze elastic collisions, we use two conservation laws: conservation of momentum and conservation of internal kinetic energy. The conservation of momentum for two objects in one dimension is written as:
Expanding this using mass and velocity:
Here, [latex]v_1[/latex] and [latex]v_2[/latex] are the initial velocities of objects 1 and 2, and [latex]v'_1[/latex] and [latex]v'_2[/latex] are their final velocities after the collision. Primes (‘) denote quantities after the interaction.
For an elastic collision, we also conserve internal kinetic energy. This gives us the second equation:
Together, these two equations allow us to solve for the unknown final velocities in an elastic collision.
Example 55.1: Calculating Velocities Following an Elastic Collision
Calculate the velocities of two objects following an elastic collision, given that
Strategy and Concept
First, visualize what the initial conditions mean—a small object strikes a larger object that is initially at rest. This situation is slightly simpler than the situation shown in Figure 55.1 where both objects are initially moving. We are asked to find two unknowns (the final velocities [latex]{v\prime }_{1}[/latex] and [latex]{v\prime }_{2}[/latex]). To find two unknowns, we must use two independent equations. Because this collision is elastic, we can use the above two equations. Both can be simplified by the fact that object 2 is initially at rest, and thus [latex]{v}_{2}=0[/latex]. Once we simplify these equations, we combine them algebraically to solve for the unknowns.
Solution
For this problem, note that [latex]{v}_{2}=0[/latex] and use conservation of momentum. Thus,
or
Using conservation of internal kinetic energy and that [latex]{v}_{2}=0[/latex],
Solving the first equation (momentum equation) for [latex]{v\prime }_{2}[/latex], we obtain
Substituting this expression into the second equation (internal kinetic energy equation) eliminates the variable [latex]{v\prime }_{2}[/latex], leaving only [latex]{v\prime }_{1}[/latex] as an unknown (the algebra is left as an exercise for the reader). There are two solutions to any quadratic equation; in this example, they are
and
As noted when quadratic equations were encountered in earlier chapters, both solutions may or may not be meaningful. In this case, the first solution is the same as the initial condition. The first solution thus represents the situation before the collision and is discarded. The second solution [latex]\left({v\prime }_{1}=-3\text{.}\text{00 m/s}\right)[/latex] is negative, meaning that the first object bounces backward. When this negative value of [latex]{v\prime }_{1}[/latex] is used to find the velocity of the second object after the collision, we get
or
Discussion
The result of this example is intuitively reasonable. A small object strikes a larger one at rest and bounces backward. The larger one is knocked forward, but with a low speed. (This is like a compact car bouncing backward off a full-size SUV that is initially at rest.) As a check, try calculating the internal kinetic energy before and after the collision. You will see that the internal kinetic energy is unchanged at 4.00 J. Also check the total momentum before and after the collision; you will find it, too, is unchanged.
The equations for conservation of momentum and internal kinetic energy as written above can be used to describe any one-dimensional elastic collision of two objects. These equations can be extended to more objects if needed.
Making Connections: Take-Home Investigation—Ice Cubes and Elastic Collisions
Find two or more ice cubes of similar size and use a smooth surface such as a glass tabletop or kitchen counter. Set the ice cubes several centimeters apart. Gently flick one ice cube so it slides across the surface and collides with another stationary ice cube. Observe what happens after the collision.
To get the clearest results, try to avoid glancing or spinning collisions. Instead, aim for straight-on impacts with little to no rotation. Watch carefully how the ice cubes move before and after the collision. Does the moving ice cube slow down while the stationary one begins to move? Are the total speeds before and after the collision roughly the same?
Use what you’ve learned about momentum conservation to explain the outcome. Since friction is minimal on the cold, smooth surface, these ice cube collisions may approximate elastic collisions. In such cases, both total momentum and internal kinetic energy are nearly conserved.
PhET Explorations: Collision Lab
Use the PhET Collision Lab simulation to explore how momentum and kinetic energy behave during collisions. This virtual air hockey table lets you customize different aspects of collisions and analyze the outcomes in a frictionless environment.
Suggested Investigations
- Number of Objects: Begin with two discs, then try adding a third. Observe how the system’s total momentum behaves before and after each collision.
- Vary the Masses: Change the mass of one disc. How does this affect the velocities of the discs after collision?
- Initial Conditions: Try different combinations of initial velocities and directions. Investigate both head-on (one-dimensional) and angled (two-dimensional) collisions.
- Check Momentum Conservation: Use the simulation’s built-in data readouts to verify whether total momentum (vector sum) is conserved before and after the collision.
- Check Kinetic Energy Conservation: Compare the total kinetic energy before and after the collision. In which cases is it conserved? When is it not?
- Explore Elasticity: Use the “elasticity slider” to adjust from perfectly elastic to perfectly inelastic collisions. Observe how the conservation of kinetic energy changes with elasticity.
Reflection Questions
- In what scenarios is kinetic energy conserved, and in what scenarios is it not? How does that relate to the elasticity setting?
- Is momentum always conserved, even when kinetic energy is not? Why?
- How might these principles apply in biological or medical contexts, such as understanding how car collisions affect the human body?
This simulation provides an ideal tool to visualize and explore the principles of momentum and energy conservation. Try different setups and interpret the physical meaning behind the graphs and values provided.
Section Summary
- An elastic collision is one in which internal kinetic energy is conserved in addition to momentum.
- When both momentum and kinetic energy are conserved, we can use these principles to calculate the final velocities of the objects involved in a one-dimensional, two-body collision.
- This analysis is especially useful when studying systems with minimal energy loss, such as collisions between low-friction carts, subatomic particles, or ice cubes on a smooth surface.
- Although most macroscopic collisions are not perfectly elastic, they can often be approximated as such in controlled environments, allowing for meaningful application of conservation laws.
Conceptual Questions
- What is an elastic collision?
Problems & Exercises
- Two identical objects (such as billiard balls) have a one-dimensional collision in which one is initially motionless. After the collision, the moving object is stationary and the other moves with the same speed as the other originally had. Show that both momentum and kinetic energy are conserved.
- Professional Application Two manned satellites approach one another at a relative speed of 0.250 m/s, intending to dock. The first has a mass of [latex]4\text{.}\text{00}×{\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}\text{kg}[/latex], and the second a mass of [latex]7\text{.}\text{50}×{\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}\text{kg}[/latex]. If the two satellites collide elastically rather than dock, what is their final relative velocity?
- A 70.0-kg ice hockey goalie, originally at rest, catches a 0.150-kg hockey puck slapped at him at a velocity of 35.0 m/s. Suppose the goalie and the ice puck have an elastic collision and the puck is reflected back in the direction from which it came. What would their final velocities be in this case?
Glossary
- elastic collision
- a collision that also conserves internal kinetic energy
- internal kinetic energy
- the sum of the kinetic energies of the objects in a system
a collision that also conserves internal kinetic energy
the sum of the kinetic energies of the objects in a system
