Density

Saul Beceiro-Novo

Fluid Statics

76 Density

Learning Objectives

Define density.
Calculate the massof a reservoir using its density and volume.
Compare and contrast the densities of various biological and physical substances.

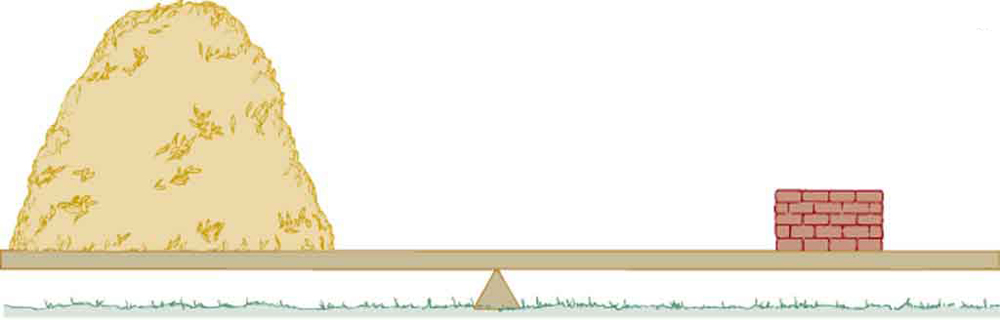
Which weighs more, a ton of feathers or a ton of bricks? This classic riddle draws attention to the difference between mass and density. Although both have the same mass (a ton), feathers take up much more space because their density is much lower than that of bricks. (See Figure 76.1.)

Density is a key physical property used in many scientific and clinical applications—for example, determining if an object floats in water, comparing the composition of tissues, or evaluating whether a substance will disperse or settle in a solution.

Density is defined as the mass per unit volume of a substance:

[latex]\rho = \frac{m}{V}[/latex]

Here, [latex]\rho[/latex] (rho) is the density, [latex]m[/latex] is the mass, and [latex]V[/latex] is the volume. The SI unit of density is [latex]\text{kg/m}^3[/latex], although [latex]\text{g/cm}^3[/latex] or [latex]\text{g/mL}[/latex] are also commonly used in medicine and biology.

Key Concept: Density

Density tells us how much mass is packed into a given volume. Substances with high density (like bone or lead) contain more matter per unit volume than low-density substances (like fat or air).

In the riddle, a ton of feathers takes up much more space than a ton of bricks because feathers have a low density. This volume difference is key in applications like lung imaging, blood analysis, or measuring body composition.

Table 76.1 shows the densities of various solids, liquids, and gases relevant to physics, biology, and environmental science. Note that gases have significantly lower densities than liquids or solids due to the greater spacing between their molecules.

Table 76.1 Densities of Various Substances
Substance	[latex]\rho ({\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}{\text{kg/m}}^{3}\phantom{\rule{0.25em}{0ex}}[/latex] [latex]\text{or}\phantom{\rule{0.25em}{0ex}}\text{g/mL})[/latex]	Substance	[latex]\rho ({\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}{\text{kg/m}}^{3}\phantom{\rule{0.25em}{0ex}}[/latex] [latex]\text{or}\phantom{\rule{0.25em}{0ex}}\text{g/mL})[/latex]	Substance	[latex]\rho ({\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}{\text{kg/m}}^{3}\phantom{\rule{0.25em}{0ex}}[/latex] [latex]\text{or}\phantom{\rule{0.25em}{0ex}}\text{g/mL})[/latex]
Solids		Liquids		Gases
Aluminum	2.7	Water (4ºC)	1.000	Air	[latex]1\text{.}\text{29}×{\text{10}}^{-3}[/latex]
Brass	8.44	Blood	1.05	Carbon dioxide	[latex]1\text{.}\text{98}×{\text{10}}^{-3}[/latex]
Copper (average)	8.8	Sea water	1.025	Carbon monoxide	[latex]1\text{.}\text{25}×{\text{10}}^{-3}[/latex]
Gold	19.32	Mercury	13.6	Hydrogen	[latex]0\text{.}\text{090}×{\text{10}}^{-3}[/latex]
Iron or steel	7.8	Ethyl alcohol	0.79	Helium	[latex]0\text{.}\text{18}×{\text{10}}^{-3}[/latex]
Lead	11.3	Petrol	0.68	Methane	[latex]0\text{.}\text{72}×{\text{10}}^{-3}[/latex]
Polystyrene	0.10	Glycerin	1.26	Nitrogen	[latex]1\text{.}\text{25}×{\text{10}}^{-3}[/latex]
Tungsten	19.30	Olive oil	0.92	Nitrous oxide	[latex]1\text{.}\text{98}×{\text{10}}^{-3}[/latex]
Uranium	18.70			Oxygen	[latex]1\text{.}\text{43}×{\text{10}}^{-3}[/latex]
Concrete	2.30–3.0			Steam [latex]\left(\text{100º C}\right)[/latex]	[latex]0\text{.}\text{60}×{\text{10}}^{-3}[/latex]
Cork	0.24
Glass, common (average)	2.6
Granite	2.7
Earth’s crust	3.3
Wood	0.3–0.9
Ice (0°C)	0.917
Bone	1.7–2.0

A pile of feathers measuring a ton and a ton of bricks are placed on either side of a plank that is balanced on a small support. — Figure 76.1 A ton of feathers and a ton of bricks have the same mass, but the feathers make a much bigger pile because they have a much lower density.

Example 76.1: Calculating the Mass of a Reservoir

Problem: A reservoir has a surface area of [latex]50.0 \, \text{km}^2[/latex] and an average depth of [latex]40.0 \, \text{m}[/latex]. What is the total mass of water in the reservoir? (See Figure 76.2 for a view of a large reservoir—the Three Gorges Dam site on the Yangtze River in central China.)

Strategy

We use the formula for density:

[latex]\rho = \frac{m}{V} \Rightarrow m = \rho V[/latex]

The volume [latex]V[/latex] of the reservoir is calculated from its surface area [latex]A[/latex] and depth [latex]h[/latex]:

[latex]V = A \cdot h = (50.0 \times 10^6 \, \text{m}^2)(40.0 \, \text{m}) = 2.00 \times 10^9 \, \text{m}^3[/latex]

Using [latex]\rho = 1.00 \times 10^3 \, \text{kg/m}^3[/latex] for water, we find:

[latex]m = (1.00 \times 10^3 \, \text{kg/m}^3)(2.00 \times 10^9 \, \text{m}^3) = 2.00 \times 10^{12} \, \text{kg}[/latex]

Discussion

The reservoir contains over 2 trillion kilograms of water. This mass plays a critical role in hydroelectric energy production, flood control, and ecological balance.

Photograph of the Three Gorges Dam in central China. — Figure 76.2 The Three Gorges Dam in China is one of the largest hydroelectric power generators in the world. The immense mass of water behind it demonstrates the importance of density in engineering and environmental planning. (credit: Le Grand Portage)

Take-Home Experiment: Sugar vs. Salt

Take equal volumes of sugar and salt. Which one is heavier? The difference in weight comes from their different densities and crystalline structures. Try measuring mass and volume to calculate density yourself!

Section Summary

Density is a measure of how much mass is contained in a given volume:
[latex]\rho = \frac{m}{V}[/latex]
The SI unit for density is [latex]\text{kg/m}^3[/latex], though [latex]\text{g/cm}^3[/latex] or [latex]\text{g/mL}[/latex] are often used in medical contexts.
Knowing the density of a substance helps predict whether it will float or sink, estimate composition, or calculate mass from volume in real-world problems.

Conceptual Questions

Approximately how does the density of air vary with altitude?
Give an example in which density is used to identify the substance composing an object. Would information in addition to average density be needed to identify the substances in an object composed of more than one material?
Figure 76.3 shows a glass of ice water filled to the brim. Will the water overflow when the ice melts? Explain your answer.

Figure 76.3

Problems & Exercises

Gold is sold by the troy ounce (31.103 g). What is the volume of 1 troy ounce of pure gold?
Mercury is commonly supplied in flasks containing 34.5 kg (about 76 lb). What is the volume in liters of this much mercury?
(a) What is the mass of a deep breath of air having a volume of 2.00 L? (b) Discuss the effect taking such a breath has on your body’s volume and density.
A straightforward method of finding the density of an object is to measure its mass and then measure its volume by submerging it in a graduated cylinder. What is the density of a 240-g rock that displaces [latex]\text{89}\text{.}0\phantom{\rule{0.25em}{0ex}}{\text{cm}}^{3}[/latex] of water? (Note that the accuracy and practical applications of this technique are more limited than a variety of others that are based on Archimedes’ principle.)
Suppose you have a coffee mug with a circular cross section and vertical sides (uniform radius). What is its inside radius if it holds 375 g of coffee when filled to a depth of 7.50 cm? Assume coffee has the same density as water.
(a) A rectangular gasoline tank can hold 50.0 kg of gasoline when full. What is the depth of the tank if it is 0.500-m wide by 0.900-m long? (b) Discuss whether this gas tank has a reasonable volume for a passenger car.
A trash compactor can reduce the volume of its contents to 0.350 their original value. Neglecting the mass of air expelled, by what factor is the density of the rubbish increased?
A 2.50-kg steel gasoline can holds 20.0 L of gasoline when full. What is the average density of the full gas can, taking into account the volume occupied by steel as well as by gasoline?
What is the density of 18.0-karat gold that is a mixture of 18 parts gold, 5 parts silver, and 1 part copper? (These values are parts by mass, not volume.) Assume that this is a simple mixture having an average density equal to the weighted densities of its constituents.
There is relatively little empty space between atoms in solids and liquids, so that the average density of an atom is about the same as matter on a macroscopic scale—approximately [latex]{\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}{\text{kg/m}}^{3}[/latex]. The nucleus of an atom has a radius about [latex]{\text{10}}^{-5}[/latex] that of the atom and contains nearly all the mass of the entire atom. (a) What is the approximate density of a nucleus? (b) One remnant of a supernova, called a neutron star, can have the density of a nucleus. What would be the radius of a neutron star with a mass 10 times that of our Sun (the radius of the Sun is [latex]7×{\text{10}}^{8}\phantom{\rule{0.25em}{0ex}}\text{m}[/latex])?