Oscillatory Motion and Waves and Physics of Hearing.
122 Damped Harmonic Motion
Learning Objectives
- Compare and discuss underdamped and overdamped oscillating systems.
- Explain the behavior of a critically damped system.

A plucked guitar string vibrates briefly before coming to rest. Likewise, a child on a swing will eventually stop unless pushed repeatedly. These are examples of damping, which is the gradual loss of energy in an oscillating system. While we often strive to reduce damping in ideal physics models, in real-world systems damping is nearly always present. In some applications, such as car suspension systems, damping is not just present—it is essential.
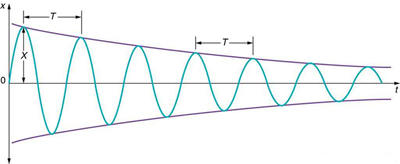
When damping is small, the system still oscillates with nearly the same period and frequency as an ideal simple harmonic oscillator, but the amplitude gradually decreases, as shown in Figure 122.2. This decrease occurs because energy is continually lost—often as thermal energy—due to a non-conservative damping force. The energy loss is described by:
Here, [latex]W_{\text{nc}}[/latex] is the work done by non-conservative forces. In a damped system, [latex]W_{\text{nc}}[/latex] is negative, indicating that energy is being removed from the system.
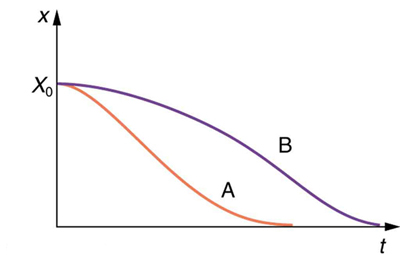
As damping increases, the oscillations slow down and the period lengthens because the damping force opposes motion. With very strong damping, the system no longer oscillates—it slowly returns to equilibrium without crossing it. Figure 122.3 compares different damping conditions:
- Curve A shows a critically damped system, where the system returns to equilibrium as quickly as possible without oscillating.
- Curve B represents an overdamped system, which also does not oscillate but returns to equilibrium more slowly.
- Underdamped systems (not shown here) return to equilibrium with decreasing oscillations and overshoot the rest position one or more times.
Critical damping is often desirable in systems that must return quickly to equilibrium without oscillations. For instance, bathroom scales with needle gauges are designed to be critically damped so that the needle settles promptly at your weight without bouncing around.
In engineering and biology, damping forces vary depending on the system. Some are nearly independent of velocity (as in dry friction), while others are directly proportional to velocity. In biological tissues and fluid systems, damping often arises from internal viscosity and plays a role in processes ranging from heartbeat rhythms to the design of medical imaging devices.
Example 122.1: Damping an Oscillatory Motion: Friction on an Object Connected to a Spring
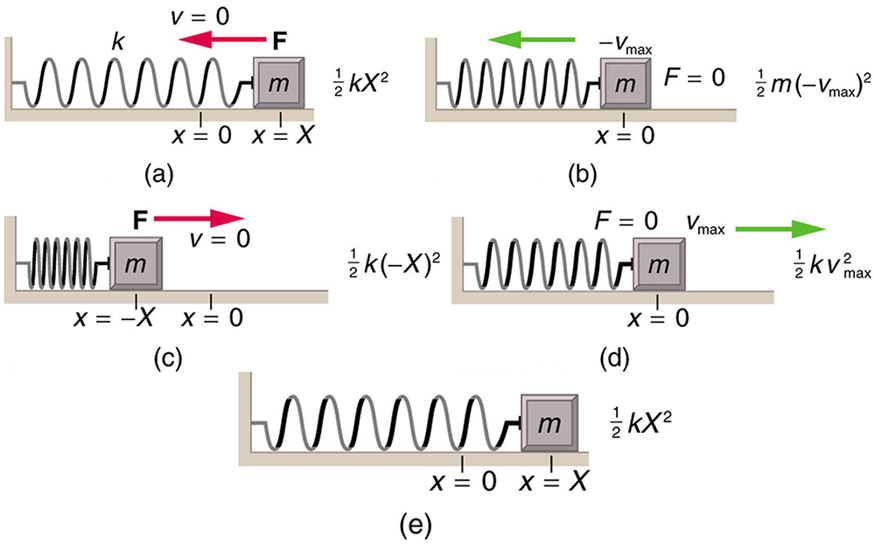
Damping oscillatory motion is important in many systems, and the ability to control the damping is even more so. This is generally attained using non-conservative forces such as the friction between surfaces, and viscosity for objects moving through fluids. The following example considers friction. Suppose a 0.200-kg object is connected to a spring as shown in Figure 122.4, but there is simple friction between the object and the surface, and the coefficient of friction [latex]{\mu }_{k}[/latex] is equal to 0.0800. (a) What is the frictional force between the surfaces? (b) What total distance does the object travel if it is released 0.100 m from equilibrium, starting at [latex]v=0[/latex]? The force constant of the spring is [latex]k=\text{50}\text{.}0 N/m\text{}[/latex].
Strategy
This problem requires you to integrate your knowledge of various concepts regarding waves, oscillations, and damping. To solve an integrated concept problem, you must first identify the physical principles involved. Part (a) is about the frictional force. This is a topic involving the application of Newton’s Laws. Part (b) requires an understanding of work and conservation of energy, as well as some understanding of horizontal oscillatory systems.
Now that we have identified the principles we must apply in order to solve the problems, we need to identify the knowns and unknowns for each part of the question, as well as the quantity that is constant in Part (a) and Part (b) of the question.
Solution a
- Choose the proper equation: Friction is [latex]f={\mu }_{k}\text{mg}[/latex].
- Identify the known values.
- Enter the known values into the equation:
[latex]f=\text{(0.0800)}(0\text{.200 kg)}(9\text{.80 m}/{\text{s}}^{\text{2}}\text{)}.[/latex]
- Calculate and convert units:
[latex]f=\text{0.157 N}.[/latex]
Discussion a
The force here is small because the system and the coefficients are small.
Solution b
Identify the known:
- The system involves elastic potential energy as the spring compresses and expands, friction that is related to the work done, and the kinetic energy as the body speeds up and slows down.
- Energy is not conserved as the mass oscillates because friction is a non-conservative force.
- The motion is horizontal, so gravitational potential energy does not need to be considered.
- Because the motion starts from rest, the energy in the system is initially [latex]{\text{PE}}_{\mathrm{el,i}}=\left(1/2\right){\text{kX}}^{2}[/latex]. This energy is removed by work done by friction [latex]{W}_{\text{nc}}=–\text{fd}[/latex], where
[latex]d[/latex]
is the total distance traveled and [latex]f={\mu }_{\text{k}}\text{mg}[/latex] is the force of friction. When the system stops moving, the friction force will balance the force exerted by the spring, so [latex]{\text{PE}}_{\text{e1,f}}=\left(1/2\right){\text{kx}}^{2}[/latex] where [latex]x[/latex] is the final position and is given by[latex]\begin{array}{lll}{F}_{\text{el}}& =& f\\ \text{kx}& =& {\mu }_{\text{k}}\text{mg}\\ x& =& \frac{{\mu }_{\text{k}}\text{mg}}{k}\end{array}.[/latex]
- By equating the work done to the energy removed, solve for the distance
[latex]d[/latex]
. - The work done by the non-conservative forces equals the initial, stored elastic potential energy. Identify the correct equation to use:
[latex]{\text{W}}_{\text{nc}}=\Delta \left(\text{KE}+\text{PE}\right)={\text{PE}}_{\text{el,f}}-{\text{PE}}_{\text{el,i}}=\frac{1}{2}k\left({\left(\frac{{\mu }_{k}\mathit{\text{mg}}}{k}\right)}^{2}-{X}^{2}\right).[/latex]
- Recall that [latex]{W}_{\text{nc}}=–\text{fd}[/latex].
- Enter the friction as [latex]f={\mu }_{\text{k}}\text{mg}[/latex] into [latex]{W}_{\text{nc}}=–\text{fd}[/latex], thus
[latex]{W}_{\text{nc}}={–\mu }_{\text{k}}\text{mgd}.[/latex]
- Combine these two equations to find
[latex]\frac{1}{2}k\left({\left(\frac{{\mu }_{k}\text{mg}}{k}\right)}^{2}-{X}^{2}\right)=-{\mu }_{\text{k}}\text{mgd}.[/latex]
- Solve the equation for
[latex]d[/latex]
:[latex]d=\frac{\text{k}}{{\text{2}\mu }_{\text{k}}\text{mg}}\left({X}^{2}–{\left(\frac{{\mu }_{\text{k}}\text{mg}}{k}\right)}^{2}\right).[/latex] - Enter the known values into the resulting equation:
[latex]d=\frac{\text{50}\text{.}0 N/m\text{}}{2\left(0\text{.}\text{0800}\right)\left(0\text{.}\text{200}\phantom{\rule{0.25em}{0ex}}\text{kg}\right)\left(9\text{.}\text{80}\phantom{\rule{0.25em}{0ex}}{\text{m/s}}^{2}\right)}\left({\left(0\text{.}\text{100}\phantom{\rule{0.25em}{0ex}}\text{m}\right)}^{2}-{\left(\frac{\left(0\text{.}\text{0800}\right)\left(0\text{.}\text{200}\phantom{\rule{0.25em}{0ex}}\text{kg}\right)\left(9\text{.}\text{80}\phantom{\rule{0.25em}{0ex}}{\text{m/s}}^{2}\right)}{\text{50}\text{.}0\phantom{\rule{0.25em}{0ex}}\text{N/m}}\right)}^{2}\right).[/latex]
- Calculate
[latex]d[/latex]
and convert units:[latex]d=1\text{.}\text{59}\phantom{\rule{0.25em}{0ex}}\text{m}.[/latex]
Discussion b
This is the total distance traveled back and forth across [latex]x=0[/latex], which is the undamped equilibrium position. The number of oscillations about the equilibrium position will be more than [latex]d/X=\left(1\text{.}\text{59}\phantom{\rule{0.25em}{0ex}}\text{m}\right)/\left(0\text{.}\text{100}\phantom{\rule{0.25em}{0ex}}\text{m}\right)=\text{15}\text{.}9[/latex] because the amplitude of the oscillations is decreasing with time. At the end of the motion, this system will not return to [latex]x=0[/latex] for this type of damping force, because static friction will exceed the restoring force. This system is underdamped. In contrast, an overdamped system with a simple constant damping force would not cross the equilibrium position [latex]x=0[/latex] a single time. For example, if this system had a damping force 20 times greater, it would only move 0.0484 m toward the equilibrium position from its original 0.100-m position.
This worked example illustrates how to apply problem-solving strategies to situations that integrate the different concepts you have learned. The first step is to identify the physical principles involved in the problem. The second step is to solve for the unknowns using familiar problem-solving strategies. These are found throughout the text, and many worked examples show how to use them for single topics. In this integrated concepts example, you can see how to apply them across several topics. You will find these techniques useful in applications of physics outside a physics course, such as in your profession, in other science disciplines, and in everyday life.
Check Your Understanding
Question: Why are completely undamped harmonic oscillators so rare?
Answer: In real-world systems, friction is almost always present. Friction and other resistive forces cause energy to dissipate, resulting in ]damping. This energy loss prevents sustained undamped motion, making completely undamped harmonic oscillators practically impossible outside of idealized models.
Question: Describe the difference between overdamping, underdamping, and critical damping.
Answer: In an overdamped system, the return to equilibrium is slow and does not involve oscillations. An underdamped system returns more quickly to equilibrium but oscillates through the equilibrium position with decreasing amplitude. A critically damped system returns to equilibrium in the shortest time possible without oscillating.
Section Summary
- Damped harmonic oscillators experience energy dissipation due to non-conservative forces like friction and air resistance.
- Critical damping allows the system to return to equilibrium rapidly without oscillation or overshooting.
- An underdamped system oscillates through the equilibrium position with diminishing amplitude.
- An overdamped system returns to equilibrium more slowly than a critically damped system and does not oscillate.
Conceptual Questions
- Give an example of a damped harmonic oscillator. (They are more common than undamped or simple harmonic oscillators.)
- How would a car bounce after a bump under each of these conditions?
- overdamping
- underdamping
- critical damping
- Most harmonic oscillators are damped and, if undriven, eventually come to a stop. How is this observation related to the second law of thermodynamics?
Problems & Exercises
- The amplitude of a lightly damped oscillator decreases by [latex]3\text{.}0%\text{}[/latex] during each cycle. What percentage of the mechanical energy of the oscillator is lost in each cycle?
Glossary
- critical damping
- the condition in which the damping of an oscillator causes it to return as quickly as possible to its equilibrium position without oscillating back and forth about this position
- over damping
- the condition in which damping of an oscillator causes it to return to equilibrium without oscillating; oscillator moves more slowly toward equilibrium than in the critically damped system
- under damping
- the condition in which damping of an oscillator causes it to return to equilibrium with the amplitude gradually decreasing to zero; system returns to equilibrium faster but overshoots and crosses the equilibrium position one or more times.
-
- damping
- the gradual loss of amplitude in an oscillating system due to energy being dissipated, typically as heat, sound, or other forms of energy. Damping reduces the system’s motion over time and can be caused by friction, air resistance, or internal material resistance.
the condition in which damping of an oscillator causes it to return to equilibrium with the amplitude gradually decreasing to zero; system returns to equilibrium faster but overshoots and crosses the equilibrium position one or more times
the condition in which the damping of an oscillator causes it to return as quickly as possible to its equilibrium position without oscillating back and forth about this position
time it takes to complete one oscillation
number of events per unit of time
the energy within an object due to the random motion of its atoms and molecules that accounts for the object's temperature
The gradual loss of amplitude in an oscillating system due to energy being dissipated, typically as heat, sound, or other forms of energy. Damping reduces the system’s motion over time and can be caused by friction, air resistance, or internal material resistance.
the condition in which damping of an oscillator causes it to return to equilibrium without oscillating; oscillator moves more slowly toward equilibrium than in the critically damped system
a force whose work depends on the path followed between the given initial and final configurations
Learning Objectives
- Compare and discuss underdamped and overdamped oscillating systems.
- Explain the behavior of a critically damped system.

A plucked guitar string vibrates briefly before coming to rest. Likewise, a child on a swing will eventually stop unless pushed repeatedly. These are examples of damping, which is the gradual loss of energy in an oscillating system. While we often strive to reduce damping in ideal physics models, in real-world systems damping is nearly always present. In some applications, such as car suspension systems, damping is not just present—it is essential.
When damping is small, the system still oscillates with nearly the same period and frequency as an ideal simple harmonic oscillator, but the amplitude gradually decreases, as shown in Figure 122.2. This decrease occurs because energy is continually lost—often as thermal energy—due to a non-conservative damping force. The energy loss is described by:
Here, [latex]W_{\text{nc}}[/latex] is the work done by non-conservative forces. In a damped system, [latex]W_{\text{nc}}[/latex] is negative, indicating that energy is being removed from the system.

As damping increases, the oscillations slow down and the period lengthens because the damping force opposes motion. With very strong damping, the system no longer oscillates—it slowly returns to equilibrium without crossing it. Figure 122.3 compares different damping conditions:
- Curve A shows a critically damped system, where the system returns to equilibrium as quickly as possible without oscillating.
- Curve B represents an overdamped system, which also does not oscillate but returns to equilibrium more slowly.
- Underdamped systems (not shown here) return to equilibrium with decreasing oscillations and overshoot the rest position one or more times.

Critical damping is often desirable in systems that must return quickly to equilibrium without oscillations. For instance, bathroom scales with needle gauges are designed to be critically damped so that the needle settles promptly at your weight without bouncing around.
In engineering and biology, damping forces vary depending on the system. Some are nearly independent of velocity (as in dry friction), while others are directly proportional to velocity. In biological tissues and fluid systems, damping often arises from internal viscosity and plays a role in processes ranging from heartbeat rhythms to the design of medical imaging devices.
Example 122.1: Damping an Oscillatory Motion: Friction on an Object Connected to a Spring
Damping oscillatory motion is important in many systems, and the ability to control the damping is even more so. This is generally attained using non-conservative forces such as the friction between surfaces, and viscosity for objects moving through fluids. The following example considers friction. Suppose a 0.200-kg object is connected to a spring as shown in Figure 122.4, but there is simple friction between the object and the surface, and the coefficient of friction [latex]{\mu }_{k}[/latex] is equal to 0.0800. (a) What is the frictional force between the surfaces? (b) What total distance does the object travel if it is released 0.100 m from equilibrium, starting at [latex]v=0[/latex]? The force constant of the spring is [latex]k=\text{50}\text{.}0 N/m\text{}[/latex].

Strategy
This problem requires you to integrate your knowledge of various concepts regarding waves, oscillations, and damping. To solve an integrated concept problem, you must first identify the physical principles involved. Part (a) is about the frictional force. This is a topic involving the application of Newton’s Laws. Part (b) requires an understanding of work and conservation of energy, as well as some understanding of horizontal oscillatory systems.
Now that we have identified the principles we must apply in order to solve the problems, we need to identify the knowns and unknowns for each part of the question, as well as the quantity that is constant in Part (a) and Part (b) of the question.
Solution a
- Choose the proper equation: Friction is [latex]f={\mu }_{k}\text{mg}[/latex].
- Identify the known values.
- Enter the known values into the equation:
[latex]f=\text{(0.0800)}(0\text{.200 kg)}(9\text{.80 m}/{\text{s}}^{\text{2}}\text{)}.[/latex]
- Calculate and convert units:
[latex]f=\text{0.157 N}.[/latex]
Discussion a
The force here is small because the system and the coefficients are small.
Solution b
Identify the known:
- The system involves elastic potential energy as the spring compresses and expands, friction that is related to the work done, and the kinetic energy as the body speeds up and slows down.
- Energy is not conserved as the mass oscillates because friction is a non-conservative force.
- The motion is horizontal, so gravitational potential energy does not need to be considered.
- Because the motion starts from rest, the energy in the system is initially [latex]{\text{PE}}_{\mathrm{el,i}}=\left(1/2\right){\text{kX}}^{2}[/latex]. This energy is removed by work done by friction [latex]{W}_{\text{nc}}=–\text{fd}[/latex], where
[latex]d[/latex]
is the total distance traveled and [latex]f={\mu }_{\text{k}}\text{mg}[/latex] is the force of friction. When the system stops moving, the friction force will balance the force exerted by the spring, so [latex]{\text{PE}}_{\text{e1,f}}=\left(1/2\right){\text{kx}}^{2}[/latex] where [latex]x[/latex] is the final position and is given by[latex]\begin{array}{lll}{F}_{\text{el}}& =& f\\ \text{kx}& =& {\mu }_{\text{k}}\text{mg}\\ x& =& \frac{{\mu }_{\text{k}}\text{mg}}{k}\end{array}.[/latex]
- By equating the work done to the energy removed, solve for the distance
[latex]d[/latex]
. - The work done by the non-conservative forces equals the initial, stored elastic potential energy. Identify the correct equation to use:
[latex]{\text{W}}_{\text{nc}}=\Delta \left(\text{KE}+\text{PE}\right)={\text{PE}}_{\text{el,f}}-{\text{PE}}_{\text{el,i}}=\frac{1}{2}k\left({\left(\frac{{\mu }_{k}\mathit{\text{mg}}}{k}\right)}^{2}-{X}^{2}\right).[/latex]
- Recall that [latex]{W}_{\text{nc}}=–\text{fd}[/latex].
- Enter the friction as [latex]f={\mu }_{\text{k}}\text{mg}[/latex] into [latex]{W}_{\text{nc}}=–\text{fd}[/latex], thus
[latex]{W}_{\text{nc}}={–\mu }_{\text{k}}\text{mgd}.[/latex]
- Combine these two equations to find
[latex]\frac{1}{2}k\left({\left(\frac{{\mu }_{k}\text{mg}}{k}\right)}^{2}-{X}^{2}\right)=-{\mu }_{\text{k}}\text{mgd}.[/latex]
- Solve the equation for
[latex]d[/latex]
:[latex]d=\frac{\text{k}}{{\text{2}\mu }_{\text{k}}\text{mg}}\left({X}^{2}–{\left(\frac{{\mu }_{\text{k}}\text{mg}}{k}\right)}^{2}\right).[/latex] - Enter the known values into the resulting equation:
[latex]d=\frac{\text{50}\text{.}0 N/m\text{}}{2\left(0\text{.}\text{0800}\right)\left(0\text{.}\text{200}\phantom{\rule{0.25em}{0ex}}\text{kg}\right)\left(9\text{.}\text{80}\phantom{\rule{0.25em}{0ex}}{\text{m/s}}^{2}\right)}\left({\left(0\text{.}\text{100}\phantom{\rule{0.25em}{0ex}}\text{m}\right)}^{2}-{\left(\frac{\left(0\text{.}\text{0800}\right)\left(0\text{.}\text{200}\phantom{\rule{0.25em}{0ex}}\text{kg}\right)\left(9\text{.}\text{80}\phantom{\rule{0.25em}{0ex}}{\text{m/s}}^{2}\right)}{\text{50}\text{.}0\phantom{\rule{0.25em}{0ex}}\text{N/m}}\right)}^{2}\right).[/latex]
- Calculate
[latex]d[/latex]
and convert units:[latex]d=1\text{.}\text{59}\phantom{\rule{0.25em}{0ex}}\text{m}.[/latex]
Discussion b
This is the total distance traveled back and forth across [latex]x=0[/latex], which is the undamped equilibrium position. The number of oscillations about the equilibrium position will be more than [latex]d/X=\left(1\text{.}\text{59}\phantom{\rule{0.25em}{0ex}}\text{m}\right)/\left(0\text{.}\text{100}\phantom{\rule{0.25em}{0ex}}\text{m}\right)=\text{15}\text{.}9[/latex] because the amplitude of the oscillations is decreasing with time. At the end of the motion, this system will not return to [latex]x=0[/latex] for this type of damping force, because static friction will exceed the restoring force. This system is underdamped. In contrast, an overdamped system with a simple constant damping force would not cross the equilibrium position [latex]x=0[/latex] a single time. For example, if this system had a damping force 20 times greater, it would only move 0.0484 m toward the equilibrium position from its original 0.100-m position.
This worked example illustrates how to apply problem-solving strategies to situations that integrate the different concepts you have learned. The first step is to identify the physical principles involved in the problem. The second step is to solve for the unknowns using familiar problem-solving strategies. These are found throughout the text, and many worked examples show how to use them for single topics. In this integrated concepts example, you can see how to apply them across several topics. You will find these techniques useful in applications of physics outside a physics course, such as in your profession, in other science disciplines, and in everyday life.
Check Your Understanding
Question: Why are completely undamped harmonic oscillators so rare?
Answer: In real-world systems, friction is almost always present. Friction and other resistive forces cause energy to dissipate, resulting in ]damping. This energy loss prevents sustained undamped motion, making completely undamped harmonic oscillators practically impossible outside of idealized models.
Question: Describe the difference between overdamping, underdamping, and critical damping.
Answer: In an overdamped system, the return to equilibrium is slow and does not involve oscillations. An underdamped system returns more quickly to equilibrium but oscillates through the equilibrium position with decreasing amplitude. A critically damped system returns to equilibrium in the shortest time possible without oscillating.
Section Summary
- Damped harmonic oscillators experience energy dissipation due to non-conservative forces like friction and air resistance.
- Critical damping allows the system to return to equilibrium rapidly without oscillation or overshooting.
- An underdamped system oscillates through the equilibrium position with diminishing amplitude.
- An overdamped system returns to equilibrium more slowly than a critically damped system and does not oscillate.
Conceptual Questions
- Give an example of a damped harmonic oscillator. (They are more common than undamped or simple harmonic oscillators.)
- How would a car bounce after a bump under each of these conditions?
- overdamping
- underdamping
- critical damping
- Most harmonic oscillators are damped and, if undriven, eventually come to a stop. How is this observation related to the second law of thermodynamics?
Problems & Exercises
- The amplitude of a lightly damped oscillator decreases by [latex]3\text{.}0%\text{}[/latex] during each cycle. What percentage of the mechanical energy of the oscillator is lost in each cycle?
Glossary
- critical damping
- the condition in which the damping of an oscillator causes it to return as quickly as possible to its equilibrium position without oscillating back and forth about this position
- over damping
- the condition in which damping of an oscillator causes it to return to equilibrium without oscillating; oscillator moves more slowly toward equilibrium than in the critically damped system
- under damping
- the condition in which damping of an oscillator causes it to return to equilibrium with the amplitude gradually decreasing to zero; system returns to equilibrium faster but overshoots and crosses the equilibrium position one or more times.
-
- damping
- the gradual loss of amplitude in an oscillating system due to energy being dissipated, typically as heat, sound, or other forms of energy. Damping reduces the system’s motion over time and can be caused by friction, air resistance, or internal material resistance.

