"

Linear Momentum and Collisions

54 Conservation of Momentum

Learning Objectives

  • Describe the principle of conservation of momentum.
  • Derive the expression for conservation of momentum.
  • Apply momentum conservation to everyday and biological examples.
  • Explain how conservation of momentum applies at the atomic and subatomic levels.

In previous chapters, we examined how impulse changes the momentum of an object due to an external force. But what if there are no net external forces acting on a system? In such cases, the conservation of momentum principle applies: the total momentum of the system remains unchanged.

Momentum is conserved in any isolated system, meaning a system where no net external force acts. This principle is fundamental across physics, biology, and engineering, and helps explain a wide range of physical phenomena—from collisions between vehicles to the motion of molecules in cells.

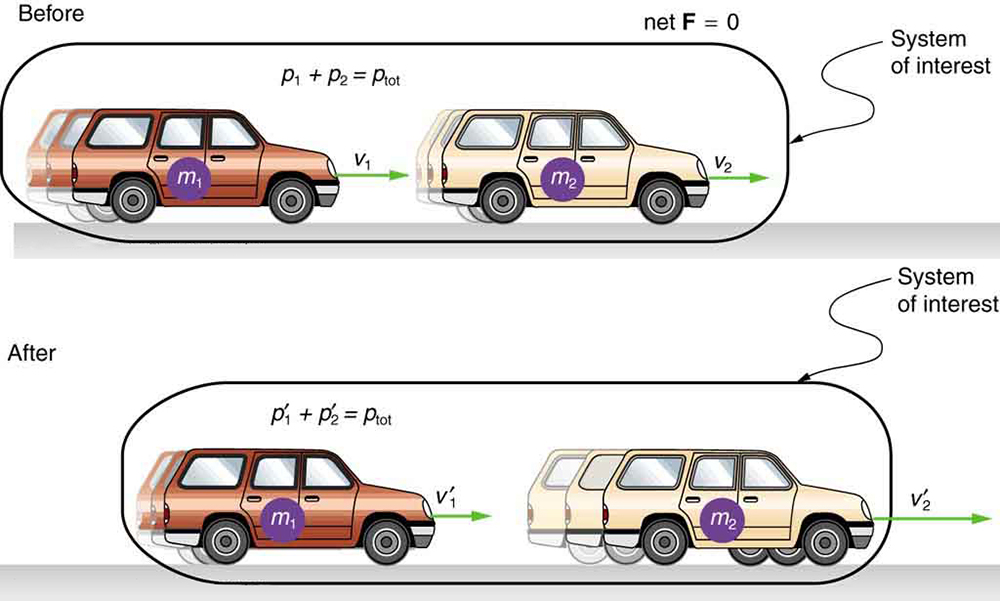
To illustrate this concept, consider two cars colliding on a frictionless road (Figure 54.1). Car 1, with mass [latex]m_1[/latex] and velocity [latex]v_1[/latex], bumps into Car 2, with mass [latex]m_2[/latex] and velocity [latex]v_2[/latex]. After the collision, their velocities change, but if no net external forces act, their total momentum is conserved.

[latex]\Delta p_1 = F_1 \Delta t[/latex]
[latex]\Delta p_2 = F_2 \Delta t[/latex]

According to Newton’s third law, [latex]F_2 = -F_1[/latex], so:

[latex]\Delta p_1 + \Delta p_2 = 0[/latex]

Thus, the total momentum before the collision is equal to the total momentum after the collision:

[latex]p_1 + p_2 = \text{constant}[/latex]
[latex]p_1 + p_2 = p_1' + p_2'[/latex]

This applies not only to two-object systems but to any isolated system with multiple interacting components. More generally, the conservation of momentum is expressed as:

[latex]\mathbf{p}_{\text{tot}} = \text{constant}[/latex]
[latex]\mathbf{p}_{\text{tot}} = \mathbf{p}'_{\text{tot}} \quad (\text{isolated system})[/latex]

An isolated system is defined as one with no net external force:

[latex]\mathbf{F}_{\text{net}} = 0[/latex]

This principle can also be derived from Newton’s second law, expressed in terms of momentum:

[latex]\mathbf{F}_{\text{net}} = \frac{\Delta \mathbf{p}_{\text{tot}}}{\Delta t}[/latex]

If [latex]\mathbf{F}_{\text{net}} = 0[/latex], then [latex]\Delta \mathbf{p}_{\text{tot}} = 0[/latex], which means momentum remains constant.

A brown car with velocity V 1 and mass m 1 moves toward the right behind a tan car of velocity V 2 and mass m 2. The system of interest has a total momentum equal to the sum of individual momentums p 1 and p 2. The net force between them is zero before they collide with one another. The brown car after colliding with the tan car has velocity V 1prime and momentum p 1 prime and the light brown car moves with velocity V 2 prime and momentum p 2 prime. Both move in the same direction as before collision. This system of interest has a total momentum equal to the sum p 1 prime and p 2 prime.
Figure 54.1: A car of mass [latex]{m}_{1}[/latex] moving with a velocity of [latex]{v}_{1}[/latex] bumps into another car of mass [latex]{m}_{2}[/latex] and velocity [latex]{v}_{2}[/latex] that it is following. As a result, the first car slows down to a velocity of [latex]{\mathrm{v\prime }}_{1}[/latex] and the second speeds up to a velocity of [latex]{\mathrm{v\prime }}_{2}[/latex]. The momentum of each car is changed, but the total momentum [latex]{p}_{\text{tot}}[/latex] of the two cars is the same before and after the collision (if you assume friction is negligible).

Momentum in Different Directions

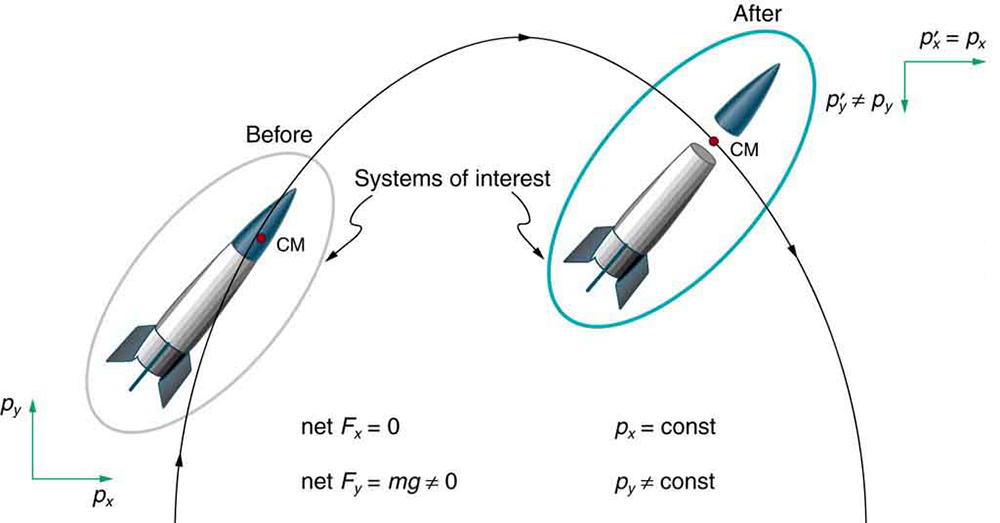
Momentum is a vector quantity, meaning it can be conserved independently in each spatial direction. For instance, in projectile motion, momentum in the horizontal direction is conserved (assuming air resistance is negligible), while in the vertical direction, gravity exerts a net force. However, when analyzing the projectile and Earth as a system, total momentum is conserved in all directions (Figure 54.2).

A space probe is projected upward. It takes a parabolic path. No horizontal net force acts on. The horizontal component of momentum remains conserved. The vertical net force is not zero and the vertical component of momentum is not a constant. When the space probe separates, the horizontal net force remains zero as the force causing separation is internal to the system. The vertical net force is not zero and the vertical component of momentum is also not a constant after separation. The centre of mass however continues in the same parabolic path.
Figure 54.2: The horizontal component of a projectile’s momentum is conserved if air resistance is negligible, even in this case where a space probe separates. The forces causing the separation are internal to the system, so that the net external horizontal force [latex]{F}_{x–\text{net}}[/latex] is still zero. The vertical component of the momentum is not conserved, because the net vertical force [latex]{F}_{y–\text{net}}[/latex] is not zero. In the vertical direction, the space probe-Earth system needs to be considered and we find that the total momentum is conserved. The center of mass of the space probe takes the same path it would if the separation did not occur.

Making Connections: Drop of a Tennis Ball and a Basketball

Try this simple experiment to visualize momentum transfer. Hold a tennis ball and a basketball side by side so they are in contact. Drop them simultaneously. You’ll notice that both balls rebound slightly after hitting the ground. Now repeat the experiment, but this time stack the tennis ball on top of the basketball and drop them together. The basketball hits the ground first, compresses, and rebounds. As it rebounds, it transfers momentum upward into the tennis ball. The tennis ball may shoot upward dramatically, sometimes several times higher than the original drop height. This effect is a result of the conservation of momentum and energy transfer through collision.

Try reversing the positions, holding the basketball above the tennis ball. You’ll likely see the tennis ball remain almost stationary while the basketball rebounds weakly. This demonstrates how the mass and timing of momentum transfer influence the system’s final state.

Making Connections: Two Tennis Balls in a Ballistic Trajectory
Tie two tennis balls together with a short string, about 30 cm in length. Hold one ball and let the other hang freely, then throw the pair in a gentle arc through the air. You’ll notice that the center of mass of the system follows a smooth parabolic trajectory, even though the two balls may swing and rotate.Now mark the midpoint of the string with a bright sticker and repeat the throw. You’ll observe that the sticker follows a clean arc while the balls may oscillate around it. This center point represents the system’s center of mass, which moves according to the conservation of momentum and external forces (mainly gravity). This experiment illustrates how internal motion (oscillations between the balls) doesn’t affect the external path of the system as a whole.

Momentum in Biological Systems: Jellyfish, Squids, and You

Many aquatic animals rely on the conservation of momentum for movement. Jellyfish, for example, draw water into their umbrella-like body and then forcefully expel it backward. The resulting jet of water generates an equal and opposite momentum, pushing the jellyfish forward.

Squids use a similar jet propulsion strategy but with greater directional control. They can reorient their nozzles to steer in different directions, allowing more sophisticated navigation. These strategies are elegant biological examples of Newton’s third law and the conservation of momentum in fluid systems. Squids can reach speeds of 8 to 12 km/h using this propulsion method.

Medical Applications: The Ballistocardiograph

Conservation of momentum also appears in human physiology. Each time the heart pumps blood into the aorta, a force is exerted on the blood. According to Newton’s third law, an equal and opposite force is exerted on the body. This tiny movement was once measured using a device called a ballistocardiograph (BCG).

The BCG measured the recoil of the body in response to the heartbeat. By analyzing this motion, doctors could estimate the strength of the heart and the volume of blood being pumped. Although largely replaced by more advanced technologies like the electrocardiogram (ECG) and echocardiogram (ECHO), the BCG illustrates how physiological processes adhere to physical principles such as momentum conservation.

Making Connections: Conservation of Momentum and Collisions

Collisions provide one of the clearest demonstrations of momentum conservation. Whether in macroscopic systems like vehicles or in atomic-scale experiments, momentum before and after the collision remains constant, assuming no net external forces act.

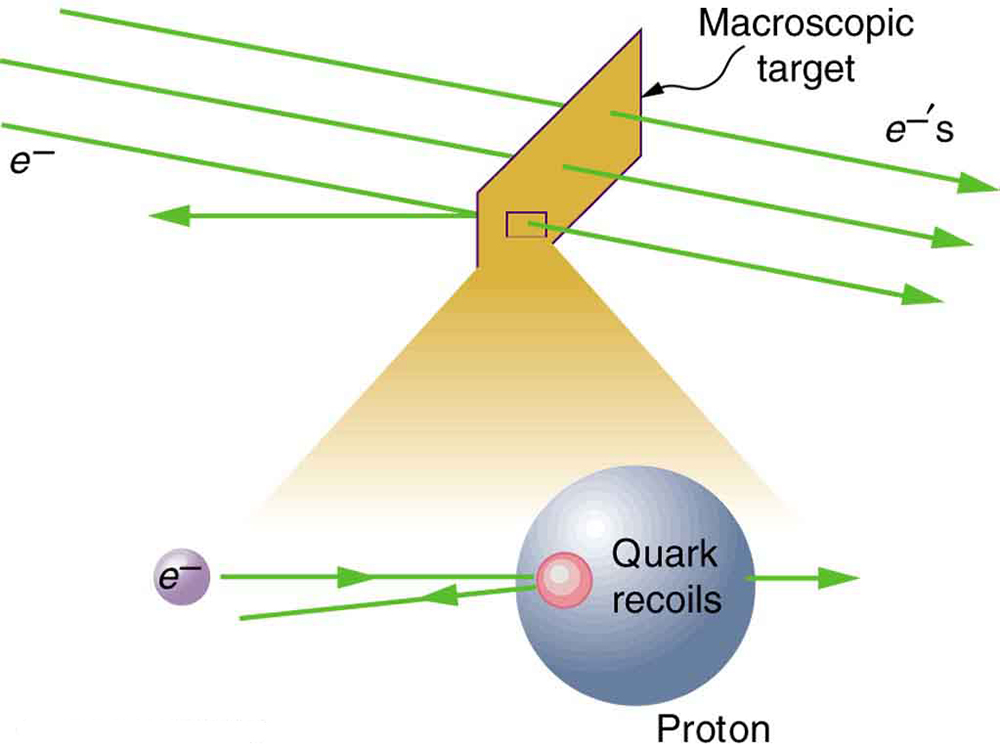
In particle physics, this principle is used to study the structure and behavior of subatomic particles. High-speed particles are collided in accelerators, and the outcomes are analyzed using conservation laws. For instance, the detection of quarks—the fundamental constituents of protons and neutrons—was made possible by analyzing backward-scattered electrons, a result explained by conservation of momentum during the collision.

Subatomic Collisions and Conservation

Momentum conservation is essential in the study of atomic and subatomic particles. In high-energy particle physics, conservation of momentum allows scientists to infer the existence of unseen particles. For example, when electrons are scattered off protons, the angles and velocities of the resulting particles can reveal the internal structure of the proton, including evidence for quarks (Figure 54.3).

An electron strikes on a macroscopic target and recoils back. A closer look shows the electron to scatter backward after interacting with the proton.
Figure 54.3: A subatomic particle scatters straight backward from a target particle. In experiments seeking evidence for quarks, electrons were observed to occasionally scatter straight backward from a proton.

Section Summary

  • The principle of conservation of momentum states that in an isolated system, the total momentum remains constant.
  • In symbolic form:
    [latex]\mathbf{p}_{\text{tot}} = \mathbf{p}'_{\text{tot}}[/latex]
  • An isolated system is one for which [latex]\mathbf{F}_{\text{net}} = 0[/latex].
  • Momentum conservation applies independently along the [latex]x[/latex]-, [latex]y[/latex]-, and [latex]z[/latex]-directions.
  • This principle is valid for both macroscopic and subatomic systems and is widely used in both engineering and biomedical applications.

Conceptual Questions

  1. Professional Application If you dive into water, you reach greater depths than if you do a belly flop. Explain this difference in depth using the concept of conservation of energy. Explain this difference in depth using what you have learned in this chapter.
  2. Under what circumstances is momentum conserved?
  3. Can momentum be conserved for a system if there are external forces acting on the system? If so, under what conditions? If not, why not?
  4. Momentum for a system can be conserved in one direction while not being conserved in another. What is the angle between the directions? Give an example.
  5. Professional Application Explain in terms of momentum and Newton’s laws how a car’s air resistance is due in part to the fact that it pushes air in its direction of motion.
  6. Can objects in a system have momentum while the momentum of the system is zero? Explain your answer.
  7. Must the total energy of a system be conserved whenever its momentum is conserved? Explain why or why not.

Problems & Exercises

  1. Professional Application Train cars are coupled together by being bumped into one another. Suppose two loaded train cars are moving toward one another, the first having a mass of 150,000 kg and a velocity of 0.300 m/s, and the second having a mass of 110,000 kg and a velocity of [latex]-0\text{.}\text{120 m/s}[/latex]. (The minus indicates direction of motion.) What is their final velocity?
  2. Suppose a clay model of a koala bear has a mass of 0.200 kg and slides on ice at a speed of 0.750 m/s. It runs into another clay model, which is initially motionless and has a mass of 0.350 kg. Both being soft clay, they naturally stick together. What is their final velocity
  3. Professional Application Consider the following question: A car moving at 10 m/s crashes into a tree and stops in 0.26 s. Calculate the force the seatbelt exerts on a passenger in the car to bring him to a halt. The mass of the passenger is 70 kg. Would the answer to this question be different if the car with the 70-kg passenger had collided with a car that has a mass equal to and is traveling in the opposite direction and at the same speed? Explain your answer.
  4. In a collision with an identical car, momentum is conserved. Afterwards [latex]{v}_{\text{f}}=0[/latex] for both cars. The change in momentum will be the same as in the crash with the tree. However, the force on the body is not determined since the time is not known. A padded stop will reduce injurious force on body.
  5. What is the velocity of a 900-kg car initially moving at 30.0 m/s, just after it hits a 150-kg deer initially running at 12.0 m/s in the same direction? Assume the deer remains on the car.
  6. A 1.80-kg falcon catches a 0.650-kg dove from behind in midair. What is their velocity after impact if the falcon’s velocity is initially 28.0 m/s and the dove’s velocity is 7.00 m/s in the same direction?

Glossary

conservation of momentum principle
when the net external force is zero, the total momentum of the system is conserved or constant
isolated system
a system in which the net external force is zero
quark
fundamental constituent of matter and an elementary particle
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book